285(1)表示一组数据分布的量

28.3 表示一组数据平均水平的量 【平均数】 1、概念与公式

把n个数的总和除以n，所得的商数x，叫做这n个数的平均数。 设一组数据中n个数：)(1321n321nxxxxnxxxxx，则，，，

平均数反映了这组数据的平均水平

例1、一组数据：451、449、453、452、454、447，求平均数 解一：x＝451+449+453+452+454+4476＝451 解二：（分析：可以认为，这组数据都在450上下浮动） x＝（1－1＋3＋2＋4－3）/6＝1 ∴x＝450＋1＝451

2、当一组数据，，，，n321xxxx的各个数据都在某一个常数a左右波动时，我们可以把这组数据写成，，，，axxaxxaxxaxxnn''33'22'11,

则有axaxxxxnxn')(1''3'2'

1

3、加权平均数 引例：某校初三4个班一次考试平均分为82、79、80、78分，4个班的人数分别是46、48、54、52人，求这个年级的平均分。

解：x＝(82×46+79×48+80×54+78×52)÷(46+48+54+52)＝79.7 加权平均数：kkkffffxfxfxx212211

＝1212121212kkkkkfffxxxfffffffff ＝1122kkmxmxmx 其中，m1,m2,…,mk叫做权，它们体现了x1,x2,…,xk对平均数x所产生的不同影响 例：某学生期中考试成绩60分，平时成绩70分（满分100分），按平时：期中：期末＝3：3：4的比重来划分，问该生在期末考试之后是否有可能学期总分达到80分？为什么？ 解：设期末考x分

100441080104370360xx

4、截尾平均数 在一些比赛中，如体操、跳水，均采用截尾平均数（即去掉一个最高分和一个最低分） 例、某运动员在体操比赛中8个裁判给出如下分数： 9.8、9.8、9.6、9.7、9.7、9.5、9.8、9.7，求出此人比较合理的最后得分。 x＝（9.8＋9.6＋9.7＋9.7＋9.8＋9.7）/6＝58.3/6＝9.717

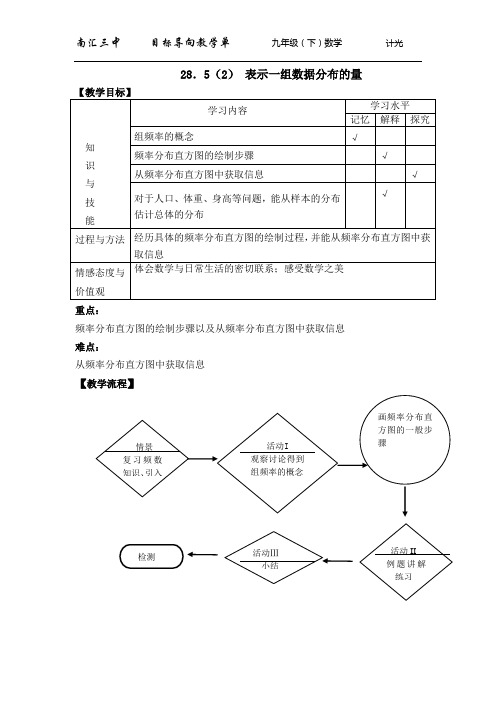
28．5（2） 表示一组数据分布的量重点：频率分布直方图的绘制步骤以及从频率分布直方图中获取信息 难点：从频率分布直方图中获取信息【教学流程】【学习导航】一、学习准备：1.为统计八年级某班全体学生英语学科期末考试成绩,制作了如下频数分布表(1)请完成这个频数分布表. (2)数据分组时的组距为__________,最大值和最小值的差最多为_______.(3)从频数分布表中可获得那些信息?(4)80分(包括80)以上人数占全班人数的百分比是____________ 二、新课探索：1、如下图，分别是A 班、B 班学生参加环保知识竞赛的成绩的频数分布直方图，根据图中信息该如何比较A 、B 两班参赛学生成绩的分布情况？A 学生有_____人，B 班学生有_____人.直接从个小组的频数比较两班的参赛成绩的分布情况比较困难.如果将每小组的频数除以全班数据总的个数，就可以得到各小组数据频数与全组数据总个数的比值，我们把这个比值叫做_______.全组数据的总个数小组中数据的频数组频率由于组频率表示比值大小,因此可以用组频率来比较两个人数______的两个班级学生成绩的分布情况.将频数分布表扩充到频率分布表:从频率分布表可比较A、B两班参赛学生成绩的分布情况.2.各小组的频率和为_____.3.如何画频率分布直方图?为了解学生用于阅读课外书籍的时间的情况，某校对九年级（1）班40名学生每周阅读课外书籍所用的时间进行统计.调查结果如下（时间单位：小时）：1.5, 3.5 ,9.0 ,5.0 ,4.5, 3.0 ,6.0,2.5 ,5.5 ,5.5 ,4.0, 3.0, 2.0, 6.5, 8.0, 2.5, 8.5, 7.0, 6.5, 4.0,9.5, 1.0, 4.0, 3.5, 7.5, 7.0, 1.0, 6.0, 0.0, 5.0,2.0, 5.5, 8.5, 6.0, 4.5, 4.0, 7.0, 6.0, 5.5, 9.0.填写频率分布直方图:在频率分布直方图中,用每小组的小矩形的面积表示该小组的组频率.频率纵轴表示:组距横轴:与频数分布直方图相同.组距频率________________________________每个小长方形的面积=_________________ 所有小长方形的面积和=____________4.对于人口、身高、体重等问题，我们可以通过大容量的随机样本的分布来推断总体的分布.例.为了了解全区6000名初中毕业生的体重情况,随机抽测了400名学生的体重,统计结果列表如下:(1)计算组频率,填入表内.(2)画出样本的频率分布直方图.(3)估计全区初中毕业生中体重小于60千克且不小于50千克的学生有_________人.三、课内小结：1. ______________________________________________叫做组频率.2. 频率分布直方图的横轴是指________________________________________;纵轴是指________________________________________________________. 3.各小矩形的面积为该小组的__________;各小矩形的面积和等于___________.【课内检测】1. 某中学数学教研组有25名教师,将他们按年龄分成三个小组,在38-45(岁)小组内有8名教师,那么这个小组的组频率是____________.2. 填写频率分布表中为完成部分. 思考:根据已知数据可先求什么?3.某商店上个月第一周五种不同品牌牙膏的售出量的频数分布如下：1)品牌A牙膏的频数是________，它的实际意义是_______________________2)品牌D牙膏的频率是________，它的实际意义是_______________________4.将学习导航1中A、B两班学生参加环保知识竞赛的成绩情况，编制频率分布表，画出相应频率分布直方图，并分析两班成绩的特征.。

《抽样技术》练习题5及答案习题⼀1.请列举⼀些你所了解的以及被接受的抽样调查。

2.抽样调查基础理论及其意义；3.抽样调查的特点。

4.样本可能数⽬及其意义；5.影响抽样误差的因素；6.某个总体抽取⼀个n=50的独⽴同分布样本，样本数据如下：567 601 665 732 366 937 462 619 279 287690 520 502 312 452 562 557 574 350 875834 203 593 980 172 287 753 259 276 876692 371 887 641 399 442 927 442 918 11178 416 405 210 58 797 746 153 644 4761）计算样本均值y与样本⽅差s2;2）若⽤y估计总体均值，按数理统计结果，ｙ是否⽆偏，并写出它的⽅差表达式；3）根据上述样本数据，如何估计v(y)？4）假定y的分布是近似正态的，试分别给出总体均值µ的置信度为80％，90％，95％，99％的（近似）置信区间。

习题⼆⼀判断题1 普查是对总体的所有单元进⾏调查，⽽抽样调查仅对总体的部分单元进⾏调查。

2 概率抽样就是随机抽样，即要求按⼀定的概率以随机原则抽取样本，同时每个单元被抽中的概率是可以计算出来的。

3 抽样单元与总体单元是⼀致的。

4 偏倚是由于系统性因素产⽣的。

5 在没有偏倚的情况下，⽤样本统计量对⽬标量进⾏估计，要求估计量的⽅差越⼩越好。

6 偏倚与抽样误差⼀样都是由于抽样的随机性产⽣的。

7 偏倚与抽样误差⼀样都随样本量的增⼤⽽减⼩。

8 抽样单元是构成抽样框的基本要素，抽样单元只包含⼀个个体。

9 抽样单元可以分级，但在抽样调查中却没有与之相对应的不同级的抽样框。

10 总体⽬标量与样本统计量有不同的意义，但样本统计量它是样本的函数，是随机变量。

11 ⼀个抽样设计⽅案⽐另⼀个抽样设计⽅案好，是因为它的估计量⽅差⼩。

12 抽样误差在概率抽样中可以对其进⾏计量并加以控制，随着样本量的增⼤抽样误差会越来越⼩，随着n越来越接近N，抽样误差⼏乎可以消除。

28.3 表示一组数据平均水平的量（1)——平均数与加权平均数［学习目标］1．理解一组数据的平均数、加权平均数的概念，知道“权"的含义; 2．会计算一组数据的平均数和加权平均数；3．理解样本平均数和总体平均数的意义，会根据随机样本的平均数估计总体样本平均数.[学习重难点］会求平均数、加权平均数；能用于解决简单的统计问题。

一、课前预习 问题：我国运动员刘翔在雅典奥运会获得男子110米栏项目的金牌.他在2006年参加该项目的重大国际赛事取得的成绩分别是12.88秒（新世界纪录)、13。

15秒和12.91秒；古巴运动员罗伯斯在2006年的国际赛事中取得的成绩分别是13.04秒、13秒和13.08秒；前世界名将内赫米亚赫曾跑出过13。

16秒、13秒和12。

93秒的成绩，综合他们的三次成绩来看，谁跑得最快？分析:我们只要计算他们三人的平均成绩就可以了。

解：二、课堂学习1．平均数：一般地，如果一组数据n x x x ,,,21 ,它们的平均数记作x ,则121()n x x x x n=+++。

①注：平均数反映了这组数据的平均水平;若n 个数n x x x ,,,21 都在常数a 附近波动，那么a x x +=11',a x x +=22'，…,a x x n n +=',记)'''(121n x x x n x +++= ，可得平均数计算公式：'x x a =+②.把样本中所有个体的平均数称为样本平均数; 把总体中所有个体的平均数称为总体平均数。

［说明］随机样本的容量越大，样本平均数就越接近总体平均数，必要时，可以用样本平均数来估计总体平均数。

例1 为掌握某作物种子的发芽情况,可随机取出100粒种子,在适宜的温度下做发芽天数的试验，如果试验的结果如表所示，你能估计出该作物种子发芽的平均天数吗?分析15粒、45粒、35粒、5粒，将这100粒种子发芽天数的总和除以100。