统计学习题 第十三章 检验与方差分析
- 格式:doc
- 大小:228.50 KB
- 文档页数:11

(完整word版)方差分析习题与答案统计学方差分析练习题与答案一、单项选择题1.在方差分析中,()反映的是样本数据与其组平均值的差异A总离差B组间误差C抽样误差D组内误差2.是()A组内平方和B组间平方和C总离差平方和D因素B的离差平方和3.是()A组内平方和B组间平方和C总离差平方和D总方差4.单因素方差分析中,计算F统计量,其分子与分母的自由度各为()Ar,nBr-n,n-rCr-1.n-rDn-r,r-1二、多项选择题1.应用方差分析的前提条件是()A各个总体报从正态分布B各个总体均值相等C各个总体具有相同的方差D各个总体均值不等E各个总体相互独立2.若检验统计量F=近似等于1,说明()A组间方差中不包含系统因素的影响B组内方差中不包含系统因素的影响C组间方差中包含系统因素的影响D方差分析中应拒绝原假设E方差分析中应接受原假设3.对于单因素方差分析的组内误差,下面哪种说法是对的?()A其自由度为r-1B反映的是随机因素的影响C反映的是随机因素和系统因素的影响D组内误差一定小于组间误差E其自由度为n-r4.为研究溶液温度对液体植物的影响,将水温控制在三个水平上,则称这种方差分析是()A单因素方差分析B双因素方差分析C三因素方差分析D单因素三水平方差分析E双因素三水平方差分析三、填空题1.方差分析的目的是检验因变量y与自变量某是否,而实现这个目的的手段是通过的比较。
2.总变差平方和、组间变差平方和、组内变差平方和三者之间的关系是。
3.方差分析中的因变量是,自变量可以是,也可以是。
4.方差分析是通过对组间均值变异的分析研究判断多个是否相等的一种统计方法。
5.在试验设计中,把要考虑的那些可以控制的条件称为,把因素变化的多个等级状态称为。
6.在单因子方差分析中,计算F统计量的分子是方差,分母是方差。
7.在单因子方差分析中,分子的自由度是,分母的自由度是。
四、计算题1.有三台机器生产规格相同的铝合金薄板,为检验三台机器生产薄板的厚度是否相同,随机从每台机器生产的薄板中各抽取了5个样品,测得结果如下:机器1:0.236,0.238,0.248,0.245,0.243机器2:0.257,0.253,0.255,0.254,0.261机器3:0.258,0.264,0.259,0.267,0.262问:三台机器生产薄板的厚度是否有显著差异?2.养鸡场要检验四种饲料配方对小鸡增重是否相同,用每一种饲料分别喂养了6只同一品种同时孵出的小鸡,共饲养了8周,每只鸡增重数据如下:(克)配方:370,420,450,490,500,450配方:490,380,400,390,500,410配方:330,340,400,380,470,360配方:410,480,400,420,380,410问:四种不同配方的饲料对小鸡增重是否相同?3.今有某种型号的电池三批,它们分别为一厂、二厂、三厂三个工厂所生产的。

第十三章实验设计一、教学大纲要求(一)掌握内容1. 实验设计的基本原则随机化原则、对照的原则(对照的类型,对照的设置)、重复的原则。
2. 实验设计的基本内容和步骤3. 常用的实验设计方法(1)随机化分组方法;(2)完全随机分组设计;(3)配对设计;(4)配伍组设计及随机分组方法。
4.确定样本含量确定样本含量应当具备的条件:α、1-β、δ、σ 。
(二) 熟悉内容1. 常用的估计样本含量的计算方法及估计该试验的检验效能的方法。
(1)两样本均数比较。
(2)配对试验。
(3)样本均数与总体均数的比较。
(4)两样本率的比较。
(5)配对资料进行卡方检验时的样本含量估计。
(6)抽样调查估计总体均数的样本含量。
(7)抽样调查估计总体率的样本含量。
2. 一致性检验:Kappa值的意义及计算。
(三)了解内容1 实验设计的特点和分类。
2.临床设计书的主要内容。
3.Kappa值的抽样误差和假设检验。
二、教学内容精要(一)实验设计的特点和分类实验研究(experimental study)是指研究者根据研究目的(或研究假设),主动加以干预措施,并观察总结其结果,回答假设研究所提出的问题的一种研究方法。
实验研究可根据研究对象的不同分为两类:以动物或标本为研究对象的实验研究(experiment)和以人为研究对象的临床试验(clinical trial)。
(二)实验设计的基本原则1.随机化原则总体中的每一个观察单位都有同等的机会被选入实验组和对照组或进入样本,保证了非处理因素在各组间均衡一致而使样本具有代表性。
2.对照原则正确的设立对照可可控制实验过程中非实验因素的影响和偏倚,从而使处理因素的效应充分的显露出来。
设立对照组的常见方法有:空白对照、安慰剂(placebo)对照、实验对照、标准对照及自身对照。
3.重复的原则保证每一个处理都有足够的重复数(样本量),避免把偶然性或巧合的现象当作必然的规律性现象,并能正确的估计实验误差。
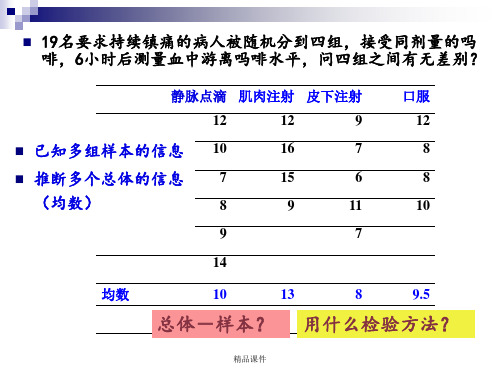

第十三章单因素设计方差分析方差分析是由英国统计学家Ronald Fisher 研究出来的,并以他的名字命名的方法,称为F检验。
它可以解决单因素和多因素实验设计结果的数据处理问题。
早期的心理学实验是严格的实验室控制实验。
在实验中只允许研究者感兴趣的一种变量作为自变量,希望观察到自变量引起的因变量的变化。
自变量也称为因素(factor),在实验中只安排一个自变量的实验叫做单因素实验。
经典心理学实验通常是单因素实验。
单因素的实验可以较明确的观察到自变量与因变量之间的因果关系,较适用于研究比较单纯的心理现象,但往往无法说明复杂的心理现象。
现代的实验设计将一些额外变量引入实验成为实验中新的因素,以期实验的结果更贴近真实的情景,从而发展了多因素的实验设计。
统计中用符号表示实验设计时,常用大写的英文字母表示因素,如因素A、因素B、因素C等;用S表示被试(subject)。
把S写在表示因素符号的后边、前面或中间,则表示不同的实验设计,例如:单因素被试间设计AS、单因素被试内设计SA、多因素被试间设计ABS、多因素被试内设计SAB、混合设计ASB。
第一节t检验与I类错误当两个总体没有差异,而统计推论的结论说有差异,就犯了I类错误;当两个总体存在差异,而统计推论的结论说没有差异,就犯了II类错误。
通常,I类错误的发生概率用α表示,II类错误发生的概率用β表示。
当采用多个两两t检验时,发生I类错误的概率就会增大。
I类错误的计算公式如下:I类错误发生的概率=1-(1-α)C(13.1)所以当要比较3个或3个以上的总体平均数两两检验时,应采用方差分析(analysis of variance)的方法。
一个显著的F值表示,在所比较的总体平均数里至少有两个总体平均数存在着显著差异。
第二节方差分析的原理方差(V ariance)有时也称为变异数(V ariation),是表示一组数据离散程度的统计量。
方差的总体参数用符号σ2表示;方差的样本统计量用符号S2表示。

医学统计学方差分析练习题1.两样本均数的比较,可用()。
A.方差分析B.t检验C.两者均可D.方差齐性检验2.随机区组设计的方差分析中,ν区组等于()。
A.ν总-ν误差B.ν总-ν处理C.ν总-ν处理+ν误差D.ν总-ν处理-ν误差4.方差分析中变量变换的目的是()。
A.方差齐性化B.曲线直线化C.变量正态化D.以上都对5.下面说法中不正确的是()。
A.方差分析可以用于两个样本均数的比较B.完全随机设计更适合实验对象变异不太大的资料C.在随机区组设计中,每一个区组内的例数都等于处理数D.在随机区组设计中,区组内及区组间的差异都是越小越好6.随机区组设计要求()。
A.区组内个体差异小,区组间差异大B.区组内没有个体差异,区组间差异大C.区组内个体差异大,区组间差异小D.区组内没有个体差异,区组间差异小7.完全随机设计方差分析的检验假设是()。
A.各对比组样本均数相等B.各对比组总体均数相等C.各对比组样本均数不相等D.各对比组总体均数不相等8.完全随机设计、随机区组设计的SS和及自由度各分解为几部分()。
A.2,2 B.2,3 C.2,4 D.3,39.配对t检验可用哪种设计类型的方差分析来替代()。
A.完全随机设计B.随机区组设计C.两种设计都可以D.AB都不行10、经方差分析,若P≤α,则结论为:()A、各样本均数全相等B、各样本均数不全相等C、至少有两个样本均数不等D、至少有两个总体均数不等E、各总体均数不等11、F检验不能用于()A.两样本方差的比较 B.回归系数的假设检验C. 两个样本频率的检验D、两个样本均数的比较E、多个样本均数的比较12、完全随机设计的方差分析中,组内变异反映的是()A、随机误差B、抽样误差C、测量误差D、个体差异E、系统误差13、某职业病防治院测定了11名石棉沉着病患者、9名石棉沉着病可疑患者和11名非患者的用力肺活量,求得其均数为1.79L,2.31L和3.08L,能否据此认定石棉沉着病患者、石棉沉着病可疑患者和非患者的用力肺活量不同?()A、能,因3个样本均数不同B、需作3个均数两两的t检验才能确定C、需用3个均数两两的SNK-q检验D、需作成组设计的3个均数比较的ANOV A14、完全随机设计方差分析中()A、组间SS不会小于组内SSB、组内SS不会小于组间SSC、组间MS不会小于组内MSD、F不可能是负数E、F可能是负数15、方差分析中,当P<0.05时,进一步作()A、t检验B、Z检验C、t’检验D、F检验E、q检验16、各组方差不齐时,可以作()A、近似检验B、秩和检验C、数据变换D、ABC都可以E、方差分析17、三组以上某实验室指标观测数据服从正态分布且满足参数检验的应用条件,任两组分别进行多次t检验代替方差分析,将会()A、明显增大犯第一类错误的概率B、使结论更具体C、明显增大犯第二类错误的概率D.使均数相差更显著E、使均数的代表性更好18、完全随机设计的方差分析中,组间均方主要反映()A、抽样误差大小B、n个数据的离散程度C、处理因素的作用D、随机误差的影响E、系统误差的影响19、多组均数的两两比较中,若用t检验,不用q检验,则()A、会将有差别的总体判断为无差别的概率增大B、会将无差别的总体判断为有差别的概率增大C、结果更合理D、结果会一致E、以上都不对20、对k个处理组,b个随机区组资料的方差分析,其误差的自由度为()A、kb-k-bB、kb-k-b-1C、kb-k-b-2D、kb-k-b+1E、kb-k-b+223、完成下列方差分析表变异来源SS DF MS F组间( ) 2 ( ) ( ) 组内( ) ( ) 0.0548总变异10.800 30计算分析题1.根据表1资料说明大白鼠感染脊髓灰质炎病毒后,再做伤寒或百日咳接种是否影响生存日数?若结论为“有影响”,请做多重比较(与对照组比)。

第十三章双变量关联性分析【思考与习题】一、思考题1.两变量间的关联性是否可解释为因果关系2.2⨯2列联表的关联性分析与两样本率比较的2χ检验有何不同3.相关系数r经假设检验有统计学意义,且得到的P值很小,是否表示两变量间一定有很强的直线关系4.简述Pearson积矩相关与Spearman秩相关的区别与联系。
二、案例辨析题为研究年龄与牙齿AKP酶反应活性之间的关系,某医生在其接诊的患者中随机抽取281例,按年龄(岁)分为三组进行观测,测量各患者牙齿的AKP酶反应活性,如表13-1所示。
问年龄与牙齿AKP酶反应活性之间有无关系表13-1 281例患者年龄与牙齿AKP酶反应活性的分布年龄AKP酶反应活性合计—+++<31517365831~234549051~249712133合计31148102 281按照R×C表的2χ检验结果,得2χ=,005.0<P,故按α=水准,拒绝H,可认为不同年龄患者的AKP酶反应活性不同,两者之间有关系。
以上分析正确吗三、最佳选择题1.Pearson积矩相关系数的假设检验,其自由度为A.1-nB.2-nC .12-nD .)1(2-nE .n2.积矩相关系数的计算公式是 A .xy xy yyl r l l =B.r =C.l r =D.l r =E.r =3. 直线相关分析中,若0.05,||r r ν>,则可认为两变量之间 A. 有一定关系B. 不存在直线相关关系C. 有直线相关关系D. 有直线相关关系,且为正相关E. 有直线相关关系,且为负相关 4.下列指标中可正可负的是 A .F 统计量 B .2χ统计量 C .21()nxx i l x x ==-∑D .1()()nxy i l x x y y ==--∑E .21()nyy i l y y ==-∑5.研究18岁女大学生体重和肺活量的关系时,表达正确的无效假设是 A .体重与肺活量无关联 B .体重与肺活量有关联 C .体重与肺活量有直线关系 D .体重与肺活量有因果关系 E .体重与肺活量无因果关系 6.计算Pearson 列联系数的公式为 A.l r =B .nr +=22χχC .22χχnr +=D .12-=n r χE .nr +=22χχ7.某放射科医师收集脑外伤患者30例,观察脑出血直径和病人昏迷的程度(轻度、中度、重度),欲分析昏迷程度是否与病灶大小有关,可进行 A .Pearson 相关分析 B .Spearman 秩相关分析 C .两小样本比较的t 检验 D .方差分析 E .2χ检验8.对两个分类变量的频数表资料作关联性分析,可用 A .积矩相关或等级相关B .积矩相关或列联系数C .列联系数或等级相关D .积矩相关E .等级相关9.两组数据分别进行直线相关分析,对1r 进行假设检验得到P <,对2r 进行假设检验,得到P <,可以认为A .第一组的两个变量关系比第二组密切B .第二组的两个变量关系比第一组密切C .更有理由认为第一组的两个变量之间有直线关系D .更有理由认为第二组的两个变量之间有直线关系E .两组变量关系同样密切四、综合分析题1.为研究某病成年男性患者血浆清蛋白含量与血红蛋白含量的关系,某医生测得10名患者血浆清蛋白含量(g/L)及血红蛋白含量(g/L)见表13-2所示,试分析二者是否有关联。
第一章绪论1.举例说明总体和样本的概念。
研究人员通常需要了解和研究某一类个体,这个类就是总体。
总体是根据研究目的所确定的所有同质观察单位某种观察值(即变量值)的集合,通常有无限总体和有限总体之分,前者指总体中的个体是无限的,如研究药物疗效,某病患者就是无限总体,后者指总体中的个体是有限的,它是指特定时间、空间中有限个研究个体。
但是,研究整个总体一般并不实际,通常能研究的只是它的一部分,这个部分就是样本。
例如在一项关于2007年西藏自治区正常成年男子的红细胞平均水平的调查研究中,该地2007年全部正常成年男子的红细胞数就构成一个总体,从此总体中随即抽取2000人,分别测的其红细胞数,组成样本,其样本含量为2000人。
2.简述误差的概念。
误差泛指实测值与真实值之差,一般分为随机误差和非随机误差。
随机误差是使重复观测获得的实际观测值往往无方向性地围绕着某一个数值左右波动的误差;非随机误差中最常见的为系统误差,系统误差也叫偏倚,是使实际观测值系统的偏离真实值的误差。
3.举例说明参数和统计量的概念。
某项研究通常想知道关于总体的某些数值特征,这些数值特征称为参数,如整个城市的高血压患病率。
根据样本算得的某些数值特征称为统计量,如根据几百人的抽样调查数据所算得的样本人群高血压患病。
统计量是研究人员能够知道的,而参数是他们想知道的。
一般情况下,这些参数是难以测定的,仅能够根据样本估计。
显然,只有当样本代表了总体时,根据样本统计量估计的总体参数才是合理的。
4.简述小概率事件原理。
当某事件发生的概率小于或等于0.05时,统计学上习惯称该事件为小概率事件,其含义是该事件发生的可能性很小,进而认为它在一次抽样中不可能发生,这就是所谓的小概率事件原理,它是进行统计推断的重要基础。
第二章调查研究设计1.调查研究主要特点是什么?调查研究的主要特点是:①研究的对象及其相关因素(包括研究因素和非研究因素)是客观存在的,不能人为给予干预措施②不能用随机化分组来平衡混杂因素对调查结果的影响。
方差分析习题及答案方差分析习题及答案方差分析是一种统计方法,用于比较两个或多个样本均值之间的差异。
它可以帮助我们确定是否存在显著的差异,并进一步了解这些差异的来源。
在本文中,我们将介绍一些方差分析的习题,并提供相应的答案。
习题一:某研究人员想要比较三种不同的肥料对植物生长的影响。
他随机选择了30个植物,并将它们分成三组,每组10个。
每组植物分别使用不同的肥料进行施肥。
研究人员在10天后测量了每组植物的平均生长高度(单位:厘米)。
下面是测量结果:组1:12, 14, 15, 16, 17, 13, 14, 15, 16, 18组2:10, 11, 13, 12, 14, 15, 13, 12, 11, 10组3:9, 10, 8, 11, 12, 13, 10, 9, 11, 12请使用方差分析方法,判断这三种肥料是否对植物生长有显著影响。
答案:首先,我们需要计算每组的平均值和总体平均值。
组1的平均值为15.0,组2的平均值为11.1,组3的平均值为10.5。
总体平均值为12.2。
接下来,我们计算组内平方和(SS_within),组间平方和(SS_between)和总体平方和(SS_total)。
根据公式,我们有:SS_within = Σ(xi - x̄i)^2SS_between = Σ(ni * (x̄i - x̄)^2)SS_total = Σ(xi - x̄)^2其中,xi代表第i组的观测值,x̄i代表第i组的平均值,x̄代表总体平均值,ni代表第i组的样本量。
计算得到:SS_within = 23.0SS_between = 48.6SS_total = 71.6接下来,我们计算均方(mean square):MS_within = SS_within / (n - k)MS_between = SS_between / (k - 1)其中,n代表总样本量,k代表组数。
计算得到:MS_within = 2.56MS_between = 24.3最后,我们计算F值:F = MS_between / MS_within计算得到:F = 9.49根据F分布表,自由度为2和27时,F临界值为3.35。
统计学方差分析练习题与答案一、单项选择题1.在方差分析中,()反映地是样本数据与其组平均值地差异A 总离差B 组间误差C 抽样误差D 组内误差2.是()A 组内平方和B 组间平方和C 总离差平方和D 因素B地离差平方和3.是()A 组内平方和B 组间平方和C 总离差平方和D 总方差4A r,1AD2ACE3ACE4(AD12345.在试验设计中,把要考虑地那些可以控制地条件称为,把因素变化地多个等级状态称为 .6.在单因子方差分析中,计算F统计量地分子是方差,分母是方差.7.在单因子方差分析中,分子地自由度是,分母地自由度是 .四、计算题1.有三台机器生产规格相同地铝合金薄板,为检验三台机器生产薄板地厚度是否相同,随机从每台机器生产地薄板中各抽取了5个样品,测得结果如下:机器1:0.236,0.238,0.248,0.245,0.243机器2:0.257,0.253,0.255,0.254,0.261机器3:0.258,0.264,0.259,0.267,0.262问:三台机器生产薄板地厚度是否有显著差异?2.养鸡场要检验四种饲料配方对小鸡增重是否相同,用每一种饲料分别喂养了6只同一品种同时孵出地小鸡,共饲养了8周,每只鸡增重数据如下:(克)配方:370,420,450,490,500,450配方:490,380,400,390,500,410配方:330,340,400,380,470,360配方:410,480,400,420,380,410问:四种不同配方地饲料对小鸡增重是否相同?3.今有某种型号地电池三批,它们分别为一厂、二厂、三厂三个工厂所生产地.为评比其一厂二厂三厂41.1.1234567.四、计算题1.解:根据计算结果列出方差分析表因为(2,12)=3.89<32.92,故拒绝,认为各台机器生产地薄板厚度有显著差异.2.解:根据计算结果列出方差分析表。
第十三章2χ检验与方差分析第一节拟合优度检验拟合优度检验(比率拟合检验)·正态拟合检验第二节无关联性检验独立性、理论频数及自由度·频数比较和连续性修正·关系强度的量度第三节方差分析总变差及其分解·自由度·检验统计量F o的计算·相关比率·方差分析的几点讨论第四节回归方程与相关系数的检验回归系数的检验·积差系数的检验·回归方程的区间估计一、填空1.方差分析可以对多个总体()是否相等进行检验。
2.列联表是按()标志把两个变量的频数进行交互分类的。
χ检验法进行列联表检验所使用的自由度为( )。
3.在使用24.在对( ) 的列联表进行检验时,存在着)1(2αχ=2αZ的关系。
5.列联表检验是通过()而不是通过相对频数的比较进行的。
6.方差分析是()检验的推广,一般用于处理自变量是一个(或多个)定类变量和因变量是一个定距变量之间的关系。
7.在对6×5的列联表进行方差分析时,与组间平方和相联系的自由度为(),与组内平方和相联系的自由度为(),与总平方和相联系的自由度为()。
8.方差分析中把已解释的变差对总变差的比值称为()。
9.检验两个总体变量(定距—定距变量)是否具有线性关系,主要是检验总体的()是否等于零。
10.对于定距—定距变量计算积差系数r时,要求相关的两个变量均为()变量。
在回归分析中,只有()变量才是随机的。
11.在实际运用中,方差分析的结果常用一种称为()的标准形式的表格表示出来。
Y±1S Y/X ,那么在散点图上约有()%的观测点落在其间。
12.取cY±2S Y/X ,那么在散点图上约有()%的观测点落在其间13.取cY±3S Y/X ,那么在散点图上约有()%的观测点落在其间。
14.取c二、单项选择1.在2χ比率拟合优度检验中,对于选定的显著性水平α求临界值2αχ,此时的自由度是( )。
A 实验数据总数n ―1B 变量X 的取值种类数c ―lC 实验数据总数n — 变量X 的取值种类数cD 实验数据总数n + 变量X 的取值种类数c2.在2χ正态拟合优度检验中,对于选定的显著性水平α求临界值2αχ,此时的自由度是( )。
A 数据的分组数B 数据的分组数―lC 数据的分组数―2D 数据的分组数―33.使用2χ检验法对n ×c 列联表进行无关联性检验,与2o χ这个检验统计量相联系的自由度( )。
A n ―1B c ―lC n ―cD (n —1)×(c —1)4.对于一个复杂的列联表,还可以把它进一步分解为许多子表,以确定表格的那一部分卡方2o χ影响最大。
这是利用了卡方分布的( )。
A 恒正性B 方差为期望值的2倍C 可加性D 前三者5.在方差分析中,自变量是( )。
A 定类变量B 定序变量C 定距变量D 定比变量 6.在直线回归分析中,相关比率PRC=0.750。
那么,积差系数r=( )。
A 0.750B 0.5625C 1.333D 0.866三、多项选择1.可以用于拟和优度检验的方法有( )。
A2χ检验 B F 检验C 累计频数检验D 游程检验 2.方差分析法( )。
A 可以用于一个总体均值是否相等的检验B 可以用于两个总体均值是否相等的检验C 可以用于三个总体均值是否相等的检验D 可以用于多个总体均值是否相等的检验3.对拟和优度推断结果,下列说法正确的是( )。
A 当试验规模很小而作出维持原假设决定时,这可能只是数据太少,不是真的表明实际情况切合零假设B 数据少如果否定了零假设,这一否定的可靠性是很大的C 规模极大的试验可把零假设有极细微的差别检测出来,而这种差别可能并无多大实际意义D 若试验规模很大而仍能维持原假设,则可视为是对原假设的有力支持4.使用2χ检验拟和优度,下列说法正确的是( )。
A 相对频数相同的列联表,在统计检验中其显著性相同B 相对频数相同的列联表,在统计检验中其显著性并不相同χ不变C 相对频数相同的列联表,样本容量增加K倍,2oχ变也扩大K倍D 相对频数相同的列联表,样本容量增加K倍,2o5.相关比率PRE度量的可以是()A 定类—定距变量之间的相关程度B 定距—定距变量之间的相关程度C 线性相关D 非线性相关6.下列说法正确的是()。
A 方差分析的优点在于,一个检验可以代替多个均值差检验B 方差分析总是优于一系列的均值差检验C方差分析中的自变量X如果是二分变量,不论采用方差分析或均值差检验,其结果完全相同D总变差分解的思想可以直接推广至多因素显著性检验7.方差分析所包含的假定包括()。
A 正态分布B 独立随机样本C 等方差性D 非负性四、名词解释1.拟和优度检验2.列联表3.理论频数4.方差分析5.方差分析表6.总变差7.组内变差8.组间平方和9.相关比率10.估计标准误差五、判断题1.理论频数f e与观测频数f o越接近,经验分布与理论分布拟合程度越好。
()2.对于拟合优度检验,在试验规模大时,否定零假设的意义大,接受零假设的意义不大。
()3.规模极大的试验可把零假设有极细微的差别检测出来。
()4.如何求得列联表中的理论频数就成了独立性检验的关键。
()χ检验法用于对交互分类资料的独立性检验,有其它方法无法比拟的优点。
5.2()χ检验不适用于定类变量和定序变量的相关统计。
()6.27.在2×2列联表中,若不能从卡方表中准确得到所需要的临界值,可以取事先未预测χ的近似值。
()方向的 (Zα/2)2来找出2α8.相对频数相同的列联表,在统计检验中其显著性也相同。
()9.组内变差反映了数据的c个“中心”的散布程度。
()10.组间平方和反映了数据围绕各“中心”的散布程度。
()11.方差分析是用(可以解释的方差)/(不能解释的方差)作为检验统计量。
()12.我们不可以从总平方和减去组间平方和来求组内平方和。
()η只可用于一个定类变量与一个定距变量的相关程度的测定。
()13.214.方差分析的优点在于,一个检验可以代替多个检验。
()15.如果仔细运用均值差检验,它可能会提供比方差分析更多的信息。
()16.拟合值Y c上下设置一个合适区间,那么Y被估计到的可能性便会大大增加。
()六、计算题1.一位社会学家想知道私立本科大学每年的生源是否呈均匀分布。
为此,他在某校随机抽取了4500个本科生,这些学生的分布是:一年级1200人,二年级1100人,三年级1150人,四年级1050人。
试问,在给定显著性水平α为0.05下,四个年级学生人数构成是否均匀?2 .一位遗传学家想知道某种紫花的颜色是否符合孟德尔隐性遗传规律,按照这种规律两种粉色杂交后,后代将以白∶粉∶红=1∶2∶1的比例出现。
他做了一项杂交实验,植株了100株后代,结果发现:21株白,61株粉,18株红。
试问,在给定显著性水平α为0.05下,是否植株后代以白:粉:红=1∶2∶1的比例出现?3.某种动物的两个品种杂交后可能出现四种特征。
某种理论分析表明,可能出现的四种特征的数量将以9∶3∶3∶1的比例出现。
生物学家为此做了一项实验,检查了160个后代,结果发现具有着四种特征的后代的数量分别是72、38、32、18。
试问,在给定显著性水平α为0.05下,是否杂交后代以9∶3∶3∶1的比例出现?4.某公司对电视机的可靠性进行了一次调查,使用100台电视机作样本,记录了在电视机出现故障之前所经历的月份。
根据经历的月份(按等级划分),下表给出了出现故障的要求:检验故障的实际分布与正态分布是否有明显差别(α取0.05)。
取0.05)。
试问,居民对生活质量的要求与年龄是否有明显的关系(α试问,子辈职业与父辈职业之间是否存在相关关系?(α取0.05)8.某中学想知道城市学生家长和农村学生家长对延长学生在校时间是否持不同看法。
研究者随机抽出来自农村和城市的两个家长样本,调查结果表明:在来自城市的200位家长中, 123人支持,36人反对,41人没有看法;在来自农村的300位家长中, 145人支持,85人反对,70人没有看法。
试问,家长对学生延长在校时间的看法是否与其居住在城市或农村有关?(α取0.01)9.某连锁商业企业在同城三个不同地点开设了三个分店,从这三家商店随机抽出5天的营业额的数据如下表所示:要求:(1)求三家店每天的平均每天的营业额和5天的平均每天营业额;(2)求总变差、组内变差和组间平方和;(3)编制方差分析表;(4)检验三个商店的地点不同对每天的营业额是否有显著的影响(5) 计算商店的地点不同对每天的营业额之间的相关比率。
10.为了研究职业与家庭子女数之间的关系,随机地抽出了41户家庭进行了调查,调查三种职业家庭的子女数的资料如下:工人:1,3,4,4,6,2,3,4,3,5,2,4;干部:3,5,0,5,4,4,2,3,1,3,2,3,3,2,4,2,6,1;知识分子:6,4,2,2,3,0,5,3,1,2,1。
要求:(1)求三种职业家庭户均子女数;(2)求总变差、组内变差和组间平方和;(3)编制方差分析表;(4)检验不同职业的生育观是否有显著的不同。
(5)计算职业与子女数量之间的相关比率。
11.有关雇员初始年薪和他10年后的年薪之间的一项调查,共抽取了13名雇员。
数据表明,二者之间的积差系数是0.570。
现给定α=0.05,试检验此相关系数是否显著。
12.1992—2003年我国城镇居民人均消费性支出和人均可支配收入的数据见下表:要求:(1)计算我国城镇居民人均消费性支出和人均可支配收入的积差系数;(2)检验所计算的积差系数的显著性;(3)建立我国居民人均消费支出依人均可支配收入的线性回归模型;(4)计算居民人均消费支出与人均可支配收入之间的相关比率,说明这一相关比率与积差系数的数量关系;(5)计算估计标准误差;(6)已知某年我国居民人均年可支配收入为8000元,试以95%的置信度预测人均年消费性支出的估计区间。
13.某银行25家分行的不良贷款额与贷款余额调查数据如下(单位:亿元):要求:(1)计算各项贷款余额和不良贷款额的积差系数;(2)检验所计算的积差系数的显著性;(3)建立不良贷款额依各项贷款余额的线性回归模型;(4)对回归模型进行F检验;(5)计算估计标准误差;(6)求出贷款余额为100亿元时,不良贷款95%的置信区间.七、问答题1.对于拟合优度检验,解释统计推断的结果时,应注意些什么?、积差系数之平方r2和相关指数R之间的关系。
2.简述相关比率2参考答案一、填空1.均值 2.品质 3.=df (c -1)(r -1) 4.2×2 5.频数 6.均值差 7. 4,1,5 8.相关比率 9.回归系数B 10.随机,因 11.方差分析表 12.68.26 13.95.46 14.99.73二、单项选择1.B 2.D 3.D 4.C 5.A 6.D三、多项选择1.AC 2.BCD 3.ABCD 4.BD 5.ABCD 6.ACD 7.ABC四、名词解释1.拟和优度检验:是有关检定总体是否具有正态或其他分布形式的非参数统计检验。