- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由度为 k-r-1=7。由
22.15 2 k2r1( ) 18.48.
于是,拒绝原假设,即认为棉纱拉力强
度不服从正态分布。
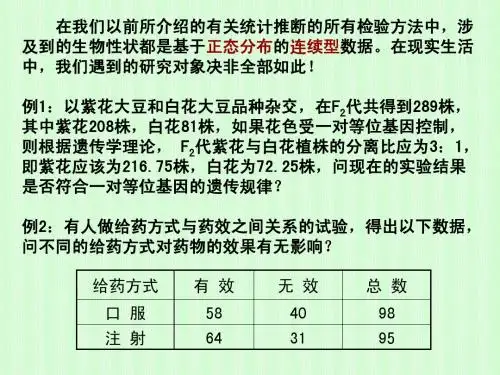
χ 2检验的一个著名应用例子是孟德尔豌豆 实验。奥地利生物学家孟德尔在1865年发表的 论文,事实上提出了基因学说,奠定了现代遗 传学的基础。他的这项伟大发现的过程有力地 证明了统计方法在科学研究中的作用。因此, 我们有必要在这里将这一情况介绍给大家。
§8.4 拟合优度检验
在前面的讨论中,我们总假定总体的分 布形式是已知的。例如,假设总体分布为正
态分布 N(, 2), 总体分布为区间 (a, b) 上的
均匀分布,等等。
然而,在实际问题中,我们所遇到的总 体服从何种分布往往并不知道。需要我们先 对总体的分布形式提出假设,如:总体分布
是正态分布N( , 2),总体分布是区间(a, b)
上均匀分布等,然后利用数据 (样本) 对这一 假设进行检验,看能否获得通过。
解决这类问题的方法最早由英国统计学 家K. Pearson (皮尔逊) 于1900年在他发表的 一篇文章中给出, 该方法后被称为Pearson χ 2 检验法,简称χ 2检验。
这是一项非常重要的工作, 许多学者视它为近代统计学的 开端。
设F(x)为一已知的分布函数,现有样本 X1, X2, …, Xn,但我们并不知道样本的总体分 布是什么。现在试图检验
H0:总体X的分布函数为F(x) ; (1)
对立假设为H1:总体 X 的分布函数非F(x)。 如果F(x)形式已知,但含有未知参数θ 或参
数向量θ =(θ1, θ2,…, θr ) ,则记其为F(x,θ )。
(3). 计算各子区间 Ii 上的实际频数 fi 。
fi =﹟{ X1, X2, …, Xn ∈ Ii } , i=1, 2, …, k .
计数符号,取集 合中的偏差平方和。
2
k
[
i1
fi
npi (ˆ)]2 npi (ˆ)
,
( 2)
每一项用npi (ˆ) 去除的其目的是:缩小理论
μˆ X 1.41, σˆ2 n 1 S 2 0.262. n
(1). 先将数据Xi 分成13组,每组落入一个区 间,区间的端点为:a0 , a1 0.64,
a2 0.78, ,a12 2.18,a13 .
(2). 计算数据落入各子区间的理论频数。
因分布中含有两个未知参数,所以,理论
在实用上,一般要求n ≥ 50,以及所有
npi ≥5。如果初始子区间划分不满足后一个 条件, 则适当地将某些子区间合并,可使npi 满足上述要求。
例1:为检验棉纱的拉力强度X(单位: 千克) 服 从正态分布,从一批棉纱中随机抽取300条进 行拉力试验,结果列在表8.2中。给定α= 0.01, 检验假设
频数只能近似地估计。落入第 i 个子区间Ii 的理论频数的估计为 npˆi , 其中
pˆ i
pˆi (ˆ,ˆ
2)
ai 1.41 0.26
ai1 1.41, 0.26
i 1,2, ,13.
因 npˆ1 0.46,npˆ2 1.85,npˆ12 1.85,npˆ13 0.46, 而 npˆ3, ,npˆ11 均大于5,所以,我们将前两组和
孟德尔在关于遗传问题的研 究中,用豌豆做实验。豌豆有黄 和绿两种颜色,在对它们进行两 代杂交之后,发现一部分杂交豌 豆呈黄色,另一部分呈绿色。其 数目的比例大致是 3:1。
孟德尔把他的实验重复了多次,每次都 得到类似结果。
这只是一个表面上的统计规律。但它启 发孟德尔去发展一种理论,以解释这种现象。 他大胆地假定存在一种实体,即现在我们称 为“基因”的东西,决定了豌豆的颜色。这 基因有黄绿两个状态,一共有四种组合:
(2). 计算各子区间 Ii 上的理论频数。
如果总体的分布函数为F(x,θ ),那么每个
点落在区间 Ii 上的概率均为
pi ( ) F(ai , ) F(ai1, ), i 1,2, ,k.
n个点中,理论上有npi (θ )个点落在 Ii 上, (称为理论频数)。当分布函数中含有未知
参数θ 时,理论频数也未知,要用 npi (ˆ) 来估计npi (θ ),其中 ˆ 为θ 的极大似然估。
频数比较大的那些项在和式中的影响力。
可以证明:在 H0 成立,且n→∞时,
2
2 k -r-1
,
( 3)
即 2统计量的分布收敛到自由度为k r 1
的 2分布,k是子区间数,r是参数个数。
(5). H0的显著性水平为α的检验的拒绝域为
2 k2-r-1 ( ),
( 4)
注意:该检验方法是在 n 充分大时使用 的,因而,使用时要注意 n必须足够地大, 以及 npi 不能太小这两个条件。
这种检验通常称为拟合优度检验。
不妨设总体 X 是连续型分布。检验思想 与步骤如下:
(1). 将总体X的取值范围分成k个互不重叠的 小区间 I1, I2, …, Ik, I1 (a0,a1],I2 (a1,a2], ,Ik (ak 1,ak ],
a0 a1 a2 ak 1 ak .
H0:拉力强度 X ~ N(μ, σ2) .
解:本例中,并未给出各观测值 Xi 的具体值, 只给出了各观测值的取值范围,这样的数据
称为区间数据。样本均值与样本方差可通过
下列式计算:
X
1
n
k i1
ni
ai1 2
ai
,
S2
n
1
1
k
i1
ni
ai1 2
ai
2
nX
2
.
对正态总体N (μ,σ 2), 和 σ 2 的 极大似然估计为
(黄, 黄),(黄, 绿),(绿, 黄),(绿, 绿).
(黄, 黄),(黄, 绿),(绿, 黄),(绿, 绿).
孟德尔认为, 前三种配合使豆子呈黄色, 而第四种配合使豆子呈绿色。从古典概率的 观点看,黄色豆子出现的概率为3/4,绿色豆 子出现的概率为1/4。这就解释了黄绿颜色豆 子之比为什么总是接近 3:1 这个观察结果。
最后两组合并成一组(见表8.3)。
(3). 计算数据落入各子区间上的实际频数 fi 。
fi =﹟{ X1, X2, …, Xn ∈ Ii } , i=1, 2, …, 10 .
(4). 计算检验统计量的值
2 k [ fi npˆi ]2
i1 npˆi
22.15.
(5). H0的显著性水平为α 的检验 因为k=10,r=2,所以上述 χ 2分布的自







![[课件]第07章 拟合优度检验PPT](https://uimg.taocdn.com/67e50b4a25c52cc58bd6beb9.webp)

