【新课标】2018年最新沪教版(五四制)八年级数学下册同步练习：等腰三角形

轧东卡州北占业市传业学校等腰三角形一、课本稳固练习1．：在等腰ABC ∆中，︒=∠80B ,求：C ∠ 和 A ∠的度数。

2、等腰三角形的两边的长分别是5cm 和6cm ，那么这个等腰三角形的周长是_______cm ．3、如图，在△ABC 中，A=108°，AB=AC,BD 是角平分线。

求证：BC=AB+CD.4、：如图，在ABC ∆ 中，AC AB = ，BC BD =，EB DE AD ==。

求：A ∠的度数。

5、如图，在△ABC 中，AB=AC ，AD 是△ABC 的中线，AD=AE 。

〔1〕假设∠BAD=40o，那么∠EDC= ； 〔2〕假设∠BAD=70o，那么∠EDC= ； 〔3〕∠BAD 与∠EDC 在数量上有什么关系？并说明理由。

二、根底过关一、选择题〔A 〕等腰三角形的底角一定是锐角。

〔B 〕等腰三角形至少有两个角全等。

〔C 〕等腰三角形的顶角一定是锐角。

〔D 〕等腰三角形顶角的外角是底角的2倍。

2、如果三角形的三边c b a 、、满足()()()0=---a c c b b a ，那么这个三角形是〔 〕.〔A 〕等腰三角形 〔B 〕直角三角形〔C 〕等边三角形 〔D 〕锐角三角形3、等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是〔 〕.〔A 〕25° 〔B 〕40° 〔C 〕25°或40° 〔D 〕以上都不对4、等腰三角形的一个外角等于70°，那么底角的度数是〔 〕.〔A 〕110° 〔B 〕55° 〔C 〕35° 〔D 〕以上都不对5、三角形一边上的高和这边上的中线重合，那么这个三角形一定是〔 〕〔A 〕锐角三角形 〔B 〕 钝角三角形〔C 〕等腰三角形 〔D 〕等边三角形二、填空题1、：在等腰ABC ∆中，AC AB =，︒=∠80B ,求=∠C =∠A .2、等腰三角形的一个角等于︒42，那么它的底角为 .3、一等腰三角形两边为4,2，那么它的周长为 .4、一等腰三角形一腰上的中线把这个三角形的周长分成15cm 和18cm 两局部，那么这个等腰三角形的底边长是 .5、ABC ∆ 中，︒=∠65A ，︒=∠50B ，那么=AC AB : _________6、等腰三角形两个内角之比为1:2，求此等腰三角形的顶角和底角。

2017-2018学年（新课标）沪教版五四制八年级下册期中考试数学试卷说明：1、全卷共8页。

考试时间100分钟，满分150分．2、答卷前，考生必须将自己的座号、姓名、班级、学校按要求填写在密封线左边的空格内。

3、答题可用黑色钢笔、圆珠笔按各题要求答在试卷上，但不能用铅笔或红笔。

第Ⅰ部分 选择题（共30分）一、选择题。

（本题共10小题，每小题3分，共30分．每小题给出的 4 个选项中只有一个是正确的，请将所选选项的字母填在题目后面的括号内）1、在式子a 1，π　xy 2，2334a b c，x ＋　65， 7x ＋8y ，9 x +y 10　,xx 2　中，分式的个数是（ ）A.5B.4C.３D.２2、下列各式正确的是（ ） A ．c b a c b a +-=-- B.c ba cb a --=-- C ．c b a c b a +-=+- D.cba cb a ---=+- 3、如果把分式yx x+10中的x 和y 都扩大10倍,那么分式的值是( ) A.扩大100倍; B.扩大10倍; C.不变; D.缩小到原来的101 4、已知关于x 的函数y=k(x-1) 和ky x=-(0)k ≠,它们在同一坐标系中的图象大致是( )班 级考 号得分 评卷人姓 名密封线内不要答题5、已知函数xky =的图象经过点（2，3），下列说法正确的是（ ） A ．y 随x 的增大而增大 B.函数的图象只在第一象限 C ．当x ＜0时，必有y ＜0 D.点（-2，-3）不在此函数的图象上 6、若点(-2,y 1)、(-1,y 2)、(1,y 3)在反比例函数1y x=的图象上,则下列结论中正确的是( ) A.123y y y >>; B.213y y y >> C.312y y y >> D.321y y y >>7、如果矩形的面积为6cm 2，那么它的长ycm 与宽xcm 之间的函数关系用图象表示大致是（ ）A B C D8、现要装配30台机器,在装配好6台以后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成任爷,求原来每天装配机器的台数x,下列所列方程中不正确的是( ) A.62432x x +=; B.62432x x +=+; C.63032x x +=; D.303032x x+= 9、下列各组数中能够作为直角三角形的三边长的是（ ）A ．2，3，4B ．12，22，32C ．4，5，9D ．32，2，5210、若△ABC 中，AB=13，AC=15，AD 是BC 边上的高，且AD=12 ，则BC 的长为y xOyxOyxOy xO→← 3m4m “路”（ ）A ．14B ．4C ．14或4D ．以上都不对第Ⅱ部分 非选择题（共90分）二、填空题（本题共6小题，每小题3分，共18分．请把下列各题的正确答实填写在横线上）11、若分式11--x x 的值等于零，则x 的值等于 。

2017-2018学年（新课标）沪教版五四制八年级下册期中试卷八年级数学（满分100分，时间90分钟）题号一二三四五总分得分一、选择. 1. 下列函数中，是一次函数的是（）A．y=x2+2 B．C．y=kx+b（k、b是常数）D．y=x﹣12. 对于一次函数y=﹣3x+1，下列结论正确的是（）A．点（﹣1，3）在此函数图象上B． y的值随x值的增大而增大C．图象经过第一、二、三象限D．图象与x轴、y轴的交点分别为（，0），（0，1）3. 下列说法正确的是（）A．x2+3x=0是二项方程B．xy﹣2y=2是二元二次方程C．是分式方程D．是无理方程4. 下列方程中，有实数解的是（）A．=﹣1 B．=﹣x C．D．=0=05. 一次函数y=kx﹣k（k＜0）的图象大致是（）A ．B ．C ．D ．6. 如图，在四边形ABCD 中，若已知AB ∥CD ，再添加下列条件之一，能使四边形ABCD 成为平行四边形的条件是（ ）A ． ∠DAC=∠BCAB ． ∠DCB+∠ABC=180°C ． ∠ABD=∠BDCD ． ∠BAC=∠ACD二、填空7. 当x=时，一次函数y=2x ﹣1的值为0．8. 已知一次函数y=（1﹣m ）x+m ﹣2，当m 时，y 随x 的增大而增大． 9. 六边形ABCDEF 的内角和等于 ．10. 平行四边形ABCD 中，∠A ：∠B=2：1，则∠B 的度数为 ． 11. 解方程﹣=，设y=，那么原方程化为关于y 的整式方程是 ．12. 一次函数的图象过点（0，3）且与直线y=﹣x 平行，那么函数解析式是 ． 13. 方程的根是 ．14. 解关于x 的方程：b(x-1)=x+1 (b ≠1) ，可得x=________. 15. 已知关于x 的方程出现增根，则a 的值等于 .16. 如图，▱ABCD中，∠ABC=60°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，EF=，则AB的长是．17. 一次函数y1=kx+b与y2=x+a的图象如图，则不等式kx+b＞x+a的解集是．18.一次函数y=﹣x+3的图象分别与x轴、y轴交于点A、B，将线段AB绕点A顺时针旋转90°得到线段AC．则过B、C两点直线的解析式为___________三、简答19. 画出函数y=x﹣4的图像，求出该图像与坐标轴交点的坐标；并写出其向上平移3个单位后的图像的解析式.20. 解方程：．21. 解方程组：．22. 马小虎的家距离学校1800米，一天马小虎从家去上学，出发10分钟后，爸爸发现他的数学课本忘记拿了，立即带上课本去追他，在距离学校200米的地方追上了他，已知爸爸的速度是马小虎速度的2倍，求马小虎的速度．四、解答23. 如图，已知E、F分别为▱ABCD的对边AD、BC上的点，且DE=BF，EM⊥AC于M，FN⊥AC于N，EF交AC于点O，求证：EF与MN互相平分．24. 小明和爸爸进行登山锻炼，两人同时从山脚下出发，沿相同路线匀速上山，小明用8分钟登上山顶，此时爸爸距出发地280米．小明登上山顶立即按原路匀速下山，与爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地的路程y1（米）、y2（米）与小明出发的时间x（分）的函数关系如图．（1）图中a= ，b= ；（2）求小明的爸爸下山所用的时间．25. 如图，在平面直角坐标系中，函数y=﹣2x+12的图象分别交x轴、y轴于A、B两点，过点A的直线交y 正半轴于点M，且点M为线段OB的中点．（1）求直线AM的函数解析式．（2）试在直线AM上找一点P，使得S△ABP=S△AOM，求P坐标.（3）在坐标平面内是否存在点C，使以A、B、M、C为顶点的四边形是平行四边形？若存在，请直接写出点C的坐标；若不存在，请说明理由．八年级数学答案一、选择1. B2. D3. B4. C5. A6. A二、 填空7.8. m ＜1 9. 720° 10. 60° 11. 3y 2﹣4y ﹣3=0 12. y=﹣x+3 13. 214.11-+b b15. 16. 1 17. x ＜﹣2 18. 371+=x y 三、简答19.图准确2分，与x 轴交点（4,0） 与y 轴交点（0.-4）2分，平移后解析式：1-=x y 2分20. 解方程：．解答：解：方程化为， 1’ 两边平方得：， 1’∴，x 2﹣6x+9=15﹣x ，即x 2﹣5x ﹣6=0 2’ x=﹣1或x=6 1’ 经检验，x=﹣1是增根，所以原方程的根为x=6 1’21. 解方程组：．解答：解：由方程②得：（x+y）2=1，x+y=1，x+y=﹣1，2’即组成方程组或，2’解这个两个方程得：或，即原方程组的解为：或．2’22. 马小虎的家距离学校1800米，一天马小虎从家去上学，出发10分钟后，爸爸发现他的数学课本忘记拿了，立即带上课本去追他，在距离学校200米的地方追上了他，已知爸爸的速度是马小虎速度的2倍，求马小虎的速度．解答：解：设马小虎的速度为x米/分，则爸爸的速度是2x米/分，依题意得1’-- +10，3’解得x=80．2经检验，x=80是原方程的根．1’答：马小虎的速度是80米/分．1’23. 如图，已知E、F分别为▱ABCD的对边AD、BC上的点，且DE=BF，EM⊥AC于M，FN⊥AC于N，EF交AC于点O，求证：EF与MN互相平分．解答：证明：连接EN、FM，∵EM⊥AC，FN⊥AC，∴∠AME=∠EMN=∠FNC=∠FNM=90°，∴EM∥FN，1’∵四边形ABCD是平行四边形，1’∴AD∥BC，AD=BC，∴∠EAM=∠FCN，1’∵DE=BF，∴AE=CF，1’在△AEM和△CFN中∴△AEM≌△CFN（AAS），3’∴EM=FN，∵EM∥FN，∴四边形EMFN是平行四边形，2’∴EF与MN互相平分．124. 小明和爸爸进行登山锻炼，两人同时从山脚下出发，沿相同路线匀速上山，小明用8分钟登上山顶，此时爸爸距出发地280米．小明登上山顶立即按原路匀速下山，与爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地的路程y1（米）、y2（米）与小明出发的时间x（分）的函数关系如图．（1）图中a= 8 ，b= 280 ；2’+2’（2）求小明的爸爸下山所用的时间．解答：解：（1）由图象可以看出图中a=8，b=280，故答案为：8，280．（2）由图象可以得出爸爸上山的速度是：280÷8=35米/分，小明下山的速度是：400÷（24﹣8）=25米/分，2’∴小明从下山到与爸爸相遇用的时间是：（400﹣280）÷（35+25）=2分，∴2分爸爸行的路程：35×2=70米，2’∵小明与爸爸相遇后，和爸爸一起以原下山速度返回出发地．∴小明和爸爸下山所用的时间：（280+70）÷25=14分．2’. 如图，在平面直角坐标系中，函数y=﹣2x+12的图象分别交x轴、y轴于A、B两点，过点A 的直线交y 正半轴于点M，且点M为线段OB的中点．（1）求直线AM的函数解析式．（2）试在直线AM上找一点P，使得S△ABP=S△AOM，请直接写出点P的坐标．（3）在坐标平面内是否存在点C，使以A、B、M、C为顶点的四边形是平行四边形？若存在，请直接写出点C的坐标；若不存在，请说明理由．解答：解：（1）∵直线AB的函数解析式y=﹣2x+12，∴A（6，0），B（0，12）．2又∵M为线段OB的中点，∴M（0，6）．1’设直线AM的解析式为：y=kx+b，则，解得：，故直线AM的解析式y=﹣x+6；2’（2）设点P的坐标为：（x，﹣x+6），∴AP==|x﹣6|，过点B作BH⊥AM于点H，∵OA=OM，∠AOM=90°，∴∠AMO=45°，∴∠BMH=45°，∴BH= 6×=3，1’∵S△ABM=S△AOM，S△AOM=OA•OM=×6×6=18，S△ABP=AP•BH=×|x﹣6|×3，1’∴×|x﹣6|×3=18，解得：x=0或12，2’故点P的坐标为：（0，6）或（12，﹣6）．(3) （6，-6）、（6,6）、（-6,18）每个点1分。

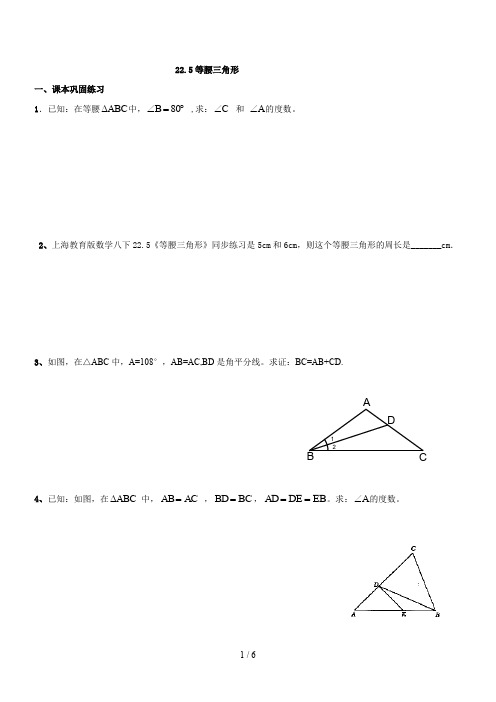
22.5等腰三角形一、课本巩固练习1．已知：在等腰ABC ∆中，︒=∠80B ,求：C ∠ 和 A ∠的度数。

2、上海教育版数学八下22.5《等腰三角形》同步练习是5cm 和6cm ，则这个等腰三角形的周长是_______cm ．3、如图，在△ABC 中，A=108°，AB=AC,BD 是角平分线。

求证：BC=AB+CD.4、已知：如图，在ABC ∆ 中，AC AB = ，BC BD =，EB DE AD ==。

求：A ∠的度数。

A CD 125、如图，在△ABC 中，AB=AC ，AD 是△ABC 的中线，AD=AE 。

（1）若∠BAD=40o，则∠EDC= ；（2）若∠BAD=70o ，则∠EDC= ；（3）∠BAD 与∠EDC 在数量上有什么关系？并说明理由。

二、基础过关一、选择题1、下列命题中的假命题是（ ）（A ）等腰三角形的底角一定是锐角。

（B ）等腰三角形至少有两个角全等。

（C ）等腰三角形的顶角一定是锐角。

（D ）等腰三角形顶角的外角是底角的2倍。

2、如果三角形的三边c b a 、、满足()()()0=---a c c b b a ，那么这个三角形是（ ）.（A ）等腰三角形 （B ）直角三角形（C ）等边三角形 （D ）锐角三角形3、等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是（ ）.（A ）25° （B ）40° （C ）25°或40° （D ）以上都不对4、已知等腰三角形的一个外角等于70°，那么底角的度数是（ ）.（A ）110° （B ）55° （C ）35° （D ）以上都不对5、三角形一边上的高和这边上的中线重合，则这个三角形一定是（ ）（A ）锐角三角形 （B ） 钝角三角形（C ）等腰三角形 （D ）等边三角形二、填空题1、已知：在等腰ABC ∆中，AC AB =，︒=∠80B ,求=∠C =∠A .2、已知等腰三角形的一个角等于︒42，则它的底角为 .3、已知一等腰三角形两边为4,2，则它的周长为 .4、一等腰三角形一腰上的中线把这个三角形的周长分成15cm 和18cm 两部分，则这个等腰三角形的底边长是 .5、ABC ∆ 中，︒=∠65A ，︒=∠50B ，则=AC AB : _________6、已知等腰三角形两个内角之比为1:2，求此等腰三角形的顶角和底角。

2017-2018学年（新课标）沪教版五四制八年级下册《13.3、13.4》同步测试题（范围：13.3一次函数与一次方程、一次不等式 13.4二元一次方程组的图象解法）一、慎重选择，展示技巧！（每小题4分，共32分） 1.函数y=12-x+3与x 轴的交点的横坐标为（ ）A ．-3B ．6C ．3D ．-6 2.一次函数1y kx b =+与2y x a =+的图象如图1所示，则下列结论①0k <；②0a >；③当3x <时，12y y <中，正确的有（ ） A ．0个B ．1个C ．2个D ．3个3.如图2，直线y kx b =+与x 轴交于点A （-4，0），则当y ＜0时，x 的取值范围是（ • ）A ．x ＞-4B ．x ＞0C ．x ＜-4D ．x ＜4.已知一次函数y kx b =+的图象如图3所示，则当0＜x ＜1时，y 的取值范围是（ • ）A ．y ＞0B ．y ＜0C ．-2＜y ＜0D ．y ＜-25.如果直线y=3x+6与y=2x-4的交点坐标为（a ，b ），则下列方程组中解是x ay b =⎧⎨=⎩的是（ • ）A ．3624y x y x -=⎧⎨+=-⎩ B ．3624y x y x -=⎧⎨-=-⎩ C ．3624x y x y -=-⎧⎨+=⎩ D ．3624x y x y -=-⎧⎨-=⎩6.直线AB ∥y 轴，且A 点坐标为（1，-2），则直线AB 上任意一点的横坐标都是 1，我们称直线AB 为直线x=1，那么直线y=2与直线x=-3的交点的坐标是（ ）A ．（-3，2）B ．（2，3）C ．（-2，-3）D ．（-3，-2）7.对于函数y=-x+4，当x ＞1时，y 的取值范围是（ ）A ．y ＜5B ．y ＞5C ．y ＜3D ．y ＞ 3xyO3 2y x a =+1y kx b =+图1 图28.已知方程2x+1=-x+4的解是x=1，则直线y=2x+1与y=-x+4的交点坐标为（ ） A ．（1，0） B ．（1，3） C ．（-1，-1） D ．（-1，5）二、精心填空，展示耐心！（每小题4分，共24分）9.关于x 的方程3x+4a=2的解是正数，则a ．10.用加减法解方程组53x y x y +=⎧⎨-=⎩得其解为，则直线y=-x+5和y=x-3的交点的坐标为．•11.已知关于x 的方程ax-5=6的解为x=3，则一次函数y=ax-11与x •轴的交点的坐标为．12.二元一次方程113y x =+和230x y -=的图象的交点的坐标为．13.已知3x-2y=0，且x-1＞y ，则x 的取值范围是．14.直线y=2x+1b 与y=x+2b 的交点坐标是（4，3），则当x_______时，直线y=2x+1b •上的点在直线y=x+2b 上相应的点的上方． 三、全面作答，展示智慧！（共34分） 15.（8分）已知一次函数y 1=-2x+1，y 2=x-2． ⑴当x 分别满足什么条件时，y 1=y 2，y 1＜y 2，y 1＞y 2？⑵在同一直角坐标系中作出这两个函数的图象，并用自己的话归纳出⑴中的答案与函数图象之间的关系．16.（8分）利用图象法解二元一次方程组：图3124x y y x +=⎧⎨-=⎩．17.（9分）在同一直角坐标系中画出一次函数y 1=-2x+1与y 2=2x-3的图象，并根据图象解答下列问题：⑴直线y 1=-x+1、y 2=2x-2与y 轴分别交于点A 、B ，请写出A 、B 两点的坐标；⑵写出直线y 1=-2x+1与y 2=2x-3的交点P 的坐标；⑶求△PAB 的面积．18.（9分）某学校为改善老师的办公条件，计划购买若干台电脑，现从两个电脑城了解到某品牌同一型号的电脑每台标价都是4000元，但学校集体购买都有一定的优惠．甲电脑城的优惠方法是：第一台按标价收费，其余每台可优惠15%.则甲电脑城的总收费y 1（元）与学校所买电脑的台数x 之间的关系式是．乙电脑城的优惠方法是：每台都优惠12%.则乙电脑城的总收费y 2（元）与学校所买电脑的台数x 之间的关系式是．⑴学校在什么情况下到甲电脑城购买更优惠？⑵学校在什么情况下到乙电脑城购买更优惠？四、自主探索，展示素质！（10分）19.某产品每件的成本是100元，为了解市场对该产品的认可规律，销售部门分别按两种方案组织了试销售，情况如下：方案A：固定以每件140元的价格销售，日销售量为50件；方案B：每天都适当调整售价，发现日销售量y （件）近似是售价x（元）的一次函数，且前三天的销售情况如下表所示：x（元）130 140 150 y（件）70 50 30 如果方案B中的第四天的售价为155元、第五天的售价为160元，那么前五天中，哪种方案的销售总利润大？备用题：1.张翔有将平时的零用钱节约一些存起来的习惯，他已经存了98元，从现在起每月固定存8元．⑴请写出张翔存款的总数y1（元）与从现在开始的月数x之间的函数关系式；⑵张翔的好朋友李飞以前没有存过零用钱，知道张翔存了98元零用钱后决定从现在起每个月存14元.请你在同一平面直角坐标系中分别画出张翔和李飞的存款总数与月份数的函数关系的图象．一年以后李飞的存款总数是多少？超过张翔了吗？•至少多少个月后李飞的存款总数才超过张翔？2.有两条直线y=kx+b和y=ax+3，学生甲求得它们的交点坐标为（2，-1），学生乙因抄错了a而求得它们的交点坐标为（1，4）.请求出这两条直线的解析式．《13.3、13.4》同步测试题参考答案： 1.B 2.B 3.C 4.C 5.D 6.A 7.C 8.B 9.＜1210.41x y =⎧⎨=⎩，41x y =⎧⎨=⎩11.（3，0） 12.（3，2）13.x ＜-214.x ＞415.⑴当y 1=y 2时，-2x+1=x-2，-3x=-3，所以x=1；当y 1＞y 2时，-2x+1＞x-2，-3x ＞-3，所以x＜1；当y 1＜y 2时，-2x+1＜=x-2，-3x ＜-3，所以x ＞1；即，当x=1时，y1=y2；当x＜1时，y1＞y2；当x＞1时，y1＜y2..⑵y1与y2的图象如图1所示．利用图象也能得出⑴中相同的答案，即两条直线的交点的横坐标就是y1=y2时x的值；直线y1=-2x+1位于直线y2=x-2上方的部分所对应的x 的取值范围就是第2问的答案；直线y1=-2x+1位于直线y2=x-2下方的部分所对应的x的取值范围就是第3问的答案.16.主要步骤是：⑴分别列表得到两个二元一次方程的两组解；⑵分别描点画出两个方程的图象；⑶找到两条直线的交点的坐标；⑷根据坐标写出方程组的解.答案为：12xy=-⎧⎨=⎩．17.①A（0，1）、B（0，-2）；②P（1，-1）；③1.5 .18.y1=4000+（1-15%）×4000（x-1），化简得y1=3400x+600；y2=（1-12%）×4000x，化简得y2=3520x；⑴当y1＜y2时，3400x+600＜3520x，即x＞5.所以当学校所买电脑的台数超过5时，去甲电脑城更优惠．⑵当y1＞y2时，3400x+600＞3520x，即x＜5.所以当学校所买电脑的台数小于5时，去乙电脑城更优惠．19.设y与x之间的函数关系式为y=kx+b，把x=130，y=70和x=140，y=50分别代入函数关系式中，得7013050140k bk b=+⎧⎨=+⎩，解得2330kb=-⎧⎨=⎩.所以，函数关系式为y=-2x+330．当x=155时，y=20；当x=160时，y=10.则方案A的总利润为（140-100）×50×5=10000（元）；方案B的总利润为30×70+40×50+50×30+55×20+60×10=7300（元）．所以，前5天中销售方案A获得的总利润大．备用题答案：1.⑴y1=98+8x；⑵设李飞的存款总数为y2，则y2=14x．图象略．当x=12时，y1=98+12×8=98+96=194；y2=14×12=168．所以一年后李飞的存款总数为168元，还没有超过张翔．当y2＞y1时，14x＞98+8x，x＞1613, 所以，至少17个月后李飞的存款总数才会超过张翔．2.根据题意得231214ak bk b+=-⎧⎪+=-⎨⎪+=⎩，解得295abk=-⎧⎪=⎨⎪=-⎩，所以两条直线得解析式分别为y=-5x+9，y=-2x+3.。

22.3 特殊的平行四边形一、课本巩固练习1、如图，矩形ABCD 内一点P ，PC=3，PD=4，PB=5，求PA 的长。

2、如图，在ABC ∆中， 90=∠BAC ，AD 是BC 边上的高，ABC ∠的平分线交AD 与点E ，EF//BC 交AC 于点F ，求证：AE=CF3、如图，在ABC ∆中，D 是AC 的中点，E 是线段BC 延长线上一点，过点A 作BE 的平行线与线段ED 的延长 线交于点F ，联结AE 、CE 。

（1）求证：AF=CE（2）若AC=EF ，试判断四边形AFCE 是什么四边形，并证明你的结论。

二、基础过关1、下列命题中是真命题的是（ ）A. 对角线互相垂直且相等的四边形是正方形B.有两边和一角对应相等的两个三角形全等C. 两条对角线相等的平行四边形是矩形D.两边相等的平行四边形是菱形2、关于下列结论，正确的是_______________________。

①有一组对边平行，且有两个角是直角的四边形是矩形；②两条对角线相等的四边形是矩形；③两组对边分别相等的四边形是矩形；④有一个角是60°的平行四边形是菱形；⑤有两边相等的平行四边形是菱形；⑥有一组邻边相等的矩形是正方形；⑦有三边相等，且有一个角是直角的四边形是正方形；⑧对角线相等且互相垂直平分的四边形是正方形；3、下列四边形中，不是矩形的是（ ）A. 三个角都是直角的四边形B.四个角都相等的四边形C. 一组对边平行且对角线相等的四边形D.对角线相等且互相平分的四边形4、在下列命题中，真命题是（ ）A. 两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C. 两条对角线互相平分的四边形是平行四边形D.两边对角线互相垂直且相等的四边形是正方形5、四边形ABCD 的对角线AC 、BD 相交于点O ，能判断它是正方形的条件是（ ）A. DA CD BC AB ===B.BD AC DO BO CO AO ⊥==,,C. ,,BD AC BD AC =⊥且AC 、BD 互相平分D.DA CD BC AB ==,6、□ABCD 的周长是60cm ，AC 、BD 相交于点O,AOB ∆的周长比BOC ∆的周长大8cm 。

P149 A组复习题1.已知：点A(a，b)与点B(c,d).（1）如果点A,B关于y轴对称，那么a,b,c,d应满足什么条件？（2）如果点A,B关于x轴对称，那么a,b,c,d应满足什么条件？答：（1）a=-c,b=d. （2）a=c,b=-d.2.直线l与直线y=2x关于y轴对称，写出直线l所表示的函数表达式.答：y=-2x3.已知：如图，在ΔABC中，∠BAC=90°，AC=2AB,点D是AC的中点.ΔEAD为等腰直角三角形，∠AED=90°.试猜想线段BE和EC的关系，并证明你的猜想.猜想：BE=EC, BE⊥EC.证明：∵AC=2AB,点D是AC的中点(已知)，AC (中点定义)∴AD=DC= 12∴AB=DC（等量代换）,又∵ΔEAD为等腰直角三角形（已知），∴AE=DE, ∠EAD=∠EDA=45°（等腰直角三角形定义），∴∠CDE=135°（平角定义）∵∠BAC=90°（已知），∴∠BAE=∠BAC+∠EAD=135°，∴∠BAE=∠CDE（等量代换）,在ΔABE和ΔDCE中AB=DC（已证）∠BAE=∠CDE（已证）AE=DE（已证）∴ΔABE≌ΔDCE（SAS）∴BE=EC(全等三角形对应边相等),∠AEB=∠DEC(全等三角形对应角相等),∵∠AEB+∠BED=∠DEC+∠BED(等式的性质)4.已知：ΔABC中，AB=AC,AD是BC边上中线，AB的垂直平分线交AD于点O,∠B的平分线交AD于点Ｉ.求证：（1）OA=OB=OC; （2）点Ｉ到BC,CA,AB的距离相等.证明：（1）∵OG是AB的垂直平分线（已知），∴OA=OB（线段垂直平分线上的点和这条线段两个端点的距离相等）又∵AB=AC,AD是BC边上的中线（已知），∴AD是BC边的垂直平分线（三线合一），∵点O在AD上（已知），∴OB=OC（线段垂直平分线上的点和这条线段两个端点的距离相等）,∴OA=OB=OC（等式的性质）.（2）∵AB=AC,AD是BC边上的中线（已知），∴AD是∠BAC的平分线，又是BC边上的高（三线合一），∵ＩB平分∠ABC,ＩE⊥AB,ＩF⊥AC（已知）,∴ＩE=ＩF=ＩD（角的平分线上的点到角的两边的距离相等）,即：点Ｉ到BC,CA,AB的距离相等.5.已知：如图，AD是ΔABC的角平分线，DE⊥AB,DF⊥AC,点E,F为垂足.求证：AD 垂直平分EF.证明：∵AD是∠BAC的角平分线，DE⊥AB,DF⊥AC（已知）,∴∠EAD=∠FAD（角平分线定义）,∠AED=∠AFD=90°（垂直的定义），在ΔAED和ΔAFD中，∠EAD=∠FAD（已证）,AD=AD（公共边）,∴ΔAED≌ΔAFD（AAS）, ∴AE=AF,DE=DF（全等三角形对应边相等）,∴点A,D都在EF的垂直平分线上（到线段两端距离相等的点在线段的垂直平分线上），∴AD垂直平分EF（两点确定一条直线）.6.已知：如图，ΔABC是等边三角形，BD是中线.点E在BC的延长线上，使CE=CD. 求证：DB=DE.证明：∵ΔABC是等边三角形（已知），∴∠ABC=∠ACB=60°（等边三角形定义），∵BD是中线（已知）.∴BD又是∠ABC的平分线（三线合一），∴∠DBC=30°（角平分线定义），∵CE=CD（已知）, ∴∠E=∠CDE（等边对等角）,又∵∠ACB=∠E+∠CDE=60°（三角形外角等于不相邻的两个内角和），即∠E=30°，∴∠DBC=∠E（等量代换）, ∴DB=DE（等角对等边）.7.求证：有两条高相等的三角形是等腰三角形.已知：如图，ΔABC中，BD,CE分别是AC,AB边上的高，且BD=CE.求证：ΔABC是等腰三角形.证明：∵BD,CE分别是AC,AB边上的高（已知），∴∠ADB=∠AEC=90°（垂直的定义），了在ΔABD和ΔACE中，∠A=∠A（公共角）,BD=CE （已知）,∴ΔABD ≌ΔACE （AAS ）,∴AB=AC （全等三角形对应边相等）,∴ΔABC 是等腰三角形（等腰三角形定义）.8.已知：如图，ΔABC 中，AD 是BC 边上的高，AB=AC,∠BAC=120°，垂足分别是E,F.求证：DE+DF=12BC. 证明：∵AB=AC （已知）,∴∠B=∠C （等边对等角）,∵∠BAC=120°（已知），∴∠B=∠C=30°（三角形内角和为180°），又∵DE ⊥AB,DF ⊥AC （已知）,∴DE=12BD,DF=12DC （在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半）,∴DE+DF=12BD+12DC=12BC （等量代换）. 9.已知：如图，在ΔABC 中，AB=AC,∠A=120°，AC 的垂直平分线EF 交AC 于点E,交BC 于点F. 求证：BF=2CF.证明：连接AF,∵AB=AC （已知）,∴∠B=∠C （等边对等角）,∵∠A=120°（已知），∴∠B=∠C=30°（三角形内角和为180°），∵EF 是AC 的垂直平分线（已知），∴AF=CF （线段垂直平分线上的点和这条线段两个端点的距离相等）,∴∠BAF=∠A-∠FAC=120°-30°=90°，∴BF=2AF（在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半）,∴BF=2CF（等量代换）.10.已知：如图，AD⊥DE,BE⊥DE,AC,BC分别平分∠DAB,∠ABE,点C在线段DE上.求证：AB=AD+BE.证明：过C作CF⊥AB,垂足为F,又∵CD⊥AD,CE⊥BE（已知）,AC平分∠DAB,BC平分∠ABE,∴CD=CF=CE（角的平分线上的点到角的两边的距离相等）,在RtΔACD和RtΔACF中，AC=AC（公共边）,CD=CF（已证）,∴RtΔACD≌RtΔACF（HL）,∴AF=AD（全等三角形对应边相等）,在RtΔBCE和RtΔBCF中，BC=BC（公共边）,CE=CF（已证）,∴RtΔBCE≌RtΔBCF（HL）,∴BF=BE（全等三角形对应边相等）,∴AB=AF+BF=AD+BE（等量代换）.11.已知：如图，在ΔABC中，∠A=90°，AB=AC,点D在BC上，BD=AB,作DE⊥BC,点E在边AC上.求证：（1）BE平分∠ABC;（2）AE=ED=DC.证明：(1)在RtΔABE和RtΔDBE中，BE=BE（公共边）,AB=DB（已知）,∴RtΔABE≌RtΔDBE（HL）,∴∠ABE=∠DBE（全等三角形对应角相等）,∴BE平分∠ABC（角平分线定义）;(2)∵∠A=90°，AB=AC（已知）,∴∠C=∠CBA=45°（等腰直角三角形定义），又∵DE⊥BC(已知),∴∠DEC=∠C=45°（三角形内角和180°），∴ED=DC（等角对等边）,∵RtΔABE≌RtΔDBE（已证）,∴AE=ED（全等三角形对应边相等）,∴AE=ED=DC（等式的性质）.12.已知：如图，在ΔABC中，以它的边AB,AC为边，分别在形外作等边三角形ABD,ACE,连接BE,DC. 求证：BE=DC.证明：∵ΔABD和ΔACE都是等边三角形（已知），∴AB=AD,AE=AC（等边三角形定义）,∠BAD=∠CAE=60°（等边三角形定义），∴∠BAD+∠BAC=∠CAE+∠BAC（等式的性质）即∠BAE=∠DAC,AB=AD（已证）,∠BAE=∠DAC（已证）,AE=AC（已证）,∴ΔABE≌ΔADC（SAS）,∴BE=DC(全等三角形对应边相等).13.已知：如图，线段CD与∠AOB,通过作图求一点P,使PC=PD,并且点P到∠AOB 两边的距离相等.14.已知：如图，RtΔABC中，∠C=90°，沿过点B的一条直线BE折叠这个三角形，使点C与边AB上的点D重合.要使D恰好为AB的中点，问还需增加一个什么条件？说明你增加的条件及依据.解：可以增加：∠A=30°或BC=½AB,或∠ABC=60°，或∠ABC=2∠A.理由：∵∠C=90°，∠A=30°，∴BC=½AB,由折叠可知BC=BD=½AB,∴D为AB的中点.B组复习题1.根据下列点的坐标的变化，判断它们进行了怎样的变换？（1）（-3，-1）（3，-1）；（2）（-5, 6）（-5，1）；（3）（4，3）（4，-3）；（4）（2，-3）（3，-2）.答;：(1)关于y轴对称（或沿x轴方向向右平移6个单位）.(2)沿y轴方向向下平移5个单位(或关于直线y=3.5x对称).(3)关于x轴对称（或沿y轴方向向下平移6个单位）.(4)关于直线y=-x对称（或先沿x轴方向向右平移1个单位，再沿y轴方向向上平移1个单位）.2. BD是ΔABC的角平分线，BD的垂直平分线交CA的延长线于点E.求证：∠EAB=∠EBC.证明：∵E在BD的垂直平分线上（已知），∴EB=ED（线段垂直平分线上的点到线段两端点的距离相等）,∴∠EBD=∠EDB（等边对等角）,∵BD平分∠ABC（已知）,∴∠ABD=∠DBC（角平分线的定义）,又∵∠EAB=∠EDB+∠ABD（三角形的一个外角等于它不相邻的两个内角和）,EBC=∠EBD+∠DBC,∴∠EAB=∠EBC（等量代换）3.已知：O是线段AB的中点，直线MN经过点O,点C,D在直线MN上，∠1=∠2=45°.（1）若点C与点O重合[图(1)],请直接写出AC与BD的数量关系和位置关系；（2）若点C,D不重合[图(2)],求证：AC=BD,AC⊥BD.（1）解：AC与BD的数量关系和位置关系：AC=BD, AC⊥BD.（2）证明：过B作BE//AC,交MN于点E,∴∠A=∠OBE（两直平行，内错角相等）,又∵O是线段AB的中点（已知），∴OA=OB（线段的中点定义）,在ΔOAC和ΔOBE中，∠A=∠OBE（已证）,∠AOC=∠BOE（对顶角相等）,OA=OB（已证）,∴ΔOAC≌ΔOBE（ASA）,∴AC=BE,∠OCA=∠OEB（全等三角形对应边、对应角相等）,∴∠1=∠BED（等角的补角相等）∵∠1=∠2=45°（已知），∴∠2=∠BED=45°（等量代换），∴BE=BD（等角对等边）,∠DBE=90°（三角形内角和等于180°），∴AC=BD（等量代换）,BE⊥BD（垂直的定义）∵BE//AC（已证）,∴AC⊥BD（垂直于两条平行线中的一条时必垂直于另一条）4.已知：如图，在ΔABC中，∠ACB=90°，D,E是边AB上的两点，且AD=AC,BE=BC. 求证：∠DCE=45°.证明：∵AD=AC,BE=BC（已知）,∴∠ACD=∠ADC,∠BEC=∠BCE（等边对等角）,又∵∠A+∠ACD+∠ADC=180°，∠B+∠BEC+∠BCE=180°（三角形内角和等于180°），即∠A+2∠ACD=180°①，∠B+2∠BCE=180°②，∴①+②得：∠A+∠B+2∠ACD+2∠BCE=360°，∴∠A+∠B+2∠ACD+2∠BCD+2∠DCE=360°，即∠A+∠B+2∠ACB+2∠DCE=360°，又∵∠ACB=90°,∠A+∠B+∠ACB=180°，∴2∠DCE=90°，∴∠DCE=45°.5.已知：如图，点D在等边三角形ABC的边AC上，点E在边AB的延长线上，使BE=CD,DE交BC于点P. 求证:PD=PE.证明：过D作DF//AB交BC于F,∴∠CDF=∠A,∠CFD=∠CBA（两直线平线，同位角相等）,∠FDP=∠E（两直线平行，内错角相等）,又∵ΔABC是等边三角形（已知），∴∠A=∠CBA=∠C=60°（等边三角形的三个角都相等，并且每个角都等于60°），∴∠C=∠CDF=∠CFD（等量代换）,∴ΔCDF是等边三角形（三个角都相等的三角形是等边三角形），∴CD=FD（等边三角形定义）,∵BE=CD（已知）,∴FD=BE（等量代换）,在ΔFDP和ΔBEP中，∠FDP=∠E（已证）,∵∠DPF=∠EPB（对顶角相等）,FD=BE（已证）,∴ΔFDP≌ΔBEP（AAS）,∴PD=PE（全等三角形对应边相等）.6.（1）已知：如图（1），在ΔABC中，∠ABC,∠ACB的平分线交于点O,过点O 的直线DE//BC,DE分别与AB,AC交于点D,E.求证：BD+CE=DE.（2）将（1）题条件“∠ACB的平分线”改为“∠ACB的外角平分线”，如图（2）所示.原来的关系式BD+CE=DE还成立吗？如果不成立，你能推断出BD,CE,DE存在的数量关系式吗？请证明你的推断.（1）证明：∵DE//BC（已知）,∴∠DOB=∠OBC,∠EOC=∠OCB（两直线平线，内错角相等）,又∵OB平分∠ABC,OC平分∠ACB（已知）,∴∠OBD=∠OBC,∠OCE=∠OCB（角平分线定义）,∴∠DOB=∠OBD,∠EOC=∠OCE（等量你换）,∴BD=DO,CE=OE（等角对等边）,∴BD+CE=DO+OE（等式的性质）,即BD+CE=DE.（2）解：不成立.BD,CE,DE存在的数量关系式：BD-CE=DE.证明：∵DE//BC（已知）,∴∠DOB=∠OBC,∠EOC=∠OCF（两直线平行，内错角相等）,∵OB平分∠ABC,OC平分∠ACF（已知）,∴∠OBD=∠OBC,∠OCE=∠OCF（角平分线定义）,∴∠DOB=∠OBD,∠EOC=∠OCE（等量代换）,∴BD=DO,CE=OE（等角对等边）,∴BD-CE=DO-OE（等式的性质）,即BD-CE=DE.C 组复习题1.已知：等腰三角形ABC 中，AB=AC.（1）P 为底边BC 上任一点，自点P 向两腰作垂线PE,PF,点E,F 为垂足.求证：PE+PF 等于定值；（2）若点P 在底边BC 延长线上时，情况如何？证明：（1）连接AP ,设腰上的高为h 1,由S ΔABC =S ΔPAB +S ΔPAC ,得12AB •PE+12AC •PF=12AB •h 1.又∵AB=AC,∴ PE+PF=h 1.故，PE+PF 等于定值.（2）证明：连接AP ,设腰上的高为h 1,由S ΔABC =S ΔPAB -S ΔPAC ,得12AB •PE -12AC •PF=12AB •h 1.又∵AB=AC,∴ PE -PF=h 1.故，PE -PF 等于定值.如果，点P 在底边CB 延长线上时，有PF -PE=h 1.2.已知：等边三角形ABC.（1）P 为ΔABC 内任一点，自点P 向三边作垂线PD,PE,PF,点D,E,F 为垂足.求证：PD+PE+PF 等于定值；（2）若点P 在ΔABC 外时，情况如何？(1)证明：连接PA,PB,PC, 设等边ΔABC 的高为h,由S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC ，得 12AB •PD+12BC •PE+12AC •PF=12BC •h.又∵AB=BC=AC,∴PD+PE+PF=h, 故：PD+PE+PF 等于定值.(2)当P 在BA 与CA 的延长线所围成的区域内时，证明：连接PA,PB,PC, 设等边ΔABC 的高为h,由S ΔABC =S ΔPBC -S ΔPAB -S ΔPAC ，得12BC•PE -12AB•PD -12AC•PF=12BC•h.又∵AB=BC=AC,∵PE -PD -PF=h,当P 在BA 与BC 的延长线所围成的区域内时，证明：连接PA,PB,PC, 设等边ΔABC 的高为h,由S ΔABC =S ΔPBC +S ΔPAB -S ΔPAC ，得12BC•PE+12AB•PD -12AC•PF=12BC•h.又∵AB=BC=AC,∵PE+PD -PF=h,当P在AC与BC的延长线所围成的区域内时，当P在AB与AC的延长线所围成的区域内时，当P在AB与CB的延长线所围成的区域内时，当P在CB与CA的延长线所围成的区域内时，可以用类似的方法计算.。

2017-2018学年（新课标）沪教版五四制八年级下册22.3 特殊的平行四边形一、课本巩固练习1、如图，矩形ABCD内一点P，PC=3，PD=4，PB=5，求PA的长。

2、如图，在ABC∆中， 90∠BAC，AD是BC边上的高，ABC=∠的平分线交AD与点E，EF//BC交AC于点F，求证：AE=CF3、如图，在ABC∆中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，联结AE、CE。

（1）求证：AF=CE（2）若AC=EF，试判断四边形AFCE是什么四边形，并证明你的结论。

二、基础过关1、下列命题中是真命题的是（）A. 对角线互相垂直且相等的四边形是正方形B.有两边和一角对应相等的两个三角形全等C. 两条对角线相等的平行四边形是矩形D.两边相等的平行四边形是菱形2、关于下列结论，正确的是_______________________。

①有一组对边平行，且有两个角是直角的四边形是矩形；②两条对角线相等的四边形是矩形；③两组对边分别相等的四边形是矩形；④有一个角是60°的平行四边形是菱形；⑤有两边相等的平行四边形是菱形；⑥有一组邻边相等的矩形是正方形；⑦有三边相等，且有一个角是直角的四边形是正方形；⑧对角线相等且互相垂直平分的四边形是正方形；3、下列四边形中，不是矩形的是（ ）A. 三个角都是直角的四边形B.四个角都相等的四边形C. 一组对边平行且对角线相等的四边形D.对角线相等且互相平分的四边形4、在下列命题中，真命题是（ ）A. 两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C. 两条对角线互相平分的四边形是平行四边形D.两边对角线互相垂直且相等的四边形是正方形5、四边形ABCD 的对角线AC 、BD 相交于点O ，能判断它是正方形的条件是（ ）A.DA CD BC AB === B.BD AC DO BO CO AO ⊥==,, C. ,,BD AC BD AC =⊥且AC 、BD 互相平分 D.DA CD BC AB ==, 6、□ABCD 的周长是60cm ，AC 、BD 相交于点O,AOB ∆的周长比BOC ∆的周长大8cm 。

一、 因动点产生的相似三角形问题例1如图1，将抛物线2y x =-平移，平移后的抛物线与x 轴交于点A （1-，0）和B （3，0），与y 轴交于点C ，顶点为D 。

（1）求平移后的抛物线的表达式和点D 的坐标； （2）∠ACB 和∠ABD 是否相等？请证明你的结论；（3）点P 在平移后的抛物线的对称轴上，且△CDP 与△ABC 相似，求点P 的坐标。

图1第十五讲 压轴题复习如图1，在平面直角坐标系xOy 中，顶点为M 的抛物线2(0y ax bx a =+>）经过点A 和x 轴正半轴上的点B ，AO OB == 2，0120AOB ∠=．（1）求这条抛物线的表达式； （2）联结OM ，求AOM ∠的大小；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．图1在平面直角坐标系中，一个二次函数的图象经过(1,0)(3,0)、两点。

A B（1）写出这个二次函数图象的对称轴；（2）设这个二次函数图象的顶点为D，与y轴交于点C，它的对称轴与x轴交于点E，连接AC、DE和DB，当AOC∆相似时，求这个二次函数的表达式。

∆与DEB例4如图1，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过A、O、B的抛物线的解析式；（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．图1例5如图1，已知点A （2，0），点B 在y 轴正半轴上，且OA OB 21=．将点B 绕点A 顺时针方向旋转 90至点C ．旋转前后的点B 和点C 都在抛物线c bx x y ++-=265上．（1）求点B 、C 的坐标； （2）求该抛物线的表达式；（3）联结AC ，该抛物线上是否存在异于点B 的点D ，使点D 与AC 构成以AC 为直角边的等腰直角三角形？如果存在，求出所有符合条件的D 点坐标，如果不存在，请说明理由．图1例6如图1，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经过 点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，23-），点M 是抛物线C 2：m mx mx y 322--=（m ＜0）的顶点． （1）求A 、B 两点的坐标； （2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．图1四、因动点产生的平行四边形问题例7如图1，抛物线254y x bx c =-++与y 轴交于点A (0,1)，过点A 的直线与抛物线交于另一点B 5(3,)2，过点B 作BC x ⊥轴，垂足为C ．（1）求抛物线的表达式；（2）点P 是x 轴正半轴上的一动点，过点P 作PN x ⊥轴，交直线AB 于点M ，交抛物线于点N ，设OP 的长度为m ．①当点P 在线段OC 上（不与点O 、C 重合）时，试用含m 的代数式表示线段PM 的长度；②联结,CM BN ，当m 为何值时，四边形BCMN 为平行四边形？如图1，点A （2，6）和点B （点B 在点A 的右侧）在反比例函数的图像上，点C 在y 轴上，BC //x 轴，2tan =∠ACB ，二次函数的图像经过A 、B 、C 三点． （1）求反比例函数和二次函数的解析式；（2）如果点D 在x 轴的正半轴上，点E 在反比例函数的图像上，四边形ACDE 是平行四边形，求边CD 的长．图1如图1，已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点．（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．图1五、因动点产生的梯形问题例10如图1，已知二次函数mx x y 22+-=的图像经过点B （1,2），与x 轴的另一个交点为A ，点B 关于抛物线对称轴的对称点为C ，过点B 作直线BM ⊥x 轴垂足为点M ． （1）求二次函数的解析式； （2）在直线BM 上有点P （1，23），联结CP 和CA ，判断直线CP 与直线CA 的位置关系， 并说明理由；（3）在（2）的条件下，在坐标轴上是否存在点E ，使得以A 、C 、P 、E 为顶点的四边形为直角梯形，若存在，求出所有满足条件的点E 的坐标；若不存在，请说明理由。

三角形与四边形的综合题1．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）．（A）①②③（B）①④⑤（C）①②⑤（D）②⑤⑥2．把“直角三角形、等腰三角形、•等腰直角三角形”填入下列相应的空格上：（1）正方形可以由两个能够完全重合的_________拼合而成；（2）菱形可以由两个能够完全重合的_________拼合而成；（3）矩形可以由两个能够完全重合的________拼合而成．3．一张矩形纸片按如图甲或乙所示对折，然后沿着图丙中的虚线剪下，得到①，•②两部分，将①展开后得到的平面图形是（）．（A）三角形（B）矩形（C）菱形（D）梯形4．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．•再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（• ）．1.用一把刻度尺来判定一个零件是矩形的方法是. 2．如果边长分别为4cm和5cm的矩形与一个正方形的面积相等，那么这个正方形的边长为______cm．3．如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为cm2．4．如图1，DE ∥BC ，DF ∥AC ，EF ∥AB ，图中共有_______个平行四边形．5若四边形ABCD 是平行四边形，请补充条件 (写一个即可)，使四边形ABCD 是菱形．6．，在平行四边形ABCD 中，已知对角线AC 和BD 相交于点O ，△ABO 的周长为17，AB ＝6，那么对角线AC ＋BD ＝ ⒎以正方形ABCD 的边BC 为边做等边△BCE ，则∠AED 的度数为 .8．延长正方形ABCD 的边AB 到E ，使BE ＝AC ，则∠E＝ °9．已知菱形ABCD 的边长为6，∠A ＝60°，如果点P 是菱形内一点，且PB ＝PD ＝2那么AP 的长为 ．10．在平面直角坐标系中，点A 、B 、C 的坐标分别是A(－2，5)，B(－3，－1)，C(1，－1)，在第一象限内找一点D ，使四边形ABCD 是平行四边形，那么点D 的坐标是 ．1如图1，在四边形中，，分别是的中点，连结并延长，分别与的延长线交于点，则（不需证明）．（温馨提示：在图1中，连结，取的中点，连结，根据三角形中位线定理，证明，从而，再利用平行线性质，可证得．）问题一：如图2，在四边形中，与相交于点，，分别是的中点，连结，分别交于点，判断的形状，请直接写出结论．问题二：如图3，在中，，点在上，，ABCD AB CD =E F 、BC AD 、EF BA CD 、M N 、BME CNE ∠=∠BD BD H HE HF 、HE HF =12∠=∠BME CNE ∠=∠ADBC AB CD O AB CD =E F 、BC AD 、EF DC AB 、M N 、OMN △ABC △AC AB >D AC AB CD =E F、分别是的中点，连结并延长，与的延长线交于点，若，连结，判断的形状并证明．2已知中，为边的中点， 绕点旋转，它的两边分别交、（或它们的延长线）于、 当绕点旋转到于时（如图1），易证 当绕点旋转到不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，、、又有怎样的数量关系？请写出你的猜想，不需证明．3已知：的高AD 所在直线与高BE 所在直线相交于点F ．（1）如图l ，若为锐角三角形，且，过点F 作，交直线AB 于点G ，求证：； （2）如图 2，若，过点F 作，交直线AB 于点G ，则FG 、DC 、AD 之间又有怎样的数量关系？请写出你的猜想，不需证明．4已知：正方形ABCD 中，45MAN ∠=o ，MAN ∠绕点A 顺时针旋转，它的两边分别交CB DC ，（或它们的延长线）于点M N ，． BC AD 、EF BA G 60EFC ∠=°GD AGD △Rt ABC △90AC BC C D ==︒，∠，AB 90EDF ∠=°，EDF ∠D AC CB E F ．EDF ∠D DE AC ⊥E 12DEF CEF ABC S S S +=△△△．EDF ∠D DE AC 和DEF S △CEF S △ABC S △ABC △ABC △45ABC ∠=°FG BC ∥FG DC AD +=135ABC ∠=°FG BC ∥A C D F E N M O B C D H A F NM1 2 图1 图2 图3 AB C D F G E A E C F B D 图1 图3 AD FE C B A D BC E 图2F A E C B DFG （图2） AEC D G B F当MAN ∠绕点A 旋转到BM DN =时（如图1），易证BM DN MN +=．（1）当MAN ∠绕点A 旋转到BM DN ≠时（如图2），线段BM DN ，和MN 之间有怎样的数量关系？写出猜想，并加以证明．（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间又有怎样的数量关系？请直接写出你的猜想．5已知：如图，BD 、CE分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别为F 、G ，连结FG ，延长AF 、AG 与直线BC 相交，易证：，若： （1）BD 、CE 分别是△ABC 的内角平分线（如图2）；（2）BD 为△ABC 的内角平分线，CE 为△ABC 的外角平分线（如图3），则在图2、图3两种情况下，线段FG 与△ABC 三边又有怎样的数量关系？请写出你的猜测，并对其中的一种情况进行证明。