当前位置：文档之家 › 画法几何题库之换面法

画法几何题库之换面法

  • 格式：doc
  • 大小：5.57 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

画法几何换面法、综合问题大理

画法几何换面法、综合问题大理

回
称之为满足该条件的轨迹），多个条件则形成多个轨迹，这些轨迹的 退
交集即为所求，再弄清该集合是什么形状，在投影图上如何实现。
出
解题中的常见轨迹 综合性问题解法举例（一） 距离和角度的度量
综合性问题解法举例（二）
本章结束
页上一 返 回
退出
• THANK YOU!
回
(4)把一般位置平面变为投影面平行面
退
出
§6-5 综合性问题解法举例
工程实际抽象出来的几何问题，如距离、角度的度量；点、线、
面的定位等，并不是单纯的平行、相交、垂直问题，而多是较复杂的
综合问题，其突出特点是要受若干条件的限制，求解时往往要同时满 上
足Hale Waihona Puke 个条件。一节解决此类问题的方法通常是：分析、确定解题方案及投影图上实
画法几何换面法、综合问题大理
§6-2 换面法
一、换面法的基本概念 二、点的投影变换规律
1、点的一次变换
点在V1/H 体系中的投影 点在V/H1体系中的投影
上一
2、点的两次变换
节
3、四个基本问题
下一
(1)把一般位置直线变为投影面平行线
节
(2)把一般位置直线变为投影面垂直线
返
(3)把一般位置平面变为投影面垂直面
现。分析时，首先根据给出已知条件和求解要求，想出已知空间几何 模型，然后进行空间思维，想象出最终结果的空间几何模型，最后确
下 一页
定从已知几何模型到最终结果几何模型的空间解题步骤。 返
如果最终结果的几何模型难以直接确定，则常采用“轨迹法”， 即逐个满足限制条件，找出满足每一个条件的无数解答的集合（通常

4换面法

4换面法

a'
x
O x1
四、换面法的应用——举例
[例题2] 已知C与直线AB的投影，求点C到AB直线间的距离。
a1
a' k1 b1 k' c' H X V b' a k c b'2 a'2 k'2 c'2 c1
距离
b
空间分析
四、换面法的应用——举例
[例题3] 求交叉两直线AB和CD间的最短距离EF ，如图所示。
2．投影面保持不动，使空间几何要素绕某一轴线旋转到 平行或垂直于投影面的特殊位置，然后找出其旋转后的新投 影。这种方法称为——旋转法。
这里仅讲换面法
二、点的换面规律
V c' C b1' A X1 bB c a' b' X
c1 ' V1 a1'
a H
V/H 体系变为V1/H 体系
新投影面必须满足下列两条原则：
b a
H
a
作图特点：
① 新的投影轴必须平行于直线的一个投影，且可求出直线的实长和倾角 ②求直线对某投影面的倾角，新投影轴必须平行于该投影面直线的投影
三、换面法的基本作图
将一般位置直线变换成投影面平行线，并求出角？ a'
b' V X H a b
a1

b1
三、换面法的基本作图
2、将平行线变换成垂直线 V a H1 a1 b1 V X H b
3、将一般位置平面变换成垂直面
V
a
b d c A b a d C c B D b1 d1 c1 H1 a b
a1
X
c b d
V X H a
H
c

第7讲换面法

第7讲换面法
根据要求得到的结果确定出有关几何元素对新投影面应处于什么样的特殊位置垂直或平行据此选择正确的解题思路与方在具体作图过程中要注意新投影与原投影在变换前后的关系既要在新投影体系中正确无误地求得结果又能将结果返回到原投影体系中去
第七讲
一、问题的提出
投影变换
★ 如何求一般位置直线的实长？ ★ 如何求一般位置平面的真实大小？ 解决方法：更换投影面。 换 面 法： 物体本身在空间的位置不动，而用某 一新投影面（辅助投影面）代替原有投影 面，使物体相对新的投影面处于解题所需 要的有利位置，然后将物体向新投影面进 行投射。
换面法的四个基本问题：
1. 把一般位置直线变成投影面平行线 变换一次投影面 2. 把一般位置直线变成投影面垂直线 变换两次投影面 3. 把一般位置平面变成投影面垂直面 变换一次投影面 需先在面内作一条投影面平行线
4. 把一般位置平面变成投影面平行面 变换两次投影面
四、解题时一般要注意下面几个问题： ⒈ 分析已给条件的空间情况，弄清原始条件中 物体与原投影面的相对位置，并把这些条件 抽象成几何元素（点、线、面等）。 ⒉ 根据要求得到的结果，确定出有关几何元 素对新投影面应处于什么样的特殊位置（垂 直或平行），据此选择正确的解题思路与方 法。 ⒊ 在具体作图过程中，要注意新投影与原投影 在变换前后的关系， 既要在新投影体系中正 确无误地求得结果，又能将结果返回到原投 影体系中去。

V X
ax
.
a1'
H
ax1
P1 H X1
ax
X


ax1 a
H X1
a

a1ax1 = aax 一般规律： 点的新投影和与它有关的原投影的连线，必垂直 于新投影轴。 点的新投影到新投影轴的距离等于被代替的投影 到原投影轴的距离。

换面法

换面法
应用换面法在V1/H2体系中解题：
解题步骤： 1.将两已知平行 直线构成的平面 经两次变换，变 变换，变成投影 面平行面 2.求作EF 的实长
实长
例: 平行四边形ABCD 给定一平面，试求点S 至该平面的距离 空间分析：
. 距离
解题步骤：
1.将平面ABCD 变换为新投 影面的垂直面 2.点S 随之变换 3.过S 作ABCD 的垂线,s1’k1’ 即为所求
解题步骤：
1.将直线EF 变换 为新投影面的 平行线 2.点A 随之变换 3.过a1’作e1’f1’的 垂线,得k1’ 4.将k1’a1’返回原 体系
例：试求某炼油厂的球罐A到输油管BC的最短净距离（5-9）
a2
b’
b’ c’
L
c2 (b2)
a’
X
b a
V O H
a’ c’ a1’ b a
b1 ’
保留投影面
保留投影
.
v1
新投影
作图步骤： 1)画X1 轴； 2)过a’ 作X1 轴的垂线； 3)在垂线上截取 新投影面
a1aX1 = aaX 。
2）点在V/H1体系中的投影 （用Ｈ1面代替Ｈ面，求点的新投影）
H1ห้องสมุดไป่ตู้
保留投影 新投影
旧投影
新投影面的设立原则：
１．新投影面必须设立在使空间元素处在有利于解题的位置 ． ２．新投影面必须垂直于原有投影面体系中的一个投影面．
∥
∥
∧
二、例题
例：求图中所示下料漏斗两相邻斗壁的夹角θ（例5-8）
(a’) f’ (d’)
(b’) (c’) e’
a b e f d
d1 a1 f1 c1 e1 b1 d’2 (c’2 ) θ a’2

画法几何及工程制图习题答案

画法几何及工程制图习题答案
c1’
e1’
5
b1’
11-2 直线DE与三角形ABC平行，距离为15。求作DE的投影。
b’ e’
a’
c’
b
m’
e‘ d‘
a
e
15
e
m
d
c
11-3 过点S作平面既垂直于平面CDE，又垂直于直线AB。并求ab.
s1
b1
b’ c’
a1
11 1’
a’
s’
b 1s
a
c
a‘1
b’1
s’1
c1’d1’
H e1’ V1 X1
e’
a1b1
m’
g’ b’
11
n’
c1
a’
d’ f’ f
1’
c’
1 a
b
n
m g
c
a1’ 11’
d2e2 11’
11-10 作直线MN与DE、FG相交，与三角形ABC垂直。
e’
1’ g’ b’
k’
a’
2’ f’
d’
c’
f
a
b
1
d
k
2
g
c
11-11 正方形ABCD与H面的夹角α=30，AD边在AE上，B点到MN等距。
c’
a’ d’
d a
c
a2
d2 60
b’
c2
b2
a1’ b1’
d1
b
c1’
11-6求两平面的夹角。
a’
d’ c’
b’ c
a c1
c2
a1b1
a1
θ
d2
d
b b1 d1
11-7过A作直线与AB、CD均相交

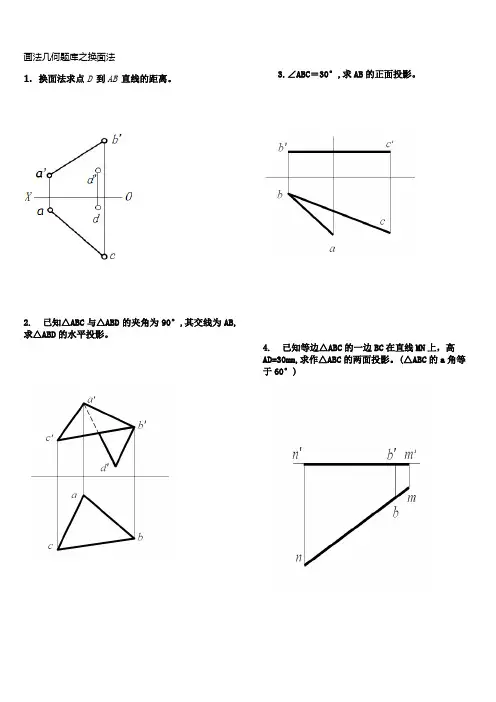
画法几何题库之换面法

画法几何题库之换面法

画法几何题库之换面法1.换面法求点D 到AB 直线的距离。

2.已知△ABC与△ABD的夹角为90°,其交线为AB,求△ABD的水平投影。

3.∠ABC＝30°,求AB的正面投影。

4.已知等边△ABC的一边BC在直线MN上，高AD=30mm,求作△ABC的两面投影。

(△ABC的a角等于60°)5 过点A作一正方形ABCD,其边BC在直线MN上，求作正方形的两面投影。

6求交叉二直线AB和CD的公垂线及实长。

7.求△ABC绕AB轴转90°后的新投影,并分析有几解？8直线AB 上一点C距点A为30mm，过点C作直线AB的垂线，且与直线EF相交，求作该直线的两面投影。

9.已知等边三角形ABC的C点在V面内，求作此三角形的两面投影，问有几个答案？若ab按箭头方向平移，移至何处时，只有一个答案，再移动时，情况如何？10在ABC内作直线DE，使它平行于BC边，且相距15mm。

11已知平面四边形ABCD的点A在V面内，距H面为25mm，试完成平面四边形的投影，若点A到H面的距离不限，则点A应在什么地方？12求与二直线AB，AC等距的点的轨迹。

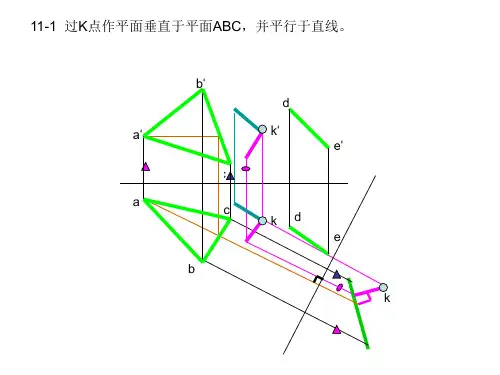
13求直线AB与平面的交点K,并判断可见性。

(1)(2)14已知BD为菱形的一对角线，顶点A在直线EF上，求菱形ABCD的投影。

15作一次换面，使交叉两直线AB及CD的投影面上的投影相互平行。

16求直线AB与△CDE的夹角17在直线AB上找一点K，使它与△ MNC及△MND等距。

18求直线AB与月BC的夹角19 202122.2324 2526（注：文档可能无法思考全面，请浏览后下载，供参考。

可复制、编制，期待你的好评与关注！）。

画法几何试题

画法几何试题

二、点、直线和平面
2-1 根据点的空间位置，画出点的投影图。
班级
姓名
学号
u 1
2-2 根据点的投影图，画出点的空间位置。
班级
姓名
学号
2-3 根据点到投影面的距离，画出点的三面投影。
点 到H面为 到V面为 到W面为
2
2-4 根据点的坐标，画出点的投影图和空间位置。 (1) A(30、20、15），B（20、25、0），C（10、0、0）
d
4-12 用换面法作一等边三角形ABC，使其与V面的倾角为30度。
c' a' X2
X
10
a
10
b' c1
b a1( b 1 )
c
28
4-13 用换面法求两面夹角的实际大小。
b'
a' X
a
c' d'
c
b d
4-14 已知点A到平面BCD的距离为15，用换面法求a。
b' X
b
d' a' c'
d ac
5-15 补全三棱锥截切后的水平投影和侧面投影。
5-16 补全三棱锥穿孔后的水平投影和侧面投影。
36
5-17 求作直线AB与三棱柱的贯穿点，并求其侧面投影。
5-18 求作直线AB与三棱锥的贯穿点，并求其侧面投影。
5-19 求作直线AB、CD与三棱柱的表面交点。
5-20 求直线AB与该平面体的表面交点，并求其侧面投影。
b 26
X
4-9 用换面法求平面四边形ABCD的实形。 a'
d'
b' X
c'
c
d

画法几何 投影变换法换面

画法几何 投影变换法换面

四、解题时一般要注意下面几个问题：
⒈ 分析已给条件的空间情况，弄清原始条件中物体 与原投影面的相对位置，并把这些条件抽象成几 何元素（点、线、面等）。
⒉ 根据要求得到的结果，确定出有关几何元素对新 投影面应处于什么样的特殊位置（垂直或平行）， 据此选择正确的解题思路与方法。
⒊ 在具体作图过程中，要注意新投影与原投影在变 换前后的关系， 既要在新投影体系中正确无误地 求得结果，又能将结果返回到原投影体系中去。
垂直面。
思考：
X
若变换H面，需在面
内取什么位置直线？
正平线！
d b
A
a
c
D B
d b H
P1 C c1
a1 d1
c
b1
X1
例：把三角形ABC变换成投影面垂直面。
b
a
d
作 图 过 程：
★ 在平面内取一条水平
c
XV H
线AD。
a
b
★ 将AD变换成新投影
d.
面的垂直线。
c
H
●α
●
●
反映平面对哪
X1 P1 c1 a1 d1 b1 个投影面的夹角？
15 b2
a2 e2
e1
d2
c2
e d
ed
小结
本章主要介绍了投影变换的一种常用方法 ——换面法。
一、 换面法就是改变投影面的位置，使它与所给物 体或其几何元素处于解题所需的特殊位置。
二、 换面法的关键是要注意新投影面的选择条件， 即必须使新投影面与某一原投面保持垂直关系， 同时又有利于解题需要，这样才能使正投影规 律继续有效。
换面法—空间几何元素的位置保持不动，用新的投影面 来代替旧的投影面，使对新投影面的相对位置变成有利 解题的位置，然后找出其在新投影面上的投影。

画法几何及工程制图复习题

画法几何及工程制图复习题
画法几何及工程制图复习题
一、填空题
1、在画法几何中,一些常用的符号代表不同的含义：H代表（）、V代表（）、W代表（）。OX代表投影轴，（）的交线。
2、根据投射线的类型,投影法可分为（）和（）两种。
3、在某一投影面内的点，到该投影面内距离为( )，所以它在该投影面上的投影与其本身( )，另外两个投影位于相应的( )上。
（3）点的侧面投影到OY 的距离，等于点的正面投影到OX轴的距离，都反映点到H面的距离。
（4）点的水平投影到OY 距离，等于点的正面投影到OZ轴的距离，都反映点到W面的距离。
2、什么叫透视投影?
透视投影属于中心投影,就是把物体投影到投影面上时,所有的投影线都是从一个称为投影中心的点出发,所得到的透视投影与观察物体所得到的印象基本一致,富有立体感和真实感。在建筑设计过程中，常用这种投影来表现建筑物建成后的外貌，用以研究建筑物的空间造型和立面处理。
6、钢桁架节点图的画法是怎样的？
（1）、先用细线画出各杆件的轴线位置。
（2）、按照尺寸画出节点板、下弦杆、竖杆和斜杆；平面图上还需画出下平纵联的节点板及两根斜杆。
（3）、按照尺寸画出螺栓孔与泄水孔。
（4）、画填板和拼接板以及杆件的断面和不可见的轮廓线。
（5）、标注尺寸。
（6）、检查无误后进行描深。
（7）、填写尺寸数字、技术说明和标题栏。
答案：
6、如图所示，已知组合体的正面投影和侧面投影，补画其水平投影。
答案：
7、判断下图中各直线的位置关系
8、如图所示，过点A作平面与直线MN垂直。
答案：
9、如图所示，已知组合体的水平和侧面投影，补画其正面投影
答案：
10、判断下列各平面是什么位置平面。
11、上图为下图的中心剖面视图，补全上图中的剖面线。

画法几何制图—换面法[1]

画法几何制图—换面法[1]

三峡大学
19
1.用换面法在直线AB上取一点C，使AC=25。 1.用换面法在直线AB上取一点C AC=25。 用换面法在直线AB上取一点
c′
c
a ′1
c′1 b ′1
三峡大学
20
2.求 ABC与EF的交点 并判别可见性. 的交点， 2.求△ABC与EF的交点，并判别可见性.
e′ ′ a′ ′
k1 V H d′
换面法
一、问题的提出(实物) 实物)
如何求一般位置直线的实长？ 如何求一般位置直线的实长？变成投影面平行线 解决方法：更换投影面V为 解决方法：更换投影面 为V1//AB。 。
反映实长 V1
b′ ′ a′ ′
V H
a′ ′
V
A B a
a1 b1
b′ ′
X
b a
H
H
b
三峡大学
1
换 面 法：
物体本身在空间的位置不动， 物体本身在空间的位置不动，而用某一 新投影面（辅助投影面）代替原有投影面， 新投影面（辅助投影面）代替原有投影面， 使物体相对新的投影面处于解题所需要的特 殊位置，然后将物体向新投影面进行投射。 殊位置，然后将物体向新投影面进行投射。
AD C B a≡b≡d ≡ ≡ H2 X
c′ ′
V H
作图: 作图 d′ ′
b′ ′
a′ ′
c a
.
b
距离
d
a'1 d'1
.
H X1 V 1
b'1. a2b2 d2
c2
如何确定d 如何确定 1点 的位置？ 的位置？
c
c'1
V1 H2 X2
过c1作线平行于x2轴。

画法几何试题

画法几何试题

一、填空题（共 10 分，每空 1 分）1、正投影法的投影规律为、和。

2、正等轴测图各轴向伸缩系数均相等，为了作图方便普通采用简化的轴向伸缩系数，既p=q=r= 。

轴间角∠XOY=∠YOZ=∠ZOX== ，其中，OZ 轴规定画成方向。

3、平面与圆柱体相交，当截平面平行于圆柱轴线时截交线为，当截平面垂直于圆柱轴线时截交线为，当截平面倾斜于圆柱轴线时截交线为。

4、建筑物上与画面相交的平行直线在透视图中交于一点，称为。

二、单选题（共 10 分，每小题 1 分）1、当两个点的y 和z 坐标相似时，它们在（）投影面上的投影重叠为一点。

A V 面B H 面C W 面D V 和H 面2、当直线（）投影面时，投影会反映实长；A 平行于B 垂直于C 倾斜于D 重叠3、铅垂线的（）投影积聚成一点。

A V 面B H 面C W 面D V 和H 面4、在建筑图上加画阴影，普通采用的光线方向是：从左、前、上方射向右、后、下方，使光线的三个投影对投影轴都成（）角。

A 30°B 45°C 90°D 120°5、如图所示，图中所标注的角应为（）角。

A αB βC γD θ6、如图能够判断，AB 为（）。

A 水平线B 正平线C 侧平线D 普通位置直线7、平面图形为水平面时，它的（）面投影反映平面图形的实形。

A V 面B H 面C W 面D 以上都不对8、透视投影是（）投影。

A 平行B 中心C 斜D 正9、规定出物体的阴影，重要是求出物体上（）的影。

A 各顶点的B 全部棱线C 阴线D 全部面10、下面有关轴测投影的说法哪一种是对的的？( )A 直观性强，有一定的度量性B 含有真实感，但作图复杂费时C 绘图简便，有立体感，无度量性D 绘图简便，度量性好，无立体感a’ b’ba 三、判断题（共 10 分，对的打“√”，错的打“×”，每小题 1 分）1、与 v 面垂直的直线称为铅垂线。

2、以始终母线平行于一条轴线旋转一周既得圆锥面。

5章-换面法

5章-换面法

对平面：若求角，则将平面上的水平线换成垂直线 （即换V面，新轴垂直于水平线的H投影）； 若求β角，则将平面上的正平线换成垂直线 （即换H面，新轴垂直于正平线的V投影）。
[例1] 求点A到直线BC的距离和垂足的投影。 §6-3 十换二面五法规的划应教用材 例 1 ： 求 点 到 一 般 线 距 离
a'
O
X
a
绕铅垂轴旋转
b 轴线通过A点 d1
d' 绕正垂轴旋转
轴线通过C点
c' O
c
d
例
旋转法 (绕投影面垂直线旋转）
[例] 求铅垂面ABC的实形。
b1'
b'
十二五规划教材
垂 直 面 转 为 平 行 面
c1'
实形
c'
X
c1
b1
a' a
b
O
绕铅垂轴旋转 轴线通过A点
c
旋转法 (绕投影面垂直线旋转）
[例] 求一般面ABC的实形。
c f (h) n
点）、棱面CDHG的
V投影不可见；
e
m
b h1 (d) (d1)
§6-3 十换二面五法规的划应教用材例 7 ： 作 四 棱 柱 及 表 面 上 的 点 的 V 投 影
g1 (c1)
a
e1
f1 (b1)
(a1)
小结
十二五规划教材
小 结 — 求 线 面 与 投 影 面 的 倾 角
具体解题时,应将某个一般位置的直线或平面变换为特殊状态:
[例] 求线段的实长及倾角 。 （设立平面V1平行于线段AB，则新轴O1X1∥ab）
b1'
V
V1

换面法

换面法

换面法一、 换面法概述当直线或平面相对于投影面处于特殊位置（平行、垂直）时，它们的投影反映线段的实长、平面的实形及其与头面的倾角。

当直线或平面和投影面处于一般位置时，则它们的投影不具备上述特性。

换面法的目的，就在于将直线或平面从一般位置变换为和投影面平行或垂直的位置，以便于解决它们的度量和定位问题。

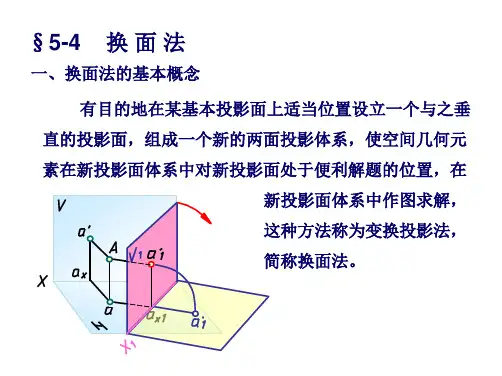
1．换面法的基本概念换面法就是保持空间几何元素不动，用一个新的投影面替换其中一个原来的投影面，使新投影面对于空间几何元素处于有利于解题的位置。

然后找出其在新投影面上的投影。

2．新投影面的选择原则（1）新投影面必须和空间的几何元素处于有利于解题的位置；（2）新投影面必须垂直于一个原有的投影面；（3）在新建立的投影体系中仍然采用正投影法。

二、 点的换面点是一切几何元素的基本元素。

因此在研究换面时，首先从点的投影变换来研究换面法的投影规律。

1．点的一次换面（1）换V 面图2-25（a ）表示点A 在原投影体系V/H 中，其投影为a 和a '现令H 面不动，用新投影面V 1来代替V 面，V 1面必须垂直于不动的H 面，这样便形成新的投影体系V 1/H ，O 1X 1是新投影轴。

过点A 向V 1面作垂线，得到V 1面上的新投影1a '，点1a '是新投影，点a '是旧投影，点a 是新、旧投影体系中的共有的不变投影。

a 和1a '是新的投影体系中的两个投影，将V 1面绕O 1X 1轴旋转到与H 面重合的位置时，就得到图2-25（b ）所示的投影图。

由于在（a ） （b ） （c ）图2-25点的一次变换（换V 面）新投影体系中，仍采用正投影方法，又在V/H 投影体系和V 1/H 体系中，具有公共的H 面，所以点a 到H 面的距离（Z 坐标）在两个题词体系中是相等的。

所以有如下关系： 1a 'a ⊥O 1X 1轴；1a '1x a =a 'x a =A a ，即：换V 面时Z 坐标不变。

水利类画法几何习题解答

水利类画法几何习题解答

19
(a)
(b)
(c)
(49)
(51)
*
6-9（18）
*
6-9（23）
空实关系的分析
P39
P39
P40
*
注意：已表达清楚的结构，其不 可见轮廓线不再画出
*
P40
*
*
注意：已表达清楚的结构，其不可见轮 廓线不再画出
* * *
*
注意： 1、已表达清楚的结构，其不可见轮廓线不再画出 2、剖切面前面的结构，轮廓线应删除 3、半个剖视图应画在右侧
形体分析法—— 切割法
(16)
(15)
形体分析法—— 切割法
形体分析法—— 切割法
6-9（11）
6-9（16）
6-9（27）
P72（13）
（）
P72（15）
已知主、俯视图求左视图 形体分析法—— 切割法
7-8(16)
已知主、左视图求俯视图
形体分析法—— 切割法
注意共面、面与 面的交线
P44
P45
* *
* **
*
注意标注
P46
P46
空空相贯、
实实相贯
P46
切点的确定
P41
P41
**
注意： 1、已表达清楚的结构，其不可见轮廓 线不再画出 2、剖切面前面的结构，轮廓线应删除 3、半个剖视图应画在右侧 4、空的部分不应画剖面线 5、剖切到的内部结构应画成粗实线
*
P42 * * * * * * * *
*
P43
*
*
*
注意： 1、已表达清楚的结构，其不可见轮廓线不再画出 2、剖切面前面的结构，轮廓线应删除，剖切面后面的可见轮廓线不可漏画。 3、半个剖视图应画在右侧 4、空的部分不应画剖面线 5、剖切到的内部结构应画成粗实线

画法几何及工程制图 天津大学离线考核题库及答案

画法几何及工程制图 天津大学离线考核题库及答案

画法几何及工程制图
请在以下五组题目中任选一组作答，满分100分。

第一组：
一、论述题（25分）
1.换面法的基本概念及原则。

答：换面法的基本概念：换面法就是保持空间几何元素不动，用一个新的投影面替换其中一个原来的投影面，使新投影面对于空间几何元素处于有利于解题的位置。

然后找出其在新投影面上的投影。

新投影面的选择原则：（1）新投影面必须和空间的几何元素处于有利于解题的位置；（2）新投影面必须垂直于一个原有的投影面；（3）在新建立的投影体系中仍然采用正投影法。

二、分析题（25分）
1.分析如何计算两交叉直线之间的距离。

答：采用换面法比较简单直观（1）对某一直线（如 l）经两次换面，使其成为垂线，投影集聚为点（如 m）（2）从 m 向另一直线 k 作垂线mn，mn即为两交叉直线 k , l 之间距离（真长）（3）如需求出两面投影，则按换面规则，反求出m，n投影即可
三、绘图题（每小题25分，共50分）
1. 补齐剖视图中所缺线条：。

8-换面法

8-换面法

n
c1 '
H
D X1 V1 a1 ' B
n1 ' m1 '
m2 b2
N
C
b1' V1 H2 距离实长 平行 X2
[例] 求二面角的夹角大小。 当二面交线垂直于新投影面时， 在新投影面上反映二面角实形。 a' C c' d' V X H b' c b 平行 a d d1 ' X1 H V1
A
K M θ N D
5. 投影面垂直面变换成新投影面平行面； 6. 一般面变换成新投影面平行面。
换面法的六个基本问题 求线段实长、倾角以及作垂直
（1）一般位置直线 → 投影面平行线
a’
V
b’
b’ a’ b
B
b1’
α a1’
A
X
V H
b
a a1’
X
α
b1’
a
X1
AB实长
（设立平面V1平行于线段AB， O1X1 ∥ab 则新轴O1X1∥ab）
c2
O1X1 ∥ ab
b1’
换面法的应用实例
[例］已知点 E 到直线 AB 的距离为20mm，求e’ 。
e’ b’
V X H
a’
e’ e b
经过两次变换使直线 AB 成为投影面垂直线后， 根据距离 20mm 可以确定 所求点的轨迹。
V1 H2
X2
l
l
a e1’ e2 b1’ e1’ a2 (b2) e2
求 两平面的夹 角 c’ a’ d’ 一般位置
X
求交叉两直线间 距 离
b’ c’
a’
X
b’ b a b’ a’ c

画法几何复习题

画法几何复习题

已知A点（10，10，15）；点B距离投影面H,V,W分别为20,15,20；点C在点A左方10，前方10，下方10，作出A、B、C的三面投影。

（10分）完成下列各点的第三面投影。

求出直线AB实长及直线与H面的倾角α，与Ｖ面的倾角β，与Ｗ面的倾角γ。

（9分）在直线AB上确定一点k，点k距H，V投影面等距（6分）。

用换面法求AB，CD间最短距离及其实长。

求直线AB对H、V面的倾角α、β及实长。

过C点作直线AB的垂线CD。

（两种方法）求平行两直线AB、CD间的距离。

用换面法求M点到ΔABC平面的距离MK的投影及实长。

用换面法求∠ABV的角平分线。

或作出立体（圆柱，圆锥，球）上点的三面投影根据所给的视图，补绘投影图。

求半球体被截切后的投影图。

补绘被截圆锥的另外两面投影分析圆柱的截交线，补全其三面投影。

（10分）求直立三棱柱与水平三棱柱的相贯线，并进行可见性的判定答案答案用换面法求△ABC 和△ABD 之间的夹角。

（12分）求切口三棱锥的H面和W面投影。

（12分）求作两轴线正交的圆柱体的相贯线。

补画园锥的投影2、下面四组过圆孔剖面图，画得正确的是( )一、选择题（12分）1、平面与圆球相交，截交线的空间形状是( C )。

A.椭圆B.双曲线C.圆D.直线2、侧垂面的H投影（ A ）。

A、呈类似形B、投影一直线C、反映平面对W 面的倾角D、反映平面对H面的倾角3、已知E点距H、V、W面的距离分为10、5、20；F点在E点上方5，左方10，前方15，由此可知F的坐标为（ B ）。

A、（15，30，35）B、（30，20，15）C、（15，20，30）D、（10，20，5）4、正垂面与侧垂面相交，其交线是（ C ）。

A、侧垂线B、水平线C、一般线D、正平线5、选择正确的三面投影图( A )。

（A）（B）（C）7、已知点A（0，10，25）和点B（0，15，25），关于点A和点B的相对位置，哪一种判断是正确的？（ D ）A、点A在点B前面B、点B在点A上方，且重影于V面上C、点A在点B前方，且重影在OZ轴上D、点B在点A前面8、正垂面的W投影（A ）。

换面法

换面法
AD C B adb P c X V H
c a
.
b d
. a1′ d1′
X1
距离
O2
如何确定 c1 ′ d1′点的位 V1 H2 X2 置？ 作线平行于O 过c1′作线平行于 2x2轴。
21
H O1 V 1
b1′. a2(b2)(d2) c2
例7、已知两交叉直线 和CD的公垂线的长度 为MN， 、已知两交叉直线AB和 的公垂线的长度 ， N 为水平线， 的投影。 且AB为水平线，求CD及MN的投影。 M 为水平线 及 的投影
作图： 作图：
● c′ ′
n′ ′ ●
●
●
d′ ′
空间及投影分析： 空间及投影分析：
当直线AB垂直于投影 当直线 垂直于投影 面时， 平行于投影面， 面时，MN平行于投影面， 平行于投影面 这时它的投影m1′ n1′ =MN, 这时它的投影 且m1′ n1′ ⊥c1′ d1′ 。 A X1
.
a′ ′ XV H a c
V3 V V V1 V V V2 V2 1 → → → →… 或者 → → → →… H H H2 H2 H H1 H1 H3
ห้องสมุดไป่ตู้
8
⑵ 求新投影的作图方法
a′ ′
作图规律
ax O X1 O2 ax2 . a1 ′ H2 V1 X 2
V X H
a2a1′ ⊥ O2X2 a2ax2 = aax1
a2
a ax1 H O1 V1
在平面上选择什么样的直线进行变换？ 在平面上选择什么样的直线进行变换？
在已知平面上所作的直线应是投影面平行线， 在已知平面上所作的直线应是投影面平行线， 而不应作一般位置直线。 而不应作一般位置直线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

画法几何题库之换面法
1.换面法求点D 到AB 直线的距离。

2.已知△ABC与△
ABD的夹角为90°,其交线
为AB,求△ABD的水平投影。

3.∠ABC＝30°,求AB的正面投影。

4.已知等边△ABC的一边BC在直线MN上，
高AD=30mm,
求作△ABC的两面投影。

(△ABC的a角
等于60°)
5 过点A作一正方形ABCD,其边BC在直线MN
上，求作正方形的两面投影。

6求交叉二直线AB和CD的公垂线及实长。

7.求△ABC绕AB轴转90°后的新投影,并分
析有几解
8直线AB
上一点C距点A为30mm，过点C作直
线AB的垂线，且与直线EF相交，求作该直线的两
面投影。

9.已知等边三角形ABC的C点在V面内，求
作此三角形的两面投影，问有几个答案若ab按箭头
方向平移，移至何处时，只有一个答案，再移动
时，情况如何
10在ABC内作直线DE，使它平行于BC边，且
相距15mm。

11已知平面四边形ABCD的点A在V面内，距H
面为25mm，试完成平面四边形的投影，若点A到H
面的距离不限，则点A应在什么地方
12求与二直线AB，AC等距的点的轨迹。

13求直线AB与平面的交点K,并判断可见性。

(1)
(2)
14已知BD为菱形的一对角线，顶点A在直线EF上，求菱形ABCD的投影。

15作一次换面，使交叉两直线AB及CD的投影面上的投影相互平行。

16求直线AB与△CDE的夹角
17在直线AB上找一点K，使它与△ MNC及△MND等距。

18求直线AB与月BC的夹角
19
20
21
22.
23
24
25
26。