画法几何_换面法
- 格式:ppt
- 大小:1.58 MB
- 文档页数:32

画法几何制图换面法画法几何制图是建筑、机械和电子等设计领域必备的技能。
它的一个重要部分就是“换面法”,它是通过将一个多面体拆分成多个简单的平面形状,然后再用这些形状来绘制其三维图形的方法。
本文将为你介绍如何运用换面法来画一个简单的多面体。
准备工作在开始绘制之前,需要准备以下工具:•笔和铅•直尺•三角尺•绘画纸步骤一:绘制立方体首先,我们要绘制一个基本的多面体,例如一个立方体。
为了做到这一点,我们可以绘制一个正方形(底面),并且在各个角上画上垂直于底面的线段(高),使这些线段接到正方形相应角点处,最后将所有线段相互连接即可形成一个立方体。
注意,在纵向和横向线段的描绘上,需要保持符合比例。
步骤二:拆分面以上述步骤绘制出来的立方体为例,我们需要将其所有的面分成矩形或正方形。
为此,我们需要通过连接每个相邻的面的棱角,将多面体拆解,并且用铅笔标上每个矩形或正方形的上下左右面,使得它们更加容易被识别。
步骤三:绘制每个面在拆分面后,我们可以将每个面单独绘制出来。
为此,我们需要将每个面放在纸上,并用三角尺和直尺来绘制它们。
对于不同的矩形,我们可以采用不同的绘制方法。
例如,对于一条平行于底面的直线,我们可以在每个与之相交的四边形上绘制这条直线,并保持符合比例。
在绘制完每个面后,我们应该标记好它们的相对位置。
步骤四:组成三维图形通过绘制每个面,我们可以将它们组合起来形成多面体的三维图形。
为此,我们应该将每个面按照它的相对位置粘贴到一张透明的塑料纸上,并对其进行调整,使得它们适当地重叠在一起。
这将帮助我们清晰地了解多面体的整体形状。
在这篇文章中,我们介绍了一个基本的画法几何制图技巧——换面法,以及如何使用这个技巧来画一个简单的多面体。
换面法可以帮助我们将多面体拆分成更简单的形状,并在绘制每个形状后重新组装它们来形成三维图形。
这个技巧在建筑、机械和电子等领域的设计工作中都得到了广泛应用。


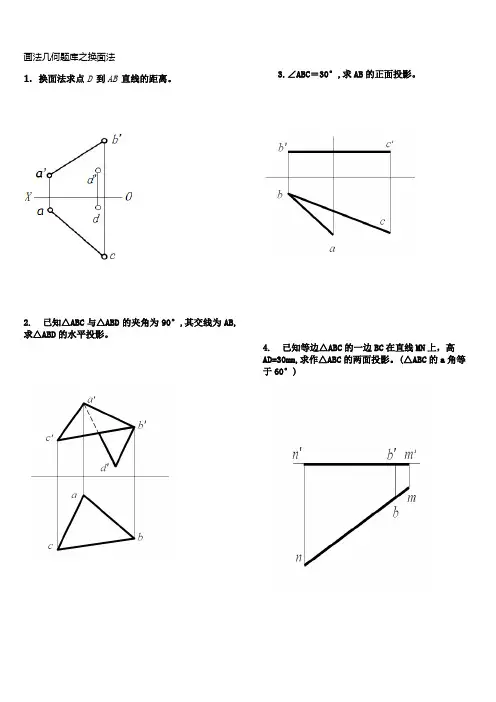
画法几何题库之换面法1.换面法求点D 到AB 直线的距离。
2.已知△ABC与△ABD的夹角为90°,其交线为AB,求△ABD的水平投影。
3.∠ABC=30°,求AB的正面投影。
4.已知等边△ABC的一边BC在直线MN上,高AD=30mm,求作△ABC的两面投影。
(△ABC的a角等于60°)5 过点A作一正方形ABCD,其边BC在直线MN上,求作正方形的两面投影。
6求交叉二直线AB和CD的公垂线及实长。
7.求△ABC绕AB轴转90°后的新投影,并分析有几解?8直线AB 上一点C距点A为30mm,过点C作直线AB的垂线,且与直线EF相交,求作该直线的两面投影。
9.已知等边三角形ABC的C点在V面内,求作此三角形的两面投影,问有几个答案?若ab按箭头方向平移,移至何处时,只有一个答案,再移动时,情况如何?10在ABC内作直线DE,使它平行于BC边,且相距15mm。
11已知平面四边形ABCD的点A在V面内,距H面为25mm,试完成平面四边形的投影,若点A到H面的距离不限,则点A应在什么地方?12求与二直线AB,AC等距的点的轨迹。
13求直线AB与平面的交点K,并判断可见性。
(1)(2)14已知BD为菱形的一对角线,顶点A在直线EF上,求菱形ABCD的投影。
15作一次换面,使交叉两直线AB及CD的投影面上的投影相互平行。
16求直线AB与△CDE的夹角17在直线AB上找一点K,使它与△ MNC及△MND等距。
18求直线AB与月BC的夹角19 202122.2324 2526(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。




广东技术师范学院天河学院教案2012 年月日第周单元教案首页第三章投影变换——换面法第一节换面法的基本概念一、换面法的基本概念空间几何元素的位置保持不变,用新的投影面来代替旧的投影面,使空间几何元素对新的投影面的相对位置变成有利于解题的位置,然后找出其在新投影面上的投影。
这种方法称为换面法。
用换面解题时应遵循下列两原则:⒈选择新投影面时,应使几何元素处于有利于解题的位置;⒉新投影面必须垂直于原投影面体系中不被变换的投影面,并与它组成新投影面体系,必要时可连续变换。
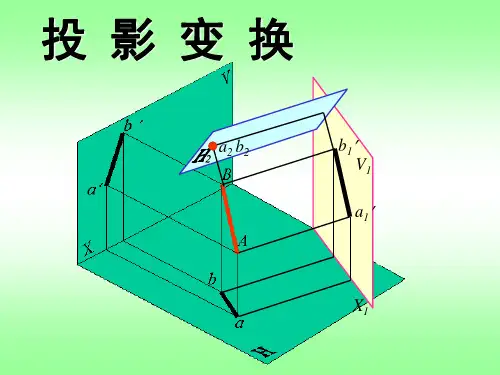
(a) (b)图3.1 将一般位置直线变换成投影面平行线如图3.1,新投影面必须垂直于不变换的投影面,即V1⊥H,X1为新投影轴。
这时,不变换投影面上的投影a、b与V1面上的新投影a1'、b1'的投影连线a a1'⊥X1、b b1'⊥X1。
并且a1'、b1'到X1的距离等于被代替的投影a'、b'到被代替的投影轴的距离,即a1'a X1=a'a X=A a=Z A, b1'b X1=b'b X=B b=Z B。
第二节点的换面二、点的投影变换规律(一)点的一次变换点是一切几何形体的基本元素。
因此,必须首先掌握点的投影变换规律。
现在来研究更换正立投影面时,点的投影变换规律。
图3表示点A在V/H 体系中,正面投影为a′,水平投影为a。
现在令H面不变,取一铅垂面V1(V1⊥H)来代替正立投影面V,形成新投影面体系V1/H。
将点A向V1投影面投射,得到新投影面上的投影a′1。
这样,点A在新、旧两体系中的投影(a,a′1)和(a,a′)都为已知。
其中a′1为新投影,a′为旧投影,而a为新、旧体系中共有的不变投影。
它们之间有下列关系:1. 由于这两个体系具有公共的水平面H,因此点A到H面的距离(即z坐标),在新旧体系中都是相同的,即a′ax=Aa=a′1ax1。
2. 当V1面绕X1轴重合到H面时,根据点的投影规律可知aa′1必定垂直于X1轴。
这和aa′⊥X轴的性质是一样的。
画法几何及工程制图
请在以下五组题目中任选一组作答,满分100分。
第一组:
一、论述题(25分)
1.换面法的基本概念及原则。
答:换面法的基本概念:换面法就是保持空间几何元素不动,用一个新的投影面替换其中一个原来的投影面,使新投影面对于空间几何元素处于有利于解题的位置。
然后找出其在新投影面上的投影。
新投影面的选择原则:(1)新投影面必须和空间的几何元素处于有利于解题的位置;(2)新投影面必须垂直于一个原有的投影面;(3)在新建立的投影体系中仍然采用正投影法。
二、分析题(25分)
1.分析如何计算两交叉直线之间的距离。
答:采用换面法比较简单直观(1)对某一直线(如 l)经两次换面,使其成为垂线,投影集聚为点(如 m)(2)从 m 向另一直线 k 作垂线mn,mn即为两交叉直线 k , l 之间距离(真长)(3)如需求出两面投影,则按换面规则,反求出m,n投影即可
三、绘图题(每小题25分,共50分)
1. 补齐剖视图中所缺线条:。