吊钩强度计算

◆吊钩横梁计算一、已知设计参数图1 吊钩横梁Q=2500000Nd=284mml=723mmh=278mmB=600mm材料：45屈服强度：355Mpa二、中间截面A-A的最大弯曲应力σ=MW=1.5Ql(B−d)h2=1.5∗2500000∗723 (600−284)∗278∗278=112≤3552.5=142Mpa起重机设计手册P252公式3-4-12结论：计算通过;◆拉板计算一、已知设计参数图2 拉板Q=2500000Nh01=641mmh02=340mmb=650mmδ1=92mmδ2=92mmd1=220mmd2=240mm上部轭板的应力集中系数αj1=下部轭板的应力集中系数αj2=材料：Q235A屈服强度：235Mpa二、上部拉板计算水平截面A－A的内侧孔边最大拉应力σt＝Qαj12(b−d1)δ1＝2500000∗2.32 2∗(650−220)∗92=74≤2351.7=138Mpa起重机设计手册P253公式3-4-15结论：计算通过;垂直截面B－B的内侧孔边最大拉应力σ＝Q(h012+0.25d12) 2d1δ1(h012−0.25d12)＝2500000∗(6412+0.25∗2202) 2∗220∗92∗(6412−0.25∗2202)=66≤2353=78Mpa起重机设计手册P253公式3-4-16结论：计算通过;轴孔d1处的平均挤压应力许用挤压应力[σbs]的取值：按工作时无相对转动进行取值,中小起重量≤100t取值为σs 4,大起重量>100t取值为σs3;σbs=Q2d1δ1=2500000 2∗220∗92=62≤2353=78Mpa起重机设计手册P253公式3-4-17结论：计算通过;三、下部拉板计算水平截面C－C的内侧孔边最大拉应力σt＝Qαj22(b−d2)δ2＝2500000∗2.28 2∗(650−240)∗92=76≤2351.7=138Mpa起重机设计手册P253公式3-4-15结论：计算通过;垂直截面D－D的内侧孔边最大拉应力σ＝Q(h022+0.25d22) 2d2δ2(h022−0.25d22)＝2500000∗(3402+0.25∗2402) 2∗240∗92∗(3402−0.25∗2402)=73≤2353=78Mpa起重机设计手册P253公式3-4-16结论：计算通过;轴孔d2处的平均挤压应力许用挤压应力[σbs]的取值：按工作时无相对转动进行取值,中小起重量≤100t取值为σs 4,大起重量>100t取值为σs3;σbs=Q2d2δ2=25000002∗240∗92=57≤2353=78Mpa起重机设计手册P253公式3-4-17结论：计算通过;◆滑轮轴计算一、已知设计参数图3 滑轮轴计算简图中间滑轮数量n1=4两侧滑轮数量n2=3拉板两侧相邻滑轮中心线之间的距离l2=258mm其他区域相邻滑轮中心线之间的距离l1=155mm中间滑轮之间距离的总和L=465mm滑轮钢丝绳拉力的合力S=250000N轴径：220mm材料：40Cr调质屈服强度：490Mpa二、最大剪应力计算滑轮轴所受剪力的两个极值均在支点处,分别用F1、F2表示;在求最大剪应力时,应选择F1、F2中绝对值较大者进行计算;F1=n2S=3250000=750000NF2=-R-n2S==4250000=-500000Nτmax=4F max πd2=4∗750000π∗2202=20≤113Mpa 结论：计算通过; 三、最大弯曲正应力计算滑轮轴所受弯矩的两个极值在支点处和中心处,分别用M 1、M 2表示;在求最大弯曲正应力时,应选择M 1、M 2中绝对值较大者进行计算;M1=−(n 2∗l 22+n 2(n 2−1)2l 1)S =−(3∗2582+3∗(3−1)2∗155)∗250000=Nmm中心处弯矩M 2等于右侧滑轮对中心处的弯矩M 右、支反力对中心处的弯矩M 支、中间滑轮对中心处的弯矩M 中之和,即M 2=M 右+M 支+M 中;M 右=−(n 2∗l 22+n 2(n 2−1)2l 1)S −(L 2+l 22)∗S ∗n 2 =−(3∗2582+3∗(3−1)2∗155)∗250000−(4652+2582)∗250000∗3 =NmmM 支=(0.5n1+n2)S ∗(L 2+l 22)=(0.5∗4+3)∗250000∗(4652+2582)=NmmM 中=−int(n 1+12)(int(n 1+12)−1)2∗l 1∗S=−int (4+12)∗(int(4+12)−1)2∗155∗250000=NmmM 中=−int(n 1+12)(int(n 1+12)−1)2∗l 1∗S −int(n 1+12)∗l 12∗S=−int (4+12)∗(int(4+12)−1)2∗155∗250000−int(4+12)∗1552∗250000=NmmM 2=M 右+M 支+M 中=+ =Nmmσmax =M max W=M maxπd 332 =π∗220332=204>4902.5=196Mpa起重机设计手册P252公式3-4-14 结论：计算不通过;。

电梯梁吊钩计算公式电梯梁是一种用于吊装货物或设备的重要工具，而吊钩则是电梯梁上的关键部件之一。

吊钩的设计和计算是非常重要的，因为它直接关系到吊装的安全性和稳定性。

在本文中，我们将讨论电梯梁吊钩的计算公式，以及一些相关的注意事项。

首先，让我们来看一下电梯梁吊钩的基本结构。

一般来说，电梯梁吊钩由吊钩本体、吊钩轴、吊钩销和吊钩螺栓等部件组成。

吊钩本体是吊钩的主要部分，它承担着承载货物或设备的重量。

吊钩轴是连接吊钩本体和电梯梁的部件，它需要具有足够的强度和刚度来承受吊装过程中的各种力学作用。

吊钩销和吊钩螺栓则用于连接吊钩本体和吊钩轴，它们也需要具有足够的强度和可靠性。

在进行电梯梁吊钩的计算时，我们需要考虑吊钩在吊装过程中所受到的各种力学作用，包括静载、动载和冲击载荷等。

根据这些力学作用，我们可以得到电梯梁吊钩的计算公式。

首先，我们来看一下静载情况下的计算公式。

在静载情况下，吊钩所受到的主要力学作用是重力和静载荷。

根据力学原理，我们可以得到以下的计算公式：N = P + F。

其中，N为吊钩的受力情况，P为货物或设备的重力，F为静载荷。

根据这个公式，我们可以计算出吊钩在静载情况下的受力情况，从而选择合适的吊钩材料和尺寸。

接下来，我们来看一下动载情况下的计算公式。

在动载情况下，吊钩所受到的主要力学作用是动载荷和惯性力。

根据力学原理，我们可以得到以下的计算公式：N = P + F + I。

其中，N为吊钩的受力情况，P为货物或设备的重力，F为动载荷，I为惯性力。

根据这个公式，我们可以计算出吊钩在动载情况下的受力情况，从而选择合适的吊钩材料和尺寸。

最后，我们来看一下冲击载荷下的计算公式。

在冲击载荷下，吊钩所受到的主要力学作用是冲击载荷和惯性力。

根据力学原理，我们可以得到以下的计算公式：N = P + F + I。

其中，N为吊钩的受力情况，P为货物或设备的重力，F为冲击载荷，I为惯性力。

根据这个公式，我们可以计算出吊钩在冲击载荷下的受力情况，从而选择合适的吊钩材料和尺寸。

结构吊装计算
一、吊钩计算
依据<<建筑施工计算手册>>,<<建筑结构荷载规范>>GB50009-2001,<<建筑材料规范大全>>, <<钢结构设计规范>>GB50017-2003。

现对吊钩纯受力时验算。

8.3 钢屋架吊装计算
1、吊索规格的选择
Q
屋面梁1118.08kg,钢柱1713.625 kg。

屋架垂直吊起后，按力的平衡条件吊索中垂直分力之和应等于屋架的重力。

则吊索的内力；Pg= G/sina=10.96/sin45=7.77KN
吊索取6×37，换算系数取0.82，安全系数取K=8。

钢丝绳破断拉力总和：Fg=8×7.77/0.82=75.84KN
选用抗拉强度为1400N/㎜²、ф15㎜的钢丝绳，Pg=119.5KN>75.84KN，满足要求。

3、起重机起重高度的确定
起重机的起重高度可通过下式计算：H≧h1+h2+h3+h4
H——为起重机的起重高度；
h1——安装支座表面高度，为2m；
h2——安装间隙，取0.3m；
h3——钢屋架高度，为14.15m；
h4——屋架到吊钩距离，取4m；
在吊装1`3轴钢屋架时，汽车起重机臂长
=20.45/sin70=21.76m
L≥H
SINA
则吊车的工作幅度为21.76*cos70=7.44米。

吊车主臂长21.76m，吊起的最大起重量为18KN，所以选择 QZ16型徐州，臂长23.5米。

300t吊钩组计算书一、吊钩(图号：SA90C1a-6)计算参照机械设计手册第二卷第8篇P8-112页采用钩号250-P的尺寸以下计算公式参照起重机设计手册P248页。

1.钩孔直径双钩实际钩孔2.其它尺寸，实际实，实际实，实际实3.锻造吊钩强度计算(材质DG20Mn)双钩钩身钩身垂直截面B-B和倾斜截面C-C是危险截面。

①截面B-B中，内侧最大拉应力：内②截面C-C中，内侧最大拉应力：③头部直柄直柄钩颈最小截面拉应力：螺纹的剪应力τ按第一圈螺纹承受有效载荷的一半、剪切面的高度为螺距的一半的假定计算：内二、吊钩横梁(图号：SA90C1a-5)计算以下计算公式参照起重机设计手册P252页 (材质DG20Mn)。

1.中间截面A-A 的最大弯曲应力：2.轴孔的d1的平均挤压应力：(建议贴板改 )三、滑轮轴(图号：SA90C1a-10)计算(材质42CrMo) 以下计算公式参照起重机设计手册P252页根据拉板在滑轮轴上的不同位置，作出滑轮轴不同的弯矩图， 最大弯曲应力：(建议采用材质42Cr)钢丝绳最大拉力：滑轮水平作用力： 四、轭板(图号：SA90C1a1)计算拉板上有轴孔的水平截面A-A 和垂直截面B-B 为危险截面(材质Q345-B)。

水平截面A-A 的内侧孔边最大拉应力为：垂直截面B-B 的内侧孔边最大拉应力(切向)：轴孔处的平均挤压应力：五、滑轮(图号:WJ6251)计算参照机械设计手册第二卷第8篇P8-93页E 型滑轮尺寸以下计算公式参照机械设计手册第二卷第8篇P8-85页(材质Q235-B)。

轮缘最大弯曲应力： 单辐条内压应力：单钢丝绳最大拉力： 单六、吊钩推力轴承计算轴承采用标准号：GB/T5859 轴承代号：29368 外形尺寸：φ340×540×122以下计算公式参照机械设计手册第二卷第7篇P7-237页。

时，轴向当量静载荷：吊钩额定静载荷：七、滑轮轴承计算轴承采用标准号：GB/T283 轴承代号：NJ232 外形尺寸：φ160×290×48以下计算公式参照机械设计手册第二卷第7篇P7-232页。

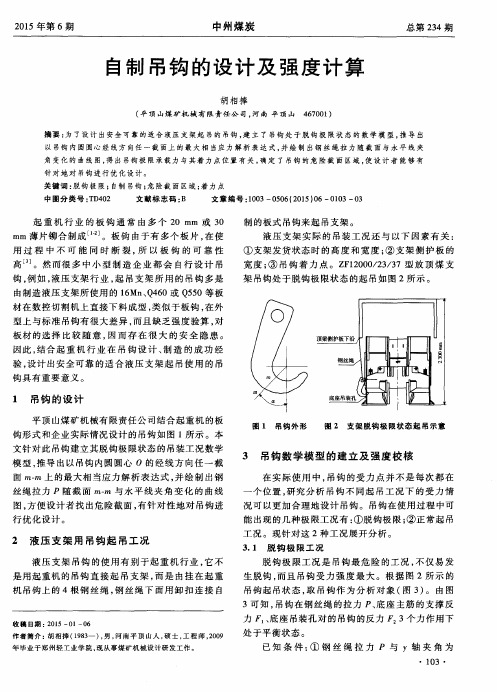
自制普通钢材钢板吊钩（A、B型）外形尺寸及受力计算编制：徐勇德审核：日期：2011年9月19日1A型自制普通钢材钢板吊钩外形尺寸及允许负载计算：外形尺寸附图：A型允许负载计算：G屈服点为235N/mm²(24Kgf/ mm²)的钢材塑性材料的安全系数n，在机械设计中一般取n=1.5～2.5。

我们在这里取中间值n=2。

C—不均匀受力系数取1.5～2.0，我们在这里取C=2。

安装系数：S=5。

抗拉强度：P=24Kgf×(120×20×+120×10)=86400Kgf。

吊钩的允许荷载:实际吊装允许负载=G÷S=21600÷5≈4300Kg。

得：实际吊装允许负载为4300Kg。

23B型自制普通钢材钢板吊钩外形尺寸及允许负载计算：外形尺寸附图：B型允许负载计算：G屈服点为235N/mm²(24Kgf/ mm²)的钢材塑性材料的安全系数n，在机械设计中一般取n=1.5～2.5。

我们在这里取中间值n=2。

C—不均匀受力系数取1.5～2.0，我们在这里取C=2。

安装系数：S=5。

横截面面积：A=(40×20)×2=1600mm²吊钩的允许荷载 :。

得：吊钩的允许荷载为3840Kg/f。

焊缝抗拉强度及允许拉力计算：焊缝：120×5+120×5+150×5+150×5=2700mm²屈服点为235N/mm²(24Kgf/ mm²)的钢材焊缝抗拉强度：P=24Kgf×2700mm²=64800Kg。

吊钩的允许荷载 : 。

得：实际吊装允许负载为3240Kg。

4。

吊钩的抗拉强度计算公式引言。

在工程施工中，吊钩是一种常用的起重工具，用于吊装各种重物。

吊钩的抗拉强度是指吊钩在受力状态下所能承受的最大拉力，是保证吊钩安全使用的重要参数。

本文将介绍吊钩的抗拉强度计算公式，以及相关的计算方法和注意事项。

吊钩的抗拉强度计算公式。

吊钩的抗拉强度计算公式可以通过以下公式进行计算：F = A ×σ。

其中，F为吊钩的抗拉强度，单位为牛顿（N）；A为吊钩的横截面积，单位为平方米（m²）；σ为吊钩的材料抗拉强度，单位为帕斯卡（Pa）或兆帕（MPa）。

吊钩的横截面积A可以根据吊钩的形状和尺寸进行计算，常见的吊钩形状包括圆形、方形、矩形等，可以根据实际情况选择相应的计算方法。

吊钩的材料抗拉强度σ是指吊钩材料在受拉状态下所能承受的最大拉力，是由吊钩的材料性能和工艺制造水平决定的。

通常情况下，吊钩的材料抗拉强度可以在相关标准或技术规范中查找到。

吊钩的抗拉强度计算方法。

在实际工程中，吊钩的抗拉强度可以通过以下步骤进行计算：1.确定吊钩的形状和尺寸，计算吊钩的横截面积A；2.查找吊钩材料的抗拉强度σ；3.将吊钩的横截面积A和材料抗拉强度σ代入计算公式F = A ×σ中，进行计算得出吊钩的抗拉强度F。

需要注意的是，吊钩的抗拉强度计算中还需要考虑吊钩的使用环境和工作条件，例如吊钩的受力方向、受力大小、使用温度等因素，这些因素都会对吊钩的抗拉强度产生影响，需要在计算中进行综合考虑。

吊钩的抗拉强度计算注意事项。

在进行吊钩的抗拉强度计算时，需要注意以下几点：1.选择合适的计算方法，根据吊钩的形状和尺寸选择相应的计算方法，确保计算结果准确可靠；2.准确获取材料抗拉强度，查找吊钩材料的抗拉强度时，要确保获取的数据准确可靠，避免因材料抗拉强度数据不准确导致计算结果出现偏差；3.综合考虑使用环境和工作条件，在计算吊钩的抗拉强度时，需要综合考虑吊钩的使用环境和工作条件，确保计算结果符合实际情况。

吊装方案吊具吊索计算公式咱来说说吊装方案里吊具吊索计算公式那些事儿。

一、钢丝绳（吊索）拉力计算。

1. 单根钢丝绳垂直吊装。

要是你就用一根钢丝绳垂直吊一个物体，那这根钢丝绳受到的拉力就等于物体的重力。

公式就是F = G，这里的F是钢丝绳的拉力，G是物体的重力。

重力咋算呢？G = mg，m是物体的质量（单位是千克），g是重力加速度，大概是9.8牛/千克（在粗略计算的时候也可以取10牛/千克）。

比如说，你要吊一个100千克的东西，那它的重力G = 100×9.8 = 980牛，那这根钢丝绳的拉力F也就是980牛。

2. 多根钢丝绳垂直吊装且均匀受力。

假如你用n根钢丝绳垂直吊一个物体，而且每根钢丝绳均匀受力的话，那每根钢丝绳受到的拉力就等于物体重力除以钢丝绳的根数。

公式就是F=(G)/(n)。

就好比你用4根钢丝绳吊一个4000牛的东西，那每根钢丝绳的拉力F=(4000)/(4)=1000牛。

3. 倾斜吊装（单根钢丝绳）当钢丝绳倾斜吊装物体的时候，情况就有点复杂了。

这时候钢丝绳的拉力可就不等于物体的重力了。

我们得用三角函数来算。

如果钢丝绳和垂直方向的夹角是θ，那钢丝绳的拉力F=(G)/(cosθ)。

比如说，你吊一个1000牛的东西，钢丝绳和垂直方向夹角是30度，那cos30^∘=(√(3))/(2)，这根钢丝绳的拉力F=(1000)/(frac{√(3)){2}}≈1155牛。

二、吊具（吊钩等）的受力计算。

1. 简单吊钩垂直受力。

对于吊钩来说，如果是垂直吊装，它受到的力就是物体的重力。

和前面单根钢丝绳垂直吊装时钢丝绳拉力计算一样，F = G。

2. 多个吊点通过吊具吊装。

要是有多个吊点通过一个吊具吊装物体，那这个吊具受到的合力还是等于物体的重力。

但是呢，在考虑吊具的强度等问题时，你得分析每个吊点对吊具的分力。

这时候就又得用到三角函数啦。

假如有两个吊点，它们和水平方向的夹角分别是α和β，物体重力是G，那这两个吊点对吊具的分力F_1和F_2可以根据力的分解来计算。

结构吊装计算一、吊钩计算依据〈<建筑施工计算手册>〉，<<建筑结构荷载规范〉〉GB50009-2001,〈<建筑材料规范大全〉〉， <<钢结构设计规范〉〉GB50017—2003。

现对吊钩纯受力时验算。

1、吊钩螺杆部分截面验算:吊钩螺杆部分可按受拉构件由下式计算：式中: t──吊钩螺杆部分的拉应力；F──吊钩所承担的起重力，取 F=10000。

00N（纯受力）; A1──螺杆扣除螺纹后的净截面面积:其中 d1──螺杆扣除螺纹后的螺杆直径（mm)，取d1=20.00mm;[σt］──钢材容许受拉应力。

经计算得：螺杆扣除螺纹后的净截面面积 A1=3.14×20.002/4=314。

16mm2；螺杆部分的拉应力σt=10000.00/314.16=31。

83N/mm2。

由于吊钩螺杆部分的拉应力31.83（N/mm2）,不大于容许受拉应力50.00（N/mm2),所以满足要求！2、吊钩水平截面验算:水平截面受到偏心荷载的作用，在截面内侧的K点产生最大拉应力σc,可按下式计算:式中： F──吊钩所承担的起重力，取 F=10000.00N;A2──验算2-2截面的截面积,其中： h──截面高度，取 h=38.00mm；b1，b2──分别为截面长边和短边的宽度，取 b1=30。

00mm，b2=25。

00mm； Mx──在2—2截面所产生的弯矩，其中： D──吊钩的弯曲部分内圆的直径（mm），取 D=35。

00mm；e1──梯形截面重心到截面内侧长边的距离，λx──截面塑性发展系数，取λx=1.00;W x──截面对x-x轴的抵抗矩,其中： I x──水平梯形截面的惯性矩,[σc]──钢材容许受压应力,取 [σc］=70.00N/mm2;2—2截面的截面积 A2=38。

00×（30.00+25。

00）/2=1045.00mm2；解得：梯形截面重心到截面内侧长边的距离 e1=18。

武汉交通职业学院港口起重机械课程设计设计题目：桥式起重机吊钩设计计算专业：轮机工程技术（港口）班级：学号：姓名：指导教师：日期：2011年11月25日目录第1章设计概述 (3)1.1设计主要内容 (3)1.2设计主要思路 (3)1.3设计背景和意义 (3)第2章吊钩的设计 (4)2.1吊钩装置概述 (4)2.2设计计算过程 (4)2.3计算方法概述 (4)2.4主要技术指标: (4)2.5吊钩原始参数及概述 (5)2.6吊钩设计步骤 (5)2.7钩身校核: (6)第3章吊钩横梁计算: (7)第3章拉板计算: ........................................................................ 错误！未定义书签。

第4章滑轮选择计算 (8)4.1滑轮直径的确定： (8)4.2滑轮轴受力图、弯矩图 (8)4.3滑轮轴计算: (8)第5章钢丝绳 ............................................................................. 错误！未定义书签。

第6章卷筒设计与校核 ............................................................. 错误！未定义书签。

6.1卷筒的设计 ................................................................... 错误！未定义书签。

6.2卷筒的强度校核及抗压稳定性验算 ........................... 错误！未定义书签。

6.3卷筒计算及校核 ........................................................... 错误！未定义书签。

设计心得...................................................................................... 错误！未定义书签。