2011g3wsyl008 第八讲 空间几何体

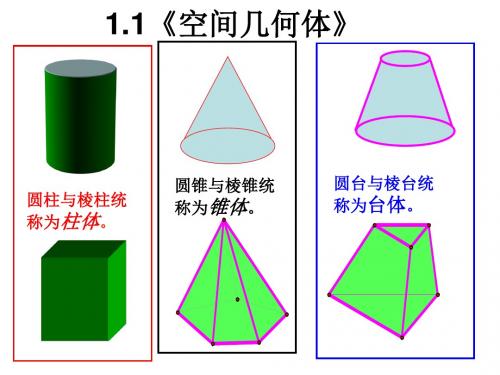
第一章空间几何体1.1 空间几何体的结构1. 多面体与旋转体：（1）由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面.相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点.（2）由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体，叫做旋转体，这条定直线叫做旋转体的轴.2. 棱柱：（1）有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱.棱柱中，两个互相平行的面叫做棱柱的底面（简称底），其余各面叫做棱柱的侧面，相邻侧面的公共边叫做棱柱的侧棱，侧面与底面的公共顶点叫做棱柱的顶点.（2）侧棱垂直于底面的棱柱叫直棱柱，否则斜棱柱；底面是正多边形的直棱柱叫正棱柱。

（3）棱柱的分类：按底面的多边形的边数分，有三棱柱、四棱柱、五棱柱等.按侧棱与底面的关系分为直棱柱和斜棱柱。

（4）底面是平行四边形的四棱柱叫平行六面体；侧棱与底面垂直的平行六面体叫直平行六面体；底面为矩形的直平行六面体叫长方体；底面为正方形的长方体叫正四棱柱；棱长都相等的正四棱柱叫正方体。

（5）棱柱的性质：①两底面是对应边平行的全等多边形；②侧面、对角面都是平行四边形；③侧棱平行且相等；④平行于底面的截面是与底面全等的多边形。

3. 棱锥：（1）有一个面是多边形，其余各面都是有一公共点的三角形，由这些面所围成的几何体叫做棱锥.棱锥中，这个多边形面叫做棱锥的底面或底，有公共顶点的各个三角形面叫做棱锥的侧面，各侧面的公共顶点叫做棱锥的顶点，相邻侧面的公共边叫做棱锥的侧棱.（2）底面是正多边形，顶点在底面的射影是正多边形的中心的棱锥叫正棱柱。

正棱柱顶点与底面中心的连线段叫正棱锥的高；正棱锥侧面等腰三角形底边上的高叫正棱锥的斜高。

（3）棱锥的分类：按底面的多边形的边数分，有三棱锥、四棱锥、五棱锥等.（4）棱锥的性质：①侧面、对角面都是三角形；②平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方.（5）正棱锥的性质：①正棱锥各侧棱都相等，各侧面都是全等的等腰三角形。

§8.1空间几何体的结构要点梳理1.多面体：一般地，由若干个平面多边形围成的几何体叫做多面体。

构成：顶点、棱、面按面分类：四面体、五面体、六面体、……，一个多面体最少有4个面。

(1)棱柱定义：两个平面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面围成的多面体称为棱柱.构成：底面、侧面、侧棱、顶点表示法：用表示底面各顶点的字母表示棱柱分类1：按底面多边形的边数分为三棱柱、四棱柱、五棱柱……分类2：直棱柱、斜棱柱、平行六面体、正棱柱。

结构特征：上下底面平行，侧棱都平行且相等，上底面和下底面是全等的多边形. 截面等。

(2)棱锥定义：有一面为多边形，其余各面都是有一个公共顶点的三角形，这些面围成的多面体叫做棱锥.构成：底面（底）、侧面、侧棱、顶点.表示法：用顶点和底面各顶点的字母表示.分类1：按底面多边形的边数分为三棱锥、四棱锥、五棱锥……分类2：斜棱锥、正棱锥。

结构特征：底面是任意多边形，侧面是有一个相交与的三角形. 截面等。

(3)棱台定义：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫做棱台.构成：上下底面、侧面、侧棱、顶点.表示法：用顶点和底面各顶点的字母表示.分类1：按底面多边形的边数分为三棱台、四棱台、五棱台……分类2：斜棱台、正棱台。

结构特征：上下底面的两个多边形平行且相似. 截面等。

2.旋转体：由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体，这条定直线叫做旋转体的轴.(1)圆柱定义：以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的旋转体叫做圆柱. 旋转轴叫做圆柱的轴。

构成：上下底面、侧面、母线。

表示：表示轴的字母表示规定：圆住和棱住统称为住体.结构特征：上下底面平行且全等的圆，母线平行且相等，侧面展开图是矩形，轴截面是矩形，截面等。

(2)圆锥定义：以直角三角形的一条直角边所在的直线为旋转轴，其余两边旋转而形成的面所围成的旋转体叫做圆锥.旋转轴叫做圆锥的轴。

2.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )．注意：(1)空间几何体的三视图是该几何体在三个两两垂直的平面上的正投影，并不是从三个方向看到的该几何体的侧面表示的图形．(2)在画三视图时，重叠的线只画一条，能看见的轮廓线和棱用实线表示，挡住的线要画成虚线．知识点3：空间几何体的直观图3.已知正三角形ABC的边长为a，那么△ABC的平面直观图△Ａ＇Ｂ＇Ｃ＇的面积为( )．A.34a2 B.38a2C.68a2D.616a2注意:直接根据水平放置的平面图形的直观图的斜二测画法规则即可得到平面图形的面积是其直观图面积的22倍，这是一个较常用的重要结论．知识点4：几何体的表面积4.一个空间几何体的三视图如图所示，则该几何体的表面积为( )．A．48 B．32＋817C．48＋817 D．80注意：以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．知识点5：几何体的体积5.某几何体的三视图如图所示,它的体积为（ ）A ．B ．C ．D ． 注意：以三视图为载体考查几何体的体积，解题的关键是根据三视图想象原几何体的形状构成，并从三视图中发现几何体中各元素间的位置关系及数量关系，然后在直观图中求解．知识点6：空间与平面的转化6.已知在直三棱柱ABCA 1B 1C 1中，底面为直角三角形，∠ACB ＝90°，AC ＝6，BC ＝CC 1＝2，P 是BC 1上一动点，如图所示，则CP ＋PA 1的最小值为________．注意：研究几何体表面上两点的最短距离问题，常选择恰当的母线或棱展开，转化为平面上两点间的最短距离问题．★综合题训练7.已知某几何体的俯视图是如右图所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．(1)求该几何体的体积V ；(2)求该几何体的侧面积S .12π45π57π81π8.如图，已知某几何体的三视图如下(单位：cm)．(1)画出这个几何体的直观图(不要求写画法)；(2)求这个几何体的表面积及体积．9.如图，多面体ABFEDC的直观图及三视图如图所示，M，N分别为AF，BC的中点．(1)求证：MN∥平面CDEF；(2)求多面体A—CDEF的体积．赠送以下学习资料和倍差倍问题学习目标通过和倍、差倍问题的学习，除了掌握这类问题的解决方法以外，其重点要学习画线段图。