下载文档原格式
弯矩二次分配法计算步骤弯矩二次分配法是一种常用于计算梁受力的方法。
它基于弹性理论，以两层计算来估算梁上的弯曲应力，具有比较精确的计算结果。
本文将为您详细介绍弯矩二次分配法的计算步骤。
1. 确定梁上的荷载和支座反力在进行弯矩二次分配计算之前，首先需要确定梁上的荷载和支座反力。
荷载涵盖集中荷载、均布荷载和分布荷载等多种类型。
支座反力是指支撑梁的支座所产生的反力。
这些参数都需要明确，才能进行后续的计算。
2. 拟设约束条件和位移函数其次，需要拟设约束条件和位移函数。
在计算弯矩时，梁的基本自由度是两个，即梁端的转角和弯曲变形。
因此，需要通过设定约束条件来限制这两个自由度。
同时，还需要拟设一些位移函数，来近似描述梁的实际弯曲变形。
3. 计算一次弯矩分布接下来，进行一次弯矩分布计算。
这一步的目的是计算出梁在受力时的一次弯曲变形。
该过程需要先求出梁上的切线角和弧长，进而推导出弯矩斜率。
最后，通过积分计算得到一次弯矩分布。
4. 计算反向弯矩分布在得到一次弯矩之后，需要计算反向弯矩。
该过程涉及到两个步骤。
首先，要将约束条件带入到反向弯矩分布的位移函数中，对其进行求导以求得反向弯矩的斜率。
其次，通过积分计算出反向弯矩的分布函数。
5. 计算二次弯矩分布利用一次弯矩和反向弯矩之间的关系，可以得到二次弯矩的分布。
具体而言，二次弯矩的分布函数等于一次弯矩分布函数加上反向弯矩分布函数，再除以两次微分运算得到的分母项。
6. 计算合成弯矩分布最后，通过一次弯矩和二次弯矩的叠加，计算出梁上的合成弯矩分布。
该过程可以简化为一次弯矩加上一半的二次弯矩，来得到更加准确的计算结果。
总的来说，弯矩二次分配法的计算步骤相对复杂，需要多次迭代计算。
但该方法计算结果相对精确，可以在工程实践中得到广泛应用。
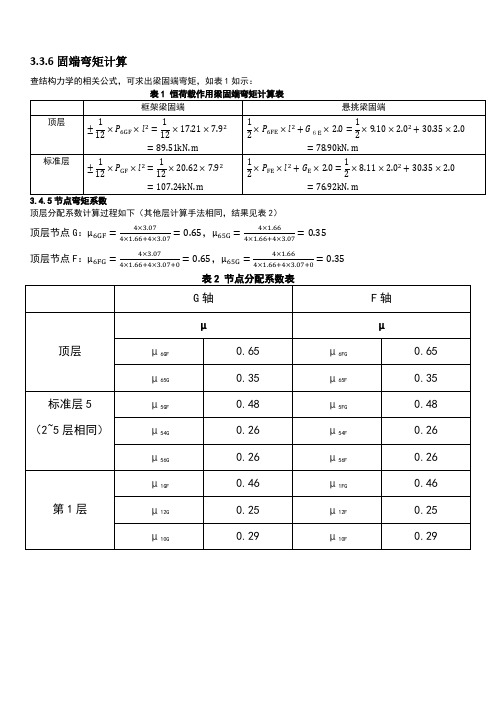
3.3.6固端弯矩计算查结构力学的相关公式，可求出梁固端弯矩，如表1如示：3.4.5节点弯矩系数顶层分配系数计算过程如下（其他层计算手法相同，结果见表2）顶层节点G：μ6GF=4×3.074×1.66+4×3.07=0.65，μ65G=4×1.664×1.66+4×3.07=0.35顶层节点F：μ6FG=4×3.074×1.66+4×3.07+0=0.65，μ65G=4×1.664×1.66+4×3.07+0=0.353.6.6恒荷载作用下内力分析【1】力矩二次分配恒荷载作用下内力计算采用力矩二次分配法，计算结果程见下图：（注：3~4层相同）【2】各层剪力V值按简支计算梁端剪力如下：顶层：G轴，V6GF=17.27×7.9÷2=68.22kN，F轴，V6FG=−V6GF=−68.22kN，V6FE=9.10×2.0÷2+30.35=48.55kN 其他层：G轴，V GF=20.62×7.9÷2=81.45kN，F轴，V FG=−V GF=−81.45kN，V6FE=8.11×2.0÷2+30.35=38.46kN 二次分配后，梁、柱端剪力计算如下：(以顶层为例)梁：V6GF=68.22−95.36−41.607.9=61.41kN，V6FG=−68.22−95.36−41.607.9=−75.03kNV6FE=48.55kN柱：G柱，V=−（−16.16−14.92）3.5=8.97kN，F柱V=−（41.60+37.74）3.5=−22.67kN剪力图见（恒载作用下剪力图）【3】各层柱轴力N值：轴力图见（恒载作用下轴力图）【4】内力调整及调整后弯矩图内力调整结果见下表：M边=M−V×b2；V边=V−q×b2，b为柱宽M中=M0−(V边G+V边F÷2)，M0为按简支计算的原跨中弯矩；顶层M0=134.26，其他层M0=160.86恒荷载内力调整（β取0.8）层次截面柱轴线处柱边缘处跨中M V M边V边0.8M M中天面G右41.60 61.41 29.31 57.97 23.4569.15 F左95.36 75.69 80.22 72.24 64.175G右73.76 77.01 50.66 73.57 40.5382.64 F左108.85 86.32 91.59 82.88 73.273~4G右72.93 76.78 49.90 73.33 39.9282.63 F左109.85 86.58 92.54 83.14 74.032G右72.68 76.75 49.65 73.31 39.7282.63 F左109.78 86.60 92.46 83.16 73.971G右68.09 76.34 52.82 72.90 42.2682.61 F左108.43 87.05 91.02 83.61 72.81。
