弯矩二次分配法 PPT课件

弯矩二次分配法(六层)弯矩二次分配法是一种常用的结构计算方法之一，可以有效地计算出结构中各部分的弯矩值和相应的受力情况。

这种方法具有计算简单、精度高、直观易懂等特点，被广泛应用于各类建筑结构的设计和分析中。

在本文中，我们将介绍弯矩二次分配法的基本原理、计算步骤和实例应用。

一、基本原理弯矩二次分配法的基本原理是通过叠加各种荷载的分布形态，逐步计算出结构中各个部分的受力情况。

具体来说，我们通过将荷载分解为若干小块，逐步计算每一块对结构的影响，并将计算结果叠加起来，最终得到整体的受力情况。

这种方法具有高精度、计算简单、可扩展性强等优点，通常被用于分析各种较为复杂的结构。

二、计算步骤弯矩二次分配法的计算步骤一般可以分为以下六层：1、确定结构模型和荷载模型首先，我们需要确定结构模型和荷载模型。

在确定结构模型时，应考虑结构的几何形状、材料特性、外部荷载等因素；在确定荷载模型时，应考虑荷载的大小、作用点、分布形态等因素。

这些因素的准确度决定了弯矩二次分配法的精度和可靠性。

2、绘制荷载图在确定好荷载模型后，我们需要将荷载分布情况用荷载图的形式表示出来。

荷载图一般采用坐标轴表示，将X轴和Y轴分别表示荷载和受力的距离，通过指定不同的坐标值来表示荷载的大小和作用点。

3、计算受力分布坐标接下来，我们需要根据荷载图和结构模型来计算出受力分布坐标，即测量出各个部位的受力位置和受力大小。

这一步骤需要注意测量的精度和准确性，以确保后续的计算能够得到准确的结果。

在测量出受力分布坐标后，我们需要根据受力分布的情况来计算初次的受力分布情况。

这个过程中，我们需要考虑各个部位的受力情况和相互之间的作用，以确定初次的受力分布。

在计算出初次的受力分布后，我们需要根据改变系经验公式来进行弯矩二次分配计算，用窗口法和直接交错法得到二次受力分布，这一步骤非常重要，因为它可以精确地计算出各个部分的弯矩值，从而为后续的结构分析提供参考。

6、计算最终反力分布通过计算得到二次受力分布后，我们就可以根据材料特性和式子进行最终的反力分布计算。

弯矩二次分配法弯矩二次分配法是一种钢结构设计中常用的计算方法，其基本思想是根据节点处的位移来分配节点上的弯矩，以达到平衡整个结构的弯矩。

下面对弯矩二次分配法进行详细介绍。

一、基本概念1、刚度法刚度法是一种以刚度为基础的计算方法。

在此方法中，我们将受力结构看作由若干个刚度性能已知的元件构成的刚性系统，根据受力原理对每个元件计算弯矩以及位移，最终得到完整结构的弯矩和位移。

2、节点法弯矩二次分配法是一种常用的节点法计算方法，其基本原理如下：1、首先将结构分成若干截，根据节点的位移和角位移分别计算每截内部的弯矩；2、根据弯矩平衡条件，推断出每个截面的弯矩；3、通过利用每个截面上的弯矩平衡条件，把原来被认为是剪力作用的分量分离出来，并计算出其大小；4、根据剪力大小，重新计算每截的弯矩，并迭代计算至弯矩平衡条件满足为止。

1、假设结构内部没有产生任何形变，即所有截面处的弯矩相等；2、对于一个结构，它的初始刚度矩阵和转动角度矩阵分别为：K = [M] / δθ = [K]·[P]其中，[M]是结构的初始均布荷载矩阵，δ是结构的初始弯矩；[P]是节点位移矩阵，[K]是结构的初始刚度矩阵。

3、经过第一次迭代后，结构的弯矩为:M' = K'·δ'其中，δ'是第一次迭代后的位移矩阵，K'是经过调整后的刚度矩阵。

6、根据每个截面上的剪力和弯矩重新计算每截的弯矩；7、重复步骤4~6，直至迭代计算出的弯矩满足平衡条件；8、得到最终的弯矩分布图。

优点：1、计算结果精确，特别适用于刚梁、钢架等结构的计算；2、计算实现简单，易于应用于各种计算软件中；3、计算时间相对较短，计算效率高。

1、操作复杂，需要依次进行多个迭代计算；2、计算过程中需要多次使用刚度矩阵，可能会造成精度误差；3、计算结果不太适用于拉杆、压杆等主要受轴向载荷的结构计算。

（2）分配系数：
经过观察，发现第⑨轴横向框架为对称结构，且受对称荷载的作用，所以可以取一半结构计算；要注意到，接头处简化为滑动支座，由此带来跨中梁线刚度增大一倍，且分配系数有所不同。

分配系数计算公式：1
i i n i i S S
μ==∑ （3.26）
其中：i S 为转动刚度，两端固支杆4i S i =，一端固支，一端滑动固支杆i S i = n 为该节点所连接的杆件数。

由此计算出各个杆件分配系数，标绘于计算简图上。

然后利用力矩二次分配法计算第⑨轴框架杆端弯矩。

如图3.19。

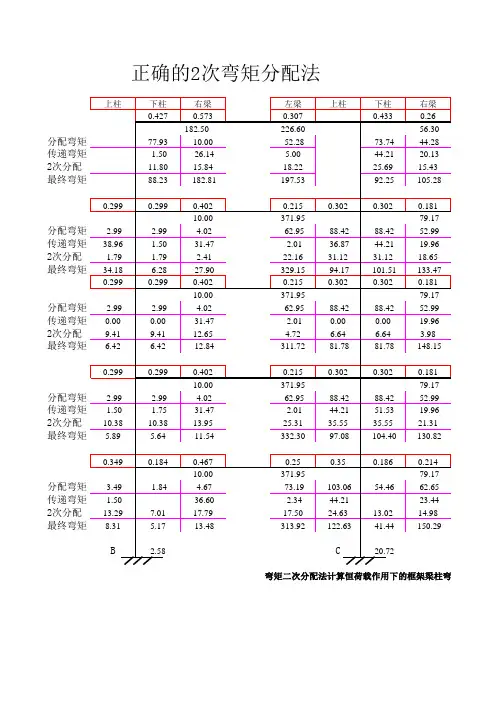
注：图中单线条表示第一次分配结束，双线条表示第二次分配结束，虚线表示固端弯矩，粗实线表示最终杆端弯矩。

节点外弯矩以顺时针为正，逆时针为负，标绘于计算简图上。

图3.19 恒载弯矩二次分配计算简图。

二次矩形分配法
二次矩形分配法是指弯矩二次分配法，是一种用来计算力的方法。

竖向荷载作用下内力近似计算，具体计算步骤：
（1）根据各杆件的转动刚度计算各节点的杆端弯矩分配系数，并计算竖向荷载作用下各跨梁的固端弯矩。

（2）计算框架各节点的不平衡弯矩，并对所有节点的不平衡弯矩同时进行第一次分配（其间不进行弯矩传递）。

（3）将所有杆端的分配弯矩同时向其远端传递（对于刚接框架，传递系数均取1/2）。

（4）将各节点因传递弯矩而产生的新的不平衡弯矩进行第二次分配，使各节点处于平衡状态。

至此，整个弯矩分配和传递过程即告结束。

（5）将各杆端的固端弯矩、分配弯矩和传递弯矩叠加，即得各杆端弯矩。

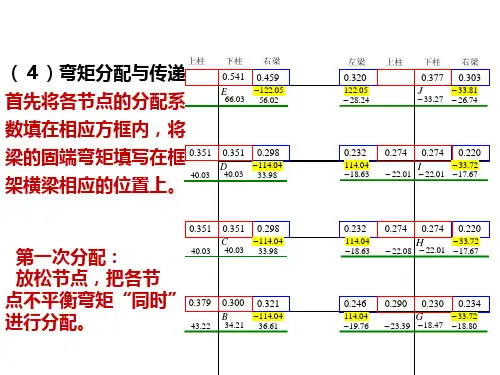
弯矩二次分配法求杆端弯矩好了，今天咱们聊聊弯矩二次分配法，听起来是不是有点深奥？其实嘛，说白了，这个方法就像是给你一根杆子，然后看它弯成什么样，最后帮你找到杆子各个地方的弯矩。

你说，弯矩听起来不就是一个让东西弯曲的力量吗？没错，就是这么回事。

今天，咱们就把这件看起来复杂的事情，给它拆解开来，一步步讲清楚。

你知道，在工程结构设计中，遇到梁、杆这些东西，弯矩就成了大头。

杆子上哪儿弯了，受了多大的力，这些都是必须得搞清楚的。

所以，弯矩二次分配法就是帮助我们计算这些弯矩的一个小工具。

它不需要咱们做那些复杂的手工计算，反而是通过一种巧妙的分配方式，把这些弯矩从一个地方“传递”到另一个地方。

说起来简单，但要弄明白，确实得下点功夫。

得理解个概念。

咱们常常会在杆子上装几个支座，对吧？这些支座能让杆子稳稳地撑住，防止它掉下来。

但在这些支座之间，杆子可不总是直的。

它会因为外力的作用，变得弯曲。

某个地方受力特别大，弯矩也特别大，结果就可能出现结构不稳定的问题。

所以，我们得精确算出每个支座之间，杆子每个位置的弯矩，才能保证设计不出错。

说到这里，咱们就得用到弯矩二次分配法了。

这方法特别巧妙，像是一个弯弯绕绕的小道理。

简单地说，弯矩二次分配法就是一种“按比例分配”的方法。

什么意思呢？就像你分蛋糕，大家按自己的份额来拿，谁多，谁少。

这个“蛋糕”就是杆子的弯矩，分配的规则就是通过杆子两端支座之间的相互关系来决定。

别小看这个“分配”，它可比蛋糕分配复杂得多。

咱们要先搞清楚杆子上各个支座的反力，然后再来分配弯矩。

就拿一个简单的支撑梁来说，两个支座承受的反力不同，这时候就要根据反力的大小，来决定弯矩在杆子上的分布。

大致上，弯矩会根据这个比例“二次分配”到各个支座和节点上。

就好像你请了一帮朋友来分担家务，有的人擦窗户，有的人扫地，分工明确，每个人都根据自己的情况去做，最后的结果大家都不吃亏。

在这个过程中，你还得小心，不能乱分。

弯矩二次分配法的关键在于要准确计算出每个点的弯矩，并且这些计算得通过迭代的方式一步一步进行。

弯矩二次分配法弯矩二次分配法是一种用于处理多成分系统优化问题的方法。

它结合了反比例定律、动态规划和解析几何学等多学科技术，可以有效地解决多成分系统优化问题。

它为解决复杂的在线优化问题提供了新的解决思路。

弯矩二次分配法的基本思想是将优化的多成分系统组合成弯矩函数，然后借助反比例定律和动态规划，将多变量的优化问题转换为弯矩函数的极值问题。

弯矩函数在极值问题中，可以采用解析几何学方法来求得极值点，从而获得问题的最优解。

它还可以使用改进的动态规划方法，将极值问题转换为搜索问题，从而有效解决高维的优化问题。

弯矩二次分配法的应用很广泛，包括工业优化、金融优化、机器学习优化等方面。

它主要用于多成分系统的优化，比如交通系统的优化、资源配置的优化等等。

针对上述问题，弯矩二次分配法可以采用反比例定律，将多变量问题转换为相关弯矩函数的极值问题，然后借助动态规划和解析几何学等技术来求解，从而获得问题的最优解。

弯矩二次分配法的另一个重要应用是定价的优化。

在定价优化中，有很多变量，如定价、促销时间、折扣等，它们之间是复杂的相互关系，由于其多变量性，单纯地采用传统的动态规划方法很难得到高效的最优解，而采用弯矩二次分配法可以有效解决这个问题。

此外，弯矩二次分配法在多终端视频压缩技术中也有广泛的应用。

多终端视频压缩技术涉及多终端网络和视频通道，多个终端网络之间的压缩参数有复杂的相互关系，由于其多变量性，单纯地采用传统的动态规划方法无法得到高效的最优解，而采用弯矩二次分配法可以有效地解决这个问题。

总的来说，弯矩二次分配法是一种实用的多成分系统优化方法，它结合了反比例定律、动态规划和解析几何学等多学科技术，在多成分系统优化问题中取得了很大的进展，并可以有效解决复杂的在线优化问题。

由于其多功能性，它也被广泛应用于工业优化、金融优化和机器学习优化等多个领域，为解决复杂优化问题提供了有用的解决方案。