恒载弯矩二次分配法计算表格.xls
- 格式:xls
- 大小:33.50 KB
- 文档页数:3

弯矩二次分配法excel弯矩二次分配法(Moment Distribution Method)是结构分析中常用的一种计算方法,适用于解决梁、桁架等结构的弯矩分配问题。
通过多次迭代计算,可以准确地求解结构的内力分布。
在Excel中,可以使用各种函数和公式来实现弯矩二次分配法的计算。
首先,需要建立一个适当的数据表格,包括输入数据和计算结果。
输入数据通常包括结构的几何尺寸、材料性质、荷载大小和位置等。
计算结果包括节点的位移、弯矩和剪力等。
为了进行弯矩二次分配法的计算,首先需要确定结构的支座刚度矩阵。
支座刚度矩阵包括结构的刚度和弯矩分配系数。
可以使用Excel中的数组函数来计算支座刚度矩阵。
然后,根据结构的约束条件,可以得到初始的节点位移。
接下来,需要进行迭代计算,直至收敛。
在每一次迭代中,需要计算每个节点的弯矩分配系数和弯矩修正系数。
可以使用Excel中的循环函数和条件函数来实现这一步骤。
然后,根据弯矩分配系数和弯矩修正系数,可以计算每个节点的弯矩和剪力。
在完成迭代计算后,可以得到结构的最终结果,包括节点的位移、弯矩和剪力。
可以使用Excel中的图表功能来可视化结果,并进行必要的分析和评估。
需要注意的是,弯矩二次分配法是一种近似方法,结果的精度受到迭代次数和初始条件的影响。
因此,在使用Excel进行计算时,需要进行适当的设置和调整,以保证结果的准确性和可靠性。
总之,通过在Excel中使用弯矩二次分配法,可以方便地进行结构的弯矩分析。
这种方法的优点是简单易用,适用于各种结构类型。
然而,对于复杂的结构和边界条件,可能需要借助更为专业的结构分析软件来进行分析和计算。
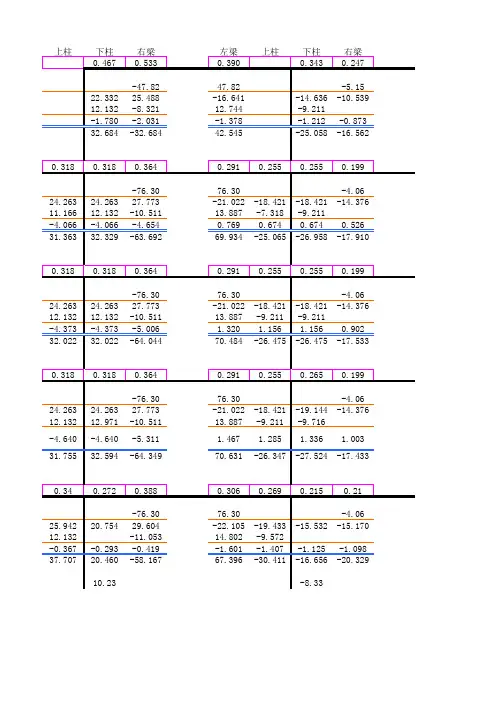
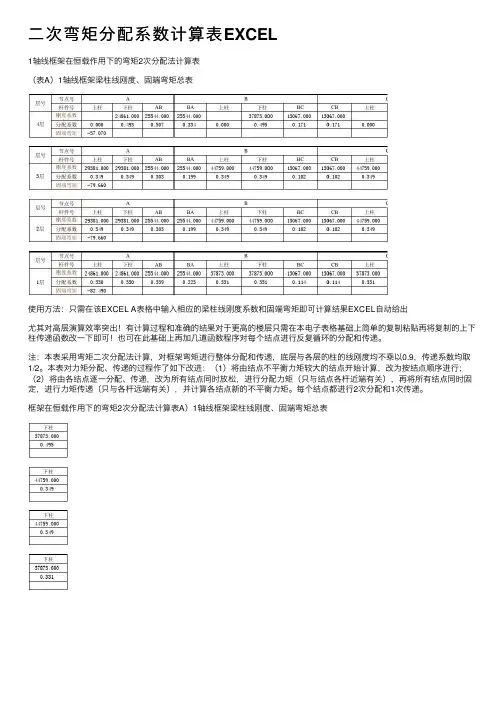
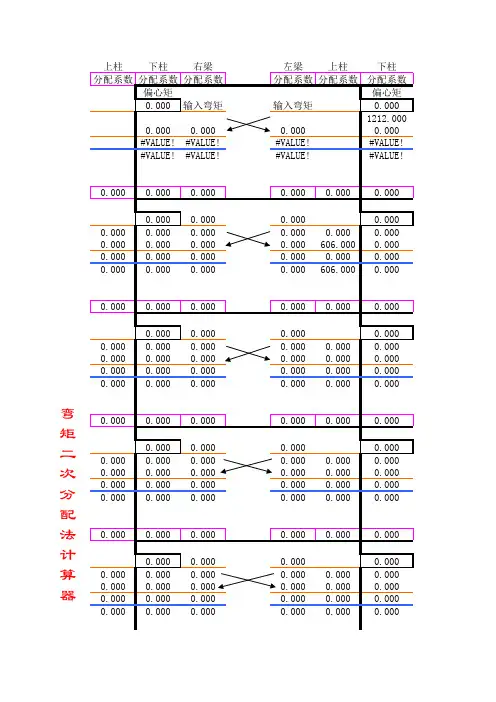
⼆次弯矩分配系数计算表EXCEL
1轴线框架在恒载作⽤下的弯矩2次分配法计算表
(表A)1轴线框架梁柱线刚度、固端弯矩总表
使⽤⽅法:只需在该EXCEL A表格中输⼊相应的梁柱线刚度系数和固端弯矩即可计算结果EXCEL⾃动给出
尤其对⾼层演算效率突出!有计算过程和准确的结果对于更⾼的楼层只需在本电⼦表格基础上简单的复制粘贴再将复制的上下柱传递函数改⼀下即可!也可在此基础上再加⼏道函数程序对每个结点进⾏反复循环的分配和传递。
注:本表采⽤弯矩⼆次分配法计算,对框架弯矩进⾏整体分配和传递,底层与各层的柱的线刚度均不乘以0.9,传递系数均取1/2。
本表对⼒矩分配、传递的过程作了如下改进:(1)将由结点不平衡⼒矩较⼤的结点开始计算,改为按结点顺序进⾏;(2)将由各结点逐⼀分配、传递,改为所有结点同时放松,进⾏分配⼒矩(只与结点各杆近端有关),再将所有结点同时固定,进⾏⼒矩传递(只与各杆远端有关),并计算各结点新的不平衡⼒矩。
每个结点都进⾏2次分配和1次传递。
框架在恒载作⽤下的弯矩2次分配法计算表A)1轴线框架梁柱线刚度、固端弯矩总表
C
C
C
C
(表B )弯矩2次分配与传递表4层。

弯矩二次分配法excel弯矩二次分配法(Moment Distribution Method)是一种用于计算连续梁和框架结构内力的方法。
它的原理是通过数值迭代的方式来逐步分配弯矩,直到收敛为止。
这种方法在工程实践中广泛应用,其计算结果精确可靠。
弯矩二次分配法的基本步骤如下:1. 绘制结构的荷载图和剪力图首先,根据结构的几何形状和荷载情况,绘制出整个结构的荷载图和剪力图。
这些图用于确定结构中各个节点的边界条件和外力作用点。
2. 划分初始刚度矩阵将结构按照其自由度进行划分,建立初始的刚度矩阵。
每个节点的自由度包括水平位移和转角,而每个单元的自由度包括剪力和弯矩。
刚度矩阵记录了结构中各个单元之间的刚度关系。
3. 进行弯矩分配根据结构的初始刚度矩阵以及节点的边界条件,通过弯矩分配的方法来逐步计算每个单元的剪力和弯矩。
首先,将全局外力施加到结构上,然后根据初始刚度矩阵和外力计算出每个单元的初始剪力和弯矩。
接下来,按照一定的迭代顺序,将每个单元的剪力和弯矩按照一定的比例分配给相邻的单元,然后更新刚度矩阵。
直到满足一定的收敛条件,即剪力和弯矩的分配趋于稳定,这个过程称为弯矩分配。
4. 计算节点位移在进行了弯矩分配之后,根据节点边界条件和每个单元的位移,可以计算出每个节点的位移。
这里使用弯矩二次分配法的一个重要假设,即梁在弯曲作用下可以看作刚性倍增杆,因此弯曲刚度与柔度成反比。
5. 更新刚度矩阵根据已知的节点位移和单元位移,可以更新刚度矩阵。
通过多次迭代计算,直到满足一定的收敛条件。
6. 计算内力最后,在完成弯矩分配和节点位移计算之后,根据梁的基本原理和弯矩分配法的结果,可以得到结构中各个节点和单元的内力。
以上是弯矩二次分配法的基本步骤,通过这种方法可以计算得到结构中各个节点和单元的内力分布。
这种方法在实际工程中广泛应用,尤其是对于复杂结构的计算分析非常有用。
在Excel中,可以通过建立相应的计算模型和公式来实现弯矩二次分配法的计算。

弯矩二次分配法excel弯矩二次分配法是一种常见的结构力学分析方法,通过计算结构不同部位的弯矩,将其进行二次分配,并对不同部位进行设计,从而保证结构的稳定性、安全性和经济性。
在实际工程项目中,弯矩二次分配法被广泛应用于房屋、桥梁、塔架等各种建筑和工程结构的设计与分析。
在使用弯矩二次分配法进行结构分析时,通常需要进行如下步骤:1. 分析结构荷载:首先需要根据实际情况进行结构荷载的分析,包括自重、活载、风荷载、地震荷载等。
2. 计算结构弯矩:根据结构荷载,通过静力学或弹性力学的方法计算出不同位置处的结构弯矩。
3. 进行一次分配:由于结构不同部位承受的荷载和弯矩不同,需要将总弯矩进行一次分配,确定各部位的弯矩大小。
4. 进行二次分配:在确定了各部位的弯矩大小后,需要进行二次分配,将每个部位的弯矩进一步分配到局部构件或构件组上,以便进行设计和计算。
5. 进行设计:在得出各构件或构件组的弯矩大小后,需要进行设计选型,并进行受力分析,以满足结构稳定性和安全性的要求。
在Excel中,可以通过以下步骤进行弯矩二次分配法的计算:1. 输入荷载:选择合适的单元格,输入结构的自重、活载、风荷载、地震荷载等荷载数据。
2. 计算弯矩:通过Excel中的公式,根据荷载及结构条件,计算出不同位置处的结构弯矩,输入到相应的单元格内。
3. 一次分配:通过Excel中的公式,将总弯矩进行一次分配,确定各部位的弯矩大小,并输入到相应的单元格内。
4. 二次分配:根据设计要求和结构特点,将每个部位的弯矩进一步分配到局部构件或构件组上,并输入到相应的单元格内。
5. 设计:根据具体情况和设计规范,选择合适的结构构件,并进行受力分析,以满足结构稳定性和安全性的要求。
需要注意的是,在进行Excel分析时,需要准确输入数据并使用正确的公式,同时也需要严格按照结构设计规范和要求进行计算和设计,以保证分析结果的准确性和可靠性。
总之,弯矩二次分配法是一种重要的结构力学分析方法,在实际工程项目中具有广泛的应用和重要的意义。
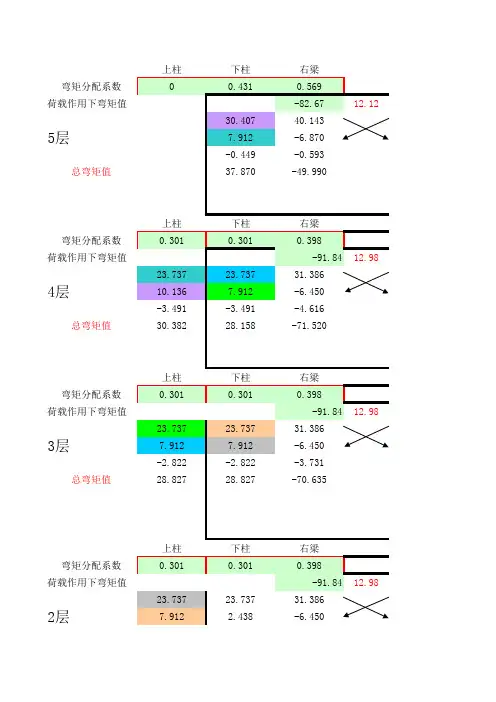
上柱下柱右梁弯矩分配系数00.4310.569荷载作用下弯矩值-82.6712.1230.40740.1435层7.912-6.870-0.449-0.593总弯矩值37.870-49.990上柱下柱右梁弯矩分配系数0.3010.3010.398荷载作用下弯矩值-91.8412.9823.73723.73731.3864层10.1367.912-6.450-3.491-3.491-4.616总弯矩值30.38228.158-71.520上柱下柱右梁弯矩分配系数0.3010.3010.398荷载作用下弯矩值-91.8412.9823.73723.73731.3863层7.9127.912-6.450-2.822-2.822-3.731总弯矩值28.82728.827-70.635上柱下柱右梁弯矩分配系数0.3010.3010.398荷载作用下弯矩值-91.8412.9823.73723.73731.3862层7.912 2.438-6.450-1.174-1.174-1.552总弯矩值30.47525.001-68.456上柱下柱右梁弯矩分配系数0.2540.40.346荷载作用下弯矩值-91.8463.047.31511.5209.9651层7.912-5.368-0.646-1.018-0.880总弯矩值14.58110.502-88.124柱底弯矩值 5.251左梁上柱下柱右梁左梁0.21500.1630.6220.792 82.670-7.72-11.047.72-13.741-10.417-39.752-0.713 20.071-3.254-0.356-19.876-3.539-2.683-10.23915.828 85.462-16.355-58.067 2.959左梁上柱下柱右梁左梁0.1850.140.140.5350.65691.84-6.63-15.48 6.63 -12.900-9.762-9.762-37.306-1.246 15.693-3.472-3.254-0.623-18.653-1.544-1.168-1.168-4.46412.349 93.090-14.403-14.184-49.022-0.921左梁上柱下柱右梁左梁0.1850.140.140.5350.65691.84-6.63-15.48 6.63 -12.900-9.762-9.762-37.306-1.246 15.693-3.254-3.254-0.623-18.653-1.584-1.199-1.199-4.58112.379 93.049-14.215-14.215-49.139-0.890左梁上柱下柱右梁左梁0.1850.140.140.5350.65691.84-6.63-15.48 6.63 -12.900-9.762-9.762-37.306-1.246 15.693-3.254-2.627-0.623-18.653-1.700-1.286-1.286-4.91611.856 92.933-14.303-13.676-49.475-1.413左梁上柱下柱右梁左梁0.1730.1270.20.50.60491.84-6.63-23.15 6.63 -10.736-7.882-12.412-31.0308.1044.982-3.254 4.052-15.515-1.000-0.734-1.156-2.8909.437 85.086-11.870-13.568-36.4988.656-6.784上柱下柱-6.82上柱下柱0.1720.172-4.73 -0.327-0.327-0.062-0.1093.238 3.2382.849 2.802上柱下柱0.1720.172-4.73 -0.327-0.327-0.109-0.1093.246 3.2462.810 2.810上柱下柱-4.73 -0.327-0.327-0.1090.6893.109 3.1092.6733.471上柱下柱0.1540.242-20.048 2.066 3.247-0.1092.4063.7814.3647.0283.514。
