天津市南开中学高二数学必修5作业：一元二次不等式(2) Word版缺答案

课时训练16 一元二次不等式及其解法一、一元二次不等式的解法1.不等式-x 2-5x+6≤0的解集为( ) A.{x|x ≥6或x ≤-1} B.{x|-1≤x ≤6} C.{x|-6≤x ≤1} D.{x|x ≤-6或x ≥1} 答案:D解析:由-x 2-5x+6≤0得x 2+5x-6≥0,即(x+6)(x-1)≥0,∴x ≥1或x ≤-6.2.(2015福建厦门高二期末,12)不等式2x 2-5x+5>12的解集是 .答案:{x|x<2或x>3}解析:因为指数函数y=2x 是增函数,所以2x2-5x+5>12化为x 2-5x+5>-1,即x 2-5x+6>0,解得x<2或x>3. 所以不等式的解集为{x|x<2或x>3}. 3.解不等式:-2<x 2-3x ≤10.解:原不等式等价于不等式组{x 2-3x >-2,x 2-3x ≤10,①②不等式①为x 2-3x+2>0,解得x>2或x<1. 不等式②为x 2-3x-10≤0,解得-2≤x ≤5. 故原不等式的解集为[-2,1)∪(2,5].二、三个二次之间的关系4.(2015山东威海高二期中,8)不等式ax 2+bx+2>0的解集是{x |-12<x <13},则a-b 的值为( )A.14B.-14C.10D.-10答案:D解析:不等式ax 2+bx+2>0的解集是{x |-12<x <13},可得-12,13是一元二次方程ax 2+bx+2=0的两个实数根,∴-12+13=-b a ,-12×13=2a ,解得a=-12,b=-2.∴a-b=-12-(-2)=-10.故选D .5.如果ax 2+bx+c>0的解集为{x|x<-2或x>4},那么对于函数f (x )=ax 2+bx+c ,f (-1),f (2),f (5)的大小关系是 . 答案:f (2)<f (-1)<f (5)解析:由ax 2+bx+c>0的解集为{x|x<-2或x>4}知a>0,且-2,4是方程ax 2+bx+c=0的两实根,所以{-2+4=-ba ,-2×4=c a ,可得{b =-2a ,c =-8a ,所以f (x )=ax 2-2ax-8a=a (x+2)(x-4). 因为a>0,所以f (x )的图象开口向上.又对称轴方程为x=1,f (x )的大致图象如图所示,由图可得f (2)<f (-1)<f (5).6.(2015山东潍坊四县联考,11)不等式x 2-ax-b<0的解集是(2,3),则不等式bx 2-ax-1>0的解集是 . 答案:(-12,-13)解析:∵不等式x 2-ax-b<0的解集为(2,3),∴一元二次方程x 2-ax-b=0的根为x 1=2,x 2=3.根据根与系数的关系可得:{2+3=a ,2×3=-b ,所以a=5,b=-6.不等式bx 2-ax-1>0,即不等式-6x 2-5x-1>0, 整理,得6x 2+5x+1<0,即(2x+1)(3x+1)<0,解之得-12<x<-13.∴不等式bx 2-ax-1>0的解集是(-12,-13). 三、含参不等式的解法7.不等式(x+1)(x-a )<0的解集为{x|-1<x<2},则不等式ax+1x -1>1的解集为 .答案:{x|x<-2或x>1}解析:由已知不等式(x+1)(x-a )<0的解集为{x|-1<x<2}得x=2是(x+1)(x-a )=0的一个根,∴a=2. ∴不等式ax+1x -1>1可化为2x+1x -1>1,移项通分得x+2x -1>0, ∴(x+2)(x-1)>0,解得x<-2或x>1. ∴所求解集为{x|x<-2或x>1}.8.解关于x 的不等式2x 2+ax+2>0.解:对于方程2x 2+ax+2=0,其判别式Δ=a 2-16=(a+4)(a-4).①当a>4或a<-4时,Δ>0,方程2x 2+ax+2=0的两根为:x 1=14(-a-√a 2-16),x 2=14(-a+√a 2-16).∴原不等式的解集为{x |x <14(-a -√a 2-16)或x >14(-a +√a 2-16)}.②当a=4时,Δ=0,方程有两个相等实根,x 1=x 2=-1;当a=-4时,Δ=0,方程有两个相等实根,x 1=x 2=1.∴原不等式的解集为{x|x ≠±1}. 四、不等式恒成立问题9.若一元二次不等式x 2-ax+1>0恒成立,则a 的取值范围是 . 答案:-2<a<2解析:由Δ=a 2-4<0,解得-2<a<2.10.已知关于x 的不等式(m 2+4m-5)x 2-4(m-1)x+3>0对一切实数x 恒成立,求实数m 的取值范围. 解:(1)当m 2+4m-5=0,即m=1或m=-5时,显然m=1符合条件,m=-5不符合条件;(2)当m 2+4m-5≠0时,由二次函数对一切实数x 恒为正数, 得{m 2+4m -5>0,Δ=16(m -1)2-12(m 2+4m -5)<0, 解得1<m<19.综合(1)(2)得,实数m 的取值范围为[1,19).(建议用时:30分钟)1.不等式-6x 2-x+2≤0的解集是( ) A.{x |-23≤x ≤12}B.{x |x ≤-23,或x ≥12} C.{x |x ≥12}D.{x |x ≤-23} 答案:B解析:原不等式等价于6x 2+x-2≥0.方程6x 2+x-2=0的两根为-23,12,可得原不等式的解集为{x |x ≤-23,或x ≥12}.2.函数y=√x 2-2x -3+log 2(x+2)的定义域为 ( )A.(-∞,-1)∪(3,+∞)B.(-∞,-1]∪[3,+∞)C.(-2,-1]D.(-2,-1]∪[3,+∞) 答案:D解析:要使函数有意义,x 的取值需满足{x 2-2x -3≥0,x +2>0,解得-2<x ≤-1或x ≥3.3.已知0<a<1,关于x 的不等式(x-a )(x -1a )>0的解集为( ) A.{x |x <a 或x >1a } B.{x|x>a } C.{x |x <1a 或x >a} D.{x |x <1a } 答案:A解析:∵0<a<1,∴1a >1,即a<1a ,∴不等式的解集为{x |x >1a 或x <a}.4.在R 上定义运算|a cb d|=ad-bc ,若|x 3-x x |<|2 01 2|成立,则x 的取值范围是( )A.{x|x<-4或x>1}B.{x|-4<x<1}C.{x|x<-1或x>4}D.{x|-1<x<4}答案:B 解析:由已知|x 3-x x|=x 2+3x ,|2 01 2|=4, ∴x 2+3x<4,即x 2+3x-4<0,解得-4<x<1.5.若关于x 的不等式ax-b>0的解集为(1,+∞),则关于x 的不等式ax+bx -2>0的解集为( )A.(-1,2)B.(-∞,-1)∪(2,+∞)C.(1,2)D.(-∞,-2)∪(1,+∞)答案:B解析:因为关于x 的不等式ax-b>0的解集为(1,+∞),所以a>0,且ba =1,即a=b ,所以关于x 的不等式ax+b x -2>0可化为x+1x -2>0,其解集是(-∞,-1)∪(2,+∞). 6.已知二次方程ax 2+bx+c=0的两个根是-2,3,若a>0,那么ax 2-bx+c>0的解集是 . 答案:{x|x<-3或x>2}解析:由题意知{-ba =-2+3,c =-2×3,∴b=-a ,c=-6a.∴不等式ax 2-bx+c>0,化为ax 2+ax-6a>0,又∵a>0,∴x 2+x-6>0,而方程x 2+x-6=0的根为-3和2,∴不等式的解集是{x|x<-3或x>2}.7.已知关于x 的不等式x 2-ax+2a>0在R 上恒成立,则实数a 的取值范围是 . 答案:(0,8)解析:由题意得,Δ=(-a )2-4×2a<0.即a 2-8a<0,∴0<a<8.8.设0≤α≤π,不等式8x 2-(8sin α)x+sin α≥0的解集为R ,则α的取值范围是 . 答案:[0,π6]∪[5π6,2π]解析:由已知不等式的解集为R ,∴Δ=64sin 2α-32sin α≤0,解得0≤sin α≤12. ∴由y=sin x 的图象知,当0≤α≤π时,解得0≤α≤π6或5π6≤α≤π.9.已知不等式x 2-2x-3<0的解集为A ,不等式x 2+4x-5<0的解集为B , (1)求A ∪B ;(2)若不等式x 2+ax+b<0的解集是A ∪B ,求ax 2+x+b<0的解集. 解:(1)解不等式x 2-2x-3<0,得A={x|-1<x<3}.解不等式x 2+4x-5<0,得B={x|-5<x<1}.∴A ∪B={x|-5<x<3}.(2)由x 2+ax+b<0的解集为{x|-5<x<3},∴{25-5a +b =0,9+3a +b =0,解得{a =2,b =-15.∴2x 2+x-15<0.∴不等式解集为{x |-3<x <52}.10.解关于x 的不等式:ax 2-2≥2x-ax (a<0). 解:原不等式移项得ax 2+(a-2)x-2≥0,化简为(x+1)(ax-2)≥0.∵a<0,∴(x+1)(x -2a )≤0.当-2<a<0时,2a≤x ≤-1; 当a=-2时,x=-1; 当a<-2时,-1≤x ≤2a . 综上所述,当-2<a<0时,解集为{x |2a ≤x ≤-1}; 当a=-2时,解集为{x|x=-1}; 当a<-2时,解集为{x |-1≤x ≤2a }.。

第三章不等式
一元二次不等式及其解法
第课时含参数的一元二次不等式的解法
级基础巩固
一、选择题
．不等式＜的解集为( )
．(－，)∪(，＋∞) ．(－∞.－)∪(，)
．(－，) ．(－∞，－)
解析：因为＜，所以＋＜，
即＜－.
答案：
．设＋＞，则关于的不等式(－)(＋)＞的解是( )
．＜－或＞．－＜＜
．＜－或＞．－＜＜
解析：方程(－)(＋)＝的两根为，－，
因为＋＞，所以＞－，结合函数＝(－)(＋)的图象，得原不等式的
解是－＜＜，故选.
答案：．已知不等式－－≥的解集是则不等式－－＜的解集是( )
．(，) ．(－∞，)∪(，＋∞)
∪
解析：由题意知－，－是方程－－＝的根，所以由根与系数的关
系得－＋＝，－×＝－.解得＝－，＝, 不等式－－＜即为－＋＜，解
集为(，)，
答案：
.二次函数()的图象如图所示，则(－)＞的解集为( )
．(－，)
．(，)
．(，]
．(－∞，)∪(，＋∞)
解析：由题图，知()＞的解集为(－，)．把()的图象向右平移个单
位长度即得(－)的图象，所以(－)＞解集为(，)．
答案：
．不等式≤的解集为( )
∪
∪
解析：原不等式等价于
即即－＜≤.
故原不等式的解集为
答案：
二、填空题
．不等式＋＋＞恒成立的条件是．
解析：由Δ＝－·＜，解得：＜＜.
答案：＜＜．若函数＝(为常数)的定义域为，则的取值范围是．
解析：函数＝的定义域为，即－＋(＋)≥对一切∈恒成立，当＝。

3.2 一元二次不等式及其解法（二）1.设集合M={a，a+1}，N={x∈R|x2≤4}，若M∪N=N，则实数a的取值范围为（）A．[﹣1，2] B．[﹣2，1] C．[﹣2，2] D．（﹣∞，﹣2]∪[2，+∞）2. 已知2a+1＜0，关于x的不等式x2﹣4ax﹣5a2＞0的解集是（）A．{x|x＞5a或x＜﹣a} B．{x|﹣a＜x＜5a} C．{x|x＜5a或x＞﹣a} D．{x|5a＜x＜﹣a}3.若max{s1，s2，…，s n}表示实数s1，s2，…，s n中的最大者．设A=（a1，a2，a3），，记A⊗B=max{a1b1，a2b2，a3b3}．设A=（x﹣1，x+1，1），，若A⊗B=x﹣1，则x的取值范围为（）A．B．C．D．4. 若不等式x2+2x﹣3≥0的解集是（）A．{x|﹣3≤x≤1}B．{x|x≤﹣3或x≥1}C．{x|x≥1}D．{x|x≤﹣3}5. 不等式的（x﹣2）（2x﹣3）＜0解集是（）A．（﹣∞，）∪（2，+∞）B．R C．（，2）D．φ6. 设关于x的不等式（ax﹣1）（x+1）＜0（a∈R）的解集为{x|﹣1＜x＜1}，则a的值是（）A．﹣2 B．﹣1 C．0 D．17. 设0＜b＜1+a，若关于x的不等式（x﹣b）2＞（ax）2的解集中的整数解恰有3个，则（）A．﹣1＜a＜0 B．0＜a＜1 C．1＜a＜3 D．3＜a＜68. 若关于x的不等式x2+ax﹣c＜0的解集为{x|﹣2＜x＜1}，对于任意的t∈[1，2]，函数f（x）=ax3+（m+）x2﹣c x在区间（t，3）上总不是单调函数，m的取什值范围是（）A．﹣＜m＜﹣3 B．﹣3＜m＜﹣1 C．﹣＜m＜﹣1 D．﹣3＜m＜09. 不等式2x2+mx+n＞0的解集是{x|x＞3或x＜﹣2}，则m，n的值分别是（）A．2，12 B．2，﹣2 C．2，﹣12 D．﹣2，﹣1210. 不等式﹣x2+3x+4＜0的解集为（）A．{x|﹣1＜x＜4} B．{x|x＞4或x＜﹣1} C．{x|x＞1或x＜﹣4} D．{x|﹣4＜x＜1}参考答案1.【解析】：由N={x∈R|x2≤4}={x∈R|﹣2≤x≤2}，又M∪N=N，则，解得：﹣2≤a≤1．∴实数a的取值范围为﹣2≤a≤1．故选：B．2. 【解析】不等式x2﹣4ax﹣5a2＞0可化为（x﹣5a）（x+a）＞0；∵方程（x﹣5a）（x+a）=0的两根为x1=5a，x2=﹣a，且2a+1＜0，∴a＜﹣，∴5a＜﹣a；∴原不等式的解集为{x|x＜5a，或x＞﹣a}．故选：C．3. 【解析】由A=（x﹣1，x+1，1），，得到A⊗B=max{x﹣1，（x+1）（x﹣2），|x﹣1|}=x﹣1，则，化简得，由①解得：1﹣≤x≤1+；由②解得x≥1，所以不等式组的解集为1≤x≤1+，则x的取值范围为[1，1+]故选B4.【解析】不等式x2+2x﹣3≥0可化为（x+3）（x﹣1）≥0，解得x≤﹣3，或x≥1；∴不等式的解集是{x|x≤﹣3或x≥1}．故选：B．5.【解析】∵不等式（x﹣2）（2x﹣3）＜0，解得＜x＜2；∴不等式的解集是（，2）故选：C．6.【解析】∵关于x的不等式（ax﹣1）（x+1）＜0（a∈R）的解集为{x|﹣1＜x＜1}，∴对应一元二次方程（ax﹣1）（x+1）=0的两个实数根为﹣1和1，∴x==1，或x=﹣1；∴a=1；即a的值是1．故选：D．7. 【解析】关于x的不等式（x﹣b）2＞（ax）2 即（a2﹣1）x2+2b x﹣b2＜0，∵0＜b＜1+a，[（a+1）x﹣b]•[（a﹣1）x+b]＜0 的解集中的整数恰有3个，∴a＞1，∴不等式的解集为＜x＜＜1，所以解集里的整数是﹣2，﹣1，0 三个．∴﹣3≤﹣＜﹣2，∴2＜≤3，2a﹣2＜b≤3a﹣3，∵b＜1+a，∴2a﹣2＜1+a，∴a＜3，综上，1＜a＜3，故选：C．8. 【解析】∵关于x的不等式x2+ax﹣c＜0的解集为{x|﹣2＜x＜1}，∴，解得a=1，c=2；∴f（x）=ax3+（m+）x2﹣c x=x3+（m+）x2﹣2x，求导得f′（x）=3x2+（2m+1）x﹣2；又∵对于任意的t∈[1，2]，f（x）在区间（t，3）上总不是单调函数，∴f′（x）在（2，3）上有零点，∴f′（2）f′（3）＜0，即[10+2（2m+1）][25+3（2m+1）]＜0，解得﹣＜m＜﹣3，∴m的取什值范围是﹣＜m＜﹣3．故选：A．9. 【解析】∵不等式2x2+mx+n＞0的解集是{x|x＞3或x＜﹣2}，∴一元二次方程2x2+mx+n=0的两个根为3，﹣2．由根与系数关系得：，解得：m=﹣2，n=﹣12．故选：D．10. 【解析】不等式﹣x2+3x+4＜0，因式分解得：（x﹣4）（x+1）＞0，可化为：或，解得：x＞4或x＜﹣1，则原不等式的解集为{x|x＞4或x＜﹣1}．故选B．。

(word完整版)高中数学必修5常考题型：一元二次不等式及其解法(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(word完整版)高中数学必修5常考题型：一元二次不等式及其解法(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(word完整版)高中数学必修5常考题型：一元二次不等式及其解法(word版可编辑修改)的全部内容。

一元二次不等式及其解法【知识梳理】1．一元二次不等式我们把只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式,即形如ax2＋bx＋c＞0(≥0)或ax2＋bx＋c＜0（≤0）（其中a≠0）的不等式叫做一元二次不等式．2．一元二次不等式的解与解集使一元二次不等式成立的x的值,叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集.3．一元二次不等式与相应的二次函数及一元二次方程的关系如表判别式Δ＝b2－4acΔ〉0Δ＝0Δ〈0一元二次方程ax2＋bx＋c＝0（a>0)的根有两相异实根x1,x2，(x1＜x2)有两相等实根x1＝x2＝－错误!没有实数根二次函数y＝ax2＋bx＋c（a〉0)的图象ax2＋bx＋c>0（a>0）的解集错误!或x>x2}错误!Rax2＋bx＋c 〈0(a>0)的解集{｝x|x1〈x〈x2∅∅题型一、一元二次不等式的解法【例1】解下列不等式：（1）2x2＋7x＋3＞0;（2）x2－4x－5≤0;（3）－4x2＋18x－错误!≥0；(4）－错误!x2＋3x－5＞0；（5)－2x2＋3x－2＜0。

高中数学必修5一元二次不等式及其解法精选题目（附答案）1．一元二次不等式我们把只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式，即形如ax2＋bx＋c＞0(≥0)或ax2＋bx＋c＜0(≤0)(其中a≠0)的不等式叫做一元二次不等式．2．一元二次不等式的解与解集使一元二次不等式成立的x的值，叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集．3．一元二次不等式与相应的二次函数及一元二次方程的关系表题型一：一元二次不等式解法1.解下列不等式：(1)2x2＋5x－3<0；(2)－3x2＋6x≤2；(3)4x2＋4x＋1>0；(4)－x2＋6x－10>0.题型二：三个“二次”关系的应用2.若不等式ax 2＋bx ＋2>0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <13，则a ＋b 的值为( )A ．14B ．－10C ．10D ．－143.已知一元二次不等式x 2＋px ＋q ＜0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12＜x ＜13，求不等式qx 2＋px ＋1＞0的解集．题型三：解含参数的一元二次不等式4.解关于x 的不等式x 2＋(1－a )x －a ＜0.巩固练习：1．不等式6x 2＋x －2≤0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－23≤x ≤12B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤－23或x ≥12 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥12D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤－23 2．设a <－1，则关于x 的不等式a (x －a )⎝ ⎛⎭⎪⎫x －1a <0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <a 或x >1a B ．{x |x >a } C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >a 或x <1aD.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <1a 3．在R 上定义运算⊙：a ⊙b ＝ab ＋2a ＋b ，则满足x ⊙(x －2)<0的实数x 的取值范围为( )A ．(0,2)B ．(－2,1)C ．(－∞，－2)∪(1，＋∞)D ．(－1,2)4．不等式mx 2－ax －1>0(m >0)的解集可能是( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－1或x >14 B ．R C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－13<x <32 D ．∅5．函数y ＝17－6x －x 2的定义域为( )A ．[－7,1]B ．(－7,1)C ．(－∞，－7]∪[1，＋∞)D ．(－∞，－7)∪(1，＋∞)6．已知全集U ＝R ，A ＝{x |x 2－1≥0}，则∁U A ＝________.7．若二次函数y ＝ax 2＋bx ＋c (a <0)的图象与x 轴的两个交点为(－1,0)和(3,0)，则不等式ax 2＋bx ＋c <0的解集是________．8．已知函数f (x )＝⎩⎨⎧x 2＋2x ，x ≥0，－x 2＋2x ，x <0.若f (a )≤3，则a 的取值范围是________．9．解关于x 的不等式x 2－3ax －18a 2>0. 10．若函数f (x )＝2 018ax 2＋2ax ＋2的定义域是R ，求实数a 的取值范围．参考答案：1.[解] (1)Δ＝49>0，方程2x 2＋5x －3＝0的两根为x 1＝－3，x 2＝12， 作出函数y ＝2x 2＋5x －3的图象，如图①所示．由图可得原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3<x <12.(2)原不等式等价于3x 2－6x ＋2≥0.Δ＝12>0，解方程3x 2－6x ＋2＝0，得x 1＝3－33，x 2＝3＋33，作出函数y ＝3x 2－6x ＋2的图象，如图②所示，由图可得原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤3－33或x ≥3＋33. (3)∵Δ＝0，∴方程4x 2＋4x ＋1＝0有两个相等的实根x 1＝x 2＝－12.作出函数y ＝4x 2＋4x ＋1的图象如图所示．由图可得原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠－12，x ∈R.(4)原不等式可化为x 2－6x ＋10<0，∵Δ＝－4<0， ∴方程x 2－6x ＋10＝0无实根，∴原不等式的解集为∅. 2.解：由已知得，ax 2＋bx ＋2＝0的解为－12，13，且a <0. ∴⎩⎪⎨⎪⎧－b a ＝－12＋13，2a ＝⎝ ⎛⎭⎪⎫－12×13，解得⎩⎨⎧a ＝－12，b ＝－2，∴a ＋b ＝－14.3.解：因为x 2＋px ＋q ＜0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12＜x ＜13，所以x 1＝－12与x 2＝13是方程x 2＋px ＋q ＝0的两个实数根，由根与系数的关系得⎩⎪⎨⎪⎧13－12＝－p ，13×⎝ ⎛⎭⎪⎫－12＝q ，解得⎩⎪⎨⎪⎧p ＝16，q ＝－16 .所以不等式qx 2＋px ＋1＞0即为－16x 2＋16x ＋1＞0，整理得x 2－x －6＜0，解得－2＜x ＜3.即不等式qx 2＋px ＋1＞0的解集为{x |－2＜x ＜3}．4.[解] 方程x 2＋(1－a )x －a ＝0的解为x 1＝－1，x 2＝a ，函数y ＝x 2＋(1－a )x －a 的图象开口向上，则当a ＜－1时，原不等式解集为{x |a ＜x ＜－1}；当a ＝－1时，原不等式解集为∅；当a ＞－1时，原不等式解集为{x |－1＜x ＜a }． 5.设a ∈R ，解关于x 的不等式ax 2＋(1－2a )x －2>0.5.解：(1)当a ＝0时， 不等式可化为x －2>0，解得x >2，即原不等式的解集为{x |x >2}．(2)当a ≠0时，方程ax 2＋(1－2a )x －2＝0的两根分别为2和－1a .①当a <－12时，解不等式得－1a <x <2，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1a <x <2；②当a ＝－12时，不等式无解，即原不等式的解集为∅；③当－12<a <0时，解不等式得2<x <－1a ，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2<x <－1a ； ④当a >0时，解不等式得x <－1a 或x >2，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－1a 或x >2. 练习：1.解析：选A 因为6x 2＋x －2≤0⇔(2x －1)·(3x ＋2)≤0，所以原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－23≤x ≤12. 2.解析：选A ∵a <－1，∴a (x －a )·⎝ ⎛⎭⎪⎫x －1a <0⇔(x －a )·⎝ ⎛⎭⎪⎫x －1a >0.又a <－1，∴1a >a ，∴x >1a 或x <a .3.解析：选B 由a ⊙b ＝ab ＋2a ＋b ，得x ⊙(x －2)＝x (x －2)＋2x ＋x －2＝x 2＋x －2<0，所以－2<x <1.4.解析：选A 因为Δ＝a 2＋4m >0，所以函数y ＝mx 2－ax －1的图象与x 轴有两个交点，又m >0，所以原不等式的解集不可能是B 、C 、D ，故选A.5.解析：选B 由7－6x －x 2>0，得x 2＋6x －7<0，即(x ＋7)(x －1)<0，所以－7<x <1，故选B.6.解析：∁U A ＝{x |x 2－1<0}＝{x |－1<x <1}． 答案：{x |－1<x <1}7.解析：根据二次函数的图象知所求不等式的解集为(－∞，－1)∪(3，＋∞)． 答案：(－∞，－1)∪(3，＋∞)8.解析：当a ≥0时，a 2＋2a ≤3，∴0≤a ≤1；当a <0时，－a 2＋2a ≤3，∴a <0.综上所述，a 的取值范围是(－∞，1]．9.解：将x 2－3ax －18a 2>0变形得(x －6a )(x ＋3a )>0， 方程(x －6a )(x ＋3a )＝0的两根为6a ，－3a .所以当a >0时，6a >－3a ，原不等式的解集为{x |x <－3a 或x >6a }；当a ＝0时，6a ＝－3a ＝0，原不等式的解集为{x |x ≠0}； 当a <0时，6a <－3a ，原不等式的解集为{x |x <6a 或x >－3a }． 10.解：因为f (x )的定义域为R ，所以不等式ax 2＋2ax ＋2>0恒成立． (1)当a ＝0时，不等式为2>0，显然恒成立；(2)当a ≠0时，有⎩⎨⎧ a >0，Δ＝4a 2－8a <0，即⎩⎨⎧a >0，0<a <2，所以0<a <2.综上可知，实数a 的取值范围是[0,2)．。

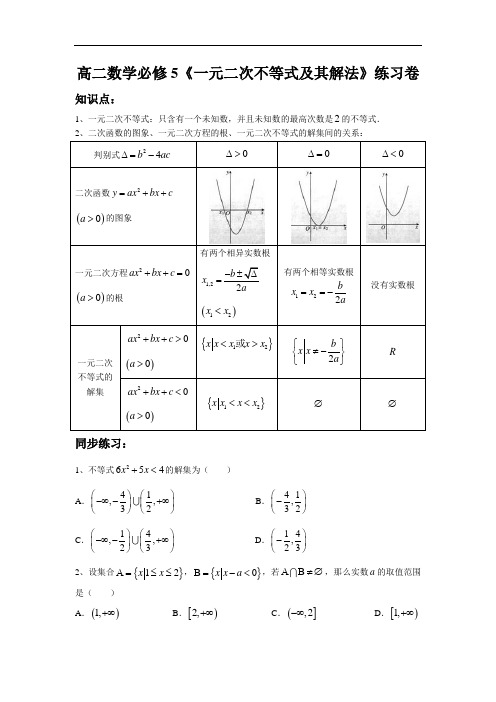
高二数学必修5《一元二次不等式及其解法》练习卷知识点：1、一元二次不等式：只含有一个未知数，并且未知数的最高次数是2的不等式． 判别式24b ac ∆=-0∆> 0∆= 0∆<二次函数2y ax bx c =++()0a >的图象一元二次方程20ax bx c ++=()0a >的根有两个相异实数根1,22b x a-±∆=()12x x <有两个相等实数根122bx x a==-没有实数根一元二次不等式的解集20ax bx c ++>()0a >{}12x x x x x <>或2b x x a ⎧⎫≠-⎨⎬⎩⎭R20ax bx c ++<()0a >{}12x xx x <<∅ ∅同步练习：1、不等式2654x x +<的解集为（ ） A ．41,,32⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ B ．41,32⎛⎫- ⎪⎝⎭C ．14,,23⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ D ．14,23⎛⎫- ⎪⎝⎭2、设集合{}12x x A =≤≤，{}0x x a B =-<，若A B ≠∅，那么实数a 的取值范围是（ ）A ．()1,+∞B ．[)2,+∞C ．(],2-∞D ．[)1,+∞3、若不等式210x mx ++>的解集为R ，则m 的取值范围是（ ） A ．RB ．()2,2-C ．()(),22,-∞-+∞D ．[]2,2-4、设一元二次不等式210ax bx ++>的解集为113x x ⎧⎫-<<⎨⎬⎩⎭，则ab 的值是（ ）A ．6-B ．5-C ．6D ．55、不等式()221200x ax a a --<<的解集是（ ）A ．()3,4a a -B ．()4,3a a -C ．()3,4-D ．()2,6a a 6、不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭，则a b -=（ ） A ．14- B ．14 C ．10- D ．107、不等式222693191122x x x x -+++⎛⎫⎛⎫≤⎪ ⎪⎝⎭⎝⎭的解集是（ ）A ．[]1,10-B ．()[),110,-∞-+∞C ．RD ．(][),110,-∞-+∞8、不等式()()120x x --≥的解集是（ ）A ．{}12x x ≤≤B ．{}12x x x ≥≤或C ．{}12x x <<D ．{}12x x x ><或 9、不等式()20ax bx c a ++<≠的解集为∅，那么（ ）A ．0a <，0∆>B ．0a <，0∆≤C ．0a >，0∆≤D ．0a >，0∆≥10、设()21f x x bx =++，且()()13f f -=，则()0f x >的解集是（ ） A ．()(),13,-∞-+∞ B ．R C ．{}1x x ≠D ．{}1x x =11、若01a <<，则不等式()10a x x a ⎛⎫--> ⎪⎝⎭的解是（ ） A ．1a x a<<B ．1x a a<< C ．x a <或1x a>D ．1x a<或x a >12、不等式()130x x ->的解集是（ ）A ．1,3⎛⎫-∞ ⎪⎝⎭B ．()1,00,3⎛⎫-∞ ⎪⎝⎭ C ．1,3⎛⎫+∞ ⎪⎝⎭D ．10,3⎛⎫ ⎪⎝⎭13、二次函数()2y ax bx c x R =++∈的部分对应值如下表：则不等式20ax bx c ++>的解集是____________________________．14、若0a b >>，则()()0a bx ax b --≤的解集是_____________________________． 15、不等式20ax bx c ++>的解集为{}23x x <<，则不等式20ax bx c -+>的解集是________________________．16、不等式2230x x -->的解集是___________________________． 17、不等式2560x x -++≥的解集是______________________________． 18、()21680k x x --+<的解集是425x x x ⎧⎫<->⎨⎬⎩⎭或，则k =_________． 19、已知不等式20x px q ++<的解集是{}32x x -<<，则p q +=________． 20、不等式30x x +≥的解集为____________________． 21、求下列不等式的解集：⑴ ()()410x x +--<； ⑵ 232x x -+>； ⑶ 24410x x -+>．22、已知不等式220ax bx ++>的解集为1123x x ⎧⎫-<<⎨⎬⎩⎭，求a 、b 的值．23、已知集合{}290x x A =-≤，{}2430x x x B =-+>，求A B ，A B ．。

2018-2019学年高中数学第三章不等式3.2.1 一元二次不等式及其解法课后作业（含解析）新人教A版必修5编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第三章不等式3.2.1 一元二次不等式及其解法课后作业（含解析）新人教A版必修5）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第三章不等式3.2.1 一元二次不等式及其解法课后作业（含解析）新人教A版必修5的全部内容。

第1课时一元二次不等式及其解法1。

不等式9x2+6x+1≤0的解集是（）A. B.C.⌀D。

答案：D2。

不等式〈1的解集是( ）A。

{x｜x>1} B.{x|-1<x<2｝C。

D.解析:原不等式等价于-1〈0⇔〈0⇔（x+1）·（1—2x)<0⇔(2x—1)（x+1)>0,解得x<—1或x>。

答案：C3.函数y=的定义域为( ）A。

｛x｜x≥0｝B。

{x｜x≥1}C.｛x｜x≥1}∪｛0}D.｛x｜0≤x≤1｝解析:要使函数有意义，自变量x的取值需满足解得x≥1或x=0。

答案：C4.已知一元二次不等式ax2+bx+1>0的解集为｛x｜—2<x〈1｝，则a，b的值为( )A。

a=-1,b=—2 B.a=—2，b=—1C.a=b=—D。

a=1，b=2解析:由题知a〈0且—2,1为方程ax2+bx+1=0的两根，由根与系数的关系可求得a=b=—。

答案：C5.若关于x的不等式ax-b>0的解集为(1，+∞）,则关于x的不等式〉0的解集为（)A.（-1，2）B.(—∞,—1)∪(2,+∞)C.(1，2)D.(-∞，—2）∪(1，+∞)解析：因为关于x的不等式ax-b>0的解集为(1,+∞),所以a〉0,且=1,即a=b,所以关于x的不等式>0可化为〉0,其解集是(-∞，—1）∪(2，+∞)。

, [学生用书单独成册])[A.基础达标]1．不等式－x 2－x ＋2≥0的解集是( )A ．{x |x ≤－2或x ≥1}B ．{x |－2＜x ＜1}C ．{x |－2≤x ≤1}D ．∅解析：选C.－x 2－x ＋2≥0⇔x 2＋x －2≤0⇔(x ＋2)(x －1)≤0⇔－2≤x ≤1.2．不等式9x 2＋6x ＋1≤0的解集是( )A.⎩⎨⎧⎭⎬⎫x |x ≠－13B.⎩⎨⎧⎭⎬⎫x |－13≤x ≤13 C ．∅ D.⎩⎨⎧⎭⎬⎫x |x ＝－13 解析：选D.不等式可化为(3x ＋1)2≤0，因此只有x ＝－13，即解集为⎩⎨⎧⎭⎬⎫x |x ＝－13，故选D. 3．设集合S ＝{x ||x |＜5}，T ＝{x |x 2＋4x －21＜0}，则S ∩T ＝( )A ．{x |－7＜x ＜－5}B ．{x |3＜x ＜5}C ．{x |－5＜x ＜3}D ．{x |－7＜x ＜5}解析：选C.因为S ＝{x |－5＜x ＜5}，T ＝{x |－7＜x ＜3}，所以S ∩T ＝{x |－5＜x ＜3}．4．关于x 的一元二次不等式ax 2＋bx ＋c ＜0的解集是全体实数的条件是( ) A.⎩⎪⎨⎪⎧a ＞0Δ＞0 B.⎩⎪⎨⎪⎧a ＞0Δ＜0 C.⎩⎪⎨⎪⎧a ＜0Δ＞0 D.⎩⎪⎨⎪⎧a ＜0Δ＜0 解析：选D.由于不等式ax 2＋bx ＋c ＜0的解集为全体实数，所以，与之相对应的二次函数y ＝ax 2＋bx ＋c 的图像恒在x 轴下方，则有⎩⎪⎨⎪⎧a ＜0，Δ＜0.5．已知0＜a ＜1，关于x 的不等式(x －a )⎝⎛⎭⎫x －1a ＞0的解集为( ) A.⎩⎨⎧⎭⎬⎫x |x ＜a 或x ＞1a B ．{x |x ＞a } C.⎩⎨⎧⎭⎬⎫x |x ＜1a 或x ＞a D.⎩⎨⎧⎭⎬⎫x |x ＜1a 解析：选A.因为0＜a ＜1，所以1a ＞1，即a ＜1a， 所以不等式的解集为⎩⎨⎧⎭⎬⎫x |x ＞1a 或x ＜a . 6．不等式x (3－x )≥x (x ＋2)＋1的解集是________．解析：原不等式即为3x －x 2≥x 2＋2x ＋1，可化为2x 2－x ＋1≤0，由于判别式Δ＝－7＜0，所以方程2x 2－x ＋1＝0无实数根，因此原不等式的解集是∅.答案：∅7．若不等式ax 2＋bx ＋c ＞0的解集为{x |x ＜－2或x ＞4}，对于函数f (x )＝ax 2＋bx ＋c ，则比较f (－1)，f (2)，f (5)的大小为________．解析：因为ax 2＋bx ＋c ＞0的解集为{x |x ＜－2或x ＞4}，所以a ＞0，且对应方程ax 2＋bx ＋c ＝0的两根为x 1＝－2，x 2＝4.所以x 1＋x 2＝－b a ＝2，所以对称轴方程x ＝－b 2a＝1，所以f (－1)＝f (3)且f (2)＜f (3)＜f (5)，所以f (2)＜f (－1)＜f (5)．答案：f (2)＜f (－1)＜f (5)8．下列不等式中：①4x 2＋4x ＋1≥0；②x 2－5x ＋6＞0；③(a 2＋1)x 2＋ax －1＞0.其中解集是R 的是________(把正确的序号全填上)．解析：①⇔(2x ＋1)2≥0⇔x ∈R ；②Δ＝25－4×6＝1＞0.所以②的解集不是R .③Δ＝a 2－4(a 2＋1)×(－1)＝5a 2＋4＞0，所以③的解集不是R ，故填①.答案：①9．解下列不等式：(1)2＋3x －2x 2＞0；(2)x 2－2x ＋3＞0.解：(1)原不等式可化为2x 2－3x －2＜0，所以(2x ＋1)(x －2)＜0.故原不等式的解集是⎩⎨⎧⎭⎬⎫x |－12＜x ＜2. (2)因为Δ＝(－2)2－4×3＝－8＜0，故原不等式的解集是R .10．已知不等式ax 2－3x ＋6＞4的解集为{x |x ＜1或x ＞b }．(1)求a ，b 的值；(2)解不等式ax 2－(ac ＋b )x ＋bc ＜0.解：(1)因为不等式ax 2－3x ＋6＞4的解集为{x |x ＜1或x ＞b }，所以x 1＝1与x 2＝b 是方程ax 2－3x ＋2＝0的两个实数根，b ＞1且a ＞0.由根与系数的关系，得⎩⎨⎧1＋b ＝3a ，1×b ＝2a，解得⎩⎪⎨⎪⎧a ＝1，b ＝2. (2)由(1)知不等式ax 2－(ac ＋b )x ＋bc ＜0可化为x 2－(2＋c )x ＋2c ＜0，即(x －2)(x －c )＜0. 当c ＞2时，不等式(x －2)(x －c )＜0的解集为{x |2＜x ＜c }；当c ＜2时，不等式(x －2)(x －c )＜0的解集为{x |c ＜x ＜2}；当c ＝2时，不等式(x －2)(x －c )＜0的解集为∅.[B.能力提升]1．不等式x 2－|x |－2＜0的解集是( )A ．{x |－2＜x ＜2}B ．{x |x ＜－2或x ＞2}C ．{x |－1＜x ＜1}D ．{x |x ＜－1或x ＞1}解析：选A.令t ＝|x |，则原不等式可化为t 2－t －2＜0，即(t －2)(t ＋1)＜0.因为t ＝|x |≥0，所以t －2＜0，所以t ＜2.所以|x |＜2，得－2＜x ＜2.2．一元二次方程ax 2＋bx ＋c ＝0的根为2，－1，则当a ＜0时，不等式ax 2＋bx ＋c ≥0的解集为( )A ．{x |x ＜－1或x ＞2}B ．{x |x ≤－1或x ≥2}C ．{x |－1＜x ＜2}D ．{x |－1≤x ≤2}解析：选D.由题意知，－b a ＝1，c a＝－2， 所以b ＝－a ，c ＝－2a ，又因为a ＜0，所以x 2－x －2≤0，所以－1≤x ≤2.3．已知2a ＋1＜0，关于x 的不等式x 2－4ax －5a 2＜0的解集是________．解析：因为方程x 2－4ax －5a 2＝0的两个根为x 1＝－a ，x 2＝5a ，又因为2a ＋1＜0，即a ＜－12， 所以x 1＞x 2.故原不等式的解集为{x |5a ＜x ＜－a }．答案：{x |5a ＜x ＜－a }4．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，1，x ＜0，则满足不等式f (1－x 2)＞f (2x )的x 的取值范围是________．解析：由题意有⎩⎪⎨⎪⎧1－x 2＞0，2x ＜0或⎩⎪⎨⎪⎧1－x 2＞2x ，2x ≥0， 解得－1＜x ＜0或0≤x ＜2－1，所以所求x 的取值范围为(－1，2－1)．答案：(－1，2－1)5．解关于x 的不等式：x 2－2ax ＋2≤0.解：因为Δ＝4a 2－8，所以当Δ＜0，即－2＜a ＜2时，原不等式对应的方程无实根，原不等式的解集为∅；当Δ＝0，即a ＝±2时，原不等式对应的方程有两个相等实根．当a ＝2时，原不等式的解集为{x |x ＝2}，当a ＝－2时，原不等式的解集为{x |x ＝－2}；当Δ＞0，即a ＞2或a ＜－2时，原不等式对应的方程有两个不等实根，分别为x 1＝a －a 2－2，x 2＝a ＋a 2－2，且x 1＜x 2，所以原不等式的解集为{x |a －a 2－2≤x ≤a ＋a 2－2}．6．已知不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m }．(1)求t ，m 的值；(2)若函数f (x )＝－x 2＋ax ＋4在区间(－∞，1]上是增加的，求关于x 的不等式log a (－mx 2＋3x ＋2－t )＜0的解集．解：(1)因为不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m }，所以⎩⎪⎨⎪⎧1＋m ＝3，m ＝t ，解得⎩⎪⎨⎪⎧m ＝2，t ＝2. (2)因为f (x )＝－⎝⎛⎭⎫x －a 22＋4＋a 24在(－∞，1]上是增加的， 所以a 2≥1，即a ≥2. 又log a (－mx 2＋3x ＋2－t )＝log a (－2x 2＋3x )＜0.由a ≥2，可知0＜－2x 2＋3x ＜1.由2x 2－3x ＜0，得0＜x ＜32， 由2x 2－3x ＋1＞0，得x ＜12或x ＞1. 所以不等式的解集为⎩⎨⎧⎭⎬⎫x |0＜x ＜12或1＜x ＜32.。

3.2 一元二次不等式及其解法（二）1. 当x＞0时，若不等式x2+ax+1≥0恒成立，则a的最小值为（）A．﹣2 B．﹣3 C．﹣1 D．2. 不等式﹣x2﹣3x+4＞0的解集为．（用区间表示）3. 不等式的解集是．4. 由命题“存在x∈R，使x2+2x+m≤0”是假命题，求得m的取值范围是（a，+∞），则实数a 的值是．5.已知二次不等式ax2+2x+b＞0的解集{x|x}，且a＞b，则的最小值为．6. 如果不等式x2＜|x﹣1|+a的解集是区间（﹣3，3）的子集，则实数a的取值范围是．7. 已知集合M={a，0}，N={x|2x2﹣3x＜0，x∈Z}，如果M∩N≠∅，则a=．8. 已知函数f（x）=x2+（lg a+2）x+lg b满足f（﹣1）=﹣2且对于任意x∈R，恒有f（x）≥2x 成立．（1）求实数a，b的值；（2）解不等式f（x）＜x+5．9. 知不等式|x﹣2|≤1的解集与不等式2x2﹣ax+b＜0的解集相同．（Ⅰ）求a，b的值；（Ⅱ）求函数f（x）=a+b的最大值及取得最大值时x的值．参考答案1. 【解析】当△=a2﹣4≤0，即﹣2≤a≤2时，不等式x2+ax+1≥0对任意x＞0恒成立，当△=a2﹣4＞0，则需，解得a＞2．所以使不等式x2﹣2ax+1≥0对任意x＞0恒成立的实数a的最小值是﹣2．故选：A．2. 【解析】原不等式等价于x2+3x﹣4＜0，所以（x+4）（x﹣1）＜0，所以﹣4＜x＜1；所以不等式的解集为（﹣4，1）；故答案为：（﹣4，1）．3. 【解析】=60，因为底数6＞1，所以指数函数为增函数，则x2+x﹣2＜0即（x﹣1）（x+2）＜0，所以或，解得﹣2＜x＜1，所以不等式的解集为{x|﹣2＜x＜1}故答案为：{x|﹣2＜x＜1}4. 【解析】∵“存在x∈R，使x2+2x+m≤0”是假命题，∴“任意x∈R，使x2+2x+m＞0”是真命题，∴△=4﹣4m＜0，解得m＞1，故a的值是1．故答案为：1．5. 【解析】∵二次不等式ax2+2x+b＞0的解集{x|x}，∴a＞0，且对应方程有两个相等的实根为由根与系数的故关系可得，即ab=1故==（a﹣b）+，∵a＞b，∴a﹣b＞0，由基本不等式可得（a﹣b）+≥2=2，当且仅当a﹣b=时取等号故的最小值为：2故答案为：26. 【解析】不等式x2＜|x﹣1|+a等价为x2﹣a＜|x﹣1|，设f（x）=x2﹣|x﹣1|﹣a，则f（x）=，若不等式x2＜|x﹣1|+a的解集是区间（﹣3，3）的子集，则等价为，即，即，解得a≤5，故答案为：（﹣∞，5]7. 【解析】由N={x|2x2﹣3x＜0，x∈Z}={x|0＜x＜，x∈Z}={1}，又M={a，0}且M∩N≠∅，所以a=1．故答案为1．8. 【解析】（1）由f（﹣1）=﹣2知，lg b﹣lg a+1=0①，所以②．又f（x）≥2x恒成立，f（x）﹣2x≥0恒成立，则有x2+x•lg a+lg b≥0恒成立，故△=（lg a）2﹣4lg b≤0，将①式代入上式得：（lg b）2﹣2lg b+1≤0，即（lg b﹣1）2≤0，故lg b=1即b=10，代入②得，a=100；（2）由（1）知f（x）=x2+4x+1，f（x）＜x+5，即x2+4x+1＜x+5，所以x2+3x﹣4＜0，解得﹣4＜x＜1，因此不等式的解集为{x|﹣4＜x＜1}．9. 【解析】（Ⅰ）不等式|x﹣2|≤1的解集为{x|1≤x≤3}，所以方程2x2﹣ax+b=0的两根为x=1，x=3．∴解得a=8，b=6．（Ⅱ）由（Ⅰ）可知，f（x）=8+6的=4+6，定义域为{x|3≤x≤}．所以（42+62）[（）2+（）2]≥（+6）2，．则f（x）≤3，当且仅当x=时取等号．故当x=时，f（x）的最大值为3.。

学习目标.会解可化为一元二次不等式(组)的简单分式不等式.能够从实际生活和生产中抽象出一元二次不等式的模型，并加以解决.掌握与一元二次不等式有关的恒成立问题的解法．知识点一分式不等式的解法思考>与(－)(＋)>等价吗？将>变形为(－)(＋)>，有什么好处？答案等价；好处是将不熟悉的分式不等式化归为已经熟悉的一元二次不等式．梳理一般的分式不等式的同解变形法则：()⇔>()·()>；()≤⇔(\\(()·()≤；()≠；))()≥⇔≥.知识点二一元二次不等式恒成立问题思考－>在区间上恒成立的几何意义是什么？区间与不等式－>的解集有什么关系？答案－>在区间上恒成立的几何意义是函数＝－在区间上的图象恒在轴上方．区间内的元素一定是不等式－>的解，反之不一定成立，故区间是不等式－>的解集的子集．梳理一般地，“不等式()>在区间上恒成立”的几何意义是函数＝()在区间上的图象全部在上轴方．区间是不等式子集．()>的解集的恒成立的不等式问题通常转化为求最值问题，即：≥()恒成立⇔≥()；⇔()≤恒成立.()≤类型一分式不等式的解法例解下列不等式：()<；()≤.解()<⇔(－)(＋)<⇔－<<，∴原不等式的解集为{－<<}．()∵≤，∴－≤，∴≤，即≥.此不等式等价于(－)≥且－≠，解得<或≥，∴原不等式的解集为.反思与感悟分式不等式的解法：先通过移项、通分整理成标准型>(<)或≥(≤)，再化成整式不等式来解．如果能判断出分母的正负，直接去分母也可．跟踪训练解下列不等式．()≥；()>.解()原不等式可化为(\\((－)(＋)≥，＋≠.))解得(\\(≤－()或≥()，≠－()，))∴<－或≥，∴原不等式的解集为.()方法一原不等式可化为(\\(＋>，－>＋))或(\\(＋<，－<＋.))解得(\\(>－，<－()))或(\\(<－，>－()，))∴－<<－，∴原不等式的解集为.方法二原不等式可化为>，化简得>，即<，∴(＋)(＋)<，解得－<<－.∴原不等式的解集为.类型二不等式恒成立问题例设函数()＝－－.()若对于一切实数，()<恒成立，求的取值范围；()对于∈，()<－＋恒成立，求的取值范围．解()要使－－<恒成立，若＝，显然－<，满足题意；若≠，则(\\(<，,Δ＝＋<))⇒－<<.∴－<≤.()方法一要使()<－＋在∈上恒成立．就要使＋－<在∈上恒成立．。