关于平面电磁波中电场与磁场位相差的讨论

自测题八一、填空题（每题２分，共１０分）１、已知真空中有恒定电流J(r)，则空间任意点磁感应强度B的旋度为。

２、极化方向既不平行也不垂直于入射面的线极化波斜入射在一个无限大介质平面上，__________________时反射波只有平行极化分量。

３、自由空间中原点处的源（ρ或J）在t时刻发生变化，此变化将在时刻影响到ｒ处的位函数（ψ或Ａ）。

４、在球坐标系中，电偶极子辐射场（远场）的空间分布与坐标的关系是_______。

５、已知体积为Ｖ的介质的介电常数为ε，其中的静电荷（体密度为ρ）在空间形成电位分布ψ和电场分布E和D，则空间的静电能量密度为。

空间的总静电能量为________________。

二、选择填空题（每题２分，共１０分，每题只能选择一个答案，否则判为错）1、以下关于时变电磁场的叙述中，不正确的是（）。

A．电场是有旋场B．电场和磁场相互激发C．电荷可以激发电场D．磁场是有源场2、以下关于在导电媒质中传播的电磁波的叙述中，正确的是（）。

A．不再是平面波B．电场和磁场不同相C．振幅不变D．以TE波形式传播3、两个载流线圈之间存在互感，对互感没有影响的是（）。

A．线圈的尺寸B．两个线圈的相对位置C．线圈上的电流D．空间介质4、用镜像法求解静电场边值问题时，判断镜像电荷的选取是否正确的根据是（）。

A．镜像电荷是否对称B．电位ψ所满足的方程是否改变C．边界条件是否改变D．同时选择B和C5、区域V全部用非导电媒质填充，当此区域中的电磁场能量减少时，一定是（）。

A．能量流出了区域B．能量在区域中被损耗C．电磁场做了功D．同时选择A和C自测题八答案J(r)一、1. μ2. θ＝θB3. t＋r／c4. ∝sinθ／r二、1.D 2.B 3.C 4.D 5.A自测题七一、填空题（每题2分，共20分；选择填空题每题只能选择一个答案，否则判为错）1、已知真空中的电荷分布为ρ(r)，则空间任意点电场强度E的散度为_______。

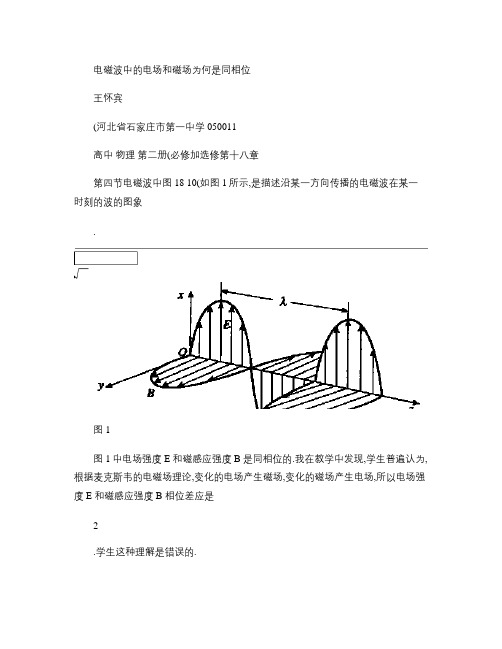
电磁波中的电场和磁场为何是同相位王怀宾(河北省石家庄市第一中学 050011高中物理第二册(必修加选修第十八章第四节电磁波中图18 10(如图1所示,是描述沿某一方向传播的电磁波在某一时刻的波的图象.图1图1中电场强度E 和磁感应强度B 是同相位的.我在教学中发现,学生普遍认为,根据麦克斯韦的电磁场理论,变化的电场产生磁场,变化的磁场产生电场,所以电场强度E 和磁感应强度B 相位差应是2.学生这种理解是错误的.下面我们来分析一下电磁波中的电场强度E 和磁感应强度B 的相位差应该是多少?一、图中所描述的电磁波为平面电磁波,平面电磁波E 和B 同相图1中所示为沿z 轴传播的一定频率的时谐电磁波E (z ,t=E (z e -i tB (z ,t=B (z e -i t代入麦克斯韦方程组!E =- B t , !H = Dt +J ,∀D =!, ∀B =0.因为在自由空间中 !=0,J =0.在一定频率下 D =∀E ,B =#H .所以可得 !E =i B , !H =i D ,∀E =0, ∀H =0.取第一式旋度并用第二式可得!( !E = !i #H =- 2#∀E , !( !E = ( ∀E - 2E=- 2E ,所以麦克斯韦方程组可化为2E +k 2E =0(k =#∀,∀E =0,B =-i!E .第一式又称为亥姆霍兹方程.该图所示为沿z 轴传播的平面电磁波,在此条件下,亥姆霍兹方程化为一维的常微分方程d 2d z2E (z +k 2E (z =0.它的一个解为E (z =e ikz ,则场强的全表达式为E (z ,t=e i (k ∀z - t.平面电磁波的磁场B =-i !E =-iik !E =#∀n !E .由此可知,平面电磁波E 和B 同相位,且都与传播方向垂直.所以认为电场强度E 和磁感应强度B 相位差应是2是错误的.二、学生得出错误结论,源于受电磁振荡模型的影响对于LC 无阻尼振荡回路,由基尔霍夫定∀7∀律可得Ld i d t +qC=0,因d qd t=i,故上式对t 求导,得L d 2i d t 2+i C =0,即d 2i d t 2+ 2i =0,该方程为二阶常系数齐次线性微分方程.该方程的解为i =i m sin ( t +∃.所以电容所带电量 q =#i d t =-i mcos ( t +∃=i m sin ( t +∃+32.可知电容所带电量的相位与回路中电流的相位差2.电感L 具有自感磁能W 磁=12Li 2,电容C 具有电场能W 电=12q 2C ,所以电场能和自感磁能相位差是2.当LC 回路振荡频率比较高,电路开放时,会有效的辐射出电磁能.但是电磁波在回路中的转换过程和电磁波在自由空间的传播过程是截然不同的两个过程,存在不同的物理机制.学生由于定势思维,混淆了这两个过程,得出了错误的结论.参考文献郭硕鸿.电动力学.北京:高等教育出版社,1997 135~142关于电场物质性教学的反思吴怀军(广东省鹤山市第一中学 529700一、教材对电场物质性的描述查阅近几年的高中物理课本,对电场物质性认识的问题上,不同教材略有差异,具体情况是这样的:高中物理读本(必修加选修第二册电场、电场强度一节讲到:电场这种物质跟由分子、原子组成的物质不同,看不见、摸不着,好像不好理解.其实,电场跟其他物质一样,都是不依赖于我们的感觉而客观存在的东西.在一位现代物理学家看来,电场正像他所坐的椅子一样客观存在.电场在跟电荷的相互作用中表现出自己的特性.现行高级中学物理第二册(必修教科书电场强度、电场线一节是这样讲的:电荷周围存在一种叫做电场的物质,电荷通过电场与其他电荷发生作用.高中物理第二册(必修(人教社1995年第二版电场强度、电场线一节中又是这样叙述的:两个电荷相互作用时并不直接接触,它们之间的相互作用也是通过别的物质作媒介而发生的,这种物质就是电场.现行高中物理第二册(必修加选修电场、电场强度一节中又是这样讲的:现在人们已经认识到,电场和磁场虽然跟由分子、原子组成的物质不同,但它们是客观存在的一种特殊物质形态.尽管不同版本、不同时期的教材对电场物质性的描述略有差异,但都说明了电场的这种属性是通过跟电荷的相互作用表现出来.应该说高级中学课本物理第二册(必修(1995年第二版中电场强度、电场线一节对这个问题∀8∀。

第四章 电磁波的传播一、 填空题1、 色散现象是指介质的( )是频率的函数. 答案：,εμ2、 平面电磁波能流密度s 和能量密度w 的关系为( )。

答案：S wv =3、 平面电磁波在导体中传播时,其振幅为( )。

答案：0x E e α-⋅4、 电磁波只所以能够在空间传播,依靠的是( )。

答案：变化的电场和磁场相互激发5、 满足条件( )导体可看作良导体，此时其内部体电荷密度等于( ) 答案：1>>ωεσ, 0, 6、 波导管尺寸为0.7cm ×0.4cm ，频率为30×109HZ 的微波在该波导中能以( )波模传播。

答案： 10TE 波7、 线性介质中平面电磁波的电磁场的能量密度（用电场E 表示）为( )，它对时间的平均值为( )。

答案：2E ε,2021E ε 8、 平面电磁波的磁场与电场振幅关系为( )。

它们的相位( )。

答案：E vB =,相等9、 在研究导体中的电磁波传播时，引入复介电常数='ε( )，其中虚部是( )的贡献。

导体中平面电磁波的解析表达式为( )。

答案： ωσεεi +='，传导电流，)(0),(t x i x e e E t x E ωβα-⋅⋅-= ,10、 矩形波导中，能够传播的电磁波的截止频率=n m c ,,ω( )，当电磁波的频率ω满足( )时，该波不能在其中传播。

若b ＞a ，则最低截止频率为( )，该波的模式为( )。

答案： 22,,)()(b n a m n m c +=μεπω，ω＜n m c ,,ω，μεπb ，01TE11、 全反射现象发生时,折射波沿( )方向传播.答案：平行于界面 12、 自然光从介质1(11με，)入射至介质2(22με，),当入射角等于( )时,反射波是完全偏振波.答案：201n i arctgn = 13、 迅变电磁场中导体中的体电荷密度的变化规律是( ). 答案：0teσερρ-=二、 选择题1、 电磁波波动方程22222222110,0E B E B c t c t∂∂∇-=∇-=∂∂,只有在下列那种情况下成立（ ）A ．均匀介质 B.真空中 C.导体内 D. 等离子体中 答案： A2、 电磁波在金属中的穿透深度（ ）A ．电磁波频率越高,穿透深度越深 B.导体导电性能越好, 穿透深度越深 C. 电磁波频率越高,穿透深度越浅 D. 穿透深度与频率无关 答案： C3、 能够在理想波导中传播的电磁波具有下列特征（ ） A ．有一个由波导尺寸决定的最低频率,且频率具有不连续性 B. 频率是连续的 C. 最终会衰减为零 D. 低于截至频率的波才能通过. 答案：A4、 绝缘介质中，平面电磁波电场与磁场的位相差为（ ）A ．4π B.π C.0 D. 2π答案：C5、 下列那种波不能在矩形波导中存在（ ）A ． 10TE B. 11TM C. mn TEM D. 01TE 答案：C6、 平面电磁波E 、B、k 三个矢量的方向关系是（ ）A ．B E ⨯沿矢量k 方向 B. E B⨯沿矢量k 方向 C.B E ⨯的方向垂直于k D. k E ⨯的方向沿矢量B的方向答案：A7、 矩形波导管尺寸为b a ⨯ ,若b a >,则最低截止频率为（ ）A ．μεπa B. μεπb C.b a 11+μεπ D. a2μεπ答案：A8、 亥姆霍兹方程220,(0)E k E E ∇+=∇⋅=对下列那种情况成立（ ） A ．真空中的一般电磁波 B. 自由空间中频率一定的电磁波C. 自由空间中频率一定的简谐电磁波D. 介质中的一般电磁波 答案：C9、 矩形波导管尺寸为b a ⨯ ,若b a >,则最低截止频率为（ ）A ．μεπa B. μεπb C.b a 11+μεπ D. a2μεπ答案：A三、 问答题1、 真空中的波动方程，均匀介质中的定态波动方程和亥姆霍兹方程所描述的物理过程是什么？从形式到内容上试述它们之间的区别和联系。

电动力学复习题一．填空1．a 、k 及0E 为常矢量，则)]sin([0r k E ⋅⋅∇= , )]sin([0r k E ⋅⨯∇= 。

2．真空中一点电荷电量)sin(0t q q ω=，它在空间激发的电磁标势ϕ为 。

3. 电磁场能流密度的意义是 ，其表达式为 。

4．波矢量αβ i k +=,其中相位常数是 ，衰减常数是 。

5．电容率ε'=ε+i ωσ,其中实数部分ε代表 电流的贡献，它不能引起电磁波功率的耗散，而虚数部分是______电流的贡献，它引起能量耗散。

6. 矩形波导中，能够传播的电磁波的截止频率22,,⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=b n a m n m c μεπω，当电磁波的频率ω满足 时，该波不能在其中传播。

若b >a ，则最低截止频率为 。

7．频率为91030⨯Hz 的微波，在0.7cm ⨯0.4cm 的矩形波导管中，能以 波模传播。

8．爱因斯坦质能关系为 。

如果两事件只能用大于光速的信号进行联系，则这两事件 （填：一定不存在/一定存在/可能存在）因果关系，原因是 是一切相互作用传播的极限速度。

9．电荷守恒定律的微分形式为 ，其物理意义为 ；积分形式为 ，其物理意义为 。

10．a 为常矢量，则=⋅∇)(r a , r a )(∇⋅= 。

12. 磁偶极子的矢势)1(A 等于 ；标势)1(ϕ等于 。

13．B =▽⨯A ,若B 确定，则A ____（填确定或不确定），A 的物理意义是 。

14. 变化电磁场的场量E 和B 与势),(ϕA 的关系是E = ，B = 。

15．库仑规范的条件是 ，在此规范下，真空中变化电磁场的标势ϕ满足的微分方程是 。

16．静电场方程的微分形式为 、 _。

电四极矩有 个独立分量。

17. 半径为0R 、电容率为ε的介质球置于均匀外电场中，则球内外电势1ϕ和2ϕ在介质球面上的边界条件可以表示为 和 。

18．金属内电磁波的能量主要是 能量19．良导体条件为 ；它是由 和 两方面决定的。

关于同相位电磁场位于不同空间点情形的讨论肖军（郑州，黄河科技信息学院）[摘要]本文从三个方面证明了电磁波在传播过程中，同一坐标点处的横向电场和横向磁场的相位是相差2/π，同相位的横向磁场和横向电场是分别位于坐标相差/4λ的两点上。

由此得知，位于同一点处的横向电场和横向磁场能量密度之和为常量，这说明电磁场在传播过程中满足能量守恒定律。

[关键词] 电磁场、横向磁场、横向电场、相位、能量守恒我们知道，若将电磁波传播方向视为纵向，与其垂直方向为横向，对于沿z方向传播的横向电磁场，通过令 ////E E E B B B ⊥⊥=+=+ （1） 由Maxwell 场方程 000000B E t E B t E B εμ∂∇⨯+=∂∂∇⨯-=∂∇⋅=∇⋅= （2） 解出的同相位横向电磁场是()()cos cos E E kz t B B kz t ωω⊥⊥=-=- （3） 这个结果似乎表明，同相位的横向电磁场一定是位于同一坐标点上，其实不然。

位于不同坐标点上的同相位横向电磁场也同样可以满足Maxwell 场方程，下面就从三个方面来讨论。

1、从能量守恒方面考虑以电偶极子辐射的电磁场为例，见图1所示，在闭合环路上的任意点处电偶极子辐射的闭合电场E 的绝对值都相同，而方向是在不断发生改变，若令闭合环路是沿z 方向传播，在闭合环路上的任意点处的电场E 可分解为沿纵向和横向两个分量//E E E ⊥=+ （4）其中沿垂直于z 方向上的横向电场分量是cos()E E kz t ω⊥=- （5）沿平行于z 方向上的纵向电场分量是//sin()E E kz t ω=- （6）显然，在电磁波的传播过程中，E ⊥ 和//E 之间的强度是随着时间t 和传播距离z 的改变而发生周期性变化，但其矢量和始终是等于E 即恒满足于（4）式矢量关系式。

由于横向电场E ⊥ 是与电子运动方向相同，它不能激发磁场，在电磁波传播过程中，它始终是以横向电场形式存在。

关于电磁波中电场和磁场相位差的探讨肖 军由麦克斯韦场方程知道，空间中变化的磁场B 可以在其周围的空间产生变化电场E ，变化的电场E 又在周围空间产生变化磁场B ，这种交替产生的振荡的电场和磁场在空间由远及近传播就是电磁波。

当变化的磁场B 达到最大值0B 时，在其前方空间产生的变化电场E 也同时达到最大值0E ，并满足2200B E εμ=， （1）可见，麦克斯韦方程描述的就是这两个不在同一空间点上的相邻变化电场E 和变化磁场B 之间的变化关系，由于电场E 和磁场B 是在不同的空间点上同时达到最大值，又同时为零，可以断定它们的初相位不同，其初相位差就是在同一空间点处电场a E 和磁场a B 的相位差。

我们知道，在同一空间点处电磁场的能量密度为22001122B w E εμ==（2） 利用（1）式，（2）式可进一步写成形式为2200111222w E E εε⎛⎫=+ ⎪⎝⎭22001111222E B εμ⎛⎫=+ ⎪⎝⎭()()0022001cos 1cos 11222k r t k r t E B ωωεμ⎛⎫-⋅-+⋅-⎪=+ ⎪⎝⎭()()2222000011sin cos 2E k r t B k r t εωωμ⎛⎫=⋅-+⋅- ⎪⎝⎭()()2222000011sin cos 2E k r t B k r t εωωμ⎛⎫=⋅-+⋅- ⎪⎝⎭（3）显然，如果假设电磁场在传播过程中的能量密度是守恒的，在同一空间点处的磁场a B 和电场a E 就一定满足22220011a a E B E B εεμμ+==（4）比较（3）、（4）两式可得到()()()()0000Re e cos Re e cos /2i k r ft a i k r ft a B B B k r ftE E i E k r ft π-⋅--⋅-⎡⎤==⋅-⎢⎥⎣⎦⎡⎤==⋅--⎢⎥⎣⎦（5）这就证明了麦克斯韦方程描述的电场E 和磁场B 不是同相位，而是相差/2π。

电磁波电场与磁场相位的疑惑与通俗演义
电磁波电场与磁场相位疑惑及通俗解释
电磁波电场与磁场相位是电磁学中一个复杂概念，很难用一句话来诠释，有着
许多技术名词和术语被使用。

因此，为了使疑惑告一段落，我们就来为此进行通俗的解释。

首先，电磁波电场是通过空气中的电磁波来传输的，其特性是产生曲线性电场，这与发动机的运行原理有直接关系。

其次，磁场相位是指挥脉冲集群的实际运作，也就是说，它将编码信息传输到远处，从而实现数据传输。

电磁波电场与磁场相位的强度，也就是其大小，则取决于发射机与接收机之间的距离。

电磁波电场与磁场相位一般是由电磁波承载而传播的，其发射可以通过无线电
发射机实现，电磁波传播时其电场与磁场是相互纠缠的，那么就形成了一次高度的变化之后，产生了振荡电磁波，这就是电磁波电场与磁场相位的来源。

电磁波电场与磁场相位的作用也很关键，它主要来源于发射机，像任何一种消
息发射设备，发射机会根据不同的规则，产生指定频率和功率的脉冲信号，从而使得接收机能够按照编出的规则接收到相应的信号，从而，数据便传输到了想要到达的最终位置。

总体而言，电磁波电场与磁场相位是完成无线电传输的关键技术，它们的实现
需要更深入的科学知识和技术，同时也是实现无线电传输的基础。

其实，我们使用的很多设备都与电磁波电场与磁场相位有关，因此，只有了解它们以及新时代所带来的新技术发展，我们才能更好地应用它们，更好地实现无线电传输。

关于高中物理教材中电磁波传播图像中电场与磁场位相的讨论高中物理教材中，关于电磁波的产生是这样描述的：麦克斯韦推断：如果在空间某区域中有周期性变化的电场，那么它就在空间引起变化的磁场；这个变化的磁场又引起新的变化的电场……于是，变化的电场和变化的磁场交替产生，由近及远地向周围传播。

一个伟大的预言诞生了——空间可能存在电磁波。

赫兹证实了麦克斯韦关于光的电磁波理论，赫兹在人类历史上首先捕捉到了电磁波。

教材中还配有电磁波示意图。

如图所示。

（见人民教育出版社2008年6月浙江第2次印刷 普通高中课程标准实验教材物理选修3——4，第78——79页）记得我区有几位物理老师对这个图的画法提出了疑义，他们认为图中电场分量与磁场分量同位相的画法是不对的。

他们认为电场分量与磁场分量应该存在π/2位相差。

根据电磁波产生的原理，若电场随时间的变化式为：那么变化的的电场有如下形式：结论：由变化的电场产生的磁场，应该与电场有π/2位相差。

下面，对这个问题进行讨论：LC振荡电路所产生的电磁场，在空间的分布可分为三个区：近区、远区和过渡区。

产生的电磁波的波长为λ，空间中某点r，三个区域可按r/λ来划分。

r/λ《1，为近区；r/λ》1为远区；r/λ≈1为过渡区。

例如：对于990KHz的无线电波来说，它的波长是λ=c/f=303m，所以r《303m的区域为近区；r》303m的区域为远区。

远区的电磁场特点主要取决于位移电流，即电场变化产生磁场的作用。

在电磁学理论的麦克斯韦方程组中，有一个方程表示了变化的电磁场之间的关系，方程表示式如下：——————————（1）其中称为“磁感应B的旋度”，它描写了磁场随空间的变化率。

在远区，式（1）可以化简为：———————————（2）（2） 表明，从定量上说，电场的时间变化率并不直接与磁场相联系，而是与磁场的空间变化率相联系。

高中教材中说的“电场变化产生磁场；磁场变化产生电场”这句话只是从定性上理解。

关于平面电磁波中电场与磁场位相差的讨论肖军由无场源麦克斯韦方程 2100B E t E B c t E B ∂∇⨯=-∂∂∇⨯=∂∇⋅=∇⋅= . （1） 可解得在真空中一个线偏振的平面电磁波之电场与磁场具有以下函数形式 ()()000i k r t i k r t E E e B B eωωϕ⋅-⋅-+== （2） 式中0E 和0B 都是实数常矢量；k 是波矢量；r 是观测位矢量；ω是角频率；0ϕ是电场E 和磁场B 间的相位差。

由（2）式可推得以下结果()()0i k r t E e E ω⋅-∇⋅=∇⋅ ()0i k r t ik E e ik E ω⋅-=⋅=⋅ (3)()()00i k r t B e B ωϕ⋅-+∇⋅=∇⋅ ()00i k r t ik B e ik B ωϕ⋅-+=⋅=⋅ (4)()()0i k r t E e E ω⋅-∇⨯=∇⨯ ()0i k r t ik E e ik E ω⋅-=⨯=⨯ (5)()()0i k r t E E e t t ω⋅-∂∂=∂∂ ()0i k r t i E e i E ωωω⋅-=-=- (6)()()00i k r t B e B ωϕ⋅-+∇⨯=∇⨯ ()00i k r t ik B e ik B ωϕ⋅-+=⨯=⨯ (7) ()()00i k r t B B e t t ωϕ⋅-+∂∂=∂∂ ()00i k r t i B e i B ωϕωω⋅-+=-=- (8)由此易看出，无论0ϕ是否为零，由(1)式的麦克斯韦场方程均能得到 2k E Bk B E cωω⨯=⨯=- （9） 以及222k c ω= （10）对于00ϕ=情形，电场E 和磁场B 是同相位。

由（2）式知()()00i k r t i k r t E E eB B eωω⋅-⋅-== （11） 上式表明，电场E 和磁场B 均是在t 时刻位于r 点处的电磁场。

对于00ϕ≠情形，电场E 和磁场B 存在有一个位相差0ϕ，若令0k r ϕ=⋅∆ （12）由（2）式可得到 ()()()00i k r t i k r r t E E eB B eωω⋅-⋅+∆-== （13） 上式表明，电场E 是在t 时刻位于r 点处的电场，而磁场B 是在t 时刻位于r r +∆ 点处的磁场，也就是说由麦克斯韦场方程得到的E 和B 已不是同一空间点上的电场和磁场。