第二节 平面简谐波的波动方程

2020高中物理竞赛江苏省苏州高级中学竞赛班上课讲义第九章 机械振动§ 9.2 平面简谐波的波动方程一、平面简谐波波动方程简谐波：如果波源和介质中的各质点都持续地作简谐振动，这种波称为简谐波。

平面简谐波：波面为平面的简谐波。

平面简谐波也称为一维简谐波，其表达式也称波函数(wave function)沿+x 方向传播的一维简谐波 (波速u ，振动角频率为ω)，假设媒质无吸收(质元振幅均为A )介质中任一质点（坐标为 x ）相对其平衡位置的位移（坐标为 y ）随时间的变化关系，即 称为波动方程。

设O 点处质点的振动方程为波线上坐标为x 的任意点P 处质点的振动方程振动从O 点传到P 点所需的时间为t 时刻点 P 的振动与 t-x/u 时刻点O 的振动状态相同，只是落后了Δt 点P 振动方程(,)y x t cos O y A tω=(,)P y f x t ==？x t u∆=cos ()P xy A t uω=-xo任一点p参考点a波速u式中称上式为沿x 轴正向传播的平面简谐波的波动方程波方程的其它表示式讨论：（1）如果原点的初相位不为零设：点 O 振动方程则：波动方程为（2） 如果平面简谐波沿x 轴负方向传播 则 P 点处质点相位比O 点处质点的相位超前波动方程为二、波动方程的物理意义由 从几方面讨论1 当 x 一定时(设x =x 0，即考察波线上某一点x 0) 给出x =x 0处质点的振动方程即x 0处质元的振动表达式，表示x 处的质点在各个不同的时刻位移随时间的变化情况，由它画出的曲线是x 0处质元的振动曲线。

cos 2π()xy A t νλ=-2πων=u λν=[]0cos O y A t ωϕ=+cos[2π()]xy A t νϕλ=-+cos[2π()]xy A t νϕλ=++0cos[2π()]x y A t νϕλ=-+()y y t =2cos()y A t x πωλ=-0cos ()x y A t u ωϕ⎡⎤=-+⎢⎥⎣⎦0cos ()x y A t u ωϕ⎡⎤=++⎢⎥⎣⎦0cos ()x y A t u ωϕ⎡⎤=-+⎢⎥⎣⎦2 当t 一定时(设t = t 0，即在某一时刻t 0)，给出t = t 0时刻各质点的位移y 分布情况反映t 0时刻各不同x 处质元的位移状况，即同一时刻x 轴上各个质点离开它们平 衡位置的位移分布，由它画出的曲线即t 0时刻的波形曲线。

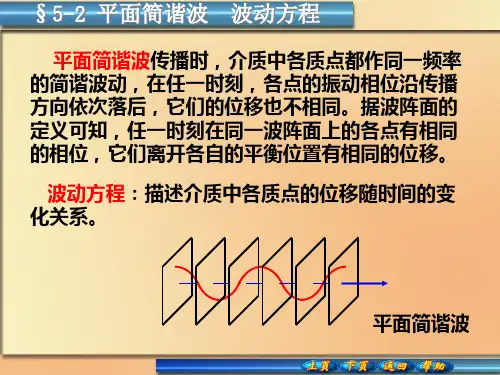
第 2 节平面简谐波一、平面简谐波的描述；二、平面简谐波函数 如果波源做简谐振动，介质中各点也将相继做同频率的简谐振动，这样形成的波叫简谐波。

如果波面为平面，则这样的波称为平面简谐波。

由于平面简谐波的波面上第一点的振动和传播规律完全一样，可以对平面简谐波用一维的方式来处理。

振动相位相差 的两点之间的距离叫波长，常用 表示。

它实际上就是相邻两振动状态相同的点之间的距离。

设一简谐波沿 x 轴方向传播，t 时刻，原点 O 处振动位移的表达式为：在同一时刻 t，到 O 距离为 x 的 P 点的振动表达式与 O 点的振动具有相同的振幅和 频率，但相位比 O 点落后，这是因为 P 点开始振动的时刻比 O 点晚，所晚的时间就是波从O 点传到 P 点所经历的时间，， 称为波的位相速度 ，也称为波速，它表示单位时间某一振动位相所传播的距离，于是 P 点的位移为：这就是简谐波的运动学方程，由于波是向左传播的，又称为右行波，令： 其中 为波长，它表示振动在一个周期中传播的距离。

于是：令：其中， 称为波数，它表示 米内所包含的波长数。

于是简谐波方程可写成：以上各式都是简谐波的方程， 们由波速相互联系，即：是和时间有关的量， 是和空间有关的量，它若 不随 的变化而变化，则称波是无色散的。

简谐波运动学方程的物理意义 ： 波的运动学方程是一个二元函数，位移 y 既是时间 t 的函数，又是位置 x 的函数。

（1）当 x 一定，y 仅为 t 的函数 。

当时，即盯住其一位置看：它表示处的质点随时间做简谐振动，是一个振动方程。

且时刻 t 和 t+T 振动状态相同，说明波动过程在时间上具有周期性，振动的周期、频率、和振幅都与波源相同，但是相位落后：（2）t 一定时，y 仅为 x 的函数，当时：其中，。

此方程表示任意一时刻各质点离开平衡位置位移分布。

可以看出波动过程在空间 上具有周期性，波长就是波动的空间周期。

（3）波表达式的宗量一定，即位相一定，，随着时间 t 的增加，x 也要相应地增加，波必须在空间传播一定的距离，将宗量对时间求微分：其中 为波的位相速度 ，简称相速。

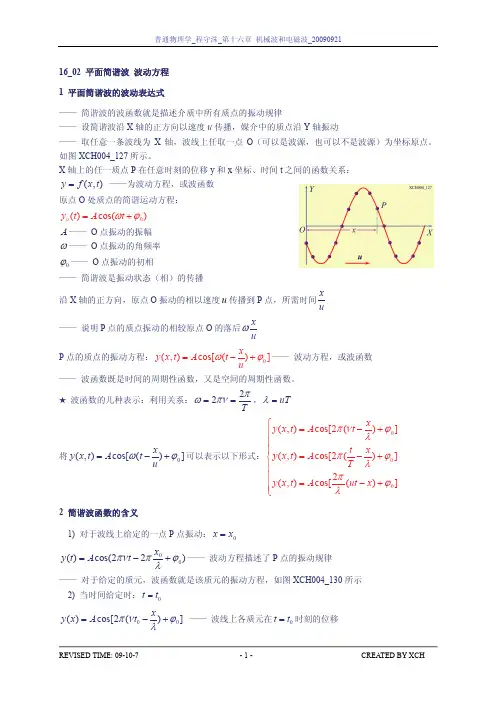
§4-2平面简谐波的波动方程振动与波动最简单而又最基本的波动是简谐波！ 简谐波：波源以及介质中各质点的振动都是简谐振动。

任何复杂的波都可看成是若干个简谐波的叠加。

对平面简谐波，各质点都在各自的平衡位置附近作简谐振动，但同一时刻各质点的振动状态不同。

需要定量地描述出每个质点的振动状态。

波线是一组垂直于波面的平行射线，可选用其中一根波线为代表来研究平面简谐波的传播规律。

一、平面简谐波的波动方程设平面简谐波在介质中沿 x 轴正向传播，在此波线上任取一参考点为坐标原点参考点原点的振动方程为()00cos y A t ωϕ=+任取一点 P ，其坐标为 x ，P 点如何振动？ A 和 ω 与原点的振动相同，相位呢？沿着波的传播方向，各质点的相位依次落后，波每向前传播 λ 的距离，相位落后 2π现在，O 点的振动要传到 P 点，需要向前传播的距离为 x ，因而 P 点的相位比 O 点落后 22x x ππλλ=P 点的振动方程为区别联系振动研究一个质点的运动。

波动研究大量有联系的质点振动的集体表现。

振动是波动的根源。

波动是振动的传播。

x02c o s P y A t x πωϕλ⎛⎫=+- ⎪⎝⎭ 由于 P 点的任意性，上式给出了任意时刻任意位置的质点的振动情况，将下标去掉02c o s y A t x πωϕλ⎛⎫=+- ⎪⎝⎭就是沿 x 轴正向传播的平面简谐波的波动方程。

如果波沿 x 轴的负向传播，P 点的相位将比 O 点的振动相位超前2x πλ沿 x 轴负向传播的波动方程为02c o s y A t x πωϕλ⎛⎫=++⎪⎝⎭利用 2ωπν=， u λν=沿 x 轴正向传播的平面简谐波的波动方程又可写为02c o s y A t x πωϕλ⎛⎫=-+⎪⎝⎭02c o s A t x u πνωϕ⎛⎫=-+⎪⎝⎭0c o s x A t u ωϕ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦即 0c o s x y A t u ωϕ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦原点的振动状态传到 P 点所需要的时间 xt u∆=P 点在 t 时刻重复原点在 x t u ⎛⎫- ⎪⎝⎭时刻的振动状态波动方程也常写为x02c o s y A t x πωϕλ⎛⎫=-+⎪⎝⎭()0c o s A t k x ωϕ=-+ 其中 2k πλ=波数，物理意义为 2π 长度内所具有完整波的数目。

一、平面简谐波的概念平面简谐波是一种特殊的波动现象，它具有特定的波动方程和波动特性。

简谐波的振幅随时间以正弦或余弦函数变化，具有周期性和频率性，是物理学中常见的一种波动形式。

二、平面简谐波的波动方程1. 时间域的波动方程在时间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

2. 空间域的波动方程在空间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

3. 复数形式的波动方程在复数形式下，平面简谐波的波动方程可以表示为：\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的，都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。

它们之间通过变量的不同而具有不同的物理意义，但是描述的是同一种波动现象。

2. 复数形式的波动方程和实数形式的波动方程在复数形式下，简谐波的波动方程可以更加简洁地描述，通过复数的指数函数形式可以很方便地进行波动的运算和分析。

复数形式的波动方程和实数形式的波动方程是等价的，可以相互转化，但在不同的数学和物理背景下有着不同的应用优势。

四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式，广泛应用于物理学、工程学、生物学等领域。

它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值，可以用来描述和分析各种复杂的波动现象。