平面电磁波的波动方程(精选)

电磁场波动方程：宇宙中的震动之声电磁场波动方程是描述电磁波在空间中传播的数学公式。

它不仅是现代物理学的基础，也是人类观测宇宙中“震动之声”的重要手段。

在宇宙中，电磁波是各种星体之间交流信息的主要方式。

例如，从远处的星系中观察可见光波谱，可以告诉我们这些星系的物理属性、组成和运动状态。

类似地，从宇宙空间中捕捉到的微波信号可以揭示宇宙初期的温度分布，雷达信号可以检测近地天体的运动轨迹等。

这些信息均依赖于电磁波的传播和探测技术，其中的核心就是电磁场波动方程。

电磁场波动方程的基本形式是：∇²E - με∂²E/∂t² = 0∇²H - με∂²H/∂t² = 0其中E和H分别表示电场强度和磁场强度，μ和ε分别为真空中的磁导率和电介质常数，∇²表示Laplace算符，∂²/∂t²表示对时间的二阶导数。

这两个方程描述了电场和磁场的演化规律，可以用于计算和预测电磁波在不同介质中的传播方式、速度、波长等物理特性。

电磁场波动方程的研究历史可以追溯到19世纪，当时人们刚刚发现了电和磁的关系，并发现电磁波在真空中以光速传播。

经过不断的理论修正和实验验证，最终得到了现代电磁场波动方程的形式。

这一成就不仅是纯粹科学的进步，还为今后电磁波谱学、计算物理、通信工程等应用领域提供了有力支撑。

总之，电磁场波动方程是探索宇宙奥秘的重要工具，展示了人类对自然界规律精深的认知。

未来，随着技术的不断进步和深入研究，我们相信这一方程仍将为人类发现更多神秘的科学现象和应用价值提供帮助。

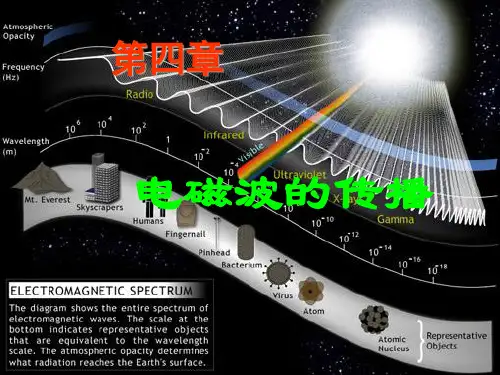
光波的定义光波，通常是指电磁波谱中的可见光。

可见光通常是指频率范围在3.9×1014~7.5×1014Hz之间的电磁波（由于频率数值太大，通常会用波长表示），其真空中的波长约为400~760nm，有些人甚至能感知到380nm-780nm。

光在真空中的传播速度为c=3×108m/s，是自然界中物质运动的最快速度。

（摘自百度百科）光波作为一种特定频段是电磁波，其颜色与频率有关。

可见光中紫光频率最大，波长最短。

红光则刚好相反。

光波的属性光波具有波粒二象性（是指某物质同时具备波的特质及粒子的特质）：也就是说从微观来看，由光子组成，具有粒子性；从宏观来看又表现出波动性。

光波是横电磁波，其中电场强度E和磁感应强度B（或磁场强度H）彼此相互垂直，并且都与传播方向垂直。

注：光的传播形态分类根据传播方向上有无电场分量或磁场分量，可分为如下三类，任何光都可以这三种波的合成形式表示出来。

TEM波：在传播方向上没有电场和磁场分量，称为横电磁波。

TE波：在传播方向上有磁场分量但无电场分量，称为横电波。

TM波：在传播方向上有电场分量而无磁场分量，称为横磁波。

注：横波和纵波分别指的是：波的振动方向与传播方向垂直的波称为横波，电磁波就是横波；波的振动方向和传播方向一致的波叫做纵波，如声波光波的数学描述-波函数(描述光波场（电场）在时间和空间上的分布)波动的特征：波，振动的传播。

振动在空间的传播形成物理量在空间的分布，形成波场。

光波中包含有电场矢量和磁场矢量，从波的传输特性来看，它们处于同样的地位，但是从光与介质的相互作用来看，其作用不同。

在通常应用的情况下，磁场的作用远比电场弱，甚至不起作用。

因此，通常把光波中的电场矢量称为光矢量，把电场E的振动称为光振动，在讨论光的波动特性时，只考虑电场矢量E即可。

波动的最基本特征是具有周期性。

利用麦克斯韦方程表示光波（电场和磁场）和介质的相互作用，得到亥姆霍兹波动方程，通过求解该波动方程得到任意位置传播光波的场1 平面波——一维平面简谐波和三维平面简谐波单色平面波，波只有单一频率w，其振幅和传播方向均不变。

6.2 均匀平面电磁波的概念和特性1、均匀平面电磁波的概念2、时变电磁场的波动方程3、均匀平面波的特性在自由空间，麦克斯韦方程：EH t HE tεμ∂∇⨯=∂∂∇⨯=-∂c v 0,0==J ρ可见：时变的电场可以产生时变的磁场，时变的磁场又可以产生时变的磁电场，同时在空间上向邻近点推移，这样就产生了以一定速度向前传播的电磁波动。

该电磁波动称为电磁波。

什么是电磁波？例如：水波问题：一个点源所发射的电磁波的等相位面是什么样？1、均匀平面电磁波的概念（1）等相位面：在某一时刻，空间具有相同相位的点构成的面称为等相位面。

等相位面又称为波阵面。

（2）球面波：等相位面是球面的电磁波称为球面波。

（3）平面波：等相位面是平面的电磁波称为平面电磁波。

（4）均匀平面电磁波：任意时刻，如果在平面等相位面上，每一点的电场强度均相同，这种电磁波称为均匀平面电磁波。

2、时变电磁场的波动方程从麦克斯韦方程出发：c v 0∂∇⨯=+∂∂∇⨯=-∂∇⋅=∇⋅=DH J t BE tD B ρ在自由空间：HB E D με==0=⋅∇=⋅∇∂∂-=⨯∇∂∂=⨯∇H E tH E t E Hμεc v 0,0==J ρ对第一方程两边取旋度：)(E t H ⨯∇∂∂=⨯∇⨯∇ε()H t t εμ∂∂=-∂∂22Htμε∂=-∂根据矢量运算：22()H H H H∇⨯∇⨯=∇∇⋅-∇=-∇由此可得：222tH H ∂∂=∇με——磁场的波动方程同理可得：222tE E ∂∂=∇με——电场的波动方程3、均匀平面波的特性x yzO对均匀平面波而言，在直角坐标系，假设电磁波沿z 方向传播，等相位面平面平行于xOy 平面。

如图所示：0,0=∂∂=∂∂yx所以：22222222HH z t E Ez tμεμε∂∂=∂∂∂∂=∂∂（1）均匀平面波满足一维波动方程。

（2）均匀平面波是横电磁波（TEM 波）根据麦克斯韦第一方程:tE H ∂∂=⨯∇ε结论：电场只有E x 和E y 分量，说明电场矢量位于xOy 平面上。