平面电磁波的波动方程

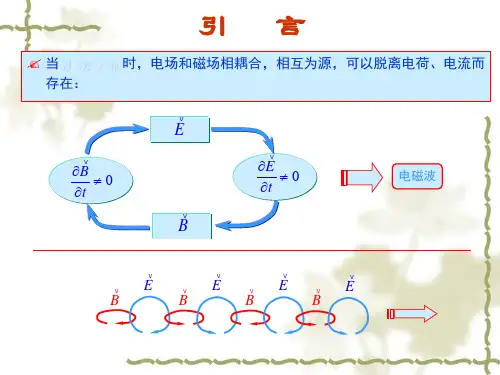
平面电磁波1 时变电磁场以电磁波的形式存在于时间和空间这个统一的物理世界。

2 研究某一具体情况下电磁波的激发和传播规律，从数学上讲就是求解在这具体条件下Maxwell equations 或wave equations 的解。

3 在某些特定条件下，Maxwell equations 或wave equations 可以简化，从而导出简化的模型，如传输线模型、集中参数等效电路模型等等。

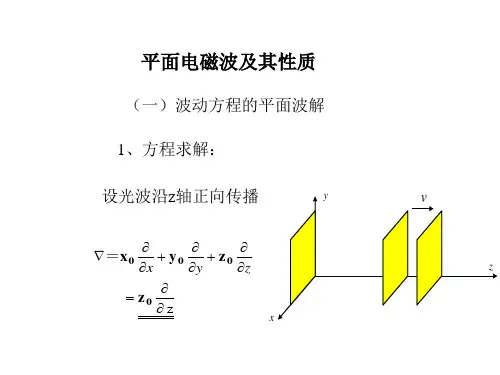
4 最简单的电磁波是平面波。

等相面（波阵面）为无限大平面电磁波称为平面波。

如果平面波等相面上场强的幅度均匀不变，则称为均匀平面波。

5 许多复杂的电磁波，如柱面波、球面波，可以分解为许多均匀平面波的叠加；反之亦然。

故均匀平面波是最简单最基本的电磁波模式，因此我们从均匀平面波开始电磁波的学习。

§ 波动方程1 电场波动方程：ερμμε∇+∂∂=∂∂-∇t J tE E ρρρ222 磁场波动方程 J t H H ρρρ⨯-∇=∂∂-∇222με 2 如果媒质导电（意味着损耗），有E J ρρσ=代入上面，则波动方程变为ερμεμσ∇=∂∂-∂∂-∇222tE t E E ρρρ 0222=∂∂-∂∂-∇tH t H H ρρρμεμσ 如果是时谐电磁场，用场量用复矢量表示，则ερμεωωμσ&&ρ&ρ&ρ∇=+-∇E E j E 22 022=+-∇H H j H &ρ&ρ&ρμεωωμσ 采用复介电常数，εμωωεσμεωωμσμεω&222)1(=-=-j j ，上面也可写成 3 在线性、均匀、各向同性非导电媒质的无源区域，波动方程成为齐次方程。

0222=∂∂-∇tE E ρρμε 0222=∂∂-∇t H H ρρμε 4在线性、均匀、各向同性、导电媒质的无源区域，波动方程成为齐次方程。

0222=∂∂-∂∂-∇tE t E E ρρρμεμσ 0222=∂∂-∂∂-∇tH t H H ρρρμεμσ 如果是时谐电磁场，用场量用复矢量表示，并采用复介电常数，εμωωεσμεωωμσμεω&222)1(=-=-jj ，上面也可写成 022=+∇E E &ρ&&ρεμω 022=+∇H H &ρ&&ρεμω 注意，介电常数是复数代表有损耗。

波动方程及其解法波动方程是常见的偏微分方程之一，它描述的是波的传播和变化。

而在实际问题中，如声波、光波、电磁波等的研究中，波动方程的解法是被广泛使用的。

本文将介绍波动方程的基本概念及其解法。

一、波动方程的基本概念波动方程最基本的形式是一维波动方程，其数学表达式如下：$\frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2 u}{\partial x^2}$其中，$u(x,t)$表示波的位移，$c$是波的速度。

可以看出，波动方程是一个描述时间和空间之间关系的方程。

在这个方程中，偏微分算子表达了波动的传播和变化的规律。

二、波动方程的解法1. 分离变量法分离变量法是解波动方程的最常见方法之一。

其主要思想是，将变量$x$和$t$分离出来，分别让它们满足不同的微分方程。

如一维波动方程可以假设其解为$u(x,t)=X(x)T(t)$，将其代入波动方程可得：$XT''=c^2X''T$进一步变形，可得：$\frac{T''}{c^2T}=\frac{X''}{X}$由此得到两个方程：$\frac{T''}{c^2T}=-\omega^2$$X''=-\omega^2X$其中，$\omega$为角频率，$-\omega^2$为分离出来的常数倍。

对于这两个微分方程，可以分别求解。

2. 叠加原理在叠加原理中，可以将波看做是多个波的叠加。

这种方法可以用于特定场合下的波动方程求解。

例如，在弹性绳的研究中，可以将弹性绳的振动看作是多个波的叠加。

在这种情况下，可以对不同的波求解，并把它们的解加起来成为最终的解。

3. 直接积分法直接积分法是一种基本的解微分方程的方法，同样也适用于波动方程的求解。

在直接积分法中，可以通过对波动方程进行积分，逐步求解出波的变化规律。

这种方法的实现需要考虑初值条件的限制，而条件的不同可能导致问题的复杂性。

一、平面简谐波的概念平面简谐波是一种特殊的波动现象，它具有特定的波动方程和波动特性。

简谐波的振幅随时间以正弦或余弦函数变化，具有周期性和频率性，是物理学中常见的一种波动形式。

二、平面简谐波的波动方程1. 时间域的波动方程在时间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

2. 空间域的波动方程在空间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

3. 复数形式的波动方程在复数形式下，平面简谐波的波动方程可以表示为：\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的，都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。

它们之间通过变量的不同而具有不同的物理意义，但是描述的是同一种波动现象。

2. 复数形式的波动方程和实数形式的波动方程在复数形式下，简谐波的波动方程可以更加简洁地描述，通过复数的指数函数形式可以很方便地进行波动的运算和分析。

复数形式的波动方程和实数形式的波动方程是等价的，可以相互转化，但在不同的数学和物理背景下有着不同的应用优势。

四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式，广泛应用于物理学、工程学、生物学等领域。

它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值，可以用来描述和分析各种复杂的波动现象。

7 平面电磁波的传播从基本方程的微分形式可以看出它们包含了产生电磁场的全部场源信息。

在电磁波中，变化的电场产生变化的磁场，变化的磁场又产生变化的电场，伴随着电场和磁场的传播是能量的传输。

本章从电磁场的基本方程出发，首先介绍电磁波动方程，然后介绍了电磁波中最简单的形态--均匀平面电磁波在理想介质和导电媒质中的情况。

7.1电磁波动方程和平面电磁波变化的电场和变化的磁场之间存在着耦合，这种耦合是以波动的形式存在于空间中。

这种变化的电磁场以波动的存在通常称为电磁波。

电磁波的存在，意味着在空间中有电磁场的变化和电磁能量的传播。

光波、无线电波等都是电磁波，它们在空间不需借助任何媒质就能传播。

7.1.1 一般电磁波动方程设空间为各向同性、线性、均匀媒质，考虑 0=f ρ，0=f J 。

则电磁场基本方程组可写为t∂∂+=⨯∇E E H εγ （7.1.1） t∂∂-=⨯∇H E μ （7.1.2） 0=⋅∇H （7.1.3）0=⋅∇E （7.1.4）对（7.1.1）式两端求旋度()H H H 2∇-⋅∇∇=⨯∇⨯∇()22t t t t ∂∂-∂∂-=⨯∇∂∂+⨯∇=⎪⎭⎫ ⎝⎛∂∂+⨯∇H H E E E E μεγμεγεγ利用（7.1.3）有0222=∂∂-∂∂-∇tt H H H μεγμ （7.1.5） 同理由对（7.1.2）两边取旋度，再代入（7.1.3）、（7.1.2）式等，可推得0222=∂∂-∂∂-∇t t E E E μεγμ （7.1.6） 称上面两式为电磁波动方程（它们是一般性的波动方程）。

我们就是在各向同性、线性、均匀媒质中研究电磁波的基础问题。

H 和E 满足的方程在数学上属同一类方程。

对于电场E 或磁场H 的分量，若用统一的标量符号()t r ,ψ来表示，就可以将原问题转化成标量方程的求解问题0222=∂∂-∂∂-∇t t ψγεψγμψ （7.1.7） 7.1.2 平面电磁波及基本性质对于电磁波传播过程中的某一时刻t ，空间电磁场中E 或H 具有相同相位的点构成的面称为等相面，又称为波阵面。