第三章时域分析法 小结

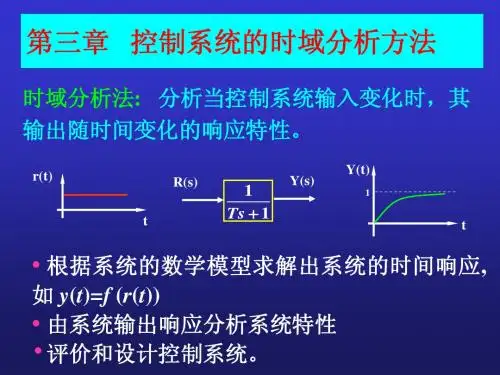
第3章 线性系统的时域分析法所谓时域分析法，就是对系统外施一个给定输入信号，通过研究控制系统的时间响应来评价系统的性能。

由于系统的输出量取的是时间t 的函数，故称这种响应为时域响应，它是一种直接在时间域中对系统进行分析的方法，具有直观、准确、物理概念清楚的特点，尤其适用于二阶系统。

3.1 时域响应及典型输入信号首先我们给出瞬态响应和稳态响应的定义。

瞬态响应——系统在某一输入信号的作用下其输出量从初始状态到稳定状态的响应过程称为瞬态响应，瞬态响应过程也称为过渡过程。

稳态响应——当某一信号输入时，系统在时间趋于无穷大时的输出状态称为稳态响应，稳态也称为静态。

在分析瞬态响应时，我们往往选择典型输入信号。

所谓典型输入信号，是指很接近实际控制系统，经常遇到的输入信号，并在数学描述上经过理想化处理后，用简单的函数形式表达出来的信号。

选择某些典型函数作为系统输入信号，不仅使问题的数学处理系统化，而且典型输入信号的响应往往可以作为分析复杂输入时系统性能的基础。

常见的典型输入信号如下。

1、 阶跃信号这是指输入变量有一个突然的定量变化，例如输入量的突然加入或突然停止等等，如图3-1所示，其数学表达式为⎪⎩⎪⎨⎧<≥=0,00,)(t t a t r （3-1）其中，a 为常数，当a =1时，该信号称为单位阶跃信号。

2、 斜坡信号这是指输入变量是等速度变化的，如图3-2所示，其数学表达式为⎪⎩⎪⎨⎧<≥=0,00,)(t t at t r （3-2）其中，a 为常数，当a =1时，该信号称为单位斜坡信号。

图3-1 阶跃信号 图3-2 斜坡信号3、 脉冲信号脉冲信号的数学表达式可表示为⎪⎩⎪⎨⎧><<<=→000/0,00,lim )(0t t t t t t a t r t （3-3）其中，a 为常数，因此当00t t <<时，该信号值为无穷大。

脉冲信号可以表示为如图3-3所示，其脉冲高度为无穷大；持续时间为无穷小；脉冲面积为a ，因此，通常脉冲强度是以其面积a 衡量的。

第三章 时域分析法时域分析就是根据控制系统的时间响应来分析系统的稳定性，暂态性能和稳态精度。

具有直观和准确的优点，尤其适用于低阶系统。

对控制系统的总要求是稳、准、快。

本章从系统的稳定性、稳态误差和暂态性能方面进行讨论。

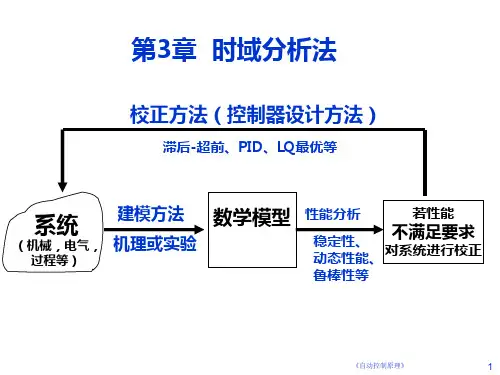
§3-1 时域分析基础一、时域分析法的特点直接解出系统微分方程的时间响应（时域解），根据时间响应的解析式及其曲线图来分析系统的控制性能（稳定性、准确性、快速性等），并找出系统结构、参数与控制性能之间的关系。

时域分析法准确，保有系统响应的全部信息。

二、典型初始状态，典型外作用（典型输入信号）记时间响应为)(t c 。

1. 典型初始状态所谓典型初始状态，即规定控制系统的初始状态均为零状态。

也即当-=0t 时，有0)0()0()0(====--- c cc 。

2. 典型外作用①单位脉冲作用)(t δ：⎩⎨⎧≠=∞=0 ,00,)(t t t δ，⎰+-=001)(dt t δ其拉氏变换式为1)]([=t L δ②单位阶跃作用)(1t ：⎩⎨⎧≥<=0 ,10,0)(1t t t其拉氏变换式为st L 1)](1[=③单位斜坡作用)(1t t ⋅：（等速度函数）⎩⎨⎧≥<=⋅0 ,0,0)(1t t t t t其拉氏变换式为21)](1[s t t L =⋅ ④单位抛物作用)(1212t t ⋅：（等加速度函数）⎪⎩⎪⎨⎧≥<=⋅0 ,210 ,0)(12122t t t t t其拉氏变换式为321)](121[st t L =⋅ 上述各函数间的关系：⑤正弦作用)(1sin t t A ⋅ω：⎩⎨⎧≥<=⋅0 ,sin 0 ,0)(1sin t t A t t t A ωω其拉氏变换式为22)](1sin [ωωω+=⋅s A t t A L系统对不同频率的正弦函数的稳态响应称频率响应。

三、典型时间响应初始状态为零的系统，在典型外作用下的输出，称为典型时间响应。

时域分析方法总结引言时域分析是信号处理领域中常用的一种方法，它的核心思想是对信号在时间上进行观察和分析，从而获取有关信号的时序特征和动态行为。

本文将对时域分析的基本概念和常用方法进行总结和介绍。

时域分析的基本概念时域分析主要依赖于时域信号，即信号在时间轴上的变化。

时域信号是连续的，可以通过采样来离散表示。

常见的时域信号包括周期信号、非周期信号以及随机信号等。

时域分析的目的是通过观察和分析信号在时间上的变化，揭示信号的特征和规律。

常用的时域分析方法1. 时域波形分析时域波形分析是最直观和基本的时域分析方法。

它通过观察信号的波形，分析信号的振幅、频率、周期和相位等特征。

常用的时域波形分析方法包括均方根(RMS) 分析、极值分析和傅里叶级数分析等。

这些方法适用于周期信号和非周期信号的分析。

2. 自相关函数分析自相关函数是用于描述信号与其自身之间的相关性的函数。

自相关函数分析能够揭示信号中的周期性成分和重复模式。

通过计算信号与其延迟后的版本之间的相关性，可以获得自相关函数。

自相关函数分析常用于随机信号的分析和模式识别任务。

3. 相位谱分析相位谱分析是用于分析信号的频率和相位关系的方法。

它通过将信号转换为频域表示，获得信号的频谱信息。

相位谱分析基于信号的频域特性，可以帮助人们理解信号的相位信息、频率成分以及相位偏移等。

常用的相位谱分析方法包括快速傅里叶变换 (FFT) 和功率谱密度分析。

4. 瞬态响应分析瞬态响应分析是用于分析信号对于外部激励的瞬时响应情况。

它通过分析信号在时域上的变化来了解系统的动态行为。

瞬态响应分析常用于分析系统的响应时间、准确性和稳定性等性能指标。

常用的瞬态响应分析方法包括阶跃响应分析和脉冲响应分析。

应用场景时域分析方法在多个领域中都有广泛的应用，包括信号处理、通信、控制系统、生物医学工程等。

时域分析方法可以帮助人们深入了解信号的特性和行为，并根据分析结果进行系统设计、故障诊断、模式识别等工作。

第三章时域分析法3-1 引言前一章中已经叙述过，分析控制系统的第一步是建立物理(实际)系统的数学模型。

一旦系统的数学模型建立起来，就可以采用各种不同的分析方法去分析系统的特性。

如对于线性定常系统，常用的工程方法就是时域分析法、根轨迹法和频率法。

本章讨论时域分析法。

控制系统的动态性能，可以通过在输入信号作用下系统的过渡过程来评价。

系统的过渡过程不仅取决于系统本身的特性，还与外加输入信号的形式有关。

一般情况下，由于控制系统的外加输入信号具有随机的性质而无法预先知道，而且其瞬时函数关系往往又不能以解析形式来表达。

例如火炮控制系统在其跟踪敌机的过程中，由于敌机可以作任意的机动飞行，以致其飞行规律事先无法确定，因此火炮控制系统的输入为一随机信号。

只有在某些特殊情况下，控制系统的输入信号才是确知的。

因此，在分析和设计控制系统时，需要有一个对各种控制系统的性能进行比较的基础，这种基础就是预先规定一些具有特殊型式的试验信号作为系统的输入，然后比较各种系统对这些输入信号的反应。

在控制工程中，常常采用的典型试验信号有阶跃函数、斜坡(速度)函数和脉冲函数等，如图3-1所示。

因为这些信号都是很简单的时间函数，利用这些试验信号，可以容易地对控制系统进行数学和实验的分析。

分析系统特性究竟采用哪一种或哪几种典型输入信号，取决于系统在正常工作情况下，最常见的输入信号形式。

如果控制系统的输入量是随时间逐渐加强的函数，则用斜坡函数是比较合适的。

同样，如果系统的输入信号是突然加入的作用量，则可采用阶跃函数信号；而当系统的输入信号是冲击输入量时，则采用脉冲函数较为合适。

一旦控制系统在试验信号的基础上设计出来后，那么系统对实际输入信号的响应特性，通常也能够满足要求。

利用这些试验信号，人们就能够在同一基础上去比较不同系统的性能。

在这一章中，将讨论系统在非周期信号(阶跃、斜坡和脉冲函数)作用下的响应，如图3-2所示。

关于用正弦试验信号对系统进行分析的问题，将在第五章中进行研究。