当前位置：文档之家 › 第三章控制系统的时域分析法知识点

第三章控制系统的时域分析法知识点

  • 格式：pdf
  • 大小：232.65 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

自动控制原理第三章

自动控制原理第三章


➢ 0 1 特征根： s1,2 n jn 1 2
Xc (s)
1 s
s2
n2 2ns n2
1 s
s2
s 2n 2ns n2
1
s 2n
s (s n )2 (n 1 2 )2
其阶跃输入下的暂态响应：
xc (t) 1
e nt
1 2
sin(n
1 2 t ) , arctan
WB (s)
X c (s) X r (s)
(1
1 K)s
1
1 Ts 1
式中：T 1 k , 称为时间常数。
3.2.2 单位阶跃响应函数：
X r (s) 1 s
11
Xc
(s)
Ts
1
s
,
xc (t)
L1[ 1 Ts 1
1] s
L1[ 1 s
s
1
1
]
1
t
eT
T
xc (t ) xss xtt
2
1.8
1.6
1.4
1.2
1
0.8
0.6 0.4 0.2
0 0
246
nt
8 10 12
⒊ 当 1时，特征方程有一对相等的负实根，称为临界阻尼
系统，系统的阶跃响应为非振荡过程。
➢当 1 时，
阶跃响应曲线为：
xc
(s)
1 s
s2
n2 2n s
n2
n2 s(s n )2
1 1 n s s n (s n )2
1 )( s
T1
1 T2
)
式中
T1
1 a
n (
1
2
1)
控制工程基础：第三章 控制系统的时域分析法

控制工程基础：第三章 控制系统的时域分析法


xo
(t)
d dt
xo1 (t )
xo (t) (1 tet et ) 2et tet
§3.3 二阶系统的时间响应
二阶系统：（凡是能够用二阶微分方程描述的系统）
G(s)
T
2s2
1
2Ts
1
s2
n2 2ns
n2
其中：T 为时间常数，也称为无阻尼自由振荡周期。
称为阻尼比；
n＝1/T 为系统的无阻尼固有频率。
二、一阶系统的单位速度响应
G(s) 1 ， Ts 1
xi (t) t
Xi
(s)
1 s2
Xo(s) G(s)Xi(s)
11 Ts 1 s2
1 s2
T s
T
s
1 T
t
xo (t) t T Te T , t 0
x0 (t)
0
稳态响应：t T 瞬态响应：Tet T
§3.2 一阶系统的时间响应
§3.3 二阶系统的时间响应
X 0 (s)
1 s
(s
s n n )2 d2
1 2
(s
d n )2
d2
xo (t)
1 ent
cosdt
e nt 1 2
sin dt
xo (t) 1
e nt (
1 2
1 2 cosdt sin dt)
xo (t) 1
e nt
1 2
s in(d t
§3.3 二阶系统的时间响应
j
n d
n
n 0
d n
p1,2 n n 2 1
极点实部大于零，响应发散，系统不稳定。
x0 (t) Aent sin(dt )
自动控制原理第3章

自动控制原理第3章

间常数“T”。
12
一阶系统分析
3、单位抛物线响应
y(t)的特点：
y(t)1t2T tT2(1eT t) t0 2
输入与输出之间存在误差为无穷大，这意味着一阶系
统是不能跟踪单位抛物线输入信号的。
4、单位脉冲响应
t
y(t)TeT t0
当 t时， y()0
13
一阶系统分析
对一阶系统典型输入响应的两点说明： 1、输入信号为单位抛物线信号时，输出无法跟踪输入 2、三种响应之间的关系：
38
稳定性分析及代数判据
劳斯判据：
系统稳定的必要条件：特征方程所有系数均为正。
系统稳定的充分条件：特征方程所有系数组成劳斯表，其第 一列元素必须为正。
具体步骤：
1、先求出系统的特征方程
a n S n a n 1 S n 1 a 1 S a n0
注意：
(1) s要降阶排列 (2) 所有系数必须大于0
阶跃响应：
p 2 j1 2 n
Y sss22 n2 n s n2A s1s2 A 2 2 s n s A 3 n
yt 11 12e n t sin 1 2n t
y(t)
ξ=0.3
1
ξ=0.5
20
0
t
二阶系统分析
3、临界阻尼( =1 )
特征根
p1,2 n
阶跃响应：
yt 1 e n t1 n t
42
稳定性分析及代数判据
解：系统闭环特征方程为 s36s25sK0
列劳斯表
s3
1
5
s2
6
K
s 30 K 0
6
s0
K
稳定必须满足
30 K 0 6
《自动控制原理》第三章自动控制系统的时域分析和性能指标

《自动控制原理》第三章自动控制系统的时域分析和性能指标


i1 n
]
epjt
j
(spj)
j1
j1
limc(t) 0的充要条件是 p j具有负实部
t
二.劳斯(Routh)稳定判据
闭环特征方程
a nsn a n 1 sn 1 a 1 s a 0 0
必要条件
ai0. ai0
劳斯表
sn s n1 s n2
| | |
a a n
n2
a a n 1
n3
b1 b2
或：系统的全部闭环极点都在复数平面的虚轴上左半部。
m
设闭环的传递函数：
(s)
c(s) R(s)
k (s zi )
i 1 n
(s p j )
P j 称为闭环特征方程的根或极点 j1
n
(s pj ) 0 称为闭环特征方程
j1
若R(s)=1,则C(s)= s m
k (szi)
n
c(t)L1[c(s)]L1[
t 3、峰值时间 p
误差带
4 、最大超调量
%
C C ( )
% max
100 %
C ( )
ts
5 、调节时间
ts
(
0 . 05
0
.
02
)
6、振荡次N数
e e 7、稳态误差 ss
1C()(对单位阶跃) 输入
ss
第三节 一阶系统的动态性能指标
一.一阶系统的瞬态响应
R(s) -
K0 T 0S 1
s5 | 1 3 2
s4 | 1 3 2
s3 | 4 6
s2
|
3 2
2
s1
|
2 3
s0 | 2
自动控制原理-第3章-时域分析法

自动控制原理-第3章-时域分析法

系统响应达到峰值所需要的时间。
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点
自动控制原理第三章时域分析法

自动控制原理第三章时域分析法

0.135/T 0.05/T 0.018/T
0
T 2T 3T 4T
t
单位脉冲响应曲线
精选课件
19
三.一阶系统的单位斜坡响应 R(t) t, R(s) 1
s2
C(s) (s) R(s) 1 1 1 T T 2
Ts 1 s2 s2 s Ts 1 拉氏反变换，单位斜坡响应为
Ct (t) (t T) Tet/T (t 0) 其中t T为稳态分量，Tet/T为暂态分量。
%h(tp)h( )10% 0
h( )
精选课件
9
超调量表示系统响应过冲的程度，超调量 大，不仅使系统中的各个元件处于恶劣的 工作条件下，而且使调节时间加长。
▪ 五.振荡次数N
在调节时间以内，响应曲线穿越其稳态值 次数的一半。
tr,tp和ts表示控制系统反映输入信号的快速 性，而σ%和N反映系统动态过程的平稳性。 即系统的阻尼程度。其中ts和σ%是最重要
精选课件
20
单位斜坡响应曲线如图所示：
c(t)
r(t)=t
T T
引入误差的概念：0
t
当时间t趋于无穷时，系统单位阶跃响应的实
际稳态值与给定值之差。即：
e hh( )
ss
0 精选课件
21
一阶系统单位斜坡响应存在稳态误差 ess=t-(t-T)=T 从曲线上可知，一阶系统单位斜坡响应达到 稳态时具有和输入相同的斜率，只要在时间 上滞后T,这就存在着ess=T的稳态误差。
c(t) 0 0.63 0.86 0.950 0.98 0.99
1
25
2
3
c(0)1 T
精选课件
14
特点： （1）初始斜率为1/T； （2）无超调 （3）稳态误差ess=0 。
第三章控制系统的时域分析法11

第三章控制系统的时域分析法11


Routh稳定判据
(4)Routh表中第一列元素都是正数 实部为正数的根的个数等于Routh表的第一列元素符号 改变的次数
由此可知e.g.1的(3)是稳定的。
Routh稳定判据的应用
e.g.3 某系统的特征方程为a3S3+a2S2+a1S+a0=0，判 断系统稳定的充要条件。
解: (1) 必要性：ai＞0，i=0,1,2,3
3.1 引言
➢ 传递函数：建立的数学模型
➢ 性能分析：稳定性、动态性能和稳态性能分析
➢ 分析方法：时域分析法、根轨迹法、频域分析法
➢ 时域分析法：直接在时间域中对系统进行分析， 具有直观，准确的优点，可以提供系统时间响应 的全部信息
适用范围
拉氏变换
系统微分方程(t)
传递函数(S)
稳定性
拉氏变换
输入信号(t)
b2
b3
S n3
c1
c2
c3
S n4 d1
d2
d3
S2
e1
e2
S1
f1
S0
g1
Routh稳定判据
Routh计算表的前两行元素由多项式的系数所组成。 从第三行开始，各行元素按下列公式计算：
an an2
b1
an1 an3 an1
an1 an3
c1
b1 b2 b1
b1 b2
d1
c1 c2 c1
(2) 列Routh表如下 S 4 1 3 2 S3 3 3 S2 2 2 S1 0 S0 0 0
？ (3)
Routh稳定判据的应用
Key:如果Routh表第一列元素出现0，则可以用一个小的
正数 代替它，然后继续计算其他元素
自动控制原理第3章

自动控制原理第3章


例1. 系统特征方程式为
s 6 s 12 s 11 s 6 0
4 3 2
例2. 系统特征方程式为
s 3 s 2 s s 5s 6 0
5 4 3 2
特殊情况:
1) 劳斯行列表中某一行左边第一个数为零,其余 不为零或没有. 例: 例:
s 4 3s 3 s 2 3S 1 0
-
1/s
k/(s+5)(s+1)
例:系统特征方程式:
2 s 3 T s 2 10 s 100 0 s
4
按稳定要求确定T的临界值.
六.系统的相对稳定性
§3-3 控制系统的稳态误差
一.误差及稳态误差的定义 系统的误差为 e(t)=被控量的希望值－被控量的实际值 常用的误差定义有两种
二.线性定常系统稳定的充分必要条件
线性定常系统微分方程为:
a0
d dt
n 1
n
n
c (t )
d a dt
1
n 1
c (t ) n 1
d a dt
2
n2 n2
c (t )
d a dt
3
n3 n3
c ( t ) ........
a

d dt
m m
c (t )
a
n
c (t )
第三章 控制系统的时域分析法
§3-1 引言
一. 典型输入信号 1、阶跃函数
r(t)
r (t ) {
0 A
t0 t0
A
t
2、斜坡函数
r(t) {
r(t)
0 At
t0 t0
斜率＝A
朱玉华自动控制原理第3章 时域分析3-1,2,3

朱玉华自动控制原理第3章 时域分析3-1,2,3


1
1
ቤተ መጻሕፍቲ ባይዱ
s4 3s3 s2 3s 1 0 s3 3 3
试判别该系统的稳定性。 s2 0 1
当 0时,3 3 0,
s1 3 3 0
s0
1
有2个特征根在s平面第右3章边控. 制系系统统的是时域不分析稳定的
10 0 0
(2) 劳斯表中某一行的元素全为零。
——这时系统在s平面上存在一些大小相等符号相反的
61
s0 6
劳斯表中第一列元素大于零，所以该系统是稳定的。 这时，系统所有的特征根均处于s平面的左半平面。
第3章 控制系统的时域分析
课程回顾(1)
1、 稳态性能指标 2、 动态性能指标
ess
lim[r(t)
t
cr (t)]
(1)延迟时间td (2)上升时间tr
(3)峰值时间tp
(4)调整时间ts
负可化为全为正） （2）劳斯表中第一列所有元素均大于零。
第3章 控制系统的时域分析
例3-1 已知三阶系统特征方程为 a0s3 a1s2 a2s a3 0
试写出系统稳定的充要条件
解：列写劳斯表 s3
a0
a2
0
s2
a1
a3
0
s1 a1a2 a0a3 0
a1
s0
a3
0
故得出三阶系统稳定的充要条件为：
0
9
s0 5
s1 32
0
s0 5
所得结论不变
第3章 控制系统的时域分析
2、劳斯稳定判据的特殊情况
(1) 劳斯表中某一行的第一个元素（系数）为零，而该 行其它元不为零。
——计算下一行第一个元素时将出现无穷大，以至劳斯 表的计算无法进行。
自动控制原理 第三章时域分析方法

自动控制原理 第三章时域分析方法

位脉冲响应，由此可以求得系统的传递函数。
总结与分析：
一阶系统对典型试验信号的响应 输入信号x(t) 输出响应y(t)
1 2 3
t
1() δ(t)
t T Te t / T
1 et /T
1 T
et /T
l 线性定常系统对输入信号导数的响应，可以通过 把系统对输入信号的响应进行微分求得； l 系统对输入信号积分的响应，可以通过把系统对原 输入信号的响应进行积分求得，而积分常数则由初 始条件决定。
3.1.1 控制系统的输入信号
● 在分析和设计控制系统时，需要有一个对各种
系统性能进行比较的基础。
● 从实际应用中抽象出一些典型的输入信号，它
们具有广泛的代表性和实际意义。
● 通过比较各类系统对这些典型试验信号的响
应来分析它们的性能。
常用的典型试验信号：
r(t) A t (a) 阶跃信号
r(t)
1 E
实验方法求取一阶系统的传递函数：
63.2％ T
1 Ts 1
对一阶系统的单位阶跃响应曲线， 1、直接从达到稳态值的63.2%对应的时间求出一阶 系统的时间常数；
2、从t＝0处的切线斜率求得系统的时间常数。 思考题：
若系统增益K不等于1，系统的稳态值应是多少？如何用实
验方法从响应曲线中求取K值？
3.2.2单位斜坡响应
2、系统的稳态响应为y(∞)=t－T，是一个与输入斜 坡函数斜率相同但时间迟后T的斜坡函数。
3、输出总是小于输入，误差逐步从零增大到时间 常数T并保持不变，因此T也是稳态误差。系统 的时间常数T越愈小，系统跟踪输入信号的稳态 误差也越小。
3.2.3 单位脉冲响应
1 R( s) L[ ( t )] 1 Y ( s) G ( s) R( s) G (s ) Ts 1 系统输出量的拉氏变换式就是系统的传递函数
第 三 章 控制系统的时域分析

第 三 章 控制系统的时域分析


lim c(t) 0
t
反之，若特征根中有一个或多个根具有正实部 时，则暂态响应将随时间的推移而发散，即
lim c(t)
t
这样的系统就是不稳定的。 综上所述，系统稳定的充分必要条件是
系统特征根的实部均小于零，或系统的特征根 均在根平面的左半平面。
三 劳斯判据
设n阶系统的特征方程为 D(s)=a0sn+a1sn-1+…+an-1s+an =a0(s-p1)(s-p2)…(s-pn)=0
本章重点内容
●稳定性的概念、系统稳定的充要条件及稳 定判据
●稳态误差的定义和计算方法 ●控制系统时域性能指标 ●一阶系统和典型二阶系统的阶跃响应
3-1 控制系统的稳定性
一.稳定性的概念
c a
b
b
如小球平衡位置b点,受外界扰动作用,从b
点到 b点 ，外力作用去掉后,小球围绕b点
作几次反复振荡,最后又回到b点,这时小球 的运动是稳定的。
有系数均大于零。
五.系统参数对稳定性的影响
应用代数判据不仅可以判断系统的稳定性，还 可以用来分析系统参数对系统稳定性的影响。
例 系统结构图如图所示，试确定系统稳定时K的 取值范围。
解 系统的闭环传递函数
C(s)
K

R(s) s3 6s2 5s K
其特征方程式为 D(s) s3 6s2 5s K 0
特 征 根 s1,2 1 j2
设线性定常系统的输出信号c(t)对干扰信号n(t) 的闭环传递函数为
f
(s)

C(s) N (s)

K (s z1)(s z2 ) (s p1)(s p2 )

自动控制原理第三章 控制系统的时域分析方法

ln p
( 2%);
2 1 2
N
1.5 1 2
N
N 1.5 ( 5%)
ln p
3.3.4 二阶系统的计算举例
例 3-3-1
二阶系统如图所示，其中 0.6，n 5rad/s。 r(t) 1(t),求tr , t p , ts , p和N。
解 : 1 2 1 0.62 0.8, d n 1 2 5 0.8 4， n 0.6 5 3
tp
d
n
1 2
1 2
Td
3.最大超调（量） p 的计算
p
c(tp ) c() c()
entp
cosdtp
1
2
sin dt p
100%
entp cos
sin 100%
1 2
即
p e / 1 2 100% e cot
4.过渡过程时间 ts 的计算
c(t)位于响应曲线包络线1 ent 内，
c(3T ) 1 e3 0.95, c(4T ) 1 e4 0.982, c() 1
率•
c(0)
1
t
eT
T
t 0
1 T
T为时间常数，1/T为初始斜
3.2.2一阶系统的单位斜坡响应
令r(t)=t,则有R(s) 1/ s 2 可求得输出信号的拉氏变换式
C(s) 1 1 1 T T 2 Ts 1 s 2 s 2 s Ts 1
C(s)
n2
1
s 2 2 n s n2 s
c(t) L1[C(s)]
1.欠阻尼状态（0<ζ<1）
C(s) 1
s 2 n
s (s n jd )(s n jd )
1
s n

chap3控制系统的时域分析法2013

ai 0
劳斯判据
1、列出系统闭环特征方程：
F (s) ansn an1sn1a1s a0 0 上式中所有系数均为实数，并设 an 0
2、按系统闭环特征方程列写劳斯行列表：
sn
an an2 an4
sn1 an1 an3 an5
sn2 b1
b2
b3
sn3 c1
c2
c3
sn4 d1
d2
d3
一、单位阶跃响应：
R(s) 1 s
Y(s) 1 1 T s(Ts 1) s Ts 1
t
y(t) 1 e T
在单位阶跃作用下，一阶系统的输出量随 时间变化曲线为一条指数曲线。
yt
1
0.632
斜率 1 T
y
t
e
t T
0.865 0.950 0.982
0
T 2T 3T 4T
t
响应曲线具有非振荡特征：
t=T, y(t)=0.632;
t=2T, y(t)=0.865;
t=3T, y(t)=0.95;
t=4T, y(t)=0.982;
dy (t )
1 t eT
1
dt
T
t0
T
一阶系统的单位阶跃响应如果以初始 速度等速上升至稳态值1所需的时间应恰 好为T。
一阶系统的阶跃响应没有超调量，故其 时域性能指标主要以Ts来衡量，Ts的长短 反映了系统过程的快慢。
s
例：系统特征方程为 2s3 10s2 13s 4 0
判断系统是否有闭环极点在S的右半平面，并验有几个根在
s=-1的右边。 ROUTH’S TABLE：
s3 2 13 s2 10 4ຫໍສະໝຸດ 将s=z-1代入原方程得：

03第三章 控制系统的时域分析法

16第三章 控制系统的时域分析法一．基本内容1． 了解规定典型输入信号的意义；2． 熟练掌握一阶、二阶系统暂态响应及暂态性能指标的计算；3． 了解高阶系统的组成、阶跃响应及其与闭环零点、极点的关系；掌握闭环主导极点的概念，了解用二阶系统响应近似分析高阶系统性能的方法； 4． 了解系统稳定性的概念，熟练掌握线性定常系统稳定的充要条件及劳斯稳定判据； 5． 了解控制系统稳态误差的定义，熟练掌握稳态误差的计算与分析。

二．重点和难点本章的主要内容是通过研究系统的时域响应去评价系统的性能，即稳定性、暂态性能和稳态性能。

1．控制系统的暂态响应控制系统时间响应的暂态分量即暂态响应。

通常以阶跃响应表征系统的暂态性能。

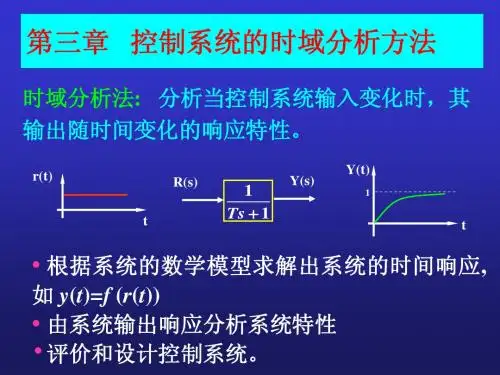
二阶系统的典型传递函数为222222121)()(nn n s s Ts s T S R s C ωζωωζ++=++= 式中 ζ——阻尼比n ω——无阻尼自然振荡角频率，T n 1=ω当10<<ζ时，典型二阶系统的单位阶跃响应为)11sin(111)(222ζζζωζζω-+---=-arctgt et c n tn其单位阶跃响应曲线如图3-1所示 其性能指标：上升时间 21ζωθπ--=n r t （其中ζζθ21-=arctg ,用弧度表示）峰值时间 21ζωπ-=n p t超调量 %10021⨯=--ζζπe M p调节时间 ns t ζω3%)5(≈（或ns t ζω4%)2(≈）17)(t c 1.00.5图3-1典型二阶系统的单位阶跃响曲线对于高阶系统，其暂态响应可以看成是由一阶和二阶系统暂态响应分量组合而成的。

如果系统传递函数中距离虚轴最近的闭环极点，其实部仅有其他极点实部的51或更小一些，并且该闭环极点附近无闭环零点，则可认为系统的响应主要由该极点决定。

这种闭环极点被称为闭环主导极点。

通常系统的主导极点是共轭复数极点，故系统的暂态响应性能也可由相应的二阶系统暂态响应近似估计。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章 控制系统的时域分析法
一、知识点总结
1．掌握典型输入信号（单位脉冲、单位阶跃、单位速度、单位加速度、正弦信号）的拉氏变换表达式。

2．掌握系统动态响应的概念，能够从系统的响应中分离出稳态响应分量和瞬态响应分量；掌握系统动态响应的性能评价指标的概念及计算方法（对于典型二阶系统可以直接应用公式求解，非典型二阶系统则应按定义求解）。

解释：若将系统的响应表达成拉普拉氏变换结果（即S 域表达式），将响应表达式进行部分分式展开，与系统输入信号极点相同的分式对应稳态响应；与传递函数极点相同的分式对应系统的瞬态响应。

将稳态响应和瞬态响应分式分别进行拉氏逆变换即获得各自的时域表达式。

性能指标：延迟时间、上升时间、峰值时间、调节时间、超调量
3．掌握一阶系统的传递函数形式，在典型输入信号下的时域响应及其响应特征；掌握典型二阶系统的传递函数形式，掌握欠阻尼系统的阶跃响应时域表达及其性能指标的计算公式和计算方法；了解高阶系统的性能分析方法，熟悉主导极点的概念，定性了解高阶系统非主导极点和零点对系统性能的影响。

tr
tp
ts
td
4．熟悉两种改善二阶系统性能的方法和结构形式（比例微分和测速反馈），了解两种方法改善系统性能的特点。

5．掌握系统稳定性分析方法：劳斯判据的判断系统稳定性的判据及劳斯判据表特殊情况的构建方法（首列元素出现0，首列出现无穷大，某一行全为0）；掌握应用劳斯判据解决系统稳定裕度问题的方法。

了解赫尔维茨稳定性判据。

6．掌握稳态误差的概念和计算方法；掌握根据系统型别和静态误差系数计算典型输入下的稳态误差的方法（可直接应用公式）；了解消除稳态误差和干扰误差的方法；了解动态误差系数法。

二、相关知识点例题
例1. 已知某系统的方块图如下图1所示，若要求系统的性能指标为：
δδ%=2222%，tt pp=1111，试确定K和τ的值，并计算系统单位阶跃输入下的特征响应量：tt，tt。

图1
解：系统闭环传递函数为：Φ(s)=CC(ss)RR(ss)=KK ss2+(1+KKKK)ss+KK
因此，ωnn=√KK，ζζ=1+KKKK2√KK，
δ%=e−ππππ�1−ππ2⇒ζζ=0.46，
t pp=ππωωdd=1ss⇒ωdd=ωnn�1−ζζ2=3.14 ⇒ωnn=3.54
K=ωnn2=12.53，τ=2ζζωnn−1KK=0.18
t ss=3ζζωωnn=1.84ss
例2．劳斯判据应用的三种特例处理方法及关于稳定度的计算示例（1）劳斯表某行出现全为零的情况：某系统的特征方程为ss5+ss4+3ss3+3ss2+2SS+2=0，试判断系统的稳定性。

解：列出系统的劳斯表如下
S5 1 3 2
S4 1 3 2
S3 0 0
由于S3行出现全为零的情况，劳斯表运算无法进行，此时，可以应用上一行，即S4行所在系数构建辅助方程：Q(s)=ss4+3ss2+2，将辅助方程对S求一阶导数后所得方程（即ddQ(s)ddss=4ss3+6ss）的系数作为行的劳斯表系数继续运算，则劳斯表表示为：
S5 1 3 2
S4 1 3 2
S3 4 6
S2 3/2 2
S1 2/3
S0 2
由于劳斯表首列系数均大于零，所以原系统稳定。

（2）劳斯表某行首个元素为零的情况：某系统特征方程为ss4+2ss3+ss2+2ss+1=0，判断系统的稳定性。

解：解：列出系统的劳斯表如下
S4 1 1 1
S3 2 2 0
S2 0 1
由于S2行出现首个元素为零的情况，劳斯表运算无法进行，此时，可以用无穷小的正数“ε”代替“0”继续运算。

如下所示：
S4 1 1 1
S3 2 2 0
S2ε 1
S1 1-2/ε
S0 1
由于1-2/ε<0，所以劳斯表首列元素出现2次符号变更，因此，原系统不稳定，有2个不稳定根。

（3）劳斯表某行首个元素出现∞的情况：某系统特征方程为ss3−3ss+2=0，分析系统的稳定性情况。

解：根据系统稳定的必要条件，即闭环特征方程各系统必须同号且不缺项，该系统肯定不稳定，但尚需要通过劳斯表判断其不稳定根的个数。

列出劳斯表如下：
S3 1 -3
S2 0 2
S1∞
由于S1所在行出现了∞，所以劳斯表无法继续，此时可通过乘以一个具有负零点因式（即S+a的形式，a>0）的方式重构新的特征方程，例
如，可将原特征方程乘以(S+3)，得到ss4+32ss3−3ss2−7ss+6=0，对此时进行劳斯表判别，结果如下：
S4 1 -3 6
S3 3 -7 0
S2 -2/3 6
S1 20
S0 6
由上可知，原系统有2个不稳定根。

（4）已知某系统的闭环特征方程为：ss3+12ss2+47ss+60=0，试判断系统的所有特征根是否位于s=-2的左侧（即稳定裕度为2）。

应用劳斯判据判断稳定裕度问题可以转变为坐标平移问题，即建立新的坐标系，使s=-2成为新坐标系的纵坐标。

引入新变量S1，令s+2=S1。

则原闭环特征方程可表示为关于S1的方程：SS13+6SS12+11SS1+6=0，列出该方程的劳斯表，判断在新坐标系下是否稳定即可：
S3 1 11
S2 6 6
S1 10
S0 6
可以原系统稳定，即系统的所有特征根是否位于s=-2的左侧。

例3．已知系统的结构图如下图2所示，若系统响应最终以ω=2的频率振荡，试确定系统的参数K和a的值。

图2
解：系统的特征方程为：ss3+aass2+(KK+2)ss+KK+1=0
列出劳斯表如下：
S3 1 K+2
S2 a K+1
S1KK+1−aa(KK+2)
aa
S0 K+1
由题意可知，系统以ω=2的频率振荡，说明出现了虚部为2的纯虚根，根据劳斯表特性，对应S的奇数次项所在行出现了全为零的情况，本题对应S1项所在行全为零。

即KK+1−aa(KK+2)
aa=0（1）
对应的辅助方程为：
aass2+KK+1=0⇒其中复数闭环极点为：ss1,2=±jj�KK+1aa=±jj2即：KK+1aa=4（2）
结合（1）和（2），可求得a=0.75，K=2。

例4．某系统的结构框图如图3所示,为保证系统闭环阻尼比ζ＝0.7，单位斜坡函数响应的稳态误差e ss=0.25，试确定参数K、τ的值。

图3
解：将原系统简化成如下形式
可知系统的开环传递函数为：G(s)=KK ss(ss+KKKK+2)=KK/(KKKK+2)
ss(1KKKK+2ss+1)
根据系统单位斜坡稳态误差要求可得：ee ssss=1KK/(KKKK+2)=KKKK+2KK=0.25 (1)
系统的闭环传递函数为：Φ(s)=KK
ss+(KKKK+2)ss+KK
可知是一个标准的二阶系统，可得关系式：2ζωωnn=KKKK+2,KK=ωωnn2(2) 结合式（1）和式（2）可解得：KK=0.186,KK=31.36。