控制系统的时域分析法(精)

实验5-控制系统时域分析实验目的：1. 掌握控制系统的时域分析方法；2. 熟悉控制系统的基本概念；3. 比较不同控制系统的性能指标，并对其优化。

实验原理：控制系统是由控制器、被控对象和传感器等组成的系统。

它的主要功能是将被控对象的输出值与预期输出值（设定值）进行比较，并根据比较结果对控制器的输出信号进行调整，以实现预期的控制系统动态响应。

系统的状态可以用输入输出关系来表示，通常用系统函数表示，它是输入信号与输出信号的转换函数。

根据系统函数的性质，系统的特性可以分析出来，比如稳态误差、响应时间和阻尼等。

控制系统的时域分析方法主要包括以下内容：1. 稳态误差分析稳态误差是指当控制系统到达稳定状态时，被控对象的输出值与设定值之间的差值。

它是一个反映控制系统偏离设定状态能力的指标。

稳态误差对于不同类型的系统有不同的计算方法，常见的系统类型包括比例控制系统、积分控制系统和派生控制系统。

比例控制系统的稳态误差是：$e_{ss}= \frac {k_p}{1+k_p}, (k_p \neq 0)$派生控制系统的稳态误差是0。

2. 基本响应特性分析一个控制系统的基本响应特性主要包括死区、超调量和稳定时间等。

死区是指当控制器输出的信号在一定范围内时，被控对象的输过不会发生变化。

死区对控制系统的响应时间和稳态误差有很大影响，通常需要根据系统的特点对死区进行调整。

超调量是指被控对象的输出值在达到设定值后，超出设定值的程度。

常见的超调量有百分比超调量和绝对超调量。

3. 阻尼及其影响阻尼是指系统的阻尼比，它是表征系统阻尼程度的一个参数。

阻尼对控制系统的稳定性和性能有很大影响。

当阻尼比为1时，系统的响应最快，但容易出现震荡现象。

阻尼比小于1时，系统的响应相对较慢，但是不会出现震荡现象。

当阻尼比大于1时，系统的响应速度较慢，但相对稳定。

实验步骤：本实验采用MATLAB软件对几种常见的控制系统进行时域分析，具体步骤如下：1. 打开MATLAB软件，新建文件进行编程。

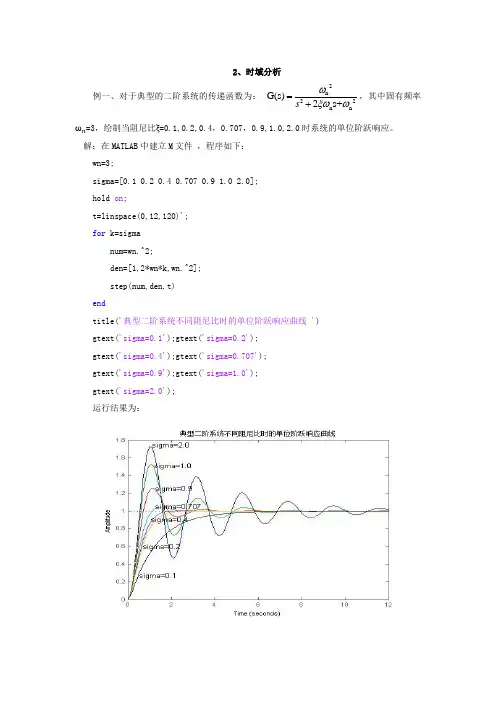
2、时域分析例一、对于典型的二阶系统的传递函数为：2n22n nG(s)2s+sωξωω=+，其中固有频率ωn=3，绘制当阻尼比ξ=0.1,0.2,0.4，0.707，0.9,1.0,2.0时系统的单位阶跃响应。

解：在MATLAB中建立M文件，程序如下：wn=3;sigma=[0.1 0.2 0.4 0.707 0.9 1.0 2.0];hold on;t=linspace(0,12,120)';for k=sigmanum=wn.^2;den=[1,2*wn*k,wn.^2];step(num,den,t)endtitle('典型二阶系统不同阻尼比时的单位阶跃响应曲线 ')gtext('sigma=0.1');gtext('sigma=0.2');gtext('sigma=0.4');gtext('sigma=0.707');gtext('sigma=0.9');gtext('sigma=1.0');gtext('sigma=2.0');运行结果为：分析：由图可见，在ξ=0.4-0.9的范围内，系统上升比较快，且超调量不是很大，故一般工程系统中，ξ就选在这个范围中，其中尤其当ξ=0.707时，响应较快i，此时的超调量为4.31%，通常称其为最佳阻尼，具有最佳阻尼的系统成为二阶最佳系统。

例二、已知连续系统的开环传递函数为：(s5)G(s)50(s3)(s4)s+=++试判断系统闭环的稳定性以及绘制闭环系统的零极点图并作出该系统的单位阶跃响应曲线求出单位阶跃响应稳态误差。

解：（1）判断稳定性方法一：利用roots()函数编制M文件，程序如下：k=50;z=[-5];p=[0 -3 -4];[n1,d1]=zp2tf(z,p,k);P=n1+d1;roots(P)运行结果为：ans =-1.0760 + 7.1000i-1.0760 - 7.1000i-4.8480 + 0.0000i计算结果表明，所有特征根的实部均为负，故闭环系统是稳定的。

第三章 控制系统的时域分析法暂态响应 线性系统的稳定性典型例题分析习题重点内容1． 熟练掌握一阶、二阶系统暂态响应及暂态性能指标的计算； 2． 掌握闭环主导极点的概念， 3． 理解系统稳定性的概念，熟练掌握线性定常系统稳定的充要条件及劳斯稳定判据； 4． 理解控制系统稳态误差的定义，熟练掌握稳态误差的计算与分析。

基本内容1． 了解规定典型输入信号的意义；2． 了解高阶系统的组成、阶跃响应及其与闭环零点、极点的关系；了解用二阶系统响应近似分析高阶系统性能的方法；难点通过研究二阶系统的时域响应去评价系统的性能，即稳定性、暂态性能和稳态性能。

一．暂态响应控制系统时间响应的暂态分量即暂态响应。

通常以阶跃响应表征系统的暂态性能。

1． 一阶系统的暂态响应一阶系统的传递函数为 1Ts 1G(s)+=式中T 称为时间常数，它是表征系统惯性的一个重要参数。

是一个非周期的惯性环节。

单位阶跃响应为 )0(1Y(t)≥-=-t eTt是一条初始值为0，按指数规律上升到稳态值1的曲线，见图3-1。

图3-1 一阶系统的阶跃响应曲线特点：（1）.由于Y(t)的终值为1，因此系统稳态误差为0。

（2）.当t=T 时，Y(T)=0.632。

这表明当系统的单位阶跃响应达到稳态值的63.2%时的时间，就是该系统的时间常数T 。

单位阶跃响应曲线的初始斜率为Te Tt Ttt 11dt dy(t)0===-= 这表明一阶系统的单位阶跃响应如果以初始速度上升到稳态值1，所需的时间恰好等于T 。

性能指标：调节时间为 t s =3T(s) (±5%的误差带) t s =4T(s) (±2%的误差带) 延迟时间为 t d =0.69T(s) 上升时间为 t r =2.20T(s) 峰值时间和超调量都为0。

2． 二阶系统的暂态响应二阶系统的典型传递函数为：222222121)()(nn n s s Ts s T S R s C ωζωωζ++=++= 式中 ζ——阻尼比n ω——无阻尼自然振荡角频率，T n 1=ω当10<<ζ时，典型二阶系统的单位阶跃响应为)11sin(111)(222ζζζωζζω-+---=-arctgt et c n tn其单位阶跃响应曲线如图3-2所示 其性能指标：上升时间 21ζωθπ--=n r t （其中ζζθ21-=arctg ,用弧度表示）峰值时间 21ζωπ-=n p t超调量 %10021⨯=--ζζπe M p调节时间 ns t ζω3%)5(≈（或ns t ζω4%)2(≈）)(t c1.00.5图3-2典型二阶系统的单位阶跃响曲线3． 高阶系统的暂态响应对于高阶系统，其暂态响应可以看成是由一阶和二阶系统暂态响应分量组合而成的。

控制系统时域分析控制系统是指由各种元件和装置组成的，用于控制、调节和稳定各种过程的系统。

在控制系统的设计和分析中，时域分析是一种常用的方法。

时域分析可以通过考察系统输出信号在时间上的变化来评估系统的性能和稳定性。

本文将介绍控制系统的时域分析方法及其在工程实践中的应用。

1. 时域分析的基本概念时域分析是指通过观察系统输入和输出信号在时间轴上的波形变化，来分析控制系统的性能和特性。

在时域分析中，常用的指标包括系统的响应时间、稳态误差、超调量、振荡频率等。

2. 系统的单位阶跃响应单位阶跃响应是指将系统输入信号设置为单位阶跃函数，观察系统输出信号的变化。

单位阶跃响应可以反映系统的动态特性，包括系统的稳态响应和暂态响应。

通过观察单位阶跃响应的波形，可以评估系统的超调量、上升时间、峰值时间等性能指标。

3. 系统的单位脉冲响应单位脉冲响应是指将系统输入信号设置为单位脉冲函数，观察系统输出信号的变化。

单位脉冲响应可以用来确定系统的传递函数和冲激响应。

通过观察单位脉冲响应的波形，可以计算系统的阶跃响应和频率响应等特性。

4. 系统的稳态误差分析稳态误差是指系统输出信号与期望输出信号之间的偏差。

稳态误差分析是用来评估系统在稳态下的性能。

根据系统的稳态误差特性，可以对系统进行进一步的补偿和优化。

通常，稳态误差可以通过单位阶跃响应和传递函数来计算。

5. 系统的波形分析波形分析是指通过观察系统输入和输出信号的波形，来分析系统的性能和特性。

波形分析可以帮助工程师判断系统是否存在超调、振荡和阻尼等问题，从而进行相应的调整和改进。

6. 控制系统的频域分析虽然时域分析是评估控制系统性能的常用方法，但有时候需要使用频域分析来更全面地了解系统的特性。

频域分析可以通过考察系统的频率响应函数来评估系统的稳定性和抗干扰性能。

常见的频域分析方法包括傅里叶变换、拉普拉斯变换和频率响应曲线等。

总结：时域分析是控制系统设计和分析中重要的工具之一。

通过观察系统输入和输出信号在时间上的变化，可以评估系统的性能和稳定性。

实验报告册2020-2021 学年一学期课程名称：MATLAB与控制系统仿真学院：电气工程与自动化学院专业：自动化班级：自动化181学号：1814241145学生姓名：曲嘉宝河南工学院实验报告实验项目控制系统的时域分析法实验日期 2020年11月17日班级自动化181 姓名曲嘉宝指导教师王国柱综合成绩一、预习内容plot(t,y,'b -') grid on xlabel('时间/s'); ylabel('y');title('单位加速度 曲嘉宝'); legend('单位加速度响应曲线')2）已知单位负反馈系统，其开环传递函数为 1102)(21+++=s s s s G 和)3)(2)(1(4)(2++++=s s s s s G ，的串联，系统输入信号为t t r cos )(=，试用Simulink 求取系统输出响应，并将输入输出信号对比显示。

1234567891005101520253035404550时间/sy单位加速度 曲嘉宝单位加速度响应曲线3）已知二阶传递函数为2i)-12i)(s 1(s 10)(+++=s G ，求取单位脉冲响应和用游动鼠标法求取性能指标。

>> z=[]; p=[-1-2*i -1+2i]; k=10; G=zpk(z,p,k); impulse(G)4）已知单位反馈系统，其开环传递函数为)2)(1()(2n n s s s G ζωω++=，其中2=nω，ζ为阻尼比，试绘制ζ分别为0、0.1、0.3、0.5、0.7、0.9时，其单位负反馈教师评阅意见（1）实验预习 (30分)成绩：预习认真、熟练掌握方法与步骤(30～28) □有预习、基本掌握方法与步骤(27～22) 有预习、但未能掌握方法与步骤(21～18) □没有预习，不能完成实验(17～0)（2）操作过程 (40分)成绩：□遵规守纪、操作熟练、团结协作 (40～37) □遵规守纪、操作正确、有协作 (36～29) □遵规守纪、操作基本正确、无协作 (28～24) □不能遵规守纪、操作不正确、无协作(17～0) （3）结果分析 (30分)成绩：□结果详实、结论清晰、讨论合理(30～28) □结果正确、讨论适当(27～22)□结果正确、没有分析讨论(21～18) □结果不正确、没有分析讨论(17～0)其它意见：教师签名：年月日。