自控第三章 时域分析法
- 格式:ppt
- 大小:1.14 MB
- 文档页数:24






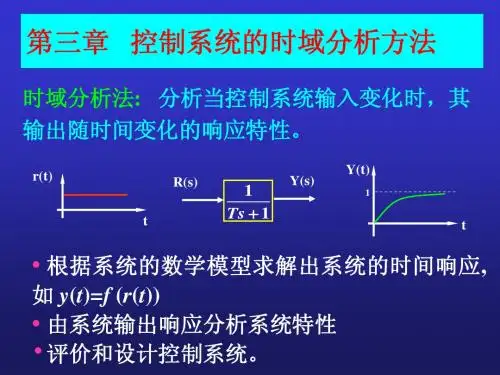
第三章自动控制系统的时域分析法第一节系统的稳定性分析第二节自动控制系统的动态性能分析第三节稳态性能分析第一节系统的稳定性分析一、稳定性的概念定义:线性系统处于某一平衡状态下,受到干扰的作用而偏离了原来的平衡状态,在干扰消失后,系统能够回到原状态或者回到原平衡点附近,称该系统是稳定的,否则,不稳定。
稳定性绝对稳定性:系统稳定(或不稳定)的条件不稳定稳定图3-1稳定性只取决于系统内部的结构和参数,而与初始条件和外作用的大小无关。
二、系统稳定的充分必要条件线性系统特征方程的所有根的实部都必须是负数。
三、Hurwritz代数稳定判据1.Hurwritz代数稳定判据内容设线性系统的特征方程式为:D(s)=an s n+an-1s n-1+……+a2s2+a1s+a=0,则系统稳定的充要条件是:(1)特征方程的各项系数均为正值。
——必要条件(2)特征方程的Hurwritz行列式△k (k=1,2,……n)均大于0。
——充分条件2.Hurwritz行列式△k的编写方法①第一行为特征式第二项、第四项等偶数项的系数;②第二行为特征式第一项、第三项等偶数项的系数;③第三、四行重复上二行的排列,但向右移一列,前一列则用0代替。
其中a a a a a aa a a a a a a n n n n n n n n n 024133142531000000000-------=∆a a a a a n n n n n 2131211----=∆=∆a a a a a a a a n n n n nn n n 314253130-------=∆3.推论在特征方程式各项系数全为正的条件下,若所有奇次Hurwritz 行列式为正,则所有偶次Hurwritz 行列式必为正,反之亦然。
例3-1设系统的特征方程式为2s 4+s 3+3s 2+5s+10=0试判断系统的稳定性.解:(1)各项系数为正,且不为零,满足稳定的必要条件。
(2)系统的Hurritz 行列式为例3-2已知系统的框图如图3-2所示,求当系统稳定时K 的取值范围。