编制计划的原理与方法41页PPT

一教学要求1．理解编制计划的概念、制定计划的原理及计划的特点．2．理解关键路径法的有关概念、关键路线的确定、会根据逻辑关系画出网络图及网络时间的计算．3．了解横道图的概念，会用Excel制作网络图．4．理解单代号网络图与双代号网络图的有关概念及作法．5．理解工程进度的优化、成本优化等计划调整与优化的方法．6．通过本单元教学，培养学生计算技能，计算工具使用技能，数学思维能力和分析与解决问题能力．二教材分析和教学建议(一)编写思路1．教材编写力求从生活中的实际问题引入，通过相关内容的学习，最终回归到引入问题的解决，体现数学来源于生活实际，反之掌握了一定的数学知识和技能就可以解决生活中的一些实际问题．例如，编制计划的有关概念这一节就是从“A胶囊”商业计划书引入的，让学生感受到这章节要编制的计划不同于从前学过和做过的那种计划，通过本节学习后让他们学会编制商业计划书之类的计划．在其他的每个小节里也力求体现这种编写思路．2．数学具有时代性，那么反映数学知识内容的教材更应具有时代性．互联网技术及使用是当今时代的一个重要特征，因此教材编写中力求学生通过互联网技术的使用来学习我们的数学．在本单元中的习题一就要求学生上网查寻相应的编制好了的工作计划．3．将数学知识与计算机应用知识进行适当的整合也是本单元编写的思路之一，所以教材积极地把计算机知识渗透到本单元的各个小节之中．例如用Excel制作横道图，简单、快捷、方便、美观，使学生养成经常使用Excel等软件的习惯和具备使用Excel软件的能力．另外，网络图可以用计算机中应用软件来画，培养学生使用工具软件的能力和认真细致的学习态度．4．本单元的重点内容是关键路径法、网络图．仅管它们作为两个小节来编写的，由于这两方面的知识关联度较大，相互交错性强，所以在编写中难以截然分开，只能相互渗透，各有侧重．在关键路径法这一节中，只是初步认识网络图，教学重点放在对网络图的了解、网络时间的计算和关键路径的确定；在网络图这一节中，教学重点放在单代号和双代号网络图的画法，同时也通过网络图的画法来加深对关键路径法的理解和掌握．而在单代号网络图与双代号网络图的画法的学习中，又侧重于双代号网络图的学习．这两种网络图，如果有一种掌握好了，那另一种掌握起来也就不难了，有触类旁通之感．教材这样安排是为了适当地减轻学生的学习负担，也因为双代号网络图比单代号网络图应用更广泛．5．习题与教材中的例题相匹配，有时这个题是另一个的变式题，这样减少了数量，保证了例题、习题的充分利用，同时使学生可以对一个问题有不同角度的思考，加深对所学知识的全面理解和掌握．(二)课时分配本单元教学时间约需14课时，分配如下(仅供参考)：2．1编制计划的有关概念约2课时2．2关键路径法约3课时2．3横道图约2课时2．4网络图约3课时2．5计划的调整与优化约2课时归纳与总结约2课时(三)内容分析与教学建议2.1编制计划的有关概念1．对于计划的定义要注意以下三点：一是计划是个文本；二是过去学生接触到的计划是行政方面的计划，而现在要学的是企业方面的计划；三是注意两类计划的区别．2．计划概念的引入可用两种方法，一是可以从学生过去做过的计划入手，引申到要学的企业类计划；二是从要学习的计划实际例子出发，进行编制计划的有关概念的教学．教材选择了后一种．3．编制计划的四个原理：对学生来说是比较难理解的，教师应用较多的实例加以说明．特别是学生对灵活性原理和改变航道原理的不同点容易理解不清，这一点，在教学中要加以强调．灵活性原理是计划本身要具有适应性，而改变航道原理是计划执行过程要具有应变能力．限定因素原理有时也被形象地称做“木桶原理”，其意义是指木桶能盛多少水，取决于桶壁上最短的那块板条．许诺原理要求计划必须有期限要求，事实上，在大多数情况下，完成期限是对计划的最严厉的要求．此外，必须合理地确定计划期限，并且不应随意缩短计划的期限．再有，每项计划的许诺不能太多，因为许诺(任务)越多，则计划时间越长，风险越大．灵活性原理就是当出现意外情况时，有能力改变方向而不必花太大的代价．制定计划时要求“量力而行，留有余地”．至于执行计划时，则必须严格准确，要“尽力而为，不留余地”．具有灵活性的计划又称为“弹性计划”，即能适应变化的计划．改变航道原理就是在计划的总目标不变的情形下，但实现目标的进程(即航道)可以因情况的变化随时改变，就象航海一样必须经常核对航线，一旦遇到障碍就可绕道而行．4．计划的分类．计划的分类有多种不同的分法，其中主要的分类方法有如下几种：2.2关键路径法1．构成网络图的要素是实(虚)箭线、节点、路线，它们的叫法较多，三者之间有一定的逻辑关系，且比较抽象，所以进行教学时应多结合实例，让学生从感知认识提升至抽象认识，从而使学生正确理解和掌握网络图中的这三个基本要素．同时要正确了解虚箭线所表示的意义．2．“紧前”与“紧后”表示了网络中的逻辑关系，只有当明确了这种逻辑关系时才能读懂网络图，画对网络图．3图2－1必须要学生熟练掌握，只有这样才能正确掌握网络图．4．在网络图中确定路线，并计算每条路线上单位时间是确定关键路径的方法之一．5．在网络时间的计算中，出现的概念较多，如“作业时间”、“节点的最早开始时间”、“节点的最迟结束时间”、“工序的最早开始时间”、“工序的最迟结束时间”、“时差”、“总时差”等，计算公式看起来也较繁杂，所以学生在学习这方面知识时可能有一定的困难，在教学时要由浅入深、由简到繁，重视和加强练习．2．3横道图1．横道图其实质是一个进度表，在同一张表中可以同时表明计划进度和实际完成的进度，查看横道图可直观地了解计划的落实情况．在工作中是常用的一种图表，我们的学生必须对它们有所了解．2．教材在本节开始时引入四张横道图，主要是让学生了解横道图应用的广泛性，同时增加学生对横道图的感性认识，能较正确地理解横道图的概念．3．横道图有以下三个含义：(1)以图形或表格的形式显示活动；(2)现在是一种通用的显示进度的方法；(3)横轴表示时间，纵轴表示活动(项目)．4．横道图的画法教材中给出了两种，一是手工画横道图，二是用Excel作横道图，重点应掌握用Excel作横道图的方法，这是培养学生“计算工具使用技能和数据处理技能”的一个方面．教师处理这节内容时切不要省略掉用Excel作横道图的内容，而且Excel是数据处理的一个很好的应用软件．用Excel作横道图既简便又美观，所以要适当地增加这方面的练习．2．4网络图1．网络图三个关键元素是：箭线、节点和路线(逻辑关系)，缺一不可．2．本节我们介绍了双代号和单代号两种网络图，要让学生正确理解这两种网络图的有关概念，并了解它们的区别．从定义上看，用箭线表示工作的是双代号网络图，用节点表示图2－2前者是双代号网络图，后者是单代号网络图．3．网络图的分类方法在教材中只给出了两种，其实它们的分类方法不止这两种，还有其他分法，如按层次分类有分级网络计划图，总网络计划图和局部网络计划图；就工作衔接特点分类有普通网络计划图、搭接网络计划图和流水网络计划图等．但不应过多地向学生介绍，因为教学的重点是双代号网络图．4．网络图的画法是本节内容的一个比较重要的方面．目前在数学学科中，作图是职高学生的一个弱项，教学时应适时地跟进必要的例题和练习，让学生较好地掌握这方面的技能，同时培养学生的细心，养成经常动手的习惯，提高学生的鉴赏美的水平，发展学生的逻辑思维能力．网络图的画法必须遵循作法的基本规则：(1)不能出现循环路线；(2)相邻两节点之间只能有一条箭线；(3)自始点起经由任何箭线都可到达终点；(4)一条箭线的中间不允许引出另一条箭线；(5)只能有一个始点和一个终点．画网络图时要注意：(1)网络图的布局要条理清楚，安排整齐，尽量把关键工作和关键路线布置在中心位置，尽可能避免交叉箭线出现；(2)交叉箭线的画法采用一种称为“过桥法”的画法(参见教材图2－16)；(3)事项编号只能从小到大，从左到右，不能重复，编号的顺序是从起点到终点，并且箭头事项的号码必须大于箭尾事项的号码．单代号网络图与双代号网络图的画法主要掌握双代号网络图的画法．5．要让学生会分析相对于某一个作业点(节点)的逻辑关系．6．网络图中有紧前作业、紧后作业、平行作业(平行作业是指能与该作业同时开始的作业)和交叉作业(交叉作业是指能与该作业相互交替进行的作业)等，但交叉作业的概念对学生掌握有一定的难度，所以在教材中没有提出这个概念．2．5计划的调整与优化1．计划是可以优化的．如一个人早上起床后的活动是：刷牙3分钟，洗脸5分钟，做饭9分钟，吃饭7分钟，烧开水10分钟．这五项活动安排可有多种．例如，刷牙—洗脸—做饭—吃饭—烧开水，费时34分钟，但这个计划是可以优化的，如安排成刷牙—洗脸、做饭、烧开水三者同时进行，这样时间将会大大节省．所以任何一个计划都存在着优化问题．2．计划的调整与优化对学生来说是比较难学的一部分内容，而计划的调整与优化所涉及的范围比较大，教材根据中职学生的专业特点，只就工程进度的优化稍作详细的介绍，而工程的成本优化和工程的资源优化只是粗略地介绍．这部分知识学习可以借鉴计算机相关课程中“程序设计的优化”知识的学习．3．工程的进度优化也称工期优化，是指当计算工期不满足要求工期时，可通过压缩关键工作的持续时间来满足工期要求，但在优化过程中不能将关键工作压缩成为非关键工作，优化过程中出现多条关键路线时，必须同时压缩各条关键路线的持续时间，否则不能有效地缩短工期．工期优化的步骤：(1)计算网络计划时间参数，确定关键工作与关键路线．(2)根据计划工期，确定应缩短的时间．(3)把选择的关键工作压缩到最短的持续时间，重新计算工期，找出关键路线．这时要注意不能把关键工作变成非关键工作，若出现多条关键路线时，其总的持续时间应相等．(4)若计算工期仍超过计划工期，则重复上述步骤，直至满足工期要求或工期已不可能再压缩时为止．4．循环法网络优化教材中没作介绍，但为了拓展学生知识面，在习题五中放了一个习题，现将优化的步骤陈述如下：(1)确定初始网络计划的计划工期和关键线路；(2)将计划工期与指令工期比较，求出需要缩短的时间；(3)采用适当的优化措施压缩关键路线的长度，并求出网络计划新的关键路线和工期；(4)若调整后的工期符合规定要求，则优化结束，否则重复(3)直到符合要求为止．5．工程成本最低时的最优工期例子：对图2－3所示的网络计划，进行工期成本优化，寻求最低工程成本下的最优工期．箭线上方数据为该工作的直接费率，箭杆下方括号外为该工作正常持续时间，括号内数据为该工作极限持续时间，间接费率为100元/天．将上面的网络图转化成时标(横向标有时间的)网络图如下：把1－5次时间压缩与总成本减少列表如下：总共减少了320元．。

编制计划的原理与方法在实际的生产、生活、学习中，我们经常会遇到编制计划的问题。

有些问题比较简单，或许你稍作思考就可以给出一个很有“效益”的计划，有些问题比较复杂，需要考虑诸多的干扰因素，例如人力、物力、财力等，这时要想编制一个“合理而高效”的计划是有难度的。

这里我们将学习编制计划的原理与方法，它是一种安排工作进行的数学方法，应用广泛，在企业管理和基本建设中，以及关系复杂的科研项目的组织与管理中，都可以应用。

在本章的学习中，我们将学习编制计划的有关概念，学习分析各项工作之间的逻辑关系，进而掌握编制计划常用的两种图表——网络图与横道图，学会寻找图中的关键路径，进而能够对编制出的计划进行调整和优化。

本章学习目标学完本章内容，你将能够●知道编制计划的有关概念，如节点、紧前工作、紧后工作等●理解关键路径法，会寻求一个计划的关键路径●掌握编制计划常用的两种图表——网络图与横道图●能够对编制的计划进行调整和优化本章目录§1编制计划的有关概念（2课时）§2关键路径法（2课时）§3网络图（1课时）§4横道图（1课时）§5计划的调整与优化（1课时）1编制计划的有关概念（2课时）在日常生活中，我们经常会遇到这样的问题：在人力、物力、财力、时间等条件的限制下，如何为实施计划提供一个可行的方案。

本节将介绍编制计划的有关概念。

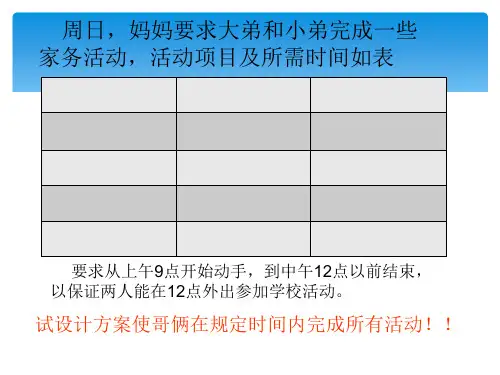
探究某个周日，妈妈要求大弟和小弟完成一些家务活动。

有关活动项目和担任完成活动的要求从上午9点开始动手，到中午12点以前结束，以保证两人能在12点外出参加学校活动。

请你为哥俩设计一份可行的工作计划。

大弟和小弟自己提出了一些方案。

方案1 除了共同用餐外，其他活全部由1人完成。

此时完成任务需要的时间为： 2+1+0.5+0.5=4（小时）此时显然不能完成任务。

方案1不可行。

方案1可用图1所示的示意图表示。

5.05.012−→−−→−−→−−→−DC B A图1方案2 一人收拾房间的同时，另一人做饭，待两人一起完工后，共同用餐，然后一人洗碗。

专题14 编制计划的原理与方法考纲要求一、考点回顾1.工作（工序）、工期、总工期、紧前工作（紧后工作）、平行工作、虚设工作．2.路径工作流程图中，从开始节点沿箭线方向到终止节点的一条线路，叫做一条路径．3.路径的长度一条路径上各工序工期的和叫做路径的长度．4.关键路径长度最长的路径叫做关键路径．5.关键路径上的每一件工作都叫关键工作；关键路径上的每一个节点都叫关键节点；关键路径的长度叫做工程的总工期．6．网络图每一项工作用一条箭线表示，箭线的起点和终点都是编有号码的节点；两个工作间按它们的内在逻辑关系邻接，在表示每一项工作的箭线上方和下方分别标有工作名称和工期．这样的图叫做双代号逻辑网络图，简称网络图．7.制作网络图的基本规则（1）由开始节点出发，按照工作的流向从左到右绘制，直到终止节点．箭线尽量从左至右，避免出现逆向箭线和回路．图中的开始节点和终止节点只能有一个；（2）一项工作有两个节点，两个节点间至多有一条箭线，节点的编号一定要按照箭线的方向由小到大；（3）每一项工作的箭线上方标注工作名称，下方标注工期．虚设工作用虚箭线表示，虚设工作的工期为0.8.编制网络图的基本步骤（1）编排工作明细表，列出各项工作(工序)间的紧前关系；（2）依照工作明细表绘制网络图；（3）节点统一编号．9．横道图又称甘特图 (Gantt chart) ，它是以图示的方式通过活动列表和时间刻度形象地表示出任何特定项目的活动顺序与持续时间．10．横道图绘图注意点（1）左边第一列为工作代码，第二列为工作名称，第三列是工期；（2）用横道表示一项工作和工作的工期，横道的长度表示工期；（3）关键路径上关键工作用红色横道(本书中用黑色代替)表示，非关键工作用斜纹横道表示；（4）表格上方是工程标尺(顺计时)，下方为进度标尺(倒计时)，横道的长度对应于相应工作的开始时间和结束时间．二、基础引领1．做“雪菜肉丝面”有以下几道工序：A.准备肉丝(2分钟)；B.准备雪菜姜丝(1分钟)；C．水加热至沸腾(4分钟)；D.水沸腾后倒入肉丝(3分钟)；E.加入面至沸腾(2分钟)．(1)以下说法错误的是 ( )A．B是D的紧前工作 B．C是D的紧前工作C．B是C的紧前工作 D．D是E的紧前工作(2)以下属于平行工作的是 ( )A．A和D B．A和EC．B和C D．C和E2.某项工程的流程图如下图(单位：h)：第2题图（1）从开始节点①到终止节点⑦有________条路径；（2）关键路径是______________________；（3）完成该工程的最短总工期是________h．3.早饭前，妈妈要进行如下活动：A.烧开水(12分钟)；B.擦桌椅(6分钟)；C.准备暖瓶和灌开水(2分钟)；D.去买早点(6分钟)；E.煮牛奶(8分钟)，其中灶台只有一个火头．(1)试完善整个活动的工作流程图．第2题图(2)妈妈完成这些工作最短需要________．4.某项工作的流程图如下图(单位：天)：第3题图试列出从开始节点①到终止节点⑧的所有路径，指出哪条路径是关键路径，并确定完成该工程的最短总工期．5. 观察某工程的横道图：（1）工程总工期为____(2)该题中，该工程的平行工作是____________________．(3)该题中，该工程的关键工作是____________________．三、典型例题例1．小芳暑期去农村体验生活，她早上起床后有以下家务要做：A.扫地(5分钟)；B.喂鸡(3分钟)；C.淘米(2分钟)；D.洗菜(2分钟)；E.打开炉子(1分钟)；F.煮饭(10分钟)；G.炒菜(8分钟)．(1)试分析以上各项工作之间的先后关系，画出整个活动的工作流程图．(2)试问最短需几分钟完成？类题演练1:小明要骑自行车去超市购买生活物品，外出之前必须做完下面几件事情：A.给自行车打气(2分钟)；B.整理房间(7分钟)；C.穿系鞋带(2分钟)；D.放水并把衣服放进洗衣机(1分钟)；E.洗衣机自动洗涤(12分钟)；F.晾衣服(5分钟)．(1)试画出整个活动的工作流程图．(2)试问最短需几分钟完成？例2．某项工程的流程图如下(单位：天)：(1)试列出从开始节点①到终止节点⑩的所有路径；(2)写出关键路径；(3)求完成该工程的最短总工期．类题演练2：_____某项工程的网络图（单位：天），则该项工程总工期的天数为例3．某工程队承包一项装修工程，包括下列工序：A.整体设计(3月)；B.打地基(2月)；C.订购材料(1月)；D.建筑安装(3月)；E.外墙装修(3月)；F.内部装修(5月)；G.工地清理与验收(1月)．请你根据以上资料：(1)分析各工序之间的关系，设计一份工作流程图；(2)写出从开始节点到终止节点的所有路径，指出哪条是关键路径，并确定最少需要多长时间能完成本工程．例4.填写表中的空缺栏，并绘制出相应的网络图．例5. 某项工程的网络图如图所示(单位：天)．试指出它的关键路径，画出它的横道图．例6．某工程的横道图如图所示：第6题图(1)是确定该工程的关键路径；(2)绘制该工程的网络图.四、巩固训练1．下列关于关键路径的说法正确的是 ( )A．关键路径是从起始节点到终止节点的所有路径中，路长最短的路径B．一个项目的关键路径只有一条C．非关键路径上的工作也可以称为关键工作D．关键路径的长度就是项目的总工期2．祥祥每天早晨冲咖啡经历下列工作：洗水壶(2分钟)，烧水(12分钟)，洗杯子(3分钟)，放好咖啡(1分钟)，则合理安排后所需最少时间为 ( )A．14分钟 B．18分钟 C．15分钟 D．13分钟3.下列网络图的绘制，符合规则的是 ( )A BC D4．关于下面的横道图，说法错误的是 ( )第8题图A．总工期为10天 B．关键路径为A→B→E→DC．A、B、C、D是关键工作 D．C、E间的关系是平行关系5．一个工程的网络图如下图所示，从网络图中分析工序F的紧前工作是( )第9题图A．工序D B．工序C C．工序C，M D．工序C，D6．观察上题的网络图，从开始节点①到终止节点⑩有几条路径（）A．4 B．5 C．6 D．77．已知某工程的工作明细表如下：（1）完成表格（2）试根据该表作出该工程的网络图．（3）画出横道图。