下载文档原格式
第五讲回归设计及统计分析设目标性状y与z1、z2……z m等因素有关，我们可以应用回归分析的方法建立y与诸因素的回归方程,以此对y进行预测和控制，或筛选y的最优指标。
z1、z2……z m构成一个因子空间，每一组z1、z2……z m值对应一个y值。
如何在因子空间中选择最适当的试验点,以最少的试验点寻求y的最优区域，这就要将回归分析与正交设计结合起来应用,称为回归正交设计。
按回归模型的次数,回归正交设计又分为一次回归正交设计和二次回归正交设计。
一、一次回归正交设计一次回归正交设计主要是应用2水平正交表进行设计,其设计和分析步骤如下。
1．确定试验因素的变化范围例如研究m 个栽培因素z 1、z 2……z m 与作物产量y 的数量关系，首先需确定各个栽培因素的变化范围。
设因素z j 的变化区间为（z 1j ，z 2j )，则z 1j 和z 2j 分别为因素z j 的下水平和上水平。
那么1202j jj z z z +=为因素z j 的零水平.212jjj z z ∆=-为因素z j 的变化区间。
2。
对各因素的水平编码编码就是对各个因素的取值作如下线性变换：0j jj jz z x =∆-式中x j 为编码值。
如：10121121212jjj jj j j jjz zz z z x z z =∆-+--==-0000j jj jz z x =∆-=20122221212jjj jj j j jjz zz z z x z z =∆+--==-这样就建立了z j 与x j 的一一对应关系: 下水平 z 1j x 1j （-1）零水平z0j x0j （0 )上水平z0j x0j （+1)通过上面的编码可知，当z j在区间（z1j，z2j)变化时,它的编码值x j就在区间（-1,+1）内变化。
多个因素的编码工作可在因素水平编码表（表1)上进行。
表1 因素水平编码表z j因素Z1Z2……Z m下水平Z11Z12 (1)零水平Z01Z02 0上水平Z21Z22 (2)变化间距△j△1△2……△m对因素的水平进行编码后,y对z1、z2……z m的回归问题就转化为对x1、x2……x m的回归问题。
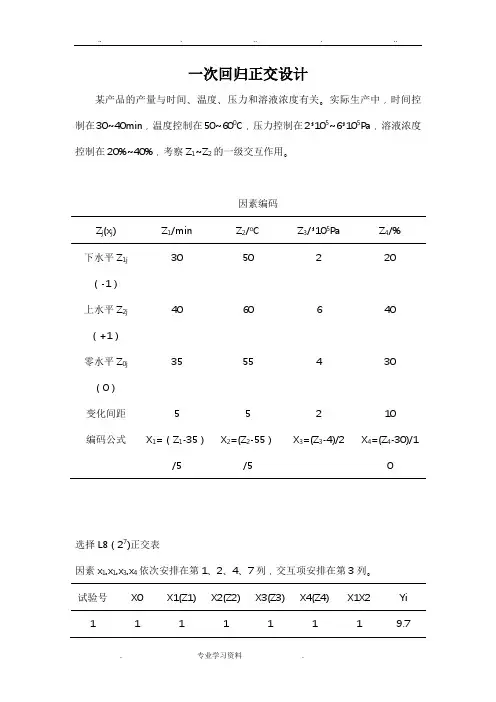
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中，时间控制在30~40min，温度控制在50~600C，压力控制在2*105~6*105Pa，溶液浓度控制在20%~40%，考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j（-1）30 50 2 20上水平Z2j（+1）40 60 6 40零水平Z0j（0）35 55 4 30变化间距 5 5 2 10编码公式X1=（Z1-35）/5 X2=(Z2-55）/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8（27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列，交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验：1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式，该设计最基本的特点是每一个自变量只考虑一次。
这种设计方法可以通过排列组合的方式得到各种不同的设计方案，使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。
一次回归正交设计在实验设计中被广泛使用，尤其在化学制药、工业生产等领域得到了广泛运用。
二次回归正交设计是一种基于一次回归正交设计的设计方式，这种设计方式可以进一步增加实验信息的获取。
在二次回归正交设计中，依然按照一次正交设计的方式来设计实验，但是在每个单独的自变量上，提高对其的测量次数，使得对这些自变量的测量更加准确。
同时，在某些需要深入探究的因素上，可以通过将这些因素的实验次数进一步提高，来获取相关信息。
二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。
在二次回归旋转设计中，实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。
这样可以在保证基本信息获取的同时，增加获取高阶信息的可能性。
旋转设计特别适合于需要同时考虑多个变量的实验设计，可以使各个变量之间更加独立，减少不必要的干扰。
总的来说，在实验设计领域中，三种设计方法各自有着各自的优势。
对于需要更精准的信息获取的实验，应该选择更高阶的设计方法，在更基础的实验中则可以选择更为简单的设计方法。
另外，在选择设计方法的过程中，还应该根据实验具体情况灵活选择，使得实验设计更加科学合理。
三元二次正交回归旋转通用设计在统计学和机器学习领域中，回归分析是一种重要的建模方法，用于探究自变量与因变量之间的关系。
而正交回归是一种特殊的回归方法，它可以解决自变量之间共线性的问题，提高模型的稳定性和可解释性。
本文将介绍三元二次正交回归旋转通用设计方法，以及其在实际应用中的意义和优势。
一、三元二次正交回归在传统的回归分析中，如果自变量之间存在较强的相关性，会导致模型的方差变大，降低模型的预测能力。
而正交回归通过将自变量进行正交化处理，消除它们之间的相关性，从而提高模型的稳定性。
在三元二次正交回归中，通常会将自变量进行二次展开，以更好地捕捉自变量之间的非线性关系。
二、回归旋转回归旋转是一种将原始自变量进行旋转变换的技术，旨在提高模型的解释能力和预测准确性。
通过回归旋转，可以将原始的自变量空间转换为一个新的正交空间，从而使模型更容易解释和理解。
在三元二次正交回归中，回归旋转可以进一步优化模型的设计，提高模型的拟合效果和泛化能力。
三、通用设计三元二次正交回归旋转通用设计是一种灵活而有效的建模方法，适用于各种类型的数据分析和预测问题。
通过将正交回归和回归旋转相结合，可以充分挖掘数据中隐藏的非线性关系，提高模型的拟合效果和预测准确性。
同时，通用设计的特点使得模型具有较强的适应能力，可以应用于不同领域和不同类型的数据集。
四、应用意义三元二次正交回归旋转通用设计在实际应用中具有重要的意义和应用价值。
首先，它可以帮助研究人员更好地理解数据中的复杂关系，揭示隐藏在数据背后的规律和模式。
其次，通过建立高效稳健的模型，可以为决策者提供可靠的决策支持，帮助他们更好地制定策略和规划。
最后，三元二次正交回归旋转通用设计还可以为学术研究和工程实践提供有力的工具和方法，推动科学技术的发展和创新。
三元二次正交回归旋转通用设计是一种强大而灵活的建模方法，具有广泛的应用前景和深远的意义。
通过合理运用这一方法，可以更好地理解和利用数据，为决策和创新提供有力支持，推动社会经济的持续发展。
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中，时间控制在30~40min，温度控制在50~600C，压力控制在2*105~6*105Pa，溶液浓度控制在20%~40%，考察Z1~Z2的一级交互作用。
因素编码Z j (xj) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j（-1）30 50 2 20上水平Z2j（+1）40 60 6 40零水平Z0j（0）35 55 4 30 变化间距 5 5 2 10编码公式X1=（Z1-35）/5 X2=(Z2-55）/5 X3=(Z3-4)/2 X4=(Z4-30)/10选择L8（27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列，交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj211 8 8 8 8 8bj = Bj/aj7.945 0.825 0.325 1.000 1.500 -2.00Qj = Bj2/aj393 5.445 0.845 8.000 18.000 32.000可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验：1、回归系数检验回归关系的方差分析表变异来源SS 平方和 Df 自由度 MS 均方 F 显著水平x 1 5.445 1 5.445 76.25 0.01x 2 0.845 1 0.845 11.83 0.05x 3 8.000 1 8.000 112.04 0.01x4 18.000 1 18.000 252.10 0.01x1x2 32.000 1 32.000 448.18 0.01回归 64.29 5 12.858 180.08 0.01 剩余 0.357 5 0.0714 失拟0.09730.03230.25<1误差e 0.26 2 0.13总和 64.647 10经F 检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。
2、回归方程的检验 进行此项检验时，通常对F 值小于等于1的项不进行检验，直接从回归方程中剔除，对经检验而α>0.25的项，根据实际需要决定是否剔除。
3、失拟检验Lf Lf Lf Lf e e e MS SS df F MS SS df ==由回归系数的检验，回归方程的检验，失拟检验可以得出，产量 y 与各因素之间的总回归关系达到显著，回归方程拟合效果较好。
回归方程的变换将各因素的编码公式代入，得Y=-162.05+4.57z1+2.87z2+0.50z3+0.15z4-0.08z1z2二次回归正交设计某食品加香试验，3个因素，即 Z1(香精用量)、 Z2(着香时间) 、 Z2(着香温度)(1) 确定γ值、 mc 及 m0 。
根据本试验目的和要求，确定 mc＝ 2 m ＝ 2 3＝ 8 ， m0 ＝1 ，查表得γ＝1.215。
(2)确定因素的上、下水平，变化间距以及对因子进行编码编码Z1/(mL／kg物料)Z2 / h Z3/ ℃+γ182448+ 116.9422.645.70121635- 17.069.424.3-γ6822Δi 4.94 6.610.7计算各因素的零水平：Z01 ＝(18＋6)/2＝12 (mL/kg)Z02 ＝(24＋8)/2＝16 (h)Z03 ＝(48＋22)/2＝35 (℃)计算各因素的变化间距：Δ01 ＝(18-12)/1.215＝4.94 (mL/kg)Δ02 ＝(24-16)/1.215＝6.6 (h)Δ03 ＝(48-35)/1.215＝10.7 (℃)(3)列出试验设计及试验方案试验号试验设计实施方案x0x1x2香精用量／(mL／kg)着香时间／h着香温度/ ℃111116.9422.645.7 211-116.9422.624.3 31-1116.949.445.7 41-1-116.949.424.35-1117.0622.645.7 6-11-17.0622.624.3 7-1-117.069.445.7 8-1-1-17.069.424.3 9 1.21500181635 10-1.2150061635 110 1.2150122435 120-1.215012835 1300 1.215121648 1400-1.215121622 150********试验结果的统计分析建立回归方程试验号 0x1x 2x 3x 21x x 31x x 32x x 1x ' 2x ' 3x ' 结果（y ） 1 11 1 1 1 1 1 0.27 0.27 0.27 2.322 1 1 1 -1 1 -1 -1 0.27 0.27 0.27 1.253 1 1 -1 1 -1 1 -1 0.27 0.27 0.27 1.934 1 1 -1 -1 -1 -1 1 0.27 0.27 0.27 2.135 1 -1 1 1 -1 -1 1 0.27 0.27 0.27 5.856 1 -1 1 -1 -1 1 -1 0.27 0.27 0.27 0.17 7 1 -1 -1 1 1 -1 -1 0.27 0.27 0.27 0.808 1 -1 -1 -1 1 1 1 0.27 0.27 0.27 0.569 1 1.215 0 0 0 0 0 0.746 -0.73 -0.73 1.60 10 1 -1.215 0 0 0 0 0 0.746 -0.73 -0.73 0.56 11 1 0 1.215 0 0 0 0 -0.73 0.746 -0.73 5.54 12 1 0 -1.215 0 0 0 0 -0.73 0.746 -0.73 3.89 13 1 0 0 1.215 0 0 0 -0.73 -0.73 0.746 3.57 14 1 0 0 -1.215 0 0 0 -0.73 -0.73 0.746 2.52 151 0 0 0 0 0 0 -0.73 -0.73 -0.73 5.80∑=2j j x a15 10.9525 10.9525 10.9525 8 8 84.36074.36074.3607∑2y＝51.8443∑=y x j j β37.37 2.6336 7.2948 9.1858 -6.27-6.175.59-10.2019 0.5286 -4.3721y SS ＝58.7432j j j a B b = 0b0.2405 0.6660 0.8387 -0.7838 -0.7713 0.6988 -2.3395 0.1212-1.0093R SS ＝55.2032j j j a B Q 2=0.6333 4.8586 7.7040 4.9141 4.7586 3.9060 23.8676 0.0641 4.4422r SS ＝3.5401231213222231234.90910.24050.66600.83870.78380.77130.6988 2.33950.1212 1.0093y x x x x x x x x x x x x =+++--+-+-()2011137.3710.9525 2.33950.1212 1.0093 4.90911515maj jj j b y x b N N ==-•=--+-=∑∑∑回归关系的显著性测验。
变异来源平方和(SS)自由度(df)均方(MS)F显著程度x10.6332710.63327＜1nsx2 4.858561 4.85856 6.8624*0.05(6.61) x37.7040017.7040010.8814*0.05(6.61) x1x2 4.914101 4.9141010.3994*0.05(6.61) x1x3 4.758611 4.75861 6.9409*0.05(6.61) x2x3 3.906011 3.90601 5.51700.10(4.06) x1223.86763123.8676333.7116**0.01(16.30) x220.0640710.06407＜1nsx32 4.442201 4.44220 6.27430.10(4.06)回归55.203209 6.133698.6635*0.05(4.77)剩余 3.5399850.70799总变异58.7431714方差分析表明，总回归达到显著水平，说明本食品的加香试验与所选因素之间存在显著的回归关系，试验设计方案是正确的，选用二次正交回归组合设计也是恰当的。
除 x1 和 x22 以外，其余各项因子基本达到显著或极显著，说明香料用量、着香时间、着香温度与这一食品的加香有显著或极显著关系。
本试验设计的因素、水平选择是成功的。
在这种回归正交试验中，第一次方差分析往往因为误差（剩余）自由度偏小而影响了检验的精确度。
并且由于回归正交试验计划具有的正交性，保证了试验因素的列与列之间没有互作（即没有相关性）存在，因此我们可以将未达到0.25以上显著水平的因素（或者互作）剔除，将其平方和和自由度并入误差（剩余）项，进行第二次方差分析，以提高检验的精确度。
第二次方差分析结果见下表：变异来源平方和(SS)自由度(df)均方(MS)F显著程度x2 4.858561 4.858568.0263*0.05（5.59）x37.7040017.7040012.7269**0.01（12.20）x1x2 4.914101 4.914108.1180*0.05x 1x 3 4.75861 1 4.75861 7.8612*0.05（5.59） x 2x 3 3.90601 1 3.90601 6.4527*0.05（5.59） x 12 23.86763 1 23.86763 39.4290**0.01（12.20）x 32 4.44220 1 4.44220 7.3385*0.05（5.59） 回归 54.24265 7 7.74895 12.8012**0.01（6.99）剩余 4.23732 7 0.60533总变异58.47997 14第二次方差分析表明，总回归及各项因素均达到显著或极显著水平，说明这一食品加香与试验因素之间存在极显著的回归关系，其优化的回归方程为：本试验由于 m0＝1，故不能进行失拟检验，这是试验的一个缺陷。
