4因素二次回归正交旋转组合设计

结合专业领域知识，将元二次回归正交 组合设计应用于实际问题中，不断积累 实践经验和提升解决问题的能力。
深入了解试验设计原理和方法，如析因 设计、裂区设计、重复测量设计等，以 提高试验设计的效率和准确性。
感谢观看
THANKS
试验方案设计与优化
设计试验方案
根据正交表和因子水平，设计试验方案，包括试验条件、试验步骤和试验数据处理方法等 。
优化试验方案
通过比较不同试验方案的优劣，选择最优方案进行实施。同时，可以根据实际情况对试验 方案进行调整和优化，以提高试验效率和准确性。
注意事项
在进行正交组合设计时，需要注意选择合适的正交表、确定因子水平和编码方式、设计合 理的试验方案，并进行充分的试验前准备和数据处理工作，以确保试验结果的准确性和可 靠性。
率。
预测性
能够建立数学模型，对未知区 域进行预测，为优化提供方向
。
灵活性
可以处理多个因素，每个因素 可以取多个水平，适用于复杂
系统。
直观性
通过图形展示，可以直观地看 出各因素对响应的影响趋势。
缺点分析
模型假设
处理非线性关系的能力有限
元二次回归模型假设响应与因素之间的关 系是二次的，如果实际关系偏离这一假设 ，模型预测可能不准确。
对于高度非线性的系统，元二次回归模型 可能无法提供准确的预测。
对异常值敏感
计算复杂性
如果数据中存在异常值，可能会对模型的 拟合和预测产生较大影响。
对于大量数据和复杂模型，计算可能会变 得复杂和耗时。
适用范围及注意事项
适用范围：适用于需要通过试验来优化响应，且因素水 平不太多、试验成本较高的场合。特别适用于那些对模 型精度要求不高，但需要快速得到优化方向的场合。 1. 在使用元二次回归正交组合设计时，应确保试验数据 满足模型的假设条件。

二次回归正交旋转组合设计优化大肥蘑菇液体培养基杨琴;张桂香;杨建杰;王英利【摘要】为优化大肥蘑菇液体培养基,通过单因子试验确定大肥蘑菇最佳碳源(葡萄糖)、最佳氮源(蛋白胨)及矿物质的适宜浓度(用量)范围,采用二次回归旋转组合设计研究3个参数对大肥蘑菇菌丝生物量的影响,建立数学模型,以获得适宜的配方组合.结果表明,葡萄糖浓度、蛋白胨浓度对大肥蘑菇菌丝体生物量的影响达极显著水平,矿物质添加剂用量达显著水平.最优培养基参数为葡萄糖浓度33.26 g/L、蛋白胨浓度4.24 g/L、矿物质添加剂1.82 mL/L,在该参数组合下,28℃振荡培养8 d,菌丝干重可达16.44 g/L,且经反复试验验证可行.【期刊名称】《甘肃农业科技》【年(卷),期】2017(000)011【总页数】6页(P12-17)【关键词】大肥蘑菇;培养基;二次回归旋转组合;优化【作者】杨琴;张桂香;杨建杰;王英利【作者单位】甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070【正文语种】中文【中图分类】S646.9博斯腾湖位于巴音郭楞蒙古自治州焉耆盆地的博湖县境内，总面积1 228 km2，蓄水量8.0×109m3，是开都河的归宿，孔雀河的源头，更是一座天然的大型调节水库，也是新疆最大的内陆淡水湖。

大肥蘑菇（经ITS序列分析确定［1］）是在新疆博斯腾湖特殊环境条件下形成的极为珍贵的野生食用菌，在分类上隶属于担子菌纲（Basidiomycetes）伞菌目（Agaricales）蘑菇科（Agaricaceae）蘑菇属（Agaricua），其子实体硕大、菌肉肥厚细嫩，通过营养成分、氨基酸组成、矿物质、脂肪酸营养成分的测定［2-3］，发现大肥蘑菇具有极高的风味物质、营养价值和保健作用。

汤建平
( 中国农 业科学院饲 料研究所 ， 家禽 营养与饲料 研究室， 北京 10008 1)
要: 本试验以低胆碱 � 低蛋氨酸饲粮为基础饲粮， 通过两因子二次回归正交旋转组合设计， 对 21 42 日龄肉仔鸡胆碱和蛋氨酸需要量进行研究� 试验选用 21 日龄爱拔益加( A A ) 肉仔鸡 摘 48 0 只 ， 9 12 组为 中心组 ， 随机分为 12 个组 ， 其中 1 8 组为试验组 ， 每组 4 个重复 ， 每个重复 10 只鸡， 公母各占 1/ 2� 分别以胆碱和蛋 氨酸为自变量， 以反映 肉仔鸡生长性能 和屠宰性能的 各项指标为因变量 拟合回 归方 程， 估计 21 42 日 龄肉 仔鸡 胆碱和 蛋氨 酸的 需要 量� 试验期 21 d� 结果表明 : 胆碱和蛋氨酸水平对 21 42 日龄肉仔鸡的平均日采食量 � 料重比 � 腹脂率和肝 kg 时 ， 脂率有显著影响( P < 0.05) � 当胆碱水平在 8 60 1 120 m g / 肉仔鸡平均日采食量随着蛋 氨酸水平的增加而升高， 蛋氨酸水平增至 0.40% 后， 继续增 加对平均日采食量的改善作用不明 0.42% ， kg 时 ， 显 ; 蛋氨酸水平在 0.35% 胆碱水平在 8 6 0 1 120 m g / 肉仔鸡的料重比达到最 0.47 % 时 ， 低值 ; 蛋氨酸水平在 0.30% 随着胆碱水平的增加肉仔鸡腹脂率呈下降趋势 ; 当蛋氨 酸水平在0.30% 0.40% ， 胆碱水平在 1 000 1 400 m g / kg 时， 肉仔鸡肝脂率随着胆碱水平的 增加和蛋氨酸水平的降低呈下降趋势 � � 在本试验条件下， 当 胆碱水平为 99 0 1 030 m g / kg ， 蛋 0.40% � 0. 43% ， ; 1 7 8 0 氨酸 水 平 为 时 肉 仔 鸡 可 达到 最 佳 生 长性 能 当胆 碱 水 平 为 1 8 8 0 mg / kg ， 蛋氨酸水平为 0.37 % 中图分类号 : S8 31 0.38 % 时 ， 肉仔鸡可达到最佳屠宰性能 � 关键词: 胆碱 ; 蛋氨酸 ; 肉仔鸡; 二次回归正交旋转组合设计 ; 响应面 文献标识码 : A 文章编号 : 1006 267 X ( 2012) 06 1019 11 数都是围绕胆碱与其他营养物质的 相互关系进行 的

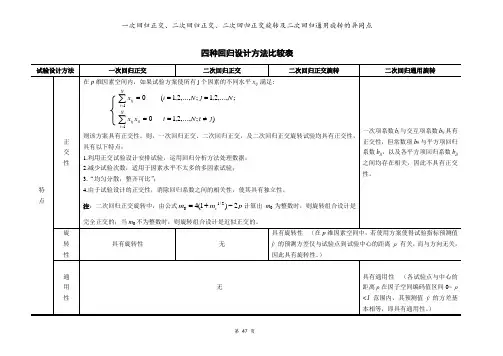
四种回归设计方法比较表试验设计方法一次回归正交二次回归正交二次回归正交旋转二次回归通用旋转特点正交性在p维因素空间内，如果试验方案使所有j个因素的不同水平x ij 满足:);,...,2,1;,...,2,1;,...,2,1(11jtNtxxNjNixNiitijNiij≠=====∑∑==则该方案具有正交性。

则，一次回归正交、二次回归正交，及二次回归正交旋转试验均具有正交性，具有以下特点：1.利用正交试验设计安排试验，运用回归分析方法处理数据；2.减少试验次数，适用于因素水平不太多的多因素试验；3.“均匀分散，整齐可比”；4.由于试验设计的正交性，消除回归系数之间的相关性，使其具有独立性。

注：二次回归正交旋转中，由公式pmmc2)1(42/1-+=计算出m0为整数时，则旋转组合设计是完全正交的；当m0不为整数时，则旋转组合设计是近似正交的。

一次项系数b j与交互项系数b ij具有正交性，但常数项b0与平方项回归系数b jj，以及各平方项回归系数b jj之间均存在相关，因此不具有正交性。

旋转性具有旋转性无具有旋转性（在p维因素空间中，若使用方案使得试验指标预测值ŷ的预测方差仅与试验点到试验中心的距离ρ有关，而与方向无关，因此具有旋转性。

）通用性无具有通用性（各试验点与中心的距离ρ在因子空间编码值区间0< ρ<1范围内，其预测值ŷ的方差基本相等，即具有通用性。

）优点科学地安排实验，用最少的试验次数，获得最全面的试验信息，并对试验结果进行科学分析，从而得到最佳实验条件，迅速建立经验公式，简化计算。

1.中心点试验次数m0有所减少。

2.试验方案具有通用性与旋转性。

消除回归系数之间的相关性，使其具有独立性，剔除回归方程某一变量时，其余变量的回归系数不变。

1.可直接比较各点预测值的好坏，找出预测值相对较优的区域；2.有助于寻找最优生产的过程中排除误差的干扰。

缺点1.只适用于因素水平不太多的多因素试验，且水平数一般不大于3；2.适用性具有局限，一次回归方程经检验可能在区域内部拟合不好。

五,k>2 实现旋转设计借助于组合设计思想
1.中心组合思想
(1)m c 个点布置在半径 R c = k的球面上 (2 )2k个点布置在半径 R = r的球面上,通常位于 (3)m 0 个点布置在因子区域的 中心
n = m c + 2k + m 0 坐标轴上,称 r为星号臂
2. k = 2 D = 1 1 1 1 r r 0 0 0 0 1 1 1 1 0 0 r r 0 0
§6 二次回归的旋转设计
一,问题
y = β 0 + ∑ βi x i + ∑ βij x i x j + ∑ β ii x i2 + ε
i i< j i
要寻找旋转设计 D, X′X满足旋转性条件 0 第 (0,)元素为 n x 2 = λ 2 n i = 1, , k ∑ ji j ∑ x 4 = 3∑ x 2 1 x 2 2 = 3λ 4 n i1 ≠ i 2 ji ji ji j j k λ4 ≠ 2 λ2 k + 2
∑x
j j
ji
= ∑ x ji1 x ji 2 = ∑ x x ji 2 = 0
2 ji1 j j
x 2 = 4 + 2r 2 ∑ ji x21x2 2 = 4 ∑ ji ji
j
x 4 = 4 + 2r 4 ∑ ji
j
为满足旋转性条件
∑x
j
4 ji
= 3∑ x x
2 ji1 j
2 ji 2
∴ 4 + 2 r 4 = 12 r =
2
3.k ≥ 3
∑x
j j
ji
= ∑ x ji1 x ji 2 = ∑ x 2 1 x ji 2 = 0 ji

成分 ， 势必成 本过 高 ， 得对 紫芝深 层次 开发 受到 限 使 制 。利 用液 体深层发 酵技 术可 以在 较短 时 间内获 得
大量菌 丝体及 其发 酵 产 物 ， 以为 大 通 量 开 发 紫芝 可 相 关产 品提供 可 能 。 目前 ， 于 紫 芝 栽 培 和液 体 关 发 酵条件 的研 究 报 道 较 少 ， 无 利 用 五 因素 “ 次 更 二
得其 子实体 ， 但人 工栽 培紫芝 具有 周期 长 ， 成本高 的
缺点 。如果 从子 实体 中提取具 有疗 效 和保健 功能 的
芝科 （ ａ ｏｅｍａ ｃａ ） 灵 芝属 （ ａ ｏ ｅｎ ） 的 Ｇ ｎ ｄ ｒ ｔ ｅｅ ， ａ Ｏ ｎ ｄｒ ａ 中 ｌ 真菌 … 。 自古 以来 被视 为 滋 补 强壮 、 固本 扶正 的珍
西
南
农
业
学
报
２ ３卷
回归 系数之 间相关 性等特 点 ； 二 ， 第 有助 于克服 回归 正 交 设 计 中二 次 回归 预 测 值 ｌ的方 差依 赖 于试 验 ， 点 在 因子空 间 中的位 置 缺点 ， 能有效 地 克Ｊ － 次 即 Ｊ ￣
后 分别在 ２ 、５ ２ 、９ ３ ３ ２ 、７ ２ 、 ｌ℃ 下 ， 每组 ３个 重 复 ， 摇 床培养 。 １３ ５ 依据 单 因素试 验 的结果 确 定 因素 水 平 范 围 ．． 选 取 装 液 量 （ ５ Ｌ 三 角 瓶 ）（ 、 始 ｐ ２０ ｍ Ｘ ）初 Ｈ
１ ３ ６ 不 同接 种 菌龄 对发 酵 的 影 响 分别 向培 养 ．． 液 中接 人菌龄 为 ４ ５ ６ ７ ８ ９ ｄ的种 子 ， 组 ３个 、 、 、 、 、 每
１ 材 料 与 方 法
１ １ 材料 ．

2 i 2 j
x
i，j =1，2„P；
待定参数
以上为 P 元二次回归旋转设计的旋转性条件。
此外，为了使旋转设计成为可能，还必须使信
息矩阵 A 不退化，为此，必须有不等式：
4 p 2 2 P 2
上式为 P 元二次回归的非退化条件。 已证明，只要使 N 个试验点不在同一个球面上， 就能满足非退化条件。或者说只要使 N 个试验点至少 分布于两个半径不等的球面上，就有可能获得旋转设
P 2 2 ˆ D y P 2 4 PN
4 1 2 P 1 4 P 1 4 1 2 2 4 P 2 4 4
（4.11） 由式（4.11）经研究表明，只有采用恰当的方法 确定 4 ，才能满足通用性的要求。如何确定 4 ？对 4 有什么要求呢？总的来说，它必须使上式中 i处的
ˆ 的 二次旋转组合设计具有同一球面预测值 y
方差相等的优点，但回归统计数的计算较繁琐，
若使它获得正交性就能简化计算手续。
在二次旋转组合计划中，一次项和交互项的 回归系数 bj ，bij 仍保持正交，但 b0 与 bjj 之间，
以及 bii 与 bjj 之间都存在相关，即不具正交性，
它们之间的相关矩分别为：
计方案。
为了获得 P 元二次旋转设计方案，就要求既要
满足非退化条件式，又要满足旋转性条件式。
如何才能满足这两方面的条件呢？这主要借助
于组合设计来实现，因为组合设计中 N 个试验点：
N mc m m0
分布在三个半径不相等的球面上：
mc 个点分布在半径为 P 的球面上； c m 个点分布在半径为 的球面上； m0 个点分布在半径为 0 0 的球面上；

第四节二次回归正交设计在应用一次回归正交设计时，如果经过假设检验，发现一次回归方程不合适，就需要用二次或更高次回归方程描述。

通常情况下，使用二次回归一般即可满足要求。

一、二次回归正交试验的组合设计方法二次回归设计就是采用二次多项式作为回归方程。

当变量数为P 时，二次回归模型的一般形式为(3-3-18) 在二次回归模型中，共有q个待估计参数因此，要建立有p个变量的二次回归方程，试验次数应大于q。

而且为了估计未知参数,每个变量所取得的水平不应小于3。

在三水平上做p个变量的全因素试验，试验次数为3p。

当p=4时，三水平的全因素试验次数数量是81次，比p=4时的二次回归系数要多4倍以上，以致剩余度过大。

为了有效地减少不必要的试验次数，提出一种组合设计法。

这种方法是在因素空间中选择几类具有不同特点的点，把它们适当组合成为一个试验计划，此计划应尽量减少试验次数，并且有正交性。

以p=2为例，在有两个变量x1,x2场合下，组合设计由以下9个试验点组成（见表3-3-13）：表3-3-13这9个试验点在平面图上的位置如图3-3-2所示。

图3-3-2当p=3，即有三个变量时，组合设计由15个试验点组成，见表2-14。

这15个试验点在空间的位置，如图3-3-3所示。

表3-3-14一般地，p个变量的组合设计由下列三类试验点组成：第一类点为二水平（-1和1）全因素试验的试验点，这类试验点共有2p个，如果采用1/2或1/4 实施法，则为2p-1或2p-2个试验点。

第二类点为分布在p个坐标轴上的星号点，这类试验点共有2p个，它们与中心点的距离为，称为星号臂。

是待定系数，可根据不同的要求确定值。

第三类试验点为中心点，即各变量都取零水平的试验点。

在中心点上的试验可以只做一次，也可以重复做若干次。

若以N0表示第一类试验点个数，以m0表示第三类试验点个数，则p个变量的组合设计试验点数N为：N=N0+2p+m0用组合设计安排的试验计划有一系列优点：首先，它的试验点比三水平的全因素试验少得多，但仍保持足够的剩余度。

.
一次回归正交设计
某产品的产量与时间、温度、压力和溶液浓度有关。实际生产中，时间控制 在 30~40min，温度控制在 50~600C，压力控制在 2*105~6*105Pa，溶液浓度控制 在 20%~40%，考察 Z1~Z2 的一级交互作用。
因素编码
Zj(xj)
Z1/min
Z2/oC
Z3/*105Pa
Z4/%
下水平 Z（1j -1）
30
50
2
20
上水平 Z2j
40
60
6
40
（+1）
零水平 Z0j（0）
35
55
4
30
变化间距
5
5
2
10
编码公式 X1=（Z1-35） X2=(Z2-55）/5 X3=(Z3-4)/2 X4=(Z4-30)/10
/5
选择 L8（27)正交表
因素 x1,x1,x3,x4 依次安排在第 1、2、4、7 列，交互项安排在第 3 列。
试验号 X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2
Yi
1
1
1
1
1
1
1
9.7
2
1
1
1
-1
-1
1
4.6
3
1
1
-1
1
-1
-1
10.0
.
.
4
1
1
-1
-1
1
-1
11.0
5
1
-1
1
1
-1
-1
9.0
6
1
-1
1
-1
1

水平 ，ห้องสมุดไป่ตู้明试验数据与所采用 的二 次数学模型基本 上是符合 说
的 ， 程 与 实 际 情 况 拟 合得 较 好 ， 以直 接 利 用 模 型进 行 试 验 方 可
因素与产量的效应分析 和模 拟寻优 ， 提出该 品种 高产 配套栽
１ ２
试 验因素
一
２
一ｌ
Ｏ
培 技 术 的 各项 主要 农 艺 措 施 。
利 用 Ｄ Ｓ和 Ｅ ｃｌ 行试 验数 据 的 统 计 分 析 。 Ｐ ｘｅ 进
２ 结 果 与 分 析
２ １ 产 量 方 程 的 建 立 ．
区试和生产试验 中产量均 居第 ｌ位 ， 在贵州 中西部具有 良好
的丰 产 性 、 产 性 和 适 应 性 … 。本 试 验 结 合 科 技 部 农 业 科 技 稳 成 果 转 化 项 目 ， 贵 州 中 部 地 区对 提 高 贵 单 ８号 产 量 的模 式 在
密度 （ ， ｈ ）ｌ ０ ２ ０ ３ ０ ５ ０ ６ ０ ７ ０ 株／ ｍ。 ２０ ０ ７０ ０ ９０ ０ １ ０ ３０ ０ ５０ ０ ０
Ｎ（ ，ｇ ｈ ｋ／ｍ ） １０ ２ ０ ０
０
１０ ２ ６ ０
２０ ４ １０ ２
３０ ６ １０ ８
４０ ８ ２０ ４
一
１２ 一 １
江苏 农 业 科 学
２１ 第 １ ００年 期
宋 碧， 柏光晓， 袁玉清 ， 等．贵单 ８号玉米高产配套栽培技 术研 究［］ Ｊ ．江苏农业科学，０ ０ １ ：１ ２ １ （ ） １２—１４ １
贵单 ８ 号玉米高产配套栽培技术研究
宋 碧 ， 光晓 ，袁 玉清 ，卢 敏 ，罗文周 柏
西南山区玉米带是我 国的第三 大玉米带 ， 贵州 中西部地

9回归旋转试验设计本章要点：主要介绍了回归旋转设计的基本原理、实现条件、组合设计的步骤和统计分析方法，并给出二次回归正交旋转试验设计的计算案例。

重点：回归正交旋转设计的实现条件、组合设计的方法、方程的建立及显著性检验。

难点：回归正交旋转设计正交和旋转的实现条件及其统计分析。

9.1回归旋转试验设计的基本原理前面所介绍的“回归正交设计”，具有试验处理数比较少，计算简便、消除回归系数之间的相关性等优点。

但它也存在一定的缺点，即二次回归预测值的方差随试验点在因子空间的位置不同而呈现较大的差异。

由于误差的干扰，就不易根据预测值寻找最优区域。

为了克服这个缺点，人们通过进一步研究，提出了回归旋转设计（whirly design ）。

所谓旋转性是指试验因素空间中与试验中心距离相等的球面上各处理组合的预测值的方差具有几乎相等的特性，具有这种性质的回归设计称回归旋转设计。

这种设计的意 义在于可以直接比较各处理组合预测值的好坏，从而找出预测值相对优良的区域。

9.1.1回归设计旋转性条件旋转设计包括一次、二次和三次旋转设计，但研究中最常见的设计是二次回归旋转设计。

下面以三元二次回归方程来讨论回归正交的旋转性问题。

二次正交多项式方程的估计值为： 如果以三因素二次回归正交设计的数学模型为例：因此其信息矩阵A 为：T A=x x=ˆy ˆy332011ˆj j ij i j jj jj i jj y b b x b x x b x ===+++∑∑∑2220112233121213132323111222333ˆy b b x b x b x b x x b x x b x x b x b x b x =+++++++++1231213231231121312131231121322222232a a a a a a a a a a a aa a a a a a a a a a a a a a a a a n x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑223121232312223312313231322222322222a a a a a a a a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑∑∑∑∑ 对233121231231212123232222332a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x∑∑∑∑∑∑∑∑∑称13123131231323123232322232322233a a a a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑ 1121342222a a a a a x x x x x ∑∑∑ 部223422a a a x x x ∑∑ 分34a x ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎝⎭∑上述信息矩阵中的各个元素可用一般形式表达为： ，其中x 的指数1Q 、2Q 、3Q 分别可取0、1、2、3、4等非负整数。

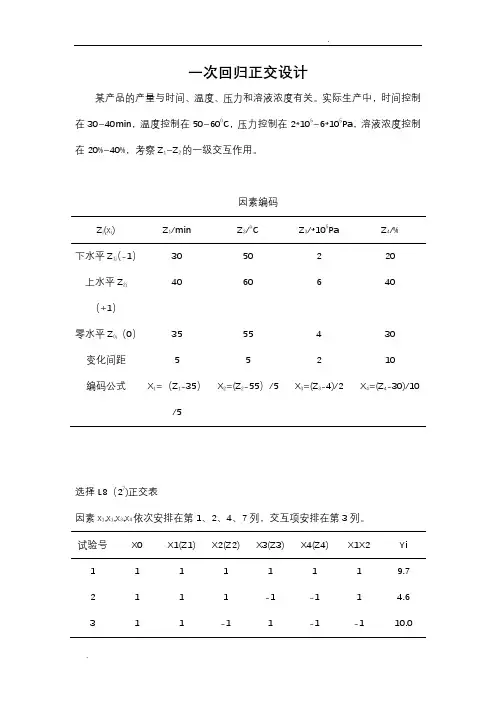
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。

实际生产中，时间控制在30~40min，温度控制在50~600C，压力控制在2*105~6*105Pa，溶液浓度控制在20%~40%，考察Z1~Z2的一级交互作用。

因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j（-1）30 50 2 20上水平Z2j（+1）40 60 6 40零水平Z0j（0）35 55 4 30变化间距 5 5 2 10编码公式X1=（Z1-35）/5 X2=(Z2-55）/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8（27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列，交互项安排在第3列。

试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。

Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验：1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。

环模秸秆压块机秸秆压缩力试验研究陈树人;沈柳柳【摘要】试验采用四因素五水平二次回归正交旋转中心组合设计法，以水稻秸秆和稻壳为原料，主轴转速、含水率、稻壳含量和秸秆长度为试验影响因子，秸秆压缩力为试验指标，利用9JYK－2000A型环模秸秆压块机进行秸秆压缩力试验研究。

结果表明：当主轴转速为170 r／min、含水率为20％、稻壳含量为30％、秸秆长度为15 mm时，秸秆压缩力有最佳值为20．407kN；各因素对环模秸秆压块机秸秆压缩力贡献率主次顺序依次为：含水率＞秸秆长度＞稻壳含量＞主轴转速。

试验验证可知：该组合下试验值与试验模型预测值之间相对误差平均值为1．94％，可以为环模秸秆压块机压缩机理研究和分析提供必要的参数依据。

%Experiment is designed as quadratic regression orthogonal of four factors and five levels , which takes spindle speed, moisture content, rice husk content and straw length as influence factors ,and straw compression force as test in-dex .Compression force tests were performed by taking a 9 JYK-200 A circular mold briquetting machine as testing appa-ratus withrice straw and rice husk as raw material .The result indicated that when the raw material had moisture content of 20%,rice husk content of 30%,straw length of 15mm and spindle speed of 170r/min,the straw compression force had the optimal value of 20.407KN.The order of contribution rate of every experiment factor on target index was obtained as follows:moisture content, straw length,rice husk content,spindle speed.The verification ofthe experiment shows that the relative error between the predictive valuesand experimental values is 1.94%,which can provide the necessary parame-ters for the research and the analysis of circular mold briquetting machine .【期刊名称】《农机化研究》【年(卷),期】2016(000)010【总页数】6页(P169-173,182)【关键词】压块机;水稻秸秆;压缩力;优化;因素分析【作者】陈树人;沈柳柳【作者单位】江苏大学现代农业装备与技术教育部重点实验室，江苏镇江212013;江苏大学现代农业装备与技术教育部重点实验室，江苏镇江 212013【正文语种】中文【中图分类】S817.11+5我国作为农业大国，秸秆资源丰富，分布广泛[1-2]。

二次回归正交组合设计及其统计分析一、组合设计（一）组合设计的概念组合设计：在自变量（因素，也称因子）空间中选择几种类型的点，组合成的试验计划。

（P.31）由于组合设计可选择多种类型的点，而且有些类型的点的数目（试验处理数）又可适当调节，因此组合设计在调节试验处理数N（从而在调节剩余自由度）方面，要比全面试验灵活得多。

（二）组合设计的组成二次回归正交组合设计试验方案由三种类型的点组成，即：式中：N为处理组合数；为二水平析因点，（p为因素个数）；为轴点，；为中心区（或原点）。

①二水平析因点（）：这些点的每一个坐标（自变量）都各自分别只取1或-1；这些试验点的数目记为。

当这些点组成二水平全面试验时，。

而若这些点是根据正交表配制的二水平部分实施（1/2或1/4等）的试验点时，。

调节了这个，就相应地调节了剩余自由度。

②轴点（）：这些点都在坐标轴上，且与坐标原点（中心点）的距离都为。

也就是说，这些点只有一个坐标（自变量）取或，而其余坐标都取零。

这些点在坐标图上通常用星号标出，故又称星号点。

其中称为轴臂或星号臂，是待定参数，可根据下述正交性或旋转性要求而确定。

这些点的数目显然为2P，记为。

③原点（）：又称中心点，即各自变量都取零水平的点，该试验点可作1次，也可重复多次，其次数记为。

调节，显然也能相应地调节剩余自由度。

（三）试验点（处理）的分布情况1、P=2（二因素）的分布情况（1）处理组合数：若=1，处理组合数为9，即（2）处理组合表2.2.1。

（P.32）（3）处理组合分布图2.2.1。

（P.31）二因素（X1、X2）二次回归组合设计的结构矩阵如表2.2.2。

（P.32）2、P=3（三因素）的分布情况（1）处理组合数：若=1，处理组合数为15，即（2）处理组合表：P=3（X1、X2、X3）二次回归正交组合设计，由15个试验点组成。

如表2.2.3所示。

（P.33）（3）处理组合分布图2.2.2。

（P.32）三因素（X1、X2、X3）二次回归组合设计的结构矩阵如表2.2.4。