一次回归正交设计计算
- 格式:xls
- 大小:27.50 KB
- 文档页数:2



回归正交试验设计一、概述(1)回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式,用于描述自变量与因变量之间的函数关系。
它的主要缺点是毫不关心试验数据如何取得,这样,不仅盲目地增加了试验次数,而且试验数据还往往不能提供充分的信息。
因此,有些工作者将经典的回归分析方法描述成:“这是撒大网,捉小鱼,有时还捉不到鱼”。
所以说,回归分析只是被动地处理试验数据,并且回归系数之间存在相关关系,若从回归方程中剔除某个不显著因素时,需重新计算回归系数,耗费大量的时间。
正交试验设计的主要优点是科学地安排试验过程,用最少的试验次数获得最全面的试验信息,并对试验结果进行科学分析(如方差分析),从而得到最佳试验条件,但是它的主要缺点是试验结果无法用一个经验公式来表达,从而不便于考察试验条件改变后,试验指标将作如何变化。
(2)回归正交试验设计回归正交试验设计,实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法,它利用正交试验设计法的“正交性”特点,有计划、有目的、科学合理地在正交表上安排试验,并将试验结果用一个明确的函数表达式即回归方程来表示,从而达到既减少试验次数、又能迅速地建立经验公式的目的。
根据回归模型的次数,回归正交试验设计又分为一次回归试验设计和二次回归试验设计。
二、一次回归正交试验设计(一)一次回归正交试验设计的概念一次回归设计研究的是一个因素z (或多个因素z 1,z 2,……)与试验指标y 之间的线性关系。
当只研究一个因素时,其线性回归模型:y =β0+β1z +e (1)其回归方程为:z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数,e 是随机误差,是一组相互独立、且服从正态分布N(0,σ2)的随机变量。
可以证明,∧0β、∧1β和∧y 是β0、β1和y 的无偏估计,即E(∧0β)=β0,E(∧1β)=β1,E(∧y )=y一次回归正交试验设计是通过编码公式x =f(z) −− 即变量变换,将式(2)变为:x b b y 10+=∧(3)且使试验方案具有正交性,即使得编码因素X的各水平之和为零:∑==mi ix1(4)式中m 是因素x 的水平数。

正交回归(正交多项式回归)多项式回归虽然是一种有效的统计方法,但这种方法存在着两个缺点:一是计算量较大,特别是当自变量个数较多,或者自变量幂较高时,计算量迅速增加;二是回归系数间存在着相关性,从而剔除一个变量后还必须重新计算求出回归系数。
当自变量x的取值是等间隔时,我们可以利用正交性原理有效地克服上述缺点。
这种多项式回归方法就是本节将要介绍的正交多项式回归。
一、正交多项式回归的数学模型设变量y和x的n组观测数据服从以下k次多项式(2-4-17)令(2-4-18)…分别是x的一次、二次,…k次多项式,a ij是一些适当选择的常数,如何选择将在下面讨论(i=1,2,…,n)。
将(2-4-18)式代入(2-4-17)式,则有(2-4-19)比较(2-4-19)和(2-4-17)式可知,二者系数间存在简单的函数关系,只要求出,就可以求出。
若把…看作新的自变量,则(2-4-19)式就成为一个k元线性模型,其结构矩阵为(2-4-20) 正规方程为(2-4-21)(2-4-22) 其中在上节中我们遇到的困难是解正规方程系数矩阵的工作量太大,如果我们有办法使其对角线上的元素不为零,而其余元素均为零,那么计算就大大简化了,而且同时消去了系数间的相关性。
对于…我们可以通过选择系数a10,a21,a20,…,a k,k-,…,a k0使得i(2-4-23)(2-4-24)则正规方程组为(2-4-29)回归系数为(2-4-30)满足(2-4-23)和(2-4-24)式的多项式组…我们称之为正交多项式。
显然这里关键的问题是如何找出一组正交多项式。
换言之,就是如何选择系数a10,a21,a20,…,a k,k-i,…,a k0使(2-4-23)和(2-4-24)式成立。
在正交多项式回归中自变量的选择是等间隔的,设间隔为h,x0=a, 则(2-4-31)(2-4-32)则(2-4-33)由此可见,是1至n的正整数。
只要我们用代替x作为自变量,问题就变得简单了。

一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式,该设计最基本的特点是每一个自变量只考虑一次。
这种设计方法可以通过排列组合的方式得到各种不同的设计方案,使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。
一次回归正交设计在实验设计中被广泛使用,尤其在化学制药、工业生产等领域得到了广泛运用。
二次回归正交设计是一种基于一次回归正交设计的设计方式,这种设计方式可以进一步增加实验信息的获取。
在二次回归正交设计中,依然按照一次正交设计的方式来设计实验,但是在每个单独的自变量上,提高对其的测量次数,使得对这些自变量的测量更加准确。
同时,在某些需要深入探究的因素上,可以通过将这些因素的实验次数进一步提高,来获取相关信息。
二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。
在二次回归旋转设计中,实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。
这样可以在保证基本信息获取的同时,增加获取高阶信息的可能性。
旋转设计特别适合于需要同时考虑多个变量的实验设计,可以使各个变量之间更加独立,减少不必要的干扰。
总的来说,在实验设计领域中,三种设计方法各自有着各自的优势。
对于需要更精准的信息获取的实验,应该选择更高阶的设计方法,在更基础的实验中则可以选择更为简单的设计方法。
另外,在选择设计方法的过程中,还应该根据实验具体情况灵活选择,使得实验设计更加科学合理。





正交试验结果分析的回归分析方法方法简述本节的题目表明,本方法仅仅是对正交试验结果进行分析的一种方法。
在对正交试验结果进行分析之前,如何明确试验指标、因素和水平,如何选择正交表,如何进行表头设计,如何做实验等,与本章所讲的常规的正交试验设计方法是完全相同的。
本方法实际上是用正交表来设计试验方案,再用逐步回归方法来处理正交试验的实验数据。
用正交表来设计试验方案,目的是使数据点的分布均匀合理;用逐步回归方法来处理实验数据,目的是为了得到有多种用途的数学回归式。
回归模型和回归方法正交试验设计方法特别适合于解决多因素试验问题。
化工上,大多数的实际问题都是多因素的问题,而且多数问题都是非线性的问题。
一个适用于多元线性和非线性回归的回归模型,是下式所示的多元二次多项式:(以4个自变量为例)(4-7)可见,在4个自变量时,若包括b0则待求的回归系数就多达15个。
为此实验的次数至少应16次,而且求回归系数的过程和应用回归式求y的计算过程都很长,舍入误差较大。
实际上,如同在方差分析时有些列在F检验中会不显著一样,在按式(4-7)进行回归分析时有些项在F检验中也会不显著。
若只让F检验显著的项进入和保留在回归式中,则所得的回归式肯定会比式(4-7)简化许多。
为此,我们推荐使用逐步回归方法来进行多元二次多项式的回归。
逐步回归方法见本书的第3章3.5.5。
在这种回归方法中,用每次选入时至多选入一项,每次剔除时至多剔除一项,选入、剔除交替进行的办法来进行回归操作。
该选入时,从当前尚在回归式之外的众“项”中选择F值最大且F检验显著的一项,送入回归式。
该剔除时,从当前已在回归式之中的众“项”中选择F值最小且F检验不显著的一项,从回归式剔除出去。
由此可知,在最后所得的回归式中,每一项回归系数的F检验都是显著的。
上面说到每次选入时至多选入一项,其中的“项”指的是式(4-7)中用“+”隔开的项,如x3, 或x1x2,或等,选择正交表时即使不考虑交互作用x2×x3,进行回归分析最后所得的回归式中也可能含有x2x3一项。
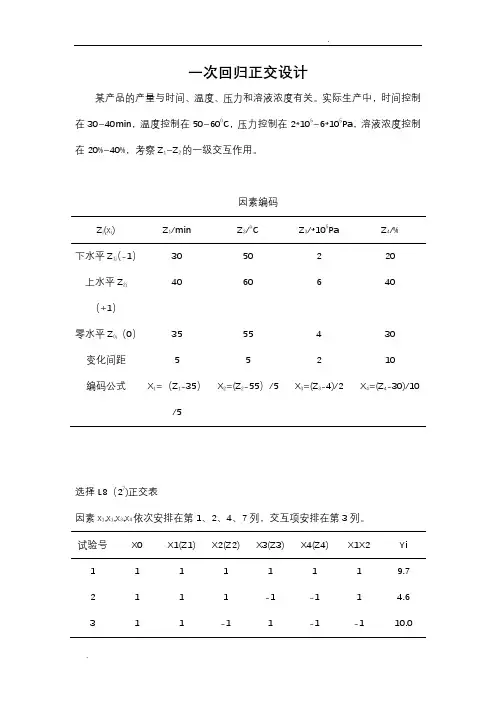
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
正交试验设计方法(1)(2008-12-17 12:59:39)标签:正交设计杂谈分类:其他5. 1试验设计方法概述试验设计是数理统计学的一个重要的分支。
多数数理统计方法主要用于分析已经得到的数据,而试验设计却是用于决定数据收集的方法。
试验设计方法主要讨论如何合理地安排试验以及试验所得的数据如何分析等。
例 5-1 某化工厂想提高某化工产品的质量和产量,对工艺中三个主要因素各按三个水平进行试验(见表 5-1)。
试验的目的是为提高合格产品的产量,寻求最适宜的操作条件。
表 5- 1 因素水平因素温度℃压力 Pa加碱量 kg水平符号T p m1T1(80 )p1(5.0)m 1(2.0)2T(100)p (6.0)m (2.5)2223T3(120)p3(7.0)m3(3.0)对此实例该如何进行试验方案的设计呢?很容易想到的是全面搭配法方案(如图5-1 所示):此方案数据点分布的均匀性极好,因素和水平的搭配十分全面,唯一的缺点是实验次数多达 33= 27 次(指数 3 代表 3 个因素,底数 3 代表每因素有 3 个水平)。
因素、水平数愈多,则实验次数就愈多,例如,做一个 6 因素 3 水平的试验,就需 36=729 次实验,显然难以做到。
因此需要寻找一种合适的试验设计方法。
图 5- 1 全面搭配法方案试验设计方法常用的术语定义如下。
试验指标:指作为试验研究过程的因变量,常为试验结果特征的量(如得率、纯度等)。
例1的试验指标为合格产品的产量。
因素:指作试验研究过程的自变量,常常是造成试验指标按某种规律发生变化的那些原因。
如例 1 的温度、压力、碱的用量。
水平:指试验中因素所处的具体状态或情况,又称为等级。
如例 1 的温度有3 个水平。
温度用 T 表示,下标1、2、 3 表示因素的不同水平,分别记为T1、 T2、 T3。
常用的试验设计方法有:正交试验设计法、均匀试验设计法、单纯形优化法、双水平单纯形优化法、回归正交设计法、序贯试验设计法等。