回归正交试验设计

回归正交试验设计一、概述（1）回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式，用于描述自变量与因变量之间的函数关系。

它的主要缺点是毫不关心试验数据如何取得，这样，不仅盲目地增加了试验次数，而且试验数据还往往不能提供充分的信息。

因此，有些工作者将经典的回归分析方法描述成：“这是撒大网，捉小鱼，有时还捉不到鱼”。

所以说，回归分析只是被动地处理试验数据，并且回归系数之间存在相关关系，若从回归方程中剔除某个不显著因素时，需重新计算回归系数，耗费大量的时间。

正交试验设计的主要优点是科学地安排试验过程，用最少的试验次数获得最全面的试验信息，并对试验结果进行科学分析（如方差分析），从而得到最佳试验条件，但是它的主要缺点是试验结果无法用一个经验公式来表达，从而不便于考察试验条件改变后，试验指标将作如何变化。

（2）回归正交试验设计回归正交试验设计，实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法，它利用正交试验设计法的“正交性”特点，有计划、有目的、科学合理地在正交表上安排试验，并将试验结果用一个明确的函数表达式即回归方程来表示，从而达到既减少试验次数、又能迅速地建立经验公式的目的。

根据回归模型的次数，回归正交试验设计又分为一次回归试验设计和二次回归试验设计。

二、一次回归正交试验设计（一）一次回归正交试验设计的概念一次回归设计研究的是一个因素z （或多个因素z 1，z 2，……）与试验指标y 之间的线性关系。

当只研究一个因素时，其线性回归模型：y ＝β0＋β1z ＋e (1)其回归方程为：z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数，e 是随机误差，是一组相互独立、且服从正态分布Ｎ（０，σ２）的随机变量。

可以证明，∧0β、∧1β和∧y 是β０、β１和y 的无偏估计，即Ｅ（∧0β）＝β０，Ｅ（∧1β）＝β1，Ｅ（∧y ）＝y一次回归正交试验设计是通过编码公式x ＝f(z) −− 即变量变换，将式（２）变为：x b b y 10+=∧(3)且使试验方案具有正交性，即使得编码因素Ｘ的各水平之和为零：∑==mi ix1(4)式中m 是因素x 的水平数。

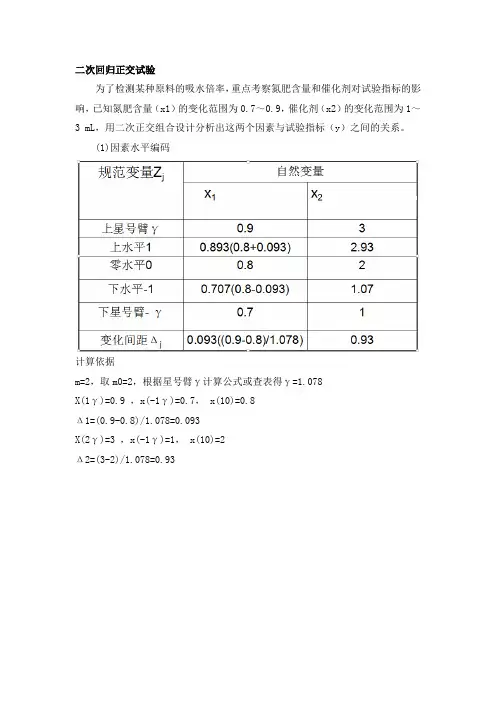
二次回归正交试验为了检测某种原料的吸水倍率，重点考察氮肥含量和催化剂对试验指标的影响，已知氮肥含量（x1）的变化范围为0.7～0.9，催化剂（x2）的变化范围为1～3 mL，用二次正交组合设计分析出这两个因素与试验指标（y）之间的关系。

(1)因素水平编码计算依据m=2，取m0=2，根据星号臂γ计算公式或查表得γ=1.078X(1γ)=0.9 ，x(-1γ)=0.7， x(10)=0.8Δ1=(0.9-0.8)/1.078=0.093X(2γ)=3 ，x(-1γ)=1， x(10)=2Δ2=(3-2)/1.078=0.93(2)试验方案（3）回归方程的建立借助excel分析如下：①回归方程显著性检验：F=186.5564，，，12.4)74(95.0=F因此回归方程非常显著。

'74.41'37.2375.656.2609.952.468y 212121z z z z z z ----+= ②偏回归系数的显著性检验9.496.113305.113806.113308.47058.14583.1822.44615.5528.4705701.274.41)(8.1458701.224.23)(3.182475.6)(2.4461324.656.265.552324.609.95.113801046852206303)(12211122122122222222112111122121212122212222221121122121=-=-==++++=++++==⨯===⨯===⨯===⨯===⨯===-=-=∑∑∑∑∑∑∑=======R T e R ni in i i ni ni i n i in i i n i iT SS SS SS SS SS SS SS SS SS z b SS zb SS z z b SS z b SS z b SS y n y SS 方差分析：dfT=n-1=10-1=9 df1=df2=df12=df1’=df2’=1dfR=df1+df2+df12+df1’+df2’=1+1+1+1+1=5dfe=dfT-dfR=9-5=4MS1=522.5/1=522.5 MS2=SS2/df2=4461.2/1=4461.2 MS12=SS12/df12=182.3MS1’=SS1’/df1’=1458.8MS2’=SS2’/df1’=4705.8MSR=SSR/dfR=11330.6/5=2266.1MSe=SSe/dfe=49.9/4=12.5F1=MS1/MSe=522.5/12.5=41.8F2=MS2/MSe=4461.2/12.5=356.9F12=MS12/MSe=182.3/12.5=14.6F1’=MS1’/MSe=1458.8/12.5=116.7F2’=MS2’/MSe=4705.8/12.5=376.5FR=MSR/MSe=2266.1/12.5=181.3F0.01(1,4)=21.20 F0.05(1,4)=7.71 F0.01(5,4)=15.52 F0.05(5,4)=6.26失拟性检验本例零水平试验次数m0=2，可进行失拟性检验5.45.521220521225)509512(21)259081262144()(12201020101=-=+-+=-=∑∑==m i i m i ie y m y SSSSLf=SSe-SSe1=49.9-4.5=45.4 dfe1=m0-1=2-1=1 dfLf=dfe-dfe1=4-1=359.53)1,3(37.31/5.43/5.45/1/1,01====F df SSe df SS FLf e LfLf检验结果表明，失拟不显著，回归模型与实际情况拟合很好。

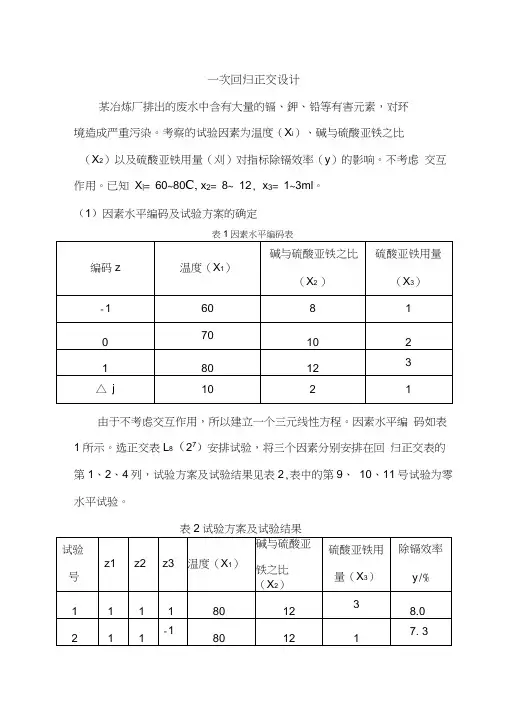
一次回归正交设计某冶炼厂排出的废水中含有大量的镉、鉀、铅等有害元素，对环境造成严重污染。

考察的试验因素为温度（X i）、碱与硫酸亚铁之比（X2）以及硫酸亚铁用量（刈）对指标除镉效率（y）的影响。

不考虑交互作用。

已知X|= 60~80C, x2= 8~ 12, x3= 1~3ml。

（1）因素水平编码及试验方案的确定由于不考虑交互作用，所以建立一个三元线性方程。

因素水平编码如表1所示。

选正交表L8（27）安排试验，将三个因素分别安排在回归正交表的第1、2、4列，试验方案及试验结果见表2,表中的第9、10、11号试验为零水平试验。

表2试验方案及试验结果⑵回归方程的建立表3试验结果及计算表由表3计算a 」皆 \ 二-72.〕6. 6 182n i.i11回归方程为y = 6.6182 0.5125/ 0.5375Z 2 0.3125Z 3由该回归方程偏回归系数绝对值的大小，可以得到各因素的主次 顺序为：X 2>X 1>X 3，即液固比 >乙醇浓度>回流次数。

又由于各偏回归 系数都为正，所以这些影响因素取上水平时，试验指标最好。

(3)回归方程显著性检验b 2b 3、Z 1i Y ii =1m c ' Z 2i%i =1i =1Z 3i Y im c41二 0.5125843二 0.537582^50. 3125 8SS = m c b 2= 8汉 0.5125 = 2.101 = m c b 荻 8 0.53752二 2.311 SQ = m j b ； = 8 0.31252 = 0.781SQ = SS + SS2 + SS3 + SS 2 + SS 厂 2.101+ 2.311+ 0.781= 5.193SS= SS-S&5. 2 9 6- 5. 1 93 0.方差分析结果见表4。

表4方差分析表差异源 SS df MS F 显著性 Z 1 2.101 1 2.101 142.9 ** Z 2 2.311 1 2.311 157.2 ** Z 3 0.781 1 0.781 53.1 ** 回归 5.193 3 1.731117.8**残差 0.103 70.0147总和5.296n — 1 = 10注：F o.o1（1, 7）= 12.25, F o.o1（3, 7） = 8.45可见，三个因素对试验指标都有非常显著的影响， 所建立的回归 方程也非常显著。

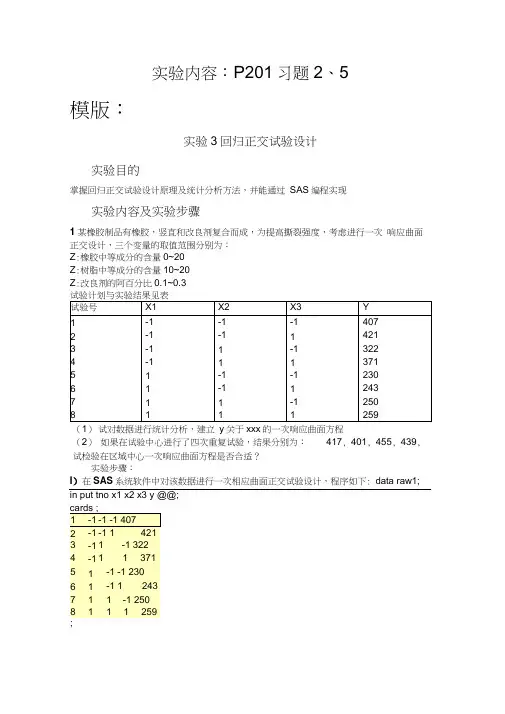
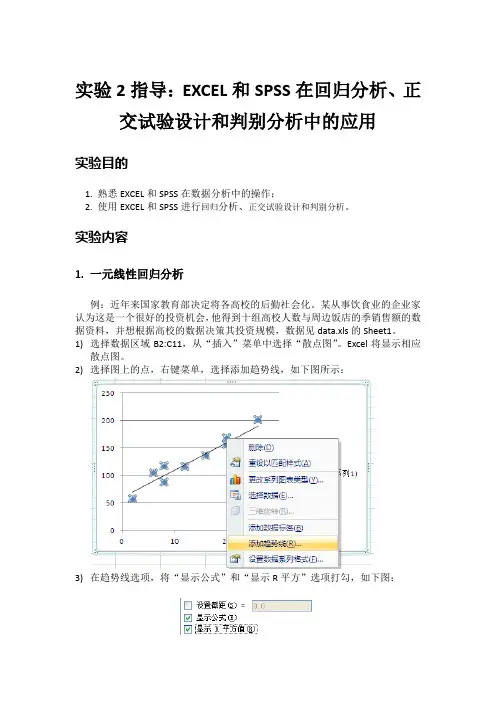
实验内容：P201习题2、5模版：实验3回归正交试验设计实验目的掌握回归正交试验设计原理及统计分析方法，并能通过SAS编程实现实验内容及实验步骤1某橡胶制品有橡胶，竖直和改良剂复合而成，为提高撕裂强度，考虑进行一次响应曲面正交设计，三个变量的取值范围分别为：Z:橡胶中等成分的含量0~20Z:树脂中等成分的含量10~20Z:改良剂的阿百分比0.1~0.3（1）试对数据进行统计分析，建立y关于xxx的一次响应曲面方程（2）如果在试验中心进行了四次重复试验，结果分别为：417, 401, 455, 439, 试检验在区域中心一次响应曲面方程是否合适？实验步骤：I）在SAS系统软件中对该数据进行一次相应曲面正交试验设计，程序如下: data raw1; in put tno x1 x2 x3 y @@;cards ;1-1-1 -1 4072-1-1 1 4213-11 -1 3224-11 1 37151-1 -1 23061-1 1 24371 1 -1 25081 1 1 259;结果1Source DF Sum of SquaresMe«in Square F Value Pr > FModel338443*37500 12B14.4583B 12.2S0.0174Error 44175*50000 1043,87500Corrected Total7 42613*87500R-Square Coeff齒r Root MSE y Mean0.9D2027 10.32651 32,30305 312J75DSource DF Type I SS Mean Square F Value Pr > Fxl13G315J2500 3G316.12500 94.790.0041x211225J2500 1226.12600 1.170.333Sx31903.12510 903.12500 0.070.4049Source DFType HI SS1Mean Square F Veilue Pr > Fxl186816.1260036315,12500 S4.79 0.0041x2 11225.12500 1225.12500 b 17 0.3396x3190S.12GOO 903.12600 0.87 0.4049StandardParameter Est imate Error t Value Pr > IIIIntercept 312.B750000 11.42297575 £7.99 <.00011xl-67J750000 11.42297575 -5.SO 0.0041x2-12.3750000 11.42297575 -1.080.3396x310.6250000 11.42297575 0.93 0.4049由上述结果可得到一次响应曲面方程:y = 312875-67.375% -12.375X2 10.625x3从方差分析结果来看，X2和X3的显著性不高，可推断该曲面方程的忽略了几个变量之间的交互作用，但是拟合度已经达到90.2027%，整个实验还是显著的。

一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式，该设计最基本的特点是每一个自变量只考虑一次。

这种设计方法可以通过排列组合的方式得到各种不同的设计方案，使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。

一次回归正交设计在实验设计中被广泛使用，尤其在化学制药、工业生产等领域得到了广泛运用。

二次回归正交设计是一种基于一次回归正交设计的设计方式，这种设计方式可以进一步增加实验信息的获取。

在二次回归正交设计中，依然按照一次正交设计的方式来设计实验，但是在每个单独的自变量上，提高对其的测量次数，使得对这些自变量的测量更加准确。

同时，在某些需要深入探究的因素上，可以通过将这些因素的实验次数进一步提高，来获取相关信息。

二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。

在二次回归旋转设计中，实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。

这样可以在保证基本信息获取的同时，增加获取高阶信息的可能性。

旋转设计特别适合于需要同时考虑多个变量的实验设计，可以使各个变量之间更加独立，减少不必要的干扰。

总的来说，在实验设计领域中，三种设计方法各自有着各自的优势。

对于需要更精准的信息获取的实验，应该选择更高阶的设计方法，在更基础的实验中则可以选择更为简单的设计方法。

另外，在选择设计方法的过程中，还应该根据实验具体情况灵活选择，使得实验设计更加科学合理。

正交试验设计及分析(多实现途径)引言概述:正交试验设计是一种重要的统计方法，用于确定实验中不同因素对结果的影响。

它可以帮助研究者系统地设计实验，降低实验数量和成本，并提供可靠的分析结果。

本文将介绍正交试验设计的概念、原理，以及多种实现途径，以便读者根据自身需求选择合适的方法进行实验。

正文内容:1.正交试验设计的概念和原理:1.1定义:正交试验设计是一种通过系统地变动因素水平来确定因素对结果的影响的方法。

它将多个因素分解为一些离散的水平，以便在有限实验中进行测试。

1.2原理:正交试验设计基于正交矩阵的原理，该矩阵具有特定的数学性质，可以保证不同因素之间的相互独立性，从而减少实验数量。

2.正交试验设计的多实现途径:2.1Taguchi方法:Taguchi方法是一种常用的正交试验设计方法，它通过选择最优的因素水平组合来优化结果的表现。

它能够在较少的实验次数下找到最佳的因素配置。

2.2BoxBehnken设计:BoxBehnken设计是一种常用的三水平正交试验设计方法，适用于3个或更多个因素的试验。

它通过正交矩阵将因素水平组合成三水平，并通过优化方法确定最佳结果。

2.3中心组合设计:中心组合设计是一种将中心点设置为固定因素水平的正交试验设计方法。

该设计方法可以估计因素对结果的线性和二次的影响，适用于连续和离散因素。

2.4贝叶斯优化设计:贝叶斯优化设计是一种基于贝叶斯统计模型的正交试验设计方法。

它能够在先验知识不完全或验证数据有限的情况下，利用概率推论来确定最佳因素配置。

3.正交试验设计的分析方法:3.1方差分析:方差分析是一种常用的正交试验设计分析方法，用于确定各个因素之间的显著性差异。

它通过计算方差的比值来判断因素对结果的影响程度。

3.2回归分析:回归分析是一种统计方法，用于描述和预测因变量与一个或多个自变量之间的关系。

在正交试验设计中，回归分析可以用来确定因素对结果的线性和非线性影响。

3.3主效应图:主效应图是一种简明直观的分析方法，通过图形展示各个因素对结果的平均水平差异。

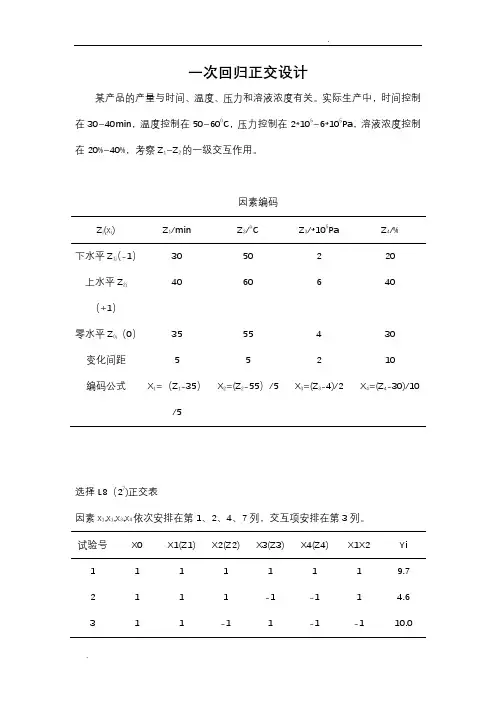
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。

实际生产中，时间控制在30~40min，温度控制在50~600C，压力控制在2*105~6*105Pa，溶液浓度控制在20%~40%，考察Z1~Z2的一级交互作用。

因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j（-1）30 50 2 20上水平Z2j（+1）40 60 6 40零水平Z0j（0）35 55 4 30变化间距 5 5 2 10编码公式X1=（Z1-35）/5 X2=(Z2-55）/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8（27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列，交互项安排在第3列。

试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。

Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验：1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。

三元二次正交回归旋转通用设计创作说明在工程领域，每个设计必须经过多次修正来优化其性能。

而三元二次正交回归旋转通用设计便是一种方法，可有效减少这些周期，提高工程效率。

本文将从三元二次正交、正交回归设计、正交设计旋转、通用设计四个方面详细地介绍该方法。

一、三元二次正交三元二次正交是指当设计需要涉及三个变量时，采用三元二次正交设计方法来减少试验次数。

首先将每个变量设为正交系列，进行阶段试验。

然后根据结果分析、确定关键的变量和因素组合，再进行二次设计试验。

二、正交回归设计正交回归设计是一种常用的试验设计方法。

首先将所研究的变量进行正交分组，然后设计正交表，并根据表中的结果确定主要的变量和因素组合。

接着利用回归方法，对组合进行分析和优化。

三、正交设计旋转正交设计旋转是正交试验设计的一种应用，可以对正交表的后续设计进行优化。

在这种方法中，先采用和正交表相同的原始设计方案，然后对因素进行旋转。

旋转后，可以得到一组新的因素组合，也就是新的试验设计方案。

如此重复，直到得出最好的设计方案为止。

四、通用设计在实际工程应用中，可能涉及到多个设计平台。

由于每个平台需要的设计方案都不相同，因此需要一种通用设计方法。

通用设计方法建立在正交设计和正交设计旋转的基础之上。

利用正交试验设计中的随机因素、响应曲面和偏差方案，可以创建一种通用的实验计划，以应用于不同的平台和工程项目。

综上所述，三元二次正交回归旋转通用设计方法是一种高效的工程设计方法，可大幅缩短设计周期、提高工程效率。

对于需要应用多个平台的工程项目来说，这种设计方法更是一种不可少的工具。