一种求解任意信号激励下一阶电路全响应的新方法

第6章一阶电路讲授板书1、理解一阶电路的全响应和阶跃响应概念和物理意义。

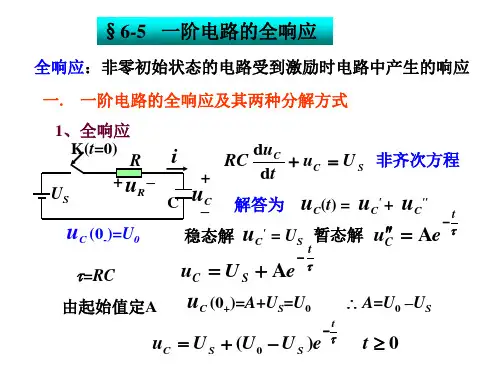
2、掌握一阶电路的全响和阶跃响应的计算方法一阶电路的全响的计算方法一阶电路的阶跃响的计算方法、求解初始值的方法1. 组织教学 5分钟3. 讲授新课70分钟2. 复习旧课5分钟基尔霍夫定律4.巩固新课5分钟5.布置作业5分钟一、学时：2二、班级：06电气工程（本）/06数控技术（本）三、教学内容：[讲授新课]：§6.4一阶电路的全响应一阶电路的全响应是指换路后电路的初始状态不为零，同时又有外加激励源作用时电路中产生的响应。

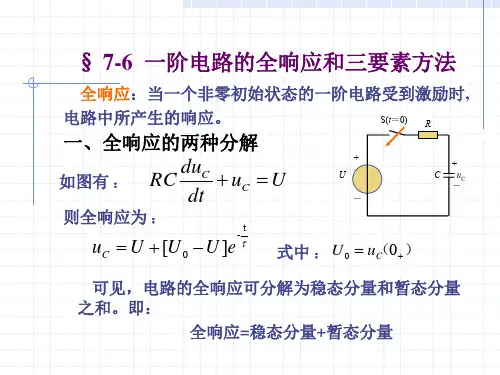
1.全响应以图 6.19 所示的 RC 串联电路为例：图 6.19 图 6.20电路微分方程为：方程的解为：u C(t)=u C＇+ u C＂令微分方程的导数为零得稳态解：u C＂=U S暂态解，其中τ= RC因此由初始值定常数A，设电容原本充有电压：u C(0－)= u C(0+)=U0代入上述方程得：u C(0+)= A + U S = U0解得：A = U0 - U S所以电路的全响应为：2. 全响应的两种分解方式（1）上式的第一项是电路的稳态解，第二项是电路的暂态解，因此一阶电路的全响应可以看成是稳态解加暂态解，即：全响应 = 强制分量 ( 稳态解 )+ 自由分量 ( 暂态解 )（2）把上式改写成：显然第一项是电路的零状态解，第二项是电路的零输入解，因此一阶电路的全响应也可以看成是零状态解加零输入解，即：全响应 = 零状态响应 + 零输入响应此种分解方式便于叠加计算，如图 6.21 所示。

图 6.213. 三要素法分析一阶电路一阶电路的数学模型是一阶微分方程：其解答为稳态分量加暂态分量，即解的一般形式为：t= 0+时有：则积分常数：代入方程得：注意直流激励时：以上式子表明分析一阶电路问题可以转为求解电路的初值f（0+），稳态值f （￥）及时间常数τ的三个要素的问题。

求解方法为：f（0+）：用t → ￥的稳态电路求解；f（￥）：用 0+等效电路求解；时间常数τ：求出等效电阻，则电容电路有τ=RC ，电感电路有:τ= L/R。

一阶动态电路的全响应好嘞，今天我们来聊聊一阶动态电路的全响应。

说到这，大家可能会觉得有点复杂，不过别担心，我会用轻松的方式给你讲明白的。

想象一下，你在家里喝茶，偶尔抬头看看窗外，看到那微风吹过的树叶，忽然想起了电路。

听起来是不是有点奇怪？但电路其实就像生活中的很多事情，有时候一阵风吹来，你的反应会慢半拍，这就跟一阶动态电路一样。

一阶动态电路是什么呢？简单说，就是那种反应不那么迅速的电路。

就像你在思考一件事情时，脑子里可能会卡壳。

电流流动的速度不是瞬间就能达到，而是有个逐渐适应的过程。

就像你早上醒来，不是一下子就能进入状态，得喝杯咖啡，等一等才行。

电路也是，输入信号来了，输出信号得等一等，慢慢才能反应过来。

这种反应过程就叫全响应。

我们来想象一下，一个简单的电路。

假设有个电阻和电容，电压信号突然加上去。

这时候，电容就像个小水库，水库里的水不能一下子装满，得一点点来，慢慢充水。

这个过程就是电容充电的过程，电流逐渐增大，电压也渐渐上升。

你可以把它想象成一个人慢慢适应新环境，刚到一个派对，开始有点紧张，慢慢就能放开来，跟大家聊得热火朝天。

然后啊，电路的全响应不仅仅是充电，放电也是一回事。

电容充好电了，假如这个电源突然断了，电容里的电就像气球里的空气，开始慢慢漏出去。

这时候，电压又会渐渐下降，直到完全放空。

这种变化其实在生活中也很常见，比如你跟朋友聊天，聊得正嗨，结果突然有人打断了，你可能一时没反应过来，脑子里还在回味刚才的话题。

说到这里，可能会有人问，全响应有什么用呢？嘿，这可大有用处了。

你想啊，很多电子设备都需要控制信号的变化速率。

比如说在音响里，如果信号变化太快，可能会造成声音失真，就像是你跟朋友聊天，他话说得太快，你根本跟不上。

反过来，如果反应太慢，又会造成滞后，影响使用体验。

我们再说说这个电路的时间常数。

这个时间常数就像你给电路加个标签，告诉它“嘿，反应时间差不多是多久”。

时间常数越大，反应越慢；越小，反应越快。

关于求解一阶电路的全响应的方法
求解一阶电路的全响应的方法有两种：时域方法和复频域方法。

1. 时域方法：
(a) 首先可以根据电路中的元件参数和初始条件，建立电路的微分方程。

(b) 对电路的微分方程进行求解，得到电路中的电流或电压关于时间的函数表达式。

(c) 根据实际问题中的初始条件，确定积分常数，并代入求解得到的函数表达式中。

(d) 通过得到的电流或电压函数表达式，可以确定电路的全响应。

2. 复频域方法：
(a) 将电路中的元件参数和初始条件通过拉普拉斯变换转换为复频域（s域）。

(b) 对电路的复频域方程进行代数求解，得到电路中的电流或电压的复频域表达式。

(c) 使用拉普拉斯反变换将复频域表达式变换回时域，得到电路中的电流或电压关于时间的函数表达式。

(d) 根据实际问题中的初始条件，确定积分常数，并代入求解得到的函数表达式中。

(e) 通过得到的电流或电压函数表达式，可以确定电路的全响应。

无论是使用时域方法还是复频域方法，求解一阶电路的全响应都需要根据实际情
况确定初始条件，例如电容器或电感器的初始电压或电流，以及连接电路的信号源等。

三元素法分析一阶电路的全响应电路论文学院：电子信息工程学院班级：电气091502班姓名：***学号：************三元素法分析一阶电路的全响应摘要：本文主要介绍用三元素法分析解决一阶电路问题。

用三元素法求一阶电路问题首先要求出三元素：初始值，稳态值，时间常数，用三元素法可以直接代入公式求解，求解过程简单。

关键词：一阶电路 三元素法一、 全响应定义当一个非零初始状态的一阶电路受到激励时，电路的响应称为一阶电路全响应。

全响应总是由初始值、特解和时间常数三个要素决定的。

二、 三元素法的基本原理一阶电路的数学模型是一阶线性微分方程： 其解答一般形式为：令 t = 0+ 全响应f （t ）的三要素求解公式为f （t ）=f （∞）＋[f （0+）－f （∞）]e －t/τ其中，f （0+）为t=0+时刻的初始值，f （∞）为t →∞时的特解稳态值，τ为t ≥0时的时间常数。

f （0+）、f （∞）和τ称为三要素。

只要知道f （0+）、f （∞）和τ这三个要素，就可以根据上述公式直接写出直流激励下一阶电路的全响应，这种方法称为三要素法。

三、 三元素法的解题步骤⒈ 求初始值 ⑴ 初始值定义t=0+时电路中电压与电流的值称为初始值。

⑵ 初始值的求解① 由换路前电路（稳定状态）求u C (0－)和i L (0－)； ② 由换路定律得 u C (0+) 和 i L (0+)。

③ 画0+等效电路。

c bf tfa=+d d τteA t f t f -+'=)()(a.换路后的电路b.电容（电感）用电压源（电流源）替代。

（取0+时刻值，方向与原假定的电容电压、电感电流方向相同）。

④由0+电路求所需各变量的0+值。

⒉求稳态值⑴稳态值的定义t=∞时电路中电压与电流的值称为稳态值。

⑵稳态值的求解稳态时，电容C视为开路，电感L视为短路，稳态值即求直流电阻性电路中的电压和电源。

⒊求时间常数τ⑴时间常数τ的定义当电阻的单位为Ω，电容的单位为F时，乘积RC的单位为s，称为RC电路的时间常数，用τ表示。

方波激励下一阶rc电路响应的研究下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!方波激励下一阶RC电路响应的研究1. 引言在电子工程领域中，RC电路作为最基础且常见的电路之一，其响应特性对于信号处理和滤波至关重要。