变压器的等效电路和向量图

.-电力变压器的参数与数学模型————————————————————————————————作者：————————————————————————————————日期：电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器，假定：绕组电阻为零；因此绕组损耗I2R为零。

铁心磁导率是无穷大，所以铁心磁阻为零。

不计漏磁通；即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:（2-46）磁场强度矢量Hc 为（2-47）其中，磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大，则磁阻R c近似为零。

（2-48）上式可写为：图2-21为双绕组变压器的示意图。

（2-49）或者图2-21中的标记点表示电压E1和E2，在标记点侧是＋极，为同相。

如果图2-21中的其中一个电压极性反向，那么E1与E2相位相差180o。

匝数比k定义如下：理想单相双绕组变压器的基本关系为（2-50）（2-51）由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次侧绕组的复功率为（2-52）代入（2-50）和（2-51）（2-53）可见，流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。

即理想变压器没有有功和无功损耗。

如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连，那么（2-54）这个阻抗，当折算到一次侧时，为（2-55）因此，与二次侧绕组相连的阻抗Z2折算到一次侧，需将Z2乘以匝数比的平方k2。

2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：计及绕组电阻；铁心磁导率为有限值；磁通不完全由铁心构成；计及铁心有功和无功损耗。

图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组，用于计及该绕组损耗I2R。

电抗为一次绕组的漏电抗，串联于一次绕组用于计及一次绕组的漏磁通。

变压器测验题一、电网线电压为66 KV ，经过两台容量均为1500 KVA 的三相变压器二次降压后供给额定电压为400V （Y ）的负载。

第一台： D,y 接，U 1N /U 2N = 66/6.3KV 。

第二台： D,y 接， U 1N /U 2N = 6300/400V 。

两台变压器都在6300伏一侧做短路实验，数据如下：第一台： Uk = 334V , Ik = 137A, p k = 14kW （p 0 =10kW ）第二台： U k =382V , I k =137A, p k =15kW （p 0 =12kW ） 1）画出供电线路图;每台Tr 接为D,y 5(先画相量图)。

2）求出变压器各额定电流?变比？ 3）求每台变压器的短路阻抗标幺值？4）画出从66KV 侧看的简化等效电路和向量图 ；5）当原边加额定电压，每相负载阻抗Z l =0.1+j0.07Ω（Y 接）时，负载的电流？ 6）求上述情况下各变压器效率及总效率？并求出总的电压变化率？ 二、画出下图变压器电动势相量图，并判断其联结组别。

三、画出D /Y-7联接组别接线图和相量图。

四、一台Y/Δ接的三相变压器空载运行，,原方（高压侧）加上对称的正弦额定电压，试分析下列物理量中有无三次谐波。

1）主磁通。

2）原、副方相电势。

3）原、副方线电压；原、副方相电压。

4）原、副方线电流；原、副方相电流。

五、现有一个万用表和一个可调交流电压源，说明如何判断同一芯柱上的高低压绕组的同极性端。

六、一台2kV·A ，400/100V 的单相变压器，低压侧加100V ，高压侧开路，测得I 0=2A ；p 0=20W ；当高压侧加400V ，低压侧开路，测得I 0= A ，p 0=W 。

七、变压器铁心导磁性能越好，其励磁电抗 ，励磁电流 。

八、某人初次使用互感器对巨型三相变压器进行短路实验。

由于变压器是高电压、大电流，因此需要借助电压互感器和电流互感器来完成。

一般系统不平衡电压较大时，Z型变压器的三相绕组做成平衡式，就可以满足测量需要。

当系统不平衡电压较小时，Z型变压器的中性点要做出30V～70V的不平衡电压以满足测量需要。

接地变压器除可带消弧线圈外，也可带二次负载，代替站用变。

在带二次负载时，接地变压器的一次容量应为消弧线圈容量与二次负载容量之和。

接地变的最大功能就是传递接地补偿电流。

Z型接地变压器的接线有ZNyn11（如下图）和ZNyn1有两种接线方式。

其降低零序阻抗的原理是：在接地变压器三相铁芯的每一相都有两个匝数相同的绕组，分别接不同的相电压。

当接地变压器线端加入三相正、负序电压时，接地变压器每一铁芯柱上产生的磁势是两相绕组磁势的向量和。

三个铁芯柱上的合成磁势相差120°，是一组三相平衡量。

三相磁通可在三个铁芯柱上互相形成磁通路，磁阻小、磁通量大、感应电势大，呈现很大的励磁阻抗。

当接地变压器三相线端加入零序电压时，在每个铁芯柱上的两个绕组产生的磁势大小相等，方向相反，合成的磁势为零，三相铁芯柱上没有零序磁通。

零序磁通只能通过外壳和周围介质形成闭合回路，磁阻很大，零序磁通很小，所以零序阻抗也很小。

接地变压器的作用是在系统为△型接线或Y型接线中性点无法引出时，引出中性点用于加接消弧线圈，该变压器采用Z型接线（或称曲折型接线），与普通变压器的区别是每相线圈分别绕在两个磁柱上，这样连接的好处是零序磁通可沿磁柱流通，而普通变压器的零序磁通是沿着漏磁磁路流通，所以Z型接地变压器的零序阻抗很小（10Ω左右），而普通变压器要大得多。

Z形接线具有如下优点:1,允许中点载流的负载且有较低的零序阻抗2,可用作接地变压器的接法形成人工中点3,可降低系统中的电压不平衡.4,具有良好的防雷特性对于35KV、66KV配电网，变压器绕组通常采用Y接法，有中性点引出，就不需要使用接地变压器。

对于6KV、10KV配电网，变压器绕组通常采用△接法，无中性点引出，这就需要用接地变压器引出中性点。

变压器原理§变压器基本工作原理、结构与额定数据一、理想变压器的运行原理：{2111eeiu→→→φ·变压器电动势：匝数为N的线圈环链φ，当φ变化时，线圈两端感生电动势e的大小与N及dd tφ成正比，方向由楞次定律决定。

·楞次定律：在变化磁场中线圈感应电动势的方向总是使它推动的电流产生另一个磁场，阻止原有磁场的变化。

U2＋－变压器的基本结构U1高U1+ e1=0一次侧等效电路(假定一次侧线圈电阻值为零)e22U2－e2=0二次侧等效电路·假设：1、一二次侧完全耦合无漏磁，忽略一二次侧线圈电阻；2、忽略铁心损耗；3、忽略铁心磁阻；4、1U为正弦电压。

·假定正向：电动势是箭头指向为高，电压是箭头指向为低。

·主磁通方向由一次侧励磁电流和绕组缠绕方向通过右手螺旋法则确定。

·一次侧感应电动势的符号：由它推动的电流应当与励磁电流方向相反，所以它的实际方向应当高电位在上，图中的假定正向与实际方向相反，故有dtd e 1Φ-=N 1 ·二次侧感应电动势的符号：由它推动的电流应当阻止主磁通的变化，即按右手螺旋法则应当产生与主磁通方向相反的磁通，按图中副方绕组的缠绕方向，它的实际方向也应当高电位在上，图中的假定正向与实际方向也相反，所以有dtd Ne 2Φ-=2，一二次侧感应电动势同相位。

而按照电路理论，有u e u e 1122=-=·变压器的电压变比21212121e U U E E N N e e K ====·因为假定铁心损耗为零，故有变压器一二次侧视在功率相等：2I =U I U 211,故e K I I 121= ·L e L LZ K I U Z , I U Z 21122===∧ ·变压器的功能是在实现对电压有效值变换的同时， 还实现了对电流有效值和阻抗大小的变换。

二、基本结构〖阅读〗 三、额定数据·S N ：额定工况下输出视在功率保证值。

变压器等效电路变压器是电力系统中常用的重要设备，用于改变交流电压的大小。

在电力系统中，为了进行电路分析和计算，可以采用等效电路模型来表示变压器的工作原理和性能。

本文将介绍变压器等效电路的基本原理和常见模型。

1. 变压器的基本原理变压器是由一个或多个线圈组成的，通过电磁感应的原理来改变电压。

变压器由铁心和绕组组成。

绕组分为初级绕组和次级绕组，通过将电流通过初级绕组，产生的磁场会感应到次级绕组，从而改变输出电压的大小。

变压器的基本原理是基于法拉第电磁感应定律。

2. 变压器的等效电路模型为了简化电路分析和计算，可以采用等效电路模型来代替变压器。

常见的变压器等效电路模型有两种：简化型和精确型。

2.1 简化型等效电路模型简化型等效电路模型将变压器抽象为两个卷绕电感和一个理想变压器，分别代表初级绕组和次级绕组的电感和变压器的变换关系。

在这个模型中，忽略了变压器的内阻和铁芯的磁滞特性。

2.2 精确型等效电路模型精确型等效电路模型更加符合实际变压器的工作原理，考虑了变压器的内阻和铁芯的磁滞特性。

在这个模型中，将变压器抽象为两个卷绕电感、两个卷绕电阻和一个理想变压器。

通过考虑内阻和磁滞特性，可以更加准确地描述变压器的电特性。

3. 变压器等效电路模型的参数无论是简化型还是精确型等效电路模型，都需要知道一些参数来描述变压器的性能。

常见的参数有：3.1 变压器的变比变比是指变压器的输入电压与输出电压的比值。

例如，变比为2：1表示输出电压是输入电压的两倍。

3.2 变压器的电感电感是指变压器的绕组对电流变化的阻抗。

初级绕组和次级绕组的电感分别表示为L1和L2。

3.3 变压器的内阻内阻是指变压器绕组的电阻。

初级绕组和次级绕组的内阻分别表示为R1和R2。

4. 变压器等效电路的应用变压器等效电路模型可以应用于电力系统的分析和计算中。

通过使用等效电路模型，可以更加方便地处理变压器与其他电路元件之间的相互作用。

4.1 电路分析变压器等效电路模型可以与其他电路元件一起进行电路分析，例如，计算电流、电压、功率等参数。

.-电力变压器的参数与数学模型————————————————————————————————作者：————————————————————————————————日期：电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器，假定：绕组电阻为零；因此绕组损耗I2R为零。

铁心磁导率是无穷大，所以铁心磁阻为零。

不计漏磁通；即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:（2-46）磁场强度矢量Hc 为（2-47）其中，磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大，则磁阻R c近似为零。

（2-48）上式可写为：图2-21为双绕组变压器的示意图。

（2-49）或者图2-21中的标记点表示电压E1和E2，在标记点侧是＋极，为同相。

如果图2-21中的其中一个电压极性反向，那么E1与E2相位相差180o。

匝数比k定义如下：理想单相双绕组变压器的基本关系为（2-50）（2-51）由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次侧绕组的复功率为（2-52）代入（2-50）和（2-51）（2-53）可见，流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。

即理想变压器没有有功和无功损耗。

如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连，那么（2-54）这个阻抗，当折算到一次侧时，为（2-55）因此，与二次侧绕组相连的阻抗Z2折算到一次侧，需将Z2乘以匝数比的平方k2。

2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：计及绕组电阻；铁心磁导率为有限值；磁通不完全由铁心构成；计及铁心有功和无功损耗。

图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组，用于计及该绕组损耗I2R。

电抗为一次绕组的漏电抗，串联于一次绕组用于计及一次绕组的漏磁通。

变压器的3种等效电路变压器是一种常见的电力设备，用于改变交流电的电压。

它可以将高压电能转换为低压电能，或者将低压电能升高为高压电能。

变压器的工作原理是基于电磁感应的原理，通过电磁感应现象来实现电压的转换。

在实际应用中，我们可以用三种等效电路来描述变压器的工作原理。

第一种等效电路是理想变压器等效电路。

理想变压器等效电路是基于理想变压器模型，假设变压器的磁路没有磁阻，变压器的线圈没有电阻，变压器的磁化曲线是线性的。

在理想变压器等效电路中，变压器的主要参数是变比，即输入电压和输出电压之间的比值。

理想变压器等效电路可以用于计算变压器的电压、电流和功率等参数。

但是在实际应用中，变压器的磁路存在磁阻，线圈存在电阻，因此理想变压器等效电路只是一个简化模型，不能完全描述变压器的实际工作情况。

第二种等效电路是短路阻抗等效电路。

短路阻抗等效电路是在理想变压器等效电路的基础上考虑了变压器的短路阻抗。

短路阻抗是指变压器的二次侧短路时，二次侧电压与短路电流之比。

短路阻抗等效电路可以用于计算变压器的短路电流和短路功率损耗等参数。

短路阻抗等效电路在变压器的设计和保护中具有重要的应用价值。

第三种等效电路是电压漏电抗等效电路。

电压漏电抗等效电路是在理想变压器等效电路的基础上考虑了变压器的漏电抗。

漏电抗是指变压器的一次侧电压与一次侧电流之比。

电压漏电抗等效电路可以用于计算变压器的负载电流和负载功率损耗等参数。

电压漏电抗等效电路在变压器的设计和运行中起着重要的作用。

变压器的工作原理可以用三种等效电路来描述。

理想变压器等效电路适用于计算变压器的基本参数，短路阻抗等效电路适用于计算变压器的短路电流和短路功率损耗，电压漏电抗等效电路适用于计算变压器的负载电流和负载功率损耗。

这三种等效电路相互补充，共同构成了对变压器工作原理的全面描述。

在实际应用中，我们可以根据需要选择适合的等效电路进行计算和分析，以确保变压器的安全运行和高效工作。

变压器等效电路推导变压器是一种常用于电力传输和电子设备中的重要电气设备。

在实际应用中，为了便于分析和计算，我们常常将变压器简化为等效电路。

本文将从基本原理出发，推导变压器的等效电路。

我们需要了解变压器的基本结构和原理。

一个典型的变压器由两个线圈（即绕组）和一个铁芯组成。

其中一个线圈称为主绕组，通常用来输入电能；另一个线圈称为副绕组，用来输出电能。

铁芯则起到了导磁作用，用来传导磁场。

在变压器工作时，主绕组中通过的电流会产生一个磁场，磁场经过铁芯传导到副绕组中，从而在副绕组中感应出电压。

根据法拉第电磁感应定律，感应电压与磁通量的变化率成正比。

因此，当主绕组中的电流变化时，副绕组中的电压也会相应变化。

为了分析变压器的等效电路，我们需要引入一些假设和简化。

首先，假设变压器的所有绕组都是理想的，即没有电阻和电感。

其次，假设铁芯的导磁特性是线性的，即磁通量与磁场强度成正比。

基于以上假设，我们可以推导出变压器的等效电路。

首先，我们将主绕组和副绕组分别用电感元件表示，分别记为L1和L2。

由于绕组是理想的，所以它们之间没有电阻。

此外，由于铁芯的线性导磁特性，我们可以用一个互感元件表示铁芯，记为M。

在等效电路中，我们还需要考虑变压器的变比。

变比是指主绕组和副绕组之间的匝数比。

假设变比为k，即主绕组的匝数是副绕组的k 倍。

由于变比的存在，我们需要在等效电路中引入一个变压器的变比变压器，记为K。

根据以上分析，我们可以得到变压器的等效电路如下图所示：```L1------]--------[-----]----| | || | |M1 | || | || | || | |------]--------[-----]----L2```在等效电路中，L1和L2分别表示主绕组和副绕组的电感，M1表示铁芯的互感，K表示变比变压器。

值得注意的是，变比变压器的变比为k，即主绕组与副绕组之间的匝数比。

通过这个等效电路，我们可以方便地分析变压器的工作原理和特性。

变压器的等效电路和向量图•2009-09-26 23:16:48 标签Tag：•1224人阅读一变压器的折算法将变压器的副边绕组折算到原边，就是用一个与原绕组匝数相同的绕组，去代替匝数为N2的副绕组，在代替的过程中，保持副边绕组的电磁关系及功率关系不变。

二参数折算折算前原边N1 U1 I1 E1 R1 X1σ副边N2 U2 I2 E2 R2 X2σRL XL折算后原边N1 U1 I1 E1 R1 X1σ副边N2' U2' I2' E2' R2' X2σ'RL' XL'变压器副绕组折算到原边后其匝数为N1，折算后的副边各量加“ ' ”以区别折算前的各量。

1 电势折算E2'＝4.44fN1Фm＝E1E2＝4.44fN2Фm所以E2'/E2＝N1/N2＝k，E2＝kE2折算前后电磁关系不变，那么铁心中的磁通不变，k为变比，也即是电势，电压折算的系数2 磁势折算N1I2'=N2I2=I2N2/N1=I2/k变压器折算前后副绕组磁势不变。

k也为电流折算系数。

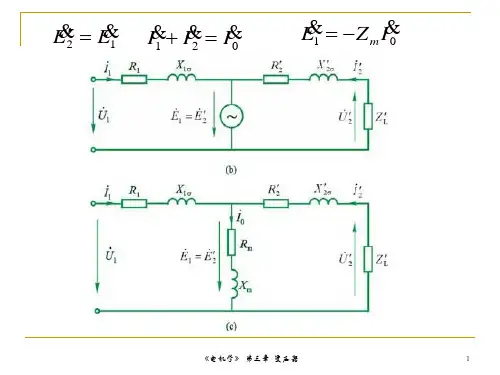
3 阻抗折算阻抗折算要保持功率不变折算前后副边铜耗不变I2'I2'R2'＝I2I2R2R2'=(I2/I2')(I2/I2')R2=kkR2(kk)---阻抗折算系数副边漏抗上的无功功率不变，则I2'I2'X2σ'=I2I2X2σX2σ'=(I2/I2')(I2/I2')X2σ=kkX2σ负载阻抗上的功率不变，则可求出I2'I2'RL'=I2I2RL RL'=kkRLI2'I2'XL'=I2I2XL XL'=kkXL4 副边电压折算u2'=I2'ZL'=(I2/k)(RL+jXL)kk=kI2（RL+jXL）=kU2三变压器的等效电路折算后方程U1=－E1＋I1（R1＋jX1σ）U2'=E2'－I2'（R2＋jX2σ）I1+I2'=Im≈I0－E1=－E2=Im(Rm+jXm)=ImZm折算后电压平衡方程式，磁势平衡方程式及励磁回路等效电路如上面4个式子所示，这些式子为变压器的基本方程式。