变压器的等效电路

变压器t型等效电路各参数的物理意义变压器是一种常见的电气设备，用于改变交流电的电压。

而T型等效电路是一种用于描述变压器工作原理的电路模型。

本文将从T型等效电路中各参数的物理意义出发，介绍变压器的工作原理和性能。

我们来了解一下T型等效电路的结构。

T型等效电路由两个电感L1和L2以及一个互感M组成。

其中，电感L1和L2分别代表变压器的主线圈和副线圈，互感M则表示两个线圈之间的耦合程度。

1. 电感L1和L2的物理意义：电感是指电流通过时，产生磁场的能力。

在变压器中，主线圈和副线圈分别由电感L1和L2表示。

电感的大小与线圈的匝数、线圈的尺寸以及线圈中的磁性材料有关。

电感L1和L2的值越大，代表线圈具有更强的磁场产生能力。

2. 互感M的物理意义：互感是指两个线圈之间通过磁场相互耦合的程度。

在变压器中，主线圈和副线圈之间的互感由互感M表示。

互感的大小与两个线圈之间的距离、线圈的匝数以及线圈中的磁性材料有关。

互感M的值越大，代表两个线圈之间的耦合程度越强。

3. 变压器的变比和转向比：变压器的变比指的是主线圈和副线圈的匝数比，用N1/N2表示。

变比越大，代表变压器可以将输入电压转换为更高的输出电压。

转向比指的是副线圈中的电流与主线圈中的电流的比值，用I2/I1表示。

转向比越大，代表变压器可以将输入电流转换为更小的输出电流。

4. 变压器的工作原理：当变压器接通交流电源后，主线圈中的电流会产生磁场。

由于互感的存在，这个磁场会通过铁芯传导到副线圈中。

在副线圈中，根据电磁感应定律，磁场的变化会引起电动势的产生，从而产生输出电流。

通过变压器的变比和转向比，可以将输入电压和电流转换为所需的输出电压和电流。

5. 变压器的效率和损耗：变压器的效率是指输出功率与输入功率的比值，用η表示。

变压器的损耗包括铁心损耗和线圈损耗。

铁心损耗是指由于铁芯的磁滞和涡流效应而产生的能量损耗。

线圈损耗是指由于线圈中电流通过时产生的电阻损耗。

变压器的效率和损耗与变压器的设计和材料有关，通常会通过优化设计和选择低损耗材料来提高变压器的效率。

变压器等效电路变压器是电力系统中常用的重要设备，用于改变交流电压的大小。

在电力系统中，为了进行电路分析和计算，可以采用等效电路模型来表示变压器的工作原理和性能。

本文将介绍变压器等效电路的基本原理和常见模型。

1. 变压器的基本原理变压器是由一个或多个线圈组成的，通过电磁感应的原理来改变电压。

变压器由铁心和绕组组成。

绕组分为初级绕组和次级绕组，通过将电流通过初级绕组，产生的磁场会感应到次级绕组，从而改变输出电压的大小。

变压器的基本原理是基于法拉第电磁感应定律。

2. 变压器的等效电路模型为了简化电路分析和计算，可以采用等效电路模型来代替变压器。

常见的变压器等效电路模型有两种：简化型和精确型。

2.1 简化型等效电路模型简化型等效电路模型将变压器抽象为两个卷绕电感和一个理想变压器，分别代表初级绕组和次级绕组的电感和变压器的变换关系。

在这个模型中，忽略了变压器的内阻和铁芯的磁滞特性。

2.2 精确型等效电路模型精确型等效电路模型更加符合实际变压器的工作原理，考虑了变压器的内阻和铁芯的磁滞特性。

在这个模型中，将变压器抽象为两个卷绕电感、两个卷绕电阻和一个理想变压器。

通过考虑内阻和磁滞特性，可以更加准确地描述变压器的电特性。

3. 变压器等效电路模型的参数无论是简化型还是精确型等效电路模型，都需要知道一些参数来描述变压器的性能。

常见的参数有：3.1 变压器的变比变比是指变压器的输入电压与输出电压的比值。

例如，变比为2：1表示输出电压是输入电压的两倍。

3.2 变压器的电感电感是指变压器的绕组对电流变化的阻抗。

初级绕组和次级绕组的电感分别表示为L1和L2。

3.3 变压器的内阻内阻是指变压器绕组的电阻。

初级绕组和次级绕组的内阻分别表示为R1和R2。

4. 变压器等效电路的应用变压器等效电路模型可以应用于电力系统的分析和计算中。

通过使用等效电路模型，可以更加方便地处理变压器与其他电路元件之间的相互作用。

4.1 电路分析变压器等效电路模型可以与其他电路元件一起进行电路分析，例如，计算电流、电压、功率等参数。

变压器励磁电感等效电路
首先，让我们来看看励磁电感等效电路的基本结构。

该电路通常包括一个电感元件，代表了变压器的主磁路的磁感应强度，以及一个电阻元件，代表了磁芯中的铁损耗和涡流损耗。

这两个元件一起构成了励磁电感等效电路的基本模型。

其次，让我们来探讨一下励磁电感等效电路的作用。

励磁电感等效电路可以帮助工程师和研究人员更好地理解变压器在励磁状态下的电气特性，包括磁化曲线、励磁电流和励磁电压之间的关系。

通过这个等效电路模型，我们可以更好地分析和计算变压器在实际工程中的性能。

此外，励磁电感等效电路还可以用于仿真和计算。

在电力系统分析和设计中，我们经常需要对变压器在不同工况下的响应进行仿真和计算。

励磁电感等效电路可以作为一个简化的模型，帮助我们进行这些仿真和计算工作。

最后，让我们来思考一下励磁电感等效电路的局限性。

虽然励磁电感等效电路可以很好地描述变压器的励磁特性，但它仍然是一个简化模型，无法完全准确地反映变压器的复杂行为。

在实际工程
中，我们可能还需要考虑更多的因素，如温升效应、饱和效应等。

因此，在使用励磁电感等效电路进行分析和设计时，我们需要注意其局限性，并结合实际情况进行综合考虑。

总的来说，励磁电感等效电路是描述变压器在励磁状态下电气特性的重要模型，它有助于我们更好地理解和分析变压器的性能，但在实际应用中仍需谨慎对待其简化模型的局限性。

变压器去耦等效电路概述变压器去耦等效电路是一种常用的电子电路，用于去除输入和输出之间的直流偏置，使得信号能够在变压器上进行传输。

该电路通过使用一个变压器和适当的电容来实现。

本文将详细介绍变压器去耦等效电路的原理、设计和应用。

原理在电子电路中，变压器被广泛用于信号传输和电源转换。

变压器去耦等效电路利用了变压器的特性，将输入和输出之间的直流信号隔离开来，只允许交流信号通过。

这样可以消除直流偏置，提高信号的质量和稳定性。

变压器去耦等效电路通常由两部分组成：一个变压器和一个耦合电容。

变压器的作用是将输入和输出之间的直流信号隔离开来，只允许交流信号通过。

耦合电容则用于连接变压器的输入和输出端口，使得交流信号能够在变压器上进行传输。

设计设计一个合适的变压器去耦等效电路需要考虑以下几个方面：1. 输入和输出的电压和电流要求：根据具体的应用需求，确定输入和输出的电压和电流范围。

2. 变压器的参数选择：根据输入和输出的电压和电流要求，选择合适的变压器。

变压器的参数包括变比、绕组数、磁芯材料等。

3. 耦合电容的选择：根据变压器的特性和输入输出的频率范围，选择合适的耦合电容。

耦合电容的参数包括容值、电压等级等。

4. 电路布局和连接：将变压器和耦合电容按照设计要求进行布局和连接。

注意保持电路的良好接地和信号传输的可靠性。

应用变压器去耦等效电路广泛应用于各种电子设备和系统中，特别是在需要信号传输和电源转换的场合。

以下是一些常见的应用场景：1. 音频设备：在音频放大器和扬声器系统中，变压器去耦等效电路可以提高音频信号的质量和稳定性。

2. 通信系统：在通信设备和系统中，变压器去耦等效电路可以隔离输入和输出之间的直流偏置，提高信号传输的可靠性和抗干扰能力。

3. 电源转换器：在电源转换器中，变压器去耦等效电路可以隔离输入和输出之间的直流偏置，保护负载和电源的安全。

4. 仪器仪表：在各种仪器仪表中，变压器去耦等效电路可以提供稳定的信号传输和精确的测量结果。

李勇电机学变压器的等效电路李勇，电机学老师，是我们学校中备受尊敬的一位教授。

在他的教学中，他善于将抽象的理论知识转化为生动而有趣的例子和实验，以此激发学生对电机学的兴趣和热情。

今天，我将重点介绍他在教授变压器等效电路方面所做的贡献。

变压器是电力系统中很重要的一种设备，它主要用于变换电压和电流。

理解变压器的工作原理以及其等效电路是电机学学习中必不可少的内容。

李勇老师在讲解变压器等效电路时，一般将其分为两个部分：一是变压器的实际电路，二是变压器的等效电路。

变压器的实际电路包括磁路和电路两部分。

其中，磁路是由磁芯和线圈的铁芯构成的，而电路则是由变压器的线圈和电源的电路组成的。

李勇老师在教学中强调了磁通量是变压器中重要的物理量，它可以用来描述磁路中所有的磁通量的总和。

磁通量的大小与磁通量密度有关，与磁芯材料、长度和截面积等因素有关。

变压器的等效电路则是将变压器的实际电路简化为一组等效电路元件。

等效电路的理论基础是基尔霍夫电压定律和基尔霍夫电流定律。

通过等效电路，可以将实际电路抽象为一个更简单的电路模型，从而方便分析和计算。

等效电路中的元件包括电阻、电感和电压源等部分。

李勇老师在教学中详细介绍了变压器的等效电路中的各个元件的参数。

首先是变压器的阻抗，它与变压器的线圈参数有关。

阻抗是反映电路中电流通过时所遇到的阻力的物理量，它的大小与线圈的电阻和感抗有关。

在等效电路中，变压器的阻抗常常以电感和电阻的综合形式出现。

变压器的阻抗会影响变压器的效率和损耗。

其次是变压器的互感。

互感用来描述变压器的两个线圈间的相互作用关系。

互感的大小取决于两个线圈的匝数和它们之间的距离。

当变压器处于工作状态时，通常会将互感视为理想互感，这样等效电路中只需要考虑一对理想互感即可。

最后是变压器的电压比。

电压比是变压器中最基本的参数之一，它描述了变压器输入电压与输出电压之间的关系。

电压比的大小由变压器的匝比决定。

在等效电路中，通常将变压器的电压比表示为变比，变比等于输出电压除以输入电压。

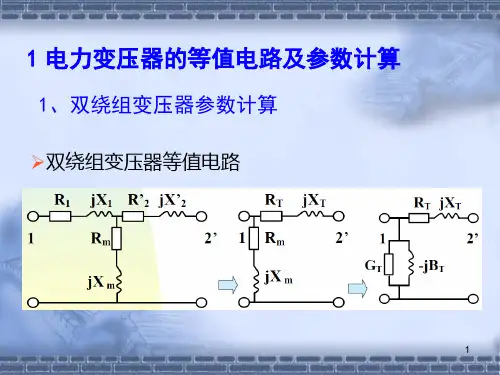
变压器的基本方程和等效电路一、变压器的基本方程负载运行时，变压器内部的磁动势、磁通和感应电动势，可列表归纳如下：此外，一次和二次绕组内还有电阻压降i1R1和i2R2。

这样，根据基尔霍夫第二定律和图2-8中所示的正方向，即可写出一次和二次侧的电压方程为若一次和二次的电压、电流均随时间正弦变化，则上式可写成相应的复数形式式中，Z1σ和Z2σ分别称为一次和二次绕组的漏阻抗，Z1σ＝R1十jX1σ，Z2σ=R2十jX2σ再考虑到式(2—12)和磁动势方程(2—17)，可得变压器的基本方程为二、变压器的等效电路在研究变压器的运行问题时，希望有一个既能正确反映变压器内部电磁关系，又便于工程计算的等效电路，来代替具有电路、磁路和电磁感应联系的实际变压器。

下面从变压器的基本方程出发，导出此等效电路。

绕组归算为建立等效电路，除了需要把一次和二次侧漏磁通的效果作为漏抗压降，主磁通和铁心线圈的效果作为激磁阻抗来处理外，还需要进行绕组归算，通常是把二次绕组归算到一次绕组，也就是假想把二次绕组的匝数变换成一次绕组的匝数，而不改变一次和二次绕组原有的电磁关系。

从磁动势平衡关系可知，二次电流对一次侧的影响是通过二次磁动势N2I2起作用，所以只要归算前后二次绕组的磁动势保持不变，一次绕组将从电网吸收同样大小的功率和电流，并有同样大小的功率传递给二次绕组。

归算后．二次侧各物理量的数值称为归算值，用原物理量的符号加“′”来表示。

设二次绕组电流和电动势的归算值为­­­­′和′，根据归算前、后二次绕组磁动势不变的原则，可得由此可得二次电流的归算值­­­­′为由于归算前、后二次绕组的磁动势未变，因此铁心中的主磁通将保持不变；这样，根据感应电动势与匝数成正比这一关系，便得即二次绕组感应电动势的归算值′为再把二次绕组的电压方程(式(2—22)中的第二式)乘以电压比k，可得式中，R2′和X2σ′分别为二次绕组电阻和漏抗的归算值，R2′＝k2R2，X2σ′= k2X2σ；′则是二次电压的归算值，′＝k。

变压器的3种等效电路变压器是一种常见的电力设备，用于改变交流电的电压。

它可以将高压电能转换为低压电能，或者将低压电能升高为高压电能。

变压器的工作原理是基于电磁感应的原理，通过电磁感应现象来实现电压的转换。

在实际应用中，我们可以用三种等效电路来描述变压器的工作原理。

第一种等效电路是理想变压器等效电路。

理想变压器等效电路是基于理想变压器模型，假设变压器的磁路没有磁阻，变压器的线圈没有电阻，变压器的磁化曲线是线性的。

在理想变压器等效电路中，变压器的主要参数是变比，即输入电压和输出电压之间的比值。

理想变压器等效电路可以用于计算变压器的电压、电流和功率等参数。

但是在实际应用中，变压器的磁路存在磁阻，线圈存在电阻，因此理想变压器等效电路只是一个简化模型，不能完全描述变压器的实际工作情况。

第二种等效电路是短路阻抗等效电路。

短路阻抗等效电路是在理想变压器等效电路的基础上考虑了变压器的短路阻抗。

短路阻抗是指变压器的二次侧短路时，二次侧电压与短路电流之比。

短路阻抗等效电路可以用于计算变压器的短路电流和短路功率损耗等参数。

短路阻抗等效电路在变压器的设计和保护中具有重要的应用价值。

第三种等效电路是电压漏电抗等效电路。

电压漏电抗等效电路是在理想变压器等效电路的基础上考虑了变压器的漏电抗。

漏电抗是指变压器的一次侧电压与一次侧电流之比。

电压漏电抗等效电路可以用于计算变压器的负载电流和负载功率损耗等参数。

电压漏电抗等效电路在变压器的设计和运行中起着重要的作用。

变压器的工作原理可以用三种等效电路来描述。

理想变压器等效电路适用于计算变压器的基本参数，短路阻抗等效电路适用于计算变压器的短路电流和短路功率损耗，电压漏电抗等效电路适用于计算变压器的负载电流和负载功率损耗。

这三种等效电路相互补充，共同构成了对变压器工作原理的全面描述。

在实际应用中，我们可以根据需要选择适合的等效电路进行计算和分析，以确保变压器的安全运行和高效工作。

变压器接直流电源的等效电路
变压器接直流电源的等效电路通常是一个电阻和一个电动势的串联。

首先，变压器的主要作用是将交流电源的电压变换成需要的电压，而不是直接将直流电源的电压变换。

因此，在变压器接直流电源时，我们需要添加一个电阻来模拟电阻性质的交流负载。

这个电阻会消耗掉直流电源的电流，并产生热量。

电动势可以用一个电池或者一个恒流源来表示，它的作用是提供所需的直流电压。

因此，变压器接直流电源的等效电路可以表示为：
直流电源 ---- 电动势 ---- 电阻 ---- 变压器
需要注意的是，在实际应用中，变压器通常被设计为适应交流电源而不是直流电源，因此将变压器直接连接在直流电源上可能会导致不正常的工作或损坏变压器。

如果需要将直流电源的电压变换，可以使用直流-直流变换器或直流-交流-直流变换器。