变压器等效模型

第二节变压器的参数和数学模型⏹双绕组变压器的参数和数学模型⏹三绕组变压器的参数和数学模型⏹自耦变压器的参数和数学模型一.双绕组变压器的参数和数学模型⏹阻抗⏹电阻变压器的电阻是通过变压器的短路损耗，其近似等于额定总铜耗。

我们通过如下公式来求解变压器电阻：（MV A）Rt—电阻（欧）•电抗在电力系统计算中认为，大容量变压器的电抗和阻抗在数值上接近相等，可近似如下求解：Uk —阻抗电压（%），Un —额定电压（kV ），Sn —额定容量（MV A ） Xt —电抗⏹导纳⏹电导 变压器电导对应的是变压器的铁耗，近似等于变压器的空载损耗，因此变压器的电导可如下求解：⏹电纳在变压器中，流经电纳的电流和空载电流在数值上接近相等，其求解如下：二.三绕组变压器的参数和数学模型⏹按三个绕组容量比的不同有三种不同的类型：100/100/100、100/50/100、100/100/50⏹按三个绕组排列方式的不同有两种不同的结构：升压结构：中压内，低压中，高压外降压结构：低压内，中压中，高压外•电阻由于容量的不同，对所提供的短路损耗要做些处理 ⏹⏹对于100/50/100或100/100/50首先，将含有不同容量绕组的短路损耗数据归算为额定电流下的值。

例如：对于100/50/100然后，按照100/100/100计算电阻的公式计算各绕组电阻。

2. 电抗⏹根据变压器排列不同，对所提供的短路电压做些处理：一般来说，所提供的短路电压百分比都是经过归算的三.自耦变压器的参数和数学模型就端点条件而言，自耦变压器可完全等值于普通变压器，但由于三绕组自耦变压器第三绕组的容量总小于变压器的额定容量，因此需要进行归算。

❖对于旧标准：❖对于新标准，也是按最大短路损耗和经过归算的短路电压百分比值进行计算。

第二章 电力系统各元件的特性和数学模型一．电力线路的参数和数学模型二．负荷的参数和数学模型第三节 电力线路的参数和数学模型⏹电力线路结构简述电力线路按结构可分为架空线：导线、避雷线、杆塔、绝缘子和金具等电缆：导线、绝缘层、保护层等架空线路的导线和避雷线导线：主要由铝、钢、铜等材料制成避雷线：一般用钢线1. 架空线路的导线和避雷线❖认识架空线路的标号×××××—×/×钢线部分额定截面积主要载流部分额定截面积J 表示加强型，Q表示轻型J 表示多股线表示材料，其中：L表示铝、G表示钢、T表示铜、HL表示铝合金例如：LGJ—400/50表示载流额定截面积为400、钢线额定截面积为50的普通钢芯铝线。

.-电力变压器的参数与数学模型————————————————————————————————作者：————————————————————————————————日期：电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器，假定：绕组电阻为零；因此绕组损耗I2R为零。

铁心磁导率是无穷大，所以铁心磁阻为零。

不计漏磁通；即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:（2-46）磁场强度矢量Hc 为（2-47）其中，磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大，则磁阻R c近似为零。

（2-48）上式可写为：图2-21为双绕组变压器的示意图。

（2-49）或者图2-21中的标记点表示电压E1和E2，在标记点侧是＋极，为同相。

如果图2-21中的其中一个电压极性反向，那么E1与E2相位相差180o。

匝数比k定义如下：理想单相双绕组变压器的基本关系为（2-50）（2-51）由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次侧绕组的复功率为（2-52）代入（2-50）和（2-51）（2-53）可见，流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。

即理想变压器没有有功和无功损耗。

如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连，那么（2-54）这个阻抗，当折算到一次侧时，为（2-55）因此，与二次侧绕组相连的阻抗Z2折算到一次侧，需将Z2乘以匝数比的平方k2。

2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：计及绕组电阻；铁心磁导率为有限值；磁通不完全由铁心构成；计及铁心有功和无功损耗。

图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组，用于计及该绕组损耗I2R。

电抗为一次绕组的漏电抗，串联于一次绕组用于计及一次绕组的漏磁通。

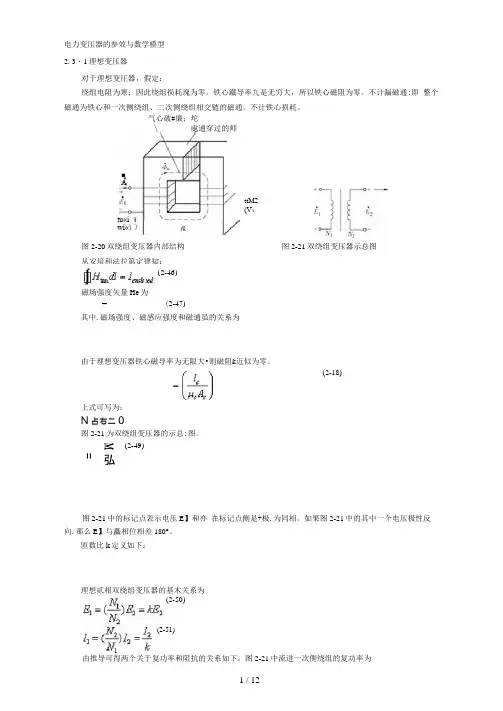
电力变压器的参效与数学模型 2. 3・1理想变压器对于理想变圧器，假定：绕组电阻为寒：因此绕组损耗瑰为零。

铁心鐵导率九是无穷大，所以铁心磁阻为零。

不计漏磁通:即 整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

其中.磁场强度、磁感应强度和磁通虽的关系为由于理想变压器铁心磁导率为无限大•则磁阻&近似为零。

(2-18)上式可写为：N 占右二0图2-21为双绕组变压器的示总:图。

(2-49)图2-21中的标记点表示电压E 】和亦 在标记点侧是+极.为同相。

如果图2-21中的其中一个电压极性反向.那么E 】与矗相位相差180°。

匝数比k 定义如下：理想贰相双绕组变压器的基木关系为由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次側绕组的复功率为图2-20双绕组变压器内部结构 图2-21双绕组变压器示总图(2-46) M弘=耳瓦■A气心破#廉；坨 \ 處通穿过的师tu«i wi«)ttM2 (V ：H>fk从安培和法拉第定律知：磁场强度矢量He 为= (2-47)(2-50)(2-51)£ =爲Z ；（2・52） 代入（2-50）和（2-51）S 严即;二姫訊令二即;二鸟 (2-53)可见，流进一次侧绕组的复功率S 】与流岀二次侧绕组的复功率$相等。

即理想变压器没有有功和无功损 耗。

如果阻抗N 与图2・21中理想变压器的二次侧绕组相连.那么 （2-54） 这个阻抗,当折算到一次侧时,为 Zg 辛二毎二刊厂（善）宝(2-55) 因此，与二次侧绕组相连的阻抗N 折算到一次侧，需将Z ：乘以匝数比的平方X 。

2. 3. 2实际双绕组变压器 1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：汁及绕组电阻：诜心磁导率药为有限值：磁通不完全由铁心构成：讣及诜心有功利无功损耗。

图2-22实际笊相双绕组变乐器的等效电路图 电阻R ］串联于图中一次侧绕氷 用于计及该绕组损耗1饥 电抗天］为一次绕组的漏电抗，串联于一次 绕组用于汁及一次绕组的漏磁通。

实际变压器的等效电路模型普高（杭州）科技开发有限公司 张兴柱 博士实际变压器中的铁芯，其导磁率虽然很高，但并不是无限大，另外由外部电流所产生的磁场也并不能全部分布在铁芯内部，而总会有一小部分分布到铁芯周围的空气中。

所以实际的变压器，其等效电路模型与（1）式所表示的会有一些区别。

s p p s N N i i //=ps p s N N v v //= （1）下面先来看看在漏磁可以忽略，但铁芯导磁率μ为有限这一情况下的变压器等效电路模型。

图1：变压器结构当铁芯的导磁率μ有限时，从图1及磁路KVL 定律可得：s s p p c i N i N R −=Φ故铁芯中的磁通为：）（s s p p ci N i N R −=Φ1 再因为：dt d N v p p Φ= ，dtd N v s s Φ= 所以有：dtL i N N i dt d R N v p mp s p s p c p p m 2di ][=−= （2） sp s p N N v v = （3） 其中：mc p c p mp l A N R N L 22µ==，为变压器原边绕组的电感量，也叫原边的激磁电感。

s ps p mp i N N i i −=，为变压器原边激磁电感中的电流，称为变压器原边的激磁电流。

观察方程（2）和（3），发现在铁芯导磁率有限且忽略漏磁时的变压器等效电路模型，可用图2表示。

由该等效电路可以看出，此时的变压器模型实际上可以看作是由匝比为Np:Ns 的理想变压器（如红色虚线框所示）和原边激磁电感Lmp 并联所成。

图2： 变压器的实际等效电路（1）从图2还可以看出，如果变压器的副边开路，即i s =0，那么变压器的原边就等效为一个激磁电感Lmp ，所以变压器原边的激磁电感可以通过电桥进行测试，测试时只要将变压器的副边开路，在变压器的原边测量其电感就可。

事实上，任何变压器在原边都有一个激磁电感。

在开关电源中，其功率变压器所允许的这个激磁电感大小往往与变换器的拓扑有关，在有些拓扑中（如对称驱动的半桥变换器、全桥变换器），其变压器的激磁电感可以非常大，因而在这些拓扑中的变压器可采用高导磁率的铁芯，而且不用加气隙；在有些拓扑中（如反激变换器、不对称半桥变换器），其变压器的激磁电感不能很大，所以在这些拓扑中的变压器要加上一定的气隙或采用导磁率相对低一些的铁芯。

1.高考中交流电路部分主要考查交变电流的产生和描述、交流电有效值、变压器的规律及动态分析、远距离输电等知识点。

对理想变压器问题应该从电磁感应的本质、电压比、电流比和能量的观点几个方面正确理解。

远距离输电问题应该分段分析，注意各段电压、电流、功率的关系。

掌握输送电过程中功率损失和电压损失。

2.理想变压器和远距离输电问题有时也和电磁感应一起考查，熟练应用法拉第电磁感应定律、楞次定律判断感应电动势、感应电流的方向。

一.理想变压器基本模型（1）理想变压器的构造、作用、原理及特征。

构造：两组线圈（原、副线圈）绕在同一个闭合铁心上构成所谓的变压器。

作用：在办理送电能的过程中改变电压。

原理：其工作原理是利用了电磁感应现象。

特征：正因为是利用电磁感应现象来工作的，所以变压器只能在输送交变电流的电能过程中改变交流电压。

（2）理想变压器的理想化条件及规律如图所示，在理想变压器的原线圈两端加交流电压U 1后，由于电磁感应的原因，原、副线圈中都将产生感应电动势。

根据法拉第电磁感应定律，有∆∆=∆∆=222111,φεφεn t n 忽略原、副线圈内阻，有2211,εε==U U 。

另外，考虑到铁心的导磁作用而且忽略漏磁，即认为任意时刻穿过原、副线圈的磁感线条数都相同，于是又有21φφ∆=∆。

由此便可得理想变压器的电压变化规律为2121n n U U =。

在此基础上再忽略变压器自身的能量损失（一般包括了线圈内能量损失和铁心内能量损失这两部分，分别俗称为“铜损”和“铁损”），有21P P =，而111U I P =，222U I P =。

于是又得理想变压器的电流变化规律为1221n n I I =。

由此可见：①理想变压器的理想化条件一般指的是：忽略原、副线圈内阻上的分压，忽略原、副线圈磁通量的差别，忽略变压器自身的能量损耗（实际上还忽略了变压器原、副线圈电路的功率因素的差别）。

②理想变压器的规律实质上就是法拉第电磁感应定律和能的转化与守恒定律在上述理想化条件下的新的表现形式。

理想变压器等效电路理想变压器等效电路是电学中的一个重要概念，它可以帮助我们更好地理解电路中电压、电流的变化过程。

理想变压器等效电路是由一个理想变压器和一些标准元件（如电阻、电容、电感等）组成的电路模型。

下面，我们将分步骤地阐述理想变压器等效电路。

第一步，了解理想变压器的特点理想变压器是一种绝缘良好、电感大、电阻小、磁路无损耗的变压器。

理想变压器的特点在于，它是一个完全理想化的变压器，没有任何的漏电感和损耗，可以将电能完全传递。

在实际中，变压器的损耗和漏电感是无法避免的，但理想变压器等效电路中可以将变压器所有的损耗和漏电感都归零，只考虑变压器的转化作用。

第二步，建立理想变压器等效电路理想变压器等效电路是由一个理想变压器和一些标准元件组成的电路模型。

根据理想变压器的特点，我们可以将理想变压器等效电路简化为只有两个端子，分别代表输入端和输出端。

同时，电路中还可以加入一些其他元件，如电阻、电容和电感等元件。

这些元件与理想变压器紧密联系，构成了一个完整的电路模型。

通过这个电路模型，我们可以更好地理解理想变压器的工作原理。

第三步，分析理想变压器等效电路的作用理想变压器等效电路的作用在于将电压和电流传递过来，并通过添加其他元件来调节电路的性能。

在理想变压器等效电路中，输入端可以输入一定的电压，而输出端可以输出一个对应的电压。

通过理想变压器等效电路，我们可以调整输入端的电压和输出端的电压以及电流大小。

还可以通过调整其他元件的参数来改变电路的频率响应和波形形状。

第四步，应用理想变压器等效电路理想变压器等效电路广泛应用于电子电路中的各种电源、放大器和信号处理器中。

这些电路需要一个稳定的电压和电流输出，因此理想变压器等效电路可以作为这些电路的重要组成部分。

此外，在建立模拟电路和数字电路的过程中，理想变压器等效电路也经常被用来模拟实际的变压器。

在理想变压器等效电路中，我们可以通过调整电路的参数来改变电路的性能。

但是需要注意的是，在实际电路中，我们无法完全避免损耗和漏电感。

三相变压器等效电阻计算三相变压器的等效电路模型可以简化为一个单相变压器与一个巴肯变压器的组合。

其中，单相变压器的等效电路模型包括主绕组的等效电阻R1，副绕组的等效电阻R2和等效自感L1；巴肯变压器的等效电路模型包括主绕组的等效电阻R'和等效自感L'。

为了计算三相变压器的等效电阻，需要知道以下参数：1.单相变压器的额定电压和额定容量。

2.单相变压器的额定电流和额定电压之间的变比关系。

3.单相变压器的额定电阻和额定自感。

4.形成巴肯变压器的两个单相变压器的等效电阻和等效自感。

计算步骤如下：1.计算单相变压器的等效电阻和等效自感。

单相变压器的等效电阻R1和R2可以根据实际测量值或者通过计算得到。

等效自感L1可以通过实验或者计算得到。

2.计算巴肯变压器的等效电阻和等效自感。

巴肯变压器的等效电阻R'可以通过测量主绕组和副绕组的直流电阻得到。

等效自感L'可以通过实验或者计算得到。

3.计算三相变压器的等效电阻。

对于三相变压器，其等效电路模型可以看作是单相变压器和巴肯变压器的并联连接。

因此，可以将主绕组的等效电阻R1和巴肯变压器的等效电阻R'并联，副绕组的等效电阻R2和巴肯变压器的等效电阻R'并联。

所得到的等效电阻即为三相变压器的等效电阻。

需要注意的是，在实际计算中，还需要考虑变压器的额定容量、变比关系和负载情况等因素。

总结起来，三相变压器的等效电阻计算需要先计算出单相变压器和巴肯变压器的等效电阻和等效自感，然后将其进行相应的组合，得到三相变压器的等效电阻。

计算过程中需要考虑变压器的其他参数，以获得更准确的结果。