变压器的数学模型及等效电路分析方法

基于Matlab电力变压器励磁涌流的分析和仿真
电力变压器励磁涌流分析和仿真是电力系统工程中的重要课题之一。

励磁涌流会导致变压器内部的电流波形畸变，进而引起变压器额定电流的超过。

因此，为了保证变压器的安全运行，必须对励磁涌流进行分析和仿真。

Matlab是一款强大的数学建模和仿真软件，适用于多种工程领域。

基于Matlab进行电力变压器励磁涌流的分析和仿真可以使用以下步骤：
1. 建立变压器模型：根据变压器的参数和拓扑结构，利用Matlab建立变压器的等效电路模型。

可以使用不同的模型，如双绕组模型或多绕組模型。

2. 电源模拟：为了模拟励磁源（如励磁变压器或励磁发电机）的输出，并将其连接到变压器模型的一侧，可以使用Matlab 的函数生成正弦波源。

3. 励磁特性模拟：通过在变压器模型中增加励磁特性模块，可以模拟变压器的磁导特性。

可以使用各种励磁特性模型，如线性励磁模型、饱和励磁模型或非线性励磁模型。

4. 动态仿真：将电源和励磁特性与变压器模型连接，并对整个系统进行动态仿真。

可以使用Matlab的ode45函数或Simulink仿真工具来求解变压器模型的动态方程。

5. 结果分析：根据仿真结果，分析励磁涌流的波形、振幅和频
谱。

可以使用Matlab的绘图功能来绘制变压器电流波形和频
谱图。

基于Matlab进行电力变压器励磁涌流的分析和仿真可以帮助
工程师深入了解励磁涌流的特性，并优化变压器的设计和运行参数。

此外，Matlab还提供了丰富的工具箱和函数，可以用
于更复杂的励磁涌流分析，如短路电流计算、降压启动分析等。

.-电力变压器的参数与数学模型————————————————————————————————作者：————————————————————————————————日期：电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器，假定：绕组电阻为零；因此绕组损耗I2R为零。

铁心磁导率是无穷大，所以铁心磁阻为零。

不计漏磁通；即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:（2-46）磁场强度矢量Hc 为（2-47）其中，磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大，则磁阻R c近似为零。

（2-48）上式可写为：图2-21为双绕组变压器的示意图。

（2-49）或者图2-21中的标记点表示电压E1和E2，在标记点侧是＋极，为同相。

如果图2-21中的其中一个电压极性反向，那么E1与E2相位相差180o。

匝数比k定义如下：理想单相双绕组变压器的基本关系为（2-50）（2-51）由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次侧绕组的复功率为（2-52）代入（2-50）和（2-51）（2-53）可见，流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。

即理想变压器没有有功和无功损耗。

如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连，那么（2-54）这个阻抗，当折算到一次侧时，为（2-55）因此，与二次侧绕组相连的阻抗Z2折算到一次侧，需将Z2乘以匝数比的平方k2。

2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：计及绕组电阻；铁心磁导率为有限值；磁通不完全由铁心构成；计及铁心有功和无功损耗。

图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组，用于计及该绕组损耗I2R。

电抗为一次绕组的漏电抗，串联于一次绕组用于计及一次绕组的漏磁通。

变压器中的等效电阻法
变压器等效电阻公式是R等于PkxUn^2(1000xSn^2)。

将这一等效电阻代替原有的几个电阻后，对于整个电路的电压和电流量不会产生任何的影响。

如果副线圈接的是纯电阻负载Rx，原、副线圈匝数比值（变比n1n2）为n比1，那么该负载在变压器初级表现出来的电阻值为Rx的n的平方倍。

变
变压器等效电阻公式信息
在电力系统稳态里都有，有变压器的数学模型．Un和Sn为额定电压和额定功率．等效阻抗R等于Pk*Un^2(1000*Sn^2)X等于
Uk%*Un^2/(100*Sn)其中Pk变压器短路损耗百分之Uk短路电压百分
比对地导纳G等于P0(1000*Un^2)B等于百分之I0*Sn1设理想变压器原。

副线圈匝数为n1、n2,原副线圈电压为U1、U2,副线圈电阻为R，分析变压器问题，我们总是要把变压器分成左右两个电路来看待，现在我们将右边的电路等效，将其右边的电路等效后消去，变成左边的电路，变成一个单一的回路可以使得问题变得更简单。

变压器中原线圈的等效电阻公式是，R等于K方乘以R总，公式中K是变压比n1n2，R总是副线圈中负载的总电阻。

2.2 变压器的数学模型z变压器正负序参数与等值电路z变压器零序阻抗与等值电路变压器正序参数与等值电路一、变压器的用途与分类z变压器是一种静止电机，将电能从一种电压形式（等级）转换成另一种电压形式（等级）。

z根据用途不同，变压器可以分为：电力变压器与特种变压器。

9电力变压器：在电力系统中传输和分配电能。

9特种变压器：其他用途的变压器，包括电炉变压器、试验变压器（互感器），等。

变压器正序参数与等值电路z根据相数，分为：单相、三相、多相变压器等。

z根据绕组数目，分为：双绕组、自耦、三绕组、多绕组变压器等。

z根据铁心型式，分为：心式、壳式变压器等。

z根据冷却方式，分为：干式、油浸式变压器等。

心式、壳式变压器变压器正序参数与等值电路二、电力变压器的结构z变压器主要部件是绕组和铁心：绕组是变压器的电路，铁心是变压器的磁路，两者构成变压器的核心即电磁部分。

9铁心的型式包括心式(结构简单，工艺简单，应用广泛)和壳式(用在小容量变压器)两种，通常由0.35mm或0.5mm硅钢片叠成。

9绕组用绝缘铜线在绕线模上绕制而成，套装在变压器铁心柱上，为了提高绝缘性能，通常将低压绕组置于在内层，而高压绕组套装在低压绕组外层。

z除了电磁部分，还有油箱、冷却装置、绝缘套管、调压和保护装置等部件。

变压器正序参数与等值电路三、变压器的基本工作原理z 当一次绕组接交流电压后，励磁电流在铁心中产生交变的主磁通Φ。

z Ф在两个绕组中分别产生感应电势e 1和e 2 。

dtd Ne Φ−=11dtd Ne Φ−=22变压器正序参数与等值电路z不计绕组电阻和漏抗压降，则：U1/U2≈ (-e1)/(-e2)=N1/N2=k9k定义为变压器的变比9N2>N1，为升压变压器9N2<N1，为降压变压器四、变压器空载运行z 变压器的一次绕组接交流电源，二次绕组开路，负载电流为零，称为变压器的空载运行。

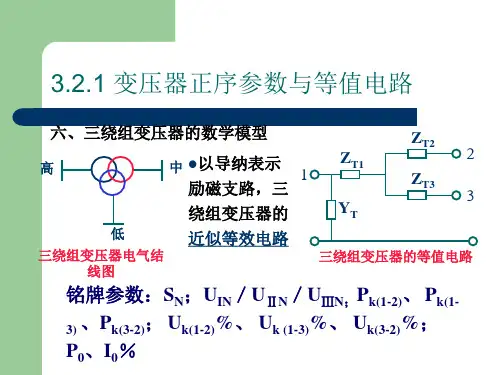
z 一次绕组电流i 0产生励磁磁势F 0= N 1i 09F 0产生的磁通分为两部分:大部分以铁心为磁路，同时与一次绕组N 1和二次绕组N 2匝链，在两个绕组中产生电势e 1和e 2，称为主磁通Ф；另一部分磁通仅与一次绕组匝链，通过油或空气形成闭路，称为一次绕组的漏磁通Ф1σ变压器正序参数与等值电路变压器正序参数与等值电路z一次绕组电流i 0分为两部分，i μ和i Fe ：i μ用于激励主磁通，称为磁化电流，与电势e 1之间的相位差是90°，是无功电流；i Fe 与铁心损耗相对应，与-e 1同相位，是有功电流9i 0即是励磁电流9X m 反映了变压器铁心的导磁性能，代表了主磁通Φ对电路的电磁效应，称为励磁电抗；R m 是用来代表铁耗的等效电阻，称为励磁电阻。

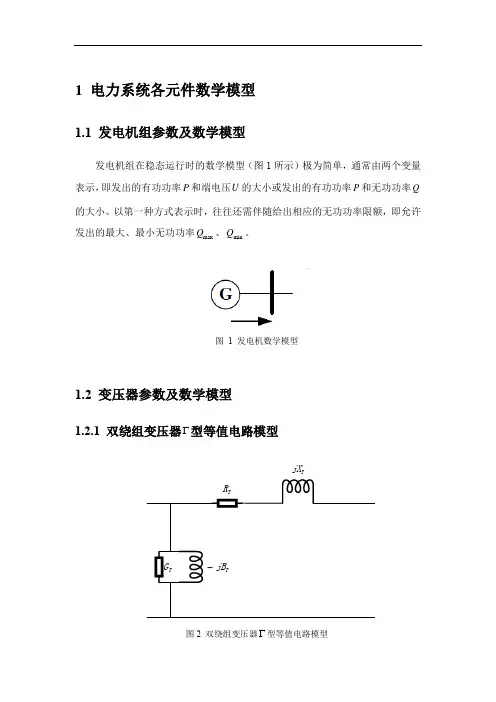
1 电力系统各元件数学模型1.1 发电机组参数及数学模型发电机组在稳态运行时的数学模型（图1所示）极为简单，通常由两个变量表示，即发出的有功功率P 和端电压U 的大小或发出的有功功率P 和无功功率Q 的大小。

以第一种方式表示时，往往还需伴随给出相应的无功功率限额，即允许发出的最大、最小无功功率max Q 、min Q 。

图 1 发电机数学模型1.2 变压器参数及数学模型1.2.1双绕组变压器Γ型等值电路模型TjX 图2 双绕组变压器Γ型等值电路模型双绕组变压器Γ型等值电路模型如图2所示，电路参数通过以下公式计算。

注意，公式中N U 取不同绕组的额定电压，表示将参数归算到相应绕组所在的电压等级（所得所得阻抗/导纳参数都是等值为Y/Y 接线的单相参数）;公式中各参数由变压器厂家提供，采用实用单位。

22020210001001000%100k N T Nk NT N T NN T N P U R S U U X S P G U I S B U ⎧∙=⎪⎪⎪%∙=⎪⎪⎨⎪=⎪⎪⎪=∙⎪⎩（1-1） 其中，k P 为短路损耗，k U %为短路电压百分数，0P 为空载损耗，0%I 为空载电流百分数，N U 为归算侧的额定电压，N S 为额定容量 该电路模型一般用于手算潮流中。

1.2.2 双绕组变压器T 型等值电路模型1jX '图 3 双绕组变压器T 型等值电路模型其中，1R 和1X 为绕组1的电阻和漏抗，'2R ，'2X 为归算到1次侧的绕组2 的电阻和漏抗，m R 和m X 为励磁支路的电阻和电抗。

该电路模型一般用于电机学中加深对一二次侧和励磁支路电阻电抗的理解以及手算潮流计算中。

1.2.2 三绕组变压器Z 图4三绕组变压器的等值电路三绕组变压器的等值电路如图3所示，图中，变压器的励磁支路也以导纳表示。

该电路模型一般用于手算潮流计算中。

三绕组变压器的参数计算如下： 电阻：由短路损耗计算()()()1(12)(31)(23)2(23)(12)(31)3(31)(23)(12)121212k k k k k k k k k P P P P P P P P P P P P ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩（1-2） 211222233100010001000k N T Nk N T Nk NT N P U R S P U R S P U R S ⎧∙=⎪⎪⎪∙⎪=⎨⎪⎪∙⎪=⎪⎩（1-3） 其中，k P 为短路损耗，N U 为归算侧的额定电压，N S 为额定容量对于容量比为100/100/50和100/50/100的变压器，厂家提供的短路损耗是小容量绕组达到自身额定电流()/2N I 时的试验数据，计算时应首先将短路损耗折算为对应于变压器额定电流()N I 的值例如，对于100/100/50型变压器，厂家提供的是未经折算的短路损耗'(23)k P -，'(31)k P -，'(12)k P -首先应进行容量归算'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩（1-4） 按新标准，厂家仅提供最大短路损耗max k P ，按以下公式计算电阻：2max (100%)2(50%)(100%)20002k N T N T T P U R S RR ⎧=⎪⎨⎪=⎩（1-5） 其中max k P 为最大短路损耗，N U 为归算侧的额定电压，N S 为额定容量 电抗：由短路电压百分数计算()()()1(12)(31)(23)2(12)(23)(31)3(23)(31)(12)1%%%%21%%%%21%%%%2k k k k k k k k k k k k U U U U U U U U U U U U ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩（1-6） 211222233100100100k N T Nk N T N k NT N U U X S U U X S U U X S ⎧%=⎪⎪⎪%⎪=⎨⎪⎪%⎪=⎪⎩（1-7） 其中，k U %为短路电压百分数，N U 为归算侧的额定电压，N S 为额定容量 注意，厂家提供的短路电压是经过额定电流折算后的数据。

变压器等效电路获取的教学方法谢宝昌【摘要】变压器是典型的电磁耦合器件,其等效电路获取是教学的重点内容.传统方法是基于变压器内部电磁关系和绕组折算获得T型等效电路,本文提出了一种新的获取等效电路的教学方法.笔者先通过物理过程分析获取电路和磁路耦合模型,然后通过深入分析磁路中磁通、磁势和磁导关系并引入相关电流分量,逐步用无源电路元件等效替代漏电势源和激磁电流源,而完全电磁耦合部分则用理想变压器替代,最后利用理想变压器的变换特性获得T型等效电路.教学分析过程概念明确又结合学生本身具有的电路和磁路基础知识,在此基础上再分析绕组折算原理可以起到事半功倍的教学效果.【期刊名称】《电气电子教学学报》【年(卷),期】2013(035)002【总页数】3页(P60-62)【关键词】变压器;等效电路;电磁耦合模型;磁化源【作者】谢宝昌【作者单位】上海交通大学电子信息与电气工程学院,上海200240【正文语种】中文【中图分类】TM401变压器是“电机学”的重要内容之一。

对变压器等效电路获取方法的认识有助于正确理解变压器基本原理，也有助于交流感应电机的教学。

传统的获取方法是基于变压器内部电磁关系和绕组折算原理获得 T 型等效电路［1，2］，学生往往不能理解绕组折算思想而使教学效果大打折扣。

本文提出了一种新的获取等效电路的教学方法，先通过物理过程分析获取电路和磁路耦合模型，然后通过深入分析漏磁路和主磁路中磁通、磁势和磁导关系并引入主磁路铁耗电流分量和磁化电流分量，逐步用电路元件等效替代漏电势源和激磁电流源，而完全电磁耦合部分则用理想变压器替代，最后利用理想变压器的变换特性获得T型等效电路。

1 变压器的物理模型本文以双绕组变压器为例阐述其等效电路获取的教学过程，该过程也适用于其它类型变压器。

为了让学生理解等效电路获取过程，首先必须解释清楚物理模型，包括参考方向的确定和内部电磁耦合过程。

双绕组变压器的参考方向是这样确定的:按照电动机惯例规定端口电压与电流，即电能输入变压器，内部绕组电流与磁场满足右手螺旋关系，磁场与感应电势也满足右手螺旋关系，根据一次侧和二次侧绕组绕向，所有物理量的正方向如图1所示。

理想变压器的综合分析理想变压器是电能转换系统中最常用的装置之一。

它通常用于变压、隔离、耦合和功率匹配等应用领域。

理想变压器是一种没有漏抗的模型，其次级侧输出电压与次级施加电压的比值等于它们的匝数比。

理想变压器的原理是基于强磁耦合的电感耦合，通过其交流电磁感应，实现了电压和电流的转换。

理想变压器是在没有能量损失，同时维持磁通连续性的前提下工作的。

因此，它的电流和电压比是完全由匝数比所决定的。

理想变压器的数学模型中，假设两组绕组之间没有漏抗，这意味着所有的磁通都集中于铁心之间。

理想变压器的线圈是不耗散的，没有电阻和电感，因此没有能量损失。

这样，它的工作效率就达到了100%。

理想变压器的性能指标可以通过以下参数来描述：1. 匝数比：变压器的主要功能是转换电压。

匝数比是理想变压器中二者之间相当于给定电压比的表达式。

它为Np/NS （次级匝数÷主级匝数）。

2. 变压度：变压器的工作是在输入和输出侧之间建立电压比。

而变压度是转换器中输入和输出电压的比值。

因此，它是来自绕组的电压比的表征，为VP/VS（输入电压÷输出电压）。

3. 社会电抗率：社会电抗率是描述理想变压器在未激磁情况下的漏磁阻抗的一个术语。

它可以通过复数表达式1/jωL 来描述，其中L为漏感。

理想变压器的分析过程中，需要通过对分压器，分流器和等效电路的分析来确定其性能。

在分析过程中，我们可以将变压器想象成一个含有内部阻抗的电源，是由主线圈的响应直接推导出来的。

由于内部耗散元件的消耗，则需要计算戴入主线圈的热功率。

这种功率损失随着线圈的制造质量和使用条件的影响而发生变化。

需要注意的是，在现实世界中，理想变压器并不存在。

所有变压器都会存在漏抗和铁损耗。

因此，在实际应用中，通常需要考虑压降和损耗等因素。

未考虑损耗时，理想变压器的特征与实际变压器的特征相同，除了在变压器的事实性处理等方面存在差异。

总的来说，理想变压器是在没有能量损失和维持磁通连续性的前提下工作的。

.-电力变压器的参数与数学模型————————————————————————————————作者：————————————————————————————————日期：电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器，假定：绕组电阻为零；因此绕组损耗I2R为零。

铁心磁导率是无穷大，所以铁心磁阻为零。

不计漏磁通；即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。

不计铁心损耗。

图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:（2-46）磁场强度矢量Hc 为（2-47）其中，磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大，则磁阻R c近似为零。

（2-48）上式可写为：图2-21为双绕组变压器的示意图。

（2-49）或者图2-21中的标记点表示电压E1和E2，在标记点侧是＋极，为同相。

如果图2-21中的其中一个电压极性反向，那么E1与E2相位相差180o。

匝数比k定义如下：理想单相双绕组变压器的基本关系为（2-50）（2-51）由推导可得两个关于复功率和阻抗的关系如下。

图2-21中流进一次侧绕组的复功率为（2-52）代入（2-50）和（2-51）（2-53）可见，流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。

即理想变压器没有有功和无功损耗。

如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连，那么（2-54）这个阻抗，当折算到一次侧时，为（2-55）因此，与二次侧绕组相连的阻抗Z2折算到一次侧，需将Z2乘以匝数比的平方k2。

2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器，与理想变压器的区别如下：计及绕组电阻；铁心磁导率为有限值；磁通不完全由铁心构成；计及铁心有功和无功损耗。

图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组，用于计及该绕组损耗I2R。

电抗为一次绕组的漏电抗，串联于一次绕组用于计及一次绕组的漏磁通。

计及边端效应的直线式移相变压器等效电路分析
赵镜红;周长朵;王涵铭;严思念;严冬傲
【期刊名称】《电工技术学报》
【年(卷),期】2024(39)6
【摘要】直线式移相变压器是一种新型移相变压器,具有绕组结构简单、易于模块化和可任意角度移相的优点。

其直线型结构导致变压器存在边端效应,进而导致气隙磁场产生畸变。

为了计算出边端效应产生的影响,该文从直线式移相变压器的磁场进行深入分析,并建立计及边端效应的等效电路模型。

首先,基于一维场理论对直线式移相变压器进行数学分析,根据场路复功率相等的原则,推导出等效电路二次侧参数,并计算出边端效应修正系数;然后,根据边端效应的分析结果和直线感应电机的等效电路拓扑建立计及边端效应的等效电路模型;最后,通过直线式移相变压器的二维有限元仿真模型和小功率样机的实验,验证了建模方法的合理性和等效电路模型的准确性。

【总页数】14页(P1792-1805)
【作者】赵镜红;周长朵;王涵铭;严思念;严冬傲
【作者单位】海军工程大学电气工程学院
【正文语种】中文
【中图分类】TM401
【相关文献】
1.直线式移相变压器边端效应研究
2.用等效电路分析动圈式弧焊变压器的方法
3.直线式移相变压器两类纵向边端效应分析
4.12/3相直线式移相变压器设计
5.移相式相序检测电路分析
因版权原因，仅展示原文概要，查看原文内容请购买。