质心参考系

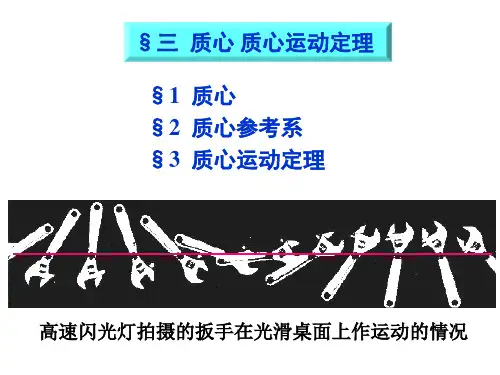
质心系前面我们回顾了Newton 定律以及由它导出的一些重要的推论，主要有由于Newton 定律只在惯性系中才是成立的，因此作为其推论，这些定理的成立的前提当然也要求所涉及的量都是相对于某个惯性系测量或计算出的。

但是，存在一个可能是非惯性系的特殊参考系，这些推论在其中也都是成立的，其中一些，譬如动量定理，其形式来的还要更加简单。

这个特殊的参考系就是质心系，也就是以质心为原点并随质心一起平动的参考系。

如果我们用表示粒子在某个惯性系中的位矢，而a r K a a r ′K 则表示它在质心系中的位矢，它们之间有如下关系：CM a r R r a ′=+K K K (1) 在质心系中质心当然始终是位于原点的，因此0a a am r ′=∑K (2)另一方面，体系的总动量就是质心的动量，因此，体系在质心系中的总动量就该为零。

当然，上式两边对时间求微商也就得到了同样的结论。

， 0a a a a a ad p m r m r dt ′′==∑∑K K ′=K (3) 这个方程其地位就相当于在一般惯性系中的质心运动定理。

利用这些关系，你会发现描述体系状态的那些量——如角动量以及动能——都可以表示为两部分之和：一部分描述质心的运动，另一部分则描述体系相对于质心的运动。

如角动量()()CM CM CM CM CM a a a a a a a a a a a aa a a a a L L r p R r m R r R m R r m r R m r a′′==×=+×+⎛⎞′′=×+×⎜⎟⎝⎠′+×∑∑∑∑∑∑K K K K K K K K K K K K K K a a a m r ′+∑K CM R ⎛⎞×⎜⎟⎜⎟⎝⎠K (4) 其中第一项正是质心的角动量，而最后一项则是体系相对于质心的角动量： CM CM CM , a a aL R P L r m ar ′′=×=×′∑K K K K K K (5) 而中间两项则显然是等于零的，因此CM L L L ′=+K K K (6) 角动量变化的原因，即力矩，也可以作类似的分解，一部分对质心的运动负责，另一部分则负责相对于质心的运动：()CM CM CM CM CM with and a a a a a a a a a a aa a a aa r F R r F R F r F R F r F ττττττ′==×=+×′=×+×′′=+=×=×∑∑∑∑∑∑K K K K KK K K K K K ′K K K K K K K K (7)由于总的外力，第一项正是质心角动量的变化率，而我们又知道CMF MP =K K Lτ=K K ，由此L τ′′=K K (8) 即不管质心系是否是惯性参考系（也就是说，不管体系是否受到外力的作用），在质心系中角动量定理依然成立。

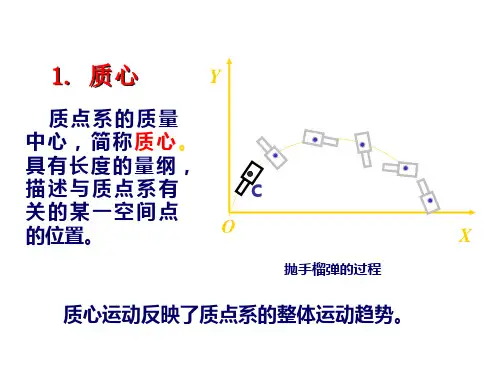
太阳系质心天球坐标系-概述说明以及解释1.引言1.1 概述太阳系质心天球坐标系是一种重要的天文坐标系，用于描述太阳系中天体的运动和位置。

在这个坐标系中，太阳系的质心被视为参考点，其他天体相对于太阳系质心的位置被测量和描述。

太阳系质心天球坐标系的定义有助于研究太阳系内部天体之间的相对运动以及太阳系与其他恒星或星系的相对位置。

太阳系质心是太阳系中所有天体的质量中心，包括太阳、行星、卫星和小行星等。

太阳系质心并不在太阳的中心，而是在太阳与其他天体间的引力作用下产生的一个点。

这个质心不仅受到太阳和其他天体的引力影响，还受到其他星系和大质量天体的引力影响。

因此，确定太阳系质心的位置对于研究太阳系动力学和天体运动的影响非常重要。

天球坐标系是一种球坐标系，用于描述天体在天球上的位置。

在天球坐标系中，太阳系质心被定义为原点，而赤道是一个关键的参考面。

天球坐标系的两个基本坐标是赤经和赤纬，分别表示天体在天球上的经度和纬度。

这种坐标系使得天体的观测和测量可以更加方便和准确。

太阳系质心天球坐标系的重要性在于它提供了一个标准的参考框架，使得天文学家和研究者能够更好地理解太阳系中天体的运动和相对位置。

通过观测和测量太阳系中的天体在这个坐标系下的位置，我们可以推断出它们的轨道、运动速度和相互作用等重要信息。

此外，太阳系质心天球坐标系还与其他星系和宇宙中的天体位置相联系，有助于研究天体的演化、星系的相对位置以及宇宙的大尺度结构等问题。

综上所述，太阳系质心天球坐标系是一个重要且必要的工具，用于研究和描述太阳系中天体的运动与位置。

它为我们提供了一个标准的参考框架，使得我们能够更好地了解太阳系内部以及与其他星系和宇宙之间的关系。

通过进一步研究太阳系质心天球坐标系，我们可以对太阳系的演化和宇宙的结构有更深入的认识。

1.2文章结构1.2 文章结构本文将分为三个主要部分来讨论太阳系质心天球坐标系。

首先，在引言部分概述太阳系质心天球坐标系的重要性和目的。

质点系和质心系是在物体运动和动力学研究中用来描述和分析多个质点的参考系统。

它们的区别在于坐标系的选择和描述对象的方式。

1. 质点系：质点系是指由多个质点组成的系统。

在质点系中，每一个质点被看作没有大小和形状的质点，只有质量和位置。

质点系的运动可以通过描述每个质点的位置、速度和加速度来表示。

对于质点系的研究，可以选取任意一个坐标系进行描述，通常常用惯性坐标系或者其他方便的参考系。

2. 质心系：质心系是以质点系的质心为原点，以质心系的速度作为参考系的坐标系。

质心是质点系的所有质点质量的加权平均位置，通过对质点系中的质点质量进行求和，并根据其位置和质量加权平均得出。

质心系的选择有助于简化质点系的运动描述，特别是在分析质点系的整体运动和动力学性质时。

在质心系中，质点系的总动量为零，从而简化了动力学方程的形式。

总结起来，质点系是由多个质点组成的系统，可以选择任意坐标系进行描述；而质心系是以质点系的质心为原点的坐标系，通过简化质点系的运动描述来分析质点系的整体运动和动力学性质。

质心系的选择可以使动力学方程的形式更加简
化。

质心参考系在力学教学中的重要性研究作者：霍海波范其丽来源：《经营管理者·上旬刊》2016年第04期摘要：在应用物理专业的教学过程中，有的知识点具有连续应用的特点，而这些知识点在定义时如果学生没能很好的掌握，结果就会导致在后续的学习过程中再遇到该类问题时，由于概念及定义掌握不牢固、印象不深，而出现理解上的问题。

久而久之，必定影响学生的学习积极性。

在力学的教学过程中，质心参考系就是这样一个连续应用的例子。

本文给出了质心参考系的定义，并总结了在力学及量子力学中质心参考系的连续应用，通过举例加深理解，以使学生能够很好的掌握关于质心参考系的定义，并能熟练应用。

关键词：质心参考系应用一、质心参考系的定义及相关定理力学是物理专业学生接触的第一门专业课，它有区别于中学物理中的力学，需要用矢量和微积分来处理问题，需要转变分析方法，同时也是后续课程学习的专业基础课，对物理专业的学生来说，地位十分重要。

在力学教学过程中，很多同学由于新接触一些物理概念，理解上会出现困难，结果此概念在后续章节的学习过程中持续出现，导致部分同学理解连续出现问题，影响学习积极性。

如质心参考系就是其中一个在力学教学中连续应用的概念。

由于质心参考系在力学学习中的重要性，在此首先给出质心和质心参考系的定义。

质心参考系示意图如图1所示图1 质心参考系示意图其中o～xyz为惯性参考系，o’～x'y'z’是以质心为坐标原点的质心参考系，设质点组中第i 个质点的质量为，相对于质心C的位矢为，质心坐标定义如下上式所确定的空间点和质点系密切相关，叫做质点系的质量中心，简称质心。

和XC，YC，ZC分别称为质心的位置矢量和质心坐标，它实际上是质点系质量分布的平均坐标。

如果为联系分布的刚体，则上式得求和符号变为积分。

在分析一些问题时，采用质心坐标系可以使问题简化，质心坐标系就是将坐标系变为o’～x'y'z’，一个显著特点是质心在质心坐标系中的位置矢量为零，根据这一特点，质心坐标系具有以下一些特性1.质点系质心运动定理即质点系总质量与质心加速度的乘积总是等于质点系所受外力的矢量和，这一点在我们分析力作用在物体不同位置时产生的复杂运动形式尤为重要，通过分析这些力的矢量和可以确定质心的运动状态，进而使问题简化。

知识创造未来
质心参考系
质心参考系是在物理学中用于研究多体问题的一种参考系。

在质心
参考系中，观察者位于多个物体的质心位置，这样可以简化问题的
分析和计算。

质心是指多个物体的质量加权平均位置，也可以看作是多个物体所
在位置的中心。

在质心参考系中，质心位置被定义为原点，其他物
体相对于质心的位置可以视为相对位置。

在质心参考系中，考虑不
同物体之间的相对位置和质心到物体的运动即可。

质心参考系的一个重要特点是，质心保持静止或者以恒定速度运动，因为质心的位置是由物体的质量和位置加权平均得到的。

这使得分
析多体问题变得简单，可以将问题简化为质心的运动和物体相对质
心的运动。

质心参考系在多体动力学和静力学中都有广泛应用。

通过使用质心
参考系，可以减少计算量并简化问题的分析，从而更容易理解和解
决多体问题。

1。

理论力学知识点总结联系一、牛顿运动定律1.牛顿第一定律：一个静止的物体如果不受力的作用，将永远保持静止；一个匀速直线运动的物体如果不受力的作用，将永远保持匀速运动。

牛顿第一定律是描述惯性的物理定律。

它告诉我们，如果物体不受外力作用，它将永远保持原来的状态，包括静止和匀速直线运动状态。

这意味着，物体本身具有一种保持状态的倾向，这种倾向就是物体的惯性。

牛顿第一定律为我们分析物体运动提供了重要的参考。

2.牛顿第二定律：物体受到的作用力等于其质量乘以加速度。

牛顿第二定律是最著名的力学定律之一，它描述了物体所受力和物体的加速度之间的关系。

表达式为F=ma，其中F为受到的作用力，m为物体的质量，a为物体的加速度。

牛顿第二定律告诉我们，作用力越大，加速度越大；质量越大，同样的力的作用下加速度越小。

这一定律为我们提供了分析物体受力和加速度的重要工具。

3.牛顿第三定律：相互作用的两个物体对彼此的作用力大小相等、方向相反。

牛顿第三定律描述了物体间相互作用的性质。

它告诉我们，相互作用的两个物体对彼此的作用力大小相等、方向相反。

这一定律为我们提供了理解物体相互作用的重要原则。

二、动量定理和动能定理1.动量定理：物体的动量变化率等于它所受到的外力。

动量定理描述了物体的动量随时间的变化规律。

它告诉我们，物体的动量变化率等于它所受到的外力。

表达式为F=dp/dt，其中F为外力，p为物体的动量，t为时间。

动量定理为我们提供了一种描述物体受力和动量变化的重要方法。

2.动能定理：物体的动能变化率等于它所受到的外力与物体的速度之积。

动能定理描述了物体的动能随时间的变化规律。

它告诉我们，物体的动能变化率等于它所受到的外力与物体的速度之积。

表达式为Fv=d(1/2 mv^2)/dt，其中F为外力，v为物体的速度，m为物体的质量。

动能定理为我们提供了一种描述物体受力和动能变化的重要方法。

三、角动量定理和万有引力定律1.角动量定理：物体的角动量变化率等于外力对物体的力矩。