08-质心系

质心系前面我们回顾了Newton 定律以及由它导出的一些重要的推论，主要有由于Newton 定律只在惯性系中才是成立的，因此作为其推论，这些定理的成立的前提当然也要求所涉及的量都是相对于某个惯性系测量或计算出的。

但是，存在一个可能是非惯性系的特殊参考系，这些推论在其中也都是成立的，其中一些，譬如动量定理，其形式来的还要更加简单。

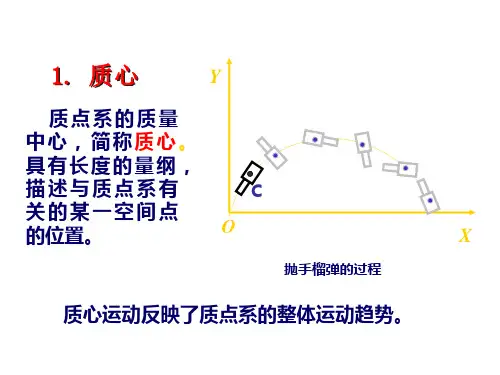
这个特殊的参考系就是质心系，也就是以质心为原点并随质心一起平动的参考系。

如果我们用表示粒子在某个惯性系中的位矢，而a r K a a r ′K 则表示它在质心系中的位矢，它们之间有如下关系：CM a r R r a ′=+K K K (1) 在质心系中质心当然始终是位于原点的，因此0a a am r ′=∑K (2)另一方面，体系的总动量就是质心的动量，因此，体系在质心系中的总动量就该为零。

当然，上式两边对时间求微商也就得到了同样的结论。

， 0a a a a a ad p m r m r dt ′′==∑∑K K ′=K (3) 这个方程其地位就相当于在一般惯性系中的质心运动定理。

利用这些关系，你会发现描述体系状态的那些量——如角动量以及动能——都可以表示为两部分之和：一部分描述质心的运动，另一部分则描述体系相对于质心的运动。

如角动量()()CM CM CM CM CM a a a a a a a a a a a aa a a a a L L r p R r m R r R m R r m r R m r a′′==×=+×+⎛⎞′′=×+×⎜⎟⎝⎠′+×∑∑∑∑∑∑K K K K K K K K K K K K K K a a a m r ′+∑K CM R ⎛⎞×⎜⎟⎜⎟⎝⎠K (4) 其中第一项正是质心的角动量，而最后一项则是体系相对于质心的角动量： CM CM CM , a a aL R P L r m ar ′′=×=×′∑K K K K K K (5) 而中间两项则显然是等于零的，因此CM L L L ′=+K K K (6) 角动量变化的原因，即力矩，也可以作类似的分解，一部分对质心的运动负责，另一部分则负责相对于质心的运动：()CM CM CM CM CM with and a a a a a a a a a a aa a a aa r F R r F R F r F R F r F ττττττ′==×=+×′=×+×′′=+=×=×∑∑∑∑∑∑K K K K KK K K K K K ′K K K K K K K K (7)由于总的外力，第一项正是质心角动量的变化率，而我们又知道CMF MP =K K Lτ=K K ，由此L τ′′=K K (8) 即不管质心系是否是惯性参考系（也就是说，不管体系是否受到外力的作用），在质心系中角动量定理依然成立。

质心系中质点组的运动定律宁国强1. 引言众所周知，牛顿运动定律是在惯性系中低速情况下才成立的规律。

所以，以牛顿运动定律为基础而推导出来的一些运动定律当然也都只能在惯性系中才成立[1~4]。

在研究和解决力学问题时通常选用惯性参考系，但在许多情况下选用非惯性参考系可能会使问题简单化[5~8]。

在非惯性系中引入惯性力以后，牛顿运动定律可以沿用，但其推导出的运动定律是否可以沿用呢？如果可以沿用，其表达式又如何呢？本文将导出质心坐标系（质心坐标系既可以是惯性系，也可以是非惯性系）中质点组的运动定律，并以此为基础讨论质心坐标系中的碰撞与散射现象。

2. 质心参考系以质点组的质心为原点，坐标轴与静止惯性参考系平行，这种参考系称为质心参考系或质心系。

根据质心和质心参考系的定义，可以知道质心参考系的特征。

由质心定义可知，在质心参考系中，质心的位置矢量为0='='∑∑ii i c m r m r. （2-1）将c r '对时间取一阶导数，得0i i c im v v m ''==∑∑. (2-2) 由上式知0i i m v '=∑. (2-3)公式（2—3）说明了质点组对质心的总动量为零，这个结论是质心参考系定义的直接结果，与质点组整个系统的运动无关系，它反映出了质心参考系的特征。

因此，我们称质心参考系为零动量参考系。

正是由于有了这一特征，才能使得质心参考系成为讨论质点组运动的重要参考系[9~11]。

质心参考系既可以是惯性系，也可以是非惯性系。

由质心运动定理 ∑==dtv d m r m F cci 可知，我们所研究的系统，如果所受的合外力为零，则质心C 在静止惯性参考系中以恒定速度c V作惯性运动，此时质心参考系也是惯性参考系。

如果所受合外力不为零，则质心相对于静止惯性系作加速运动，这样，质心参考系就不再是惯性参考系，而是非惯性参考系。

3. 质心系中质点组的运动定律3.1 质心系中质点组的动量定理和动量守恒定律若在非惯性系中引入惯性力，则可以导出适用于非惯性系的动量定理，推导如下：设有一质心系C x y z '''-(以下简称k '系)相对另一惯性系O xyz -（以下简称k 系）作加速运动，k '系原点在k 系中的加速度用c a 表示，现有n 个质点组成的质点系相对k 系作加速运动，n r r r ''',,,21表示各质点相对k '系原点的位矢，n v v v ''',,,21表示各质点相对于k '系运动的速度。

质点系质心位置守恒的条件
质点系质心位置守恒的条件是基于动量守恒定律和质心定义的。

根据动量守恒定律，当质点系内部无外力作用时，系统的总动量守恒。

而质心是质点系统的一种特殊位置，它可以视为质点系的平均位置，具有使得系统动量守恒的特性。

根据质心的定义，质点系质心的位置可以通过质点的质量和位置的加权平均来计算。

具体地说，如果质点系由N个质点组成，其中第i个质点的质量为mi，位于坐标(xi, yi, zi)，则质心的位置可以通过以下公式计算：
X = (m1x1 + m2x2 + ... + mN xN) / (m1 + m2 + ... + mN)
Y = (m1y1 + m2y2 + ... + mN yN) / (m1 + m2 + ... + mN)
Z = (m1z1 + m2z2 + ... + mN zN) / (m1 + m2 + ... + mN)
X、Y和Z分别表示质心在x、y和z坐标轴上的位置。

由于质心的位置是通过加权平均计算得出的，质心的位置不仅依赖于质点们的位置，还与各个质点的质量相关。

当质点系内部无外力作用时，如果不出现质点的质量发生改变的情况，质心的位置应保持不变。

质点系质心位置守恒的条件是质点系内部无外力作用，并且质点的质量不发生改变。

质心与质点系的机械能守恒在物理学中，质心与质点系的机械能守恒是一个重要的概念。

质心是一个系统中所有质点的平均位置，而质点系则是由多个质点组成的系统。

在理论力学中，质心与质点系的机械能守恒定律指出，一个质点系的机械能在没有外力做功的情况下保持不变。

首先，我们来了解一下质心与质点系的概念。

质心是一个系统中所有质点的质量加权平均位置。

对于一个由N个质点组成的质点系，其质心的位置可以通过下列公式计算得出：X_cm = (m₁x₁ + m₂x₂ + … + mₙxₙ) / (m₁ + m₂ + … + mₙ)其中，X_cm是质心的位置，m₁、m₂等表示各个质点的质量，x₁、x₂等表示各个质点的位置。

质心的概念对于分析系统的整体运动非常有用。

当我们研究质点系的机械能守恒时，可以将系统的运动简化为质心的运动和质点系相对质心的运动。

接下来，我们来探讨质心与质点系的机械能守恒。

根据力学的基本原理，质点系的机械能守恒要求系统中的外力做功为零。

这意味着质心和质点系相对质心的动能和势能的总和保持不变。

质心的动能可以通过下列公式计算得出：K_cm = 1/2 M V_cm²其中，M表示质点系的总质量，V_cm表示质心的速度。

质点系相对质心的动能可以通过下列公式计算得出：K_r = 1/2 Σ(mᵢ vᵢ)²其中，mᵢ、vᵢ分别表示质点系中各个质点的质量和速度。

系统中的势能可以表示为：U = ΣUᵢ其中，Uᵢ表示各个质点的势能。

根据机械能守恒定律，当系统中没有外力做功时，质心和质点系相对质心的动能和势能的总和保持不变：K_cm + K_r + U = 常数这意味着当质心的动能增加或减少时，质点系相对质心的动能和势能将发生相应的变化，以保证机械能守恒。

值得注意的是，机械能守恒定律只适用于没有外力做功的情况。

如果有外力对系统做功，机械能将不再守恒。

质心与质点系的机械能守恒定律在实际生活中有着广泛的应用。

例如，当一个体育器材运动员从旋转状态中脱离时，他们通常会利用质心和质点系相对质心的机械能守恒来实现动作的平稳转变。