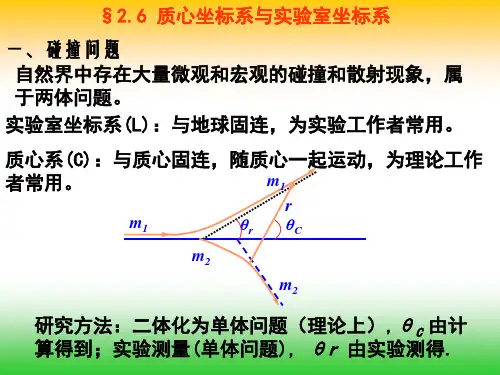
(8)质心系

质心系前面我们回顾了Newton 定律以及由它导出的一些重要的推论，主要有由于Newton 定律只在惯性系中才是成立的，因此作为其推论，这些定理的成立的前提当然也要求所涉及的量都是相对于某个惯性系测量或计算出的。

但是，存在一个可能是非惯性系的特殊参考系，这些推论在其中也都是成立的，其中一些，譬如动量定理，其形式来的还要更加简单。

这个特殊的参考系就是质心系，也就是以质心为原点并随质心一起平动的参考系。

如果我们用表示粒子在某个惯性系中的位矢，而a r K a a r ′K 则表示它在质心系中的位矢，它们之间有如下关系：CM a r R r a ′=+K K K (1) 在质心系中质心当然始终是位于原点的，因此0a a am r ′=∑K (2)另一方面，体系的总动量就是质心的动量，因此，体系在质心系中的总动量就该为零。

当然，上式两边对时间求微商也就得到了同样的结论。

， 0a a a a a ad p m r m r dt ′′==∑∑K K ′=K (3) 这个方程其地位就相当于在一般惯性系中的质心运动定理。

利用这些关系，你会发现描述体系状态的那些量——如角动量以及动能——都可以表示为两部分之和：一部分描述质心的运动，另一部分则描述体系相对于质心的运动。

如角动量()()CM CM CM CM CM a a a a a a a a a a a aa a a a a L L r p R r m R r R m R r m r R m r a′′==×=+×+⎛⎞′′=×+×⎜⎟⎝⎠′+×∑∑∑∑∑∑K K K K K K K K K K K K K K a a a m r ′+∑K CM R ⎛⎞×⎜⎟⎜⎟⎝⎠K (4) 其中第一项正是质心的角动量，而最后一项则是体系相对于质心的角动量： CM CM CM , a a aL R P L r m ar ′′=×=×′∑K K K K K K (5) 而中间两项则显然是等于零的，因此CM L L L ′=+K K K (6) 角动量变化的原因，即力矩，也可以作类似的分解，一部分对质心的运动负责，另一部分则负责相对于质心的运动：()CM CM CM CM CM with and a a a a a a a a a a aa a a aa r F R r F R F r F R F r F ττττττ′==×=+×′=×+×′′=+=×=×∑∑∑∑∑∑K K K K KK K K K K K ′K K K K K K K K (7)由于总的外力，第一项正是质心角动量的变化率，而我们又知道CMF MP =K K Lτ=K K ，由此L τ′′=K K (8) 即不管质心系是否是惯性参考系（也就是说，不管体系是否受到外力的作用），在质心系中角动量定理依然成立。

例谈质心和质心系在解题中的应用陈新学(杭州学军中学教育集团文渊中学ꎬ浙江杭州３１１２００)摘㊀要:文章从质心的概念出发ꎬ推导质心运动定理ꎬ阐述质心参考系ꎬ探讨应用质心相关知识解题注意的问题.关键词:质心ꎻ质心运动定理ꎻ质心系ꎻ物理竞赛中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２３)１９－０１２３－０３收稿日期:２０２３－０４－０５作者简介:陈新学(１９７８.１１－)ꎬ男ꎬ安徽省休宁人ꎬ硕士ꎬ中学一级教师ꎬ从事高中物理教学研究.㊀㊀质心是力学的一个重要概念ꎬ一些看似复杂的力学问题ꎬ如果应用质心的相关知识分析ꎬ解题思路会变得清晰ꎬ解题过程会变得简单.本文借助于几个典型问题探讨质心的概念㊁质心运动定理以及质心参考系在解题中的应用.１质心的相关概念１.１质心和质心运动定理设Ｎ个质点组成的系统(简称质点系或系统)中ꎬ各质点的位置矢量(简称位矢)分别为ｒ１ꎬｒ２ꎬ ꎬｒＮꎬ定义此质点系的质心的位矢ｒ⇀Ｃ＝ｍ１ｒ⇀１＋ｍ２ｒ⇀２＋ ＋ｍＮｒ⇀Ｎｍ１＋ｍ２＋ ＋ｍＮ＝ðＮｉ＝１ｍｉｒ⇀ｉðＮｉ＝１ｍｉ＝ðＮｉ＝１ｍｉｒ⇀ｉｍꎬ(１)其中ｍ＝ðＮｉ＝１ｍｉꎬ为质点系的总质量.可知ꎬ质心的位矢是以质量为权重的质点系的加权位矢平均值.式(１)两边对时间求导得质心的速度ｖＣ＝ðＮｉ＝１ｍｉｖ⇀ｉｍꎬ(２)或ｍｖ⇀Ｃ＝ðＮｉ＝１ｍｉｖ⇀ｉ可知质点系的总动量等于质心的动量.式(２)两边对时间求导得质心的加速度ａＣ＝ðＮｉ＝１ｍｉａ⇀ｉｍꎬ(３)在惯性系中ꎬ对于质点系ꎬ由牛顿第二定律可得Ｆ外＝ðＮｉ＝１ｍｉａ⇀ｉꎬ(４)其中Ｆ外为质点系所受到的外力的矢量和ꎬ由式(３)和式(４)得Ｆ外＝ｍａ⇀Ｃꎬ(５)由式(５)知ꎬ质心的加速度由质点系受到的外力的矢量和确定ꎬ与质点系的内力无关ꎬ这个结论称为质心运动定理.１.２质心参考系质心参考系是指相对质心不动的参考系ꎬ简称质心系.如果质心相对惯性系做匀速直线运动ꎬ则质心系也是惯性系ꎻ如果质心相对惯性系做加速运动ꎬ３２１则质心系是非惯性系.２例题例１㊀在光滑的水平面上放一半径为ａ㊁质量为Ｍ的圆环ꎬ在某一瞬间有一质量为ｍ的甲虫由静止开始沿此圆环爬行.求甲虫及圆环中心的运动轨迹.解析㊀甲虫和圆环组成的系统受到的外力的矢量和为０ꎬ且甲虫和圆环的初状态都是静止的ꎬ根据质心运动定理知ꎬ甲虫和圆环组成的系统的质心静止不动.甲虫沿圆环爬行ꎬ甲虫到圆环中心的距离不变ꎬ始终为圆环的半径ꎬ故甲虫㊁圆环中心到质心的距离都不变ꎬ分别为ｒ１＝ＭａＭ＋ｍꎬｒ２＝ｍａＭ＋ｍꎬ即甲虫㊁圆环的中心的轨迹都是圆.以系统质心为坐标原点ꎬ甲虫的轨迹方程为ｘ２＋ｙ２＝(ＭａＭ＋ｍ)２ꎬ圆环中心的轨迹方程为ｘ２＋ｙ２＝(ｍａＭ＋ｍ)２.例２㊀一块长为Ｌ的大平板静放在光滑水平面上ꎬ一小孩骑着儿童自行车(小孩和车的大小可忽略不计)以ｖ０的速度从板的一端驶上平板ꎬ在板上他的速度忽快忽慢ꎬ在将近板的另一端时ꎬ他突然刹车ꎬ停在板端.已知人在板上骑车的时间为ｔꎬ板的质量为Ｍꎬ小孩与车的总质量为ｍ.求从车驶上平板到车相对板刚静止时板的位移[１].图１㊀例２示意图例３㊀如图２所示ꎬ用劲度系数为ｋ的轻弹簧连接放在光滑水平面上质量分别为ｍ１㊁ｍ２的木块.让第一个木块紧靠竖直墙ꎬ在第二个木块的侧面上施加水平压力ꎬ将弹簧压缩Ｌ长度ꎬ撤去这一压力后ꎬ求系统质心可获得的最大加速度值和最大速度值.图２㊀例３示意图解析㊀由质心运动定理知ꎬ外力的矢量和最大时ꎬ质心的加速度最大.分析可知刚撤去压力时ꎬ弹簧弹力最大ꎬ竖直墙施加的外力最大ꎬ大小为ｋＬꎬ所以系统质心可获得的最大加速度为ａＣｍ＝ｋＬｍ１＋ｍ２ꎬ此后弹簧弹力减小ꎬ系统质心做加速度减小的加速运动ꎬ直至木块ｍ１离开墙ꎬ系统质心开始做匀速直线运动ꎬ所以木块ｍ１刚离开墙时系统质心的速度最大ꎬ设此速度为ｖＣｍꎬ从撤去压力到木块ｍ１刚离开墙ꎬ系统的机械能守恒:１２ｋＬ２＝１２ｍ２ｖ２２ꎬ其中ｖ２为木块ｍ１刚离开墙时木块ｍ２的速度ꎬ得ｖ２＝Ｌｋｍ２ꎬ由式(２)得系统质心的最大速度ｖＣｍ＝ｍ１ ０＋ｍ２ｖ２ｍ１＋ｍ２＝Ｌｋｍ２ｍ１＋ｍ２.例４㊀三个等质量物块静止地放在光滑平面上ꎬ排成一直线ꎬｍ１＝ｍ２＝ｍ３＝ｍꎬ其中ｍ２和ｍ３用弹性系数为ｋ的弹簧相连ꎬ并保持自然长度ꎬ如图３所示.现在ｍ１以速度ｖ冲向ｍ２ꎬ二者发生完全非弹性碰撞ꎬ求此后的运动中:(１)物块ｍ３的最大动能ꎻ(２)物块ｍ２的最小动能[１].图３㊀例４示意图答案:(１)２９ｍｖ２㊀(２)１７２ｍｖ２４２１例５㊀如图４所示ꎬ长为Ｌ㊁质量线密度为λ的匀质软绳ꎬ开始时绳两端Ａ和Ｂ一起悬挂在天花板上相距较近的两点.Ａ端的天花板能够提供的最大拉力为１.５λＬｇꎬ其中ｇ为当地重力加速度.求:(１)Ｂ端下落多长时间后ꎬＡ端与天花板脱离?(２)Ａ端与天花板脱离后ꎬ经过多长时间绳子完全伸直?图４㊀例５示意图解析㊀(１)以天花板上的Ａ点为原点ꎬ竖直向下为正方向建立ｘ轴ꎬＢ端自由下落ｘ时ꎬ右侧绳子质心的速度为ｕ＝２ｇｘꎬ右侧绳长为Ｌ－ｘ２ꎬ左侧绳子质心的速度始终为０ꎬ整条绳子质心的速度为ｖＣ＝０＋λ(Ｌ－ｘ)２ｕλＬ＝(Ｌ－ｘ)２ｇｘ２Ｌꎬ整条绳子质心的加速度ａＣ＝ｄｖＣｄｔ＝ｇ(Ｌ－３ｘ)２Ｌꎬ计算时应用了ｕ＝ｄｘｄｔꎬ对整条绳子应用质心运动定理得λＬｇ－Ｆ＝λＬａＣꎬ其中Ｆ为天花板对绳子Ａ端的拉力ꎬ即Ｆ＝(Ｌ＋３ｘ)λｇ２ꎬ当Ｆ＝１.５λＬｇ时ꎬｘ＝２３ＬꎬＡ端与天花板脱离ꎬ又ｘ＝１２ｇｔ２１ꎬ得ｔ１＝２３３Ｌｇꎬ为所求的时间.(２)由第(１)问知ꎬＡ端与天花板脱离时ꎬｘ＝２３Ｌꎬ此时Ｂ端的速度ｕＢ＝２ｇｘ＝２３ｇＬ３ꎬ左侧绳子速度为０ꎬ应用式(２)得整条绳子质心的速度ｖＣ＝０＋Ｌλ６ｕＢＬλ＝３ｇＬ９ꎬ此后整条绳子质心和绳子Ｂ端都以加度度ｇ向下做直线运动ꎬ在质心参考系中ꎬ绳子Ｂ端做匀速直线运动ꎬＢ端相对质心的速度ｖｒ＝ｕＢ－ｕＣ＝５３ｇＬ９ꎬ刚脱离时整条绳子质心的坐标为ｘＣ＝１７３６Ｌꎬ绳子Ｂ端坐标为ｘＢ＝２３ＬꎬＢ端到质心的距离为ｘＢ－ｘＣ＝７３６Ｌꎬ绳子完全伸直时Ｂ端到整条绳子质心的距离为Ｌ２ꎬ从Ａ端脱离到绳子完全伸直ꎬＢ端在质心系中的位移Δｘ＝１２Ｌ－７３６Ｌ＝１１３６Ｌꎬ所求时间ｔ２＝Δｘｖｒ＝１１６０３Ｌｇ.综上所述ꎬ应用质心的相关知识解题时ꎬ一般先分析系统所受的外力ꎬ根据质心运动定理ꎬ结合质心的初速度ꎬ判断质心的运动情况ꎬ再分析各质点或系统的各部分相对质心的运动.在质心系中分析问题时ꎬ应注意质心系是惯性系还是非惯性系ꎬ如果质心系是非惯性系ꎬ受力分析时还要考虑到惯性力.解题时还应注意各物理量的值在质心系和其他惯性系(例如地面参考系)中的区别和联系ꎬ计算时不能混淆.参考文献:[１]程稼夫.中学奥林匹克竞赛物理教程力学篇:第２版[Ｍ].合肥:中国科学技术大学出版社ꎬ２０１３(０６):４３６－４３７.[责任编辑:李㊀璟]５２１。

可编辑修改精选全文完整版理论力学题库简答题1-1.简述伽利略相对性原理和牛顿运动定律成立的参考系。

答：（1）内容：不能借助任何力学实验来判断参考系是静止的还是在匀速直线运动；（2）相对与惯性系作匀速直线运动的参考系都是惯性参考系；（3）牛顿运动定理只能在惯性系成立。

1-2. 简述有心力的性质. 并证明质点在有心力作用下只能在一个平面内运动.证明：只要证明角动量是一个常矢量即可.性质：（1）力的作用线始终通过一定点；（角动量是一个常矢量或质点始终在垂直于角动量的平面内运动）(2) 角动量守恒,或掠面速度守恒；(3) 有心力是保守力, 或机械能守恒.1-3.什么情况下质心与几何中心、重心重合？质心系有何特性？(1) 密度均匀物体质心与几何中心重合；(2) 重力加速度为常量时物体质心与重心重合；质心系的特性：(1) 质心系中各质点相对于质心的总动量为零；(2) 质心系的惯性力矩为零；(3) 质心系的惯性力做功为零。

1-4.太阳和地球组成的两体系统中，分别以地球、太阳、质心为参照系，简述地球、太阳的运动情况。

答： （1）质心参照系中地球、太阳的运动：地球，太阳相对于质心作椭圆运动。

（2）地球参照系中太阳运动：太阳相对于地球作椭圆运动。

（3）太阳参照系中地球的运动：地球相对于太阳作椭圆运动。

2-1.分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立的条件。

2-2.说明 质点组 对某定点,如原点O ，的动量矩守恒定律成立的条件（要求写出分量式）。

质点组对原点O 的动量矩守恒定律成立的条件为：0)(1=⨯=∑=e i n i i F r M ，分量守恒。

即： 对x 轴：0)()(1=-∑=e iy i e iz n i i F z F y ；对y 轴：0)()(1=-∑=e iz i e ixn i i F x F z ； 对z 轴：0)()(1=-∑=e ixi e iy n i i F y F x 。

质点系质心位置守恒的条件
质点系质心位置守恒的条件是基于动量守恒定律和质心定义的。

根据动量守恒定律，当质点系内部无外力作用时，系统的总动量守恒。

而质心是质点系统的一种特殊位置，它可以视为质点系的平均位置，具有使得系统动量守恒的特性。

根据质心的定义，质点系质心的位置可以通过质点的质量和位置的加权平均来计算。

具体地说，如果质点系由N个质点组成，其中第i个质点的质量为mi，位于坐标(xi, yi, zi)，则质心的位置可以通过以下公式计算：
X = (m1x1 + m2x2 + ... + mN xN) / (m1 + m2 + ... + mN)
Y = (m1y1 + m2y2 + ... + mN yN) / (m1 + m2 + ... + mN)
Z = (m1z1 + m2z2 + ... + mN zN) / (m1 + m2 + ... + mN)
X、Y和Z分别表示质心在x、y和z坐标轴上的位置。

由于质心的位置是通过加权平均计算得出的，质心的位置不仅依赖于质点们的位置，还与各个质点的质量相关。

当质点系内部无外力作用时，如果不出现质点的质量发生改变的情况，质心的位置应保持不变。

质点系质心位置守恒的条件是质点系内部无外力作用，并且质点的质量不发生改变。

质心系中质点组的运动定律宁国强1. 引言众所周知，牛顿运动定律是在惯性系中低速情况下才成立的规律。

所以，以牛顿运动定律为基础而推导出来的一些运动定律当然也都只能在惯性系中才成立[1~4]。

在研究和解决力学问题时通常选用惯性参考系，但在许多情况下选用非惯性参考系可能会使问题简单化[5~8]。

在非惯性系中引入惯性力以后，牛顿运动定律可以沿用，但其推导出的运动定律是否可以沿用呢？如果可以沿用，其表达式又如何呢？本文将导出质心坐标系（质心坐标系既可以是惯性系，也可以是非惯性系）中质点组的运动定律，并以此为基础讨论质心坐标系中的碰撞与散射现象。

2. 质心参考系以质点组的质心为原点，坐标轴与静止惯性参考系平行，这种参考系称为质心参考系或质心系。

根据质心和质心参考系的定义，可以知道质心参考系的特征。

由质心定义可知，在质心参考系中，质心的位置矢量为.（2-1）0='='∑∑ii i c m r m r将对时间取一阶导数，得c r '.(2-2)0i i c im v v m ''==∑∑由上式知.(2-3)0i i m v '=∑公式（2—3）说明了质点组对质心的总动量为零，这个结论是质心参考系定义的直接结果，与质点组整个系统的运动无关系，它反映出了质心参考系的特征。

因此，我们称质心参考系为零动量参考系。

正是由于有了这一特征，才能使得质心参考系成为讨论质点组运动的重要参考系[9~11]。

质心参考系既可以是惯性系，也可以是非惯性系。

由质心运动定理 可知，我们所研究的系统，如果所∑==dtv d m r m F cci 01受的合外力为零，则质心C 在静止惯性参考系中以恒定速度作惯性运动，此c V时质心参考系也是惯性参考系。

如果所受合外力不为零，则质心相对于静止惯性系作加速运动，这样，质心参考系就不再是惯性参考系，而是非惯性参考系。

3. 质心系中质点组的运动定律3.1 质心系中质点组的动量定理和动量守恒定律若在非惯性系中引入惯性力，则可以导出适用于非惯性系的动量定理，推导如下：设有一质心系(以下简称系)相对另一惯性系（以下简称C x y z '''-k 'O xyz -系）作加速运动，系原点在系中的加速度用表示，现有个质点组成k k 'k c an 的质点系相对系作加速运动，表示各质点相对系原点的位矢，k n r r r ''',,,21k '表示各质点相对于系运动的速度。