质心系中质点组的运动定律

mi ai
i
N
m
质点系的质心运动
质心与质心运动定律
质点系质心运动
质心的特点与求法 质心系
5
质心的求法
(1) 分立质点系的质心
rC
mi ri
i 1
N
m
在直角坐标系下可以表示为：
xC
m x
i
i i
m
, yC
m y
i i
i
m
, zC
m z
i
i i
m
6
D 三质点在某一时刻的位置坐标 B、 例4.1.2-1 A 、
N i
N
ac
Fi
i
质心位置矢量:
rC Biblioteka mi ri m应用： 运动员、炮弹等的轨迹 筛选法（大小土豆） F 0 ，自然界如没摩擦力 的情形设想……
4
质心速度:
drC vC dt
2
mi vi
i
N
m
d rC 质心加速度: a C 2 dt
(4) 多个规则形状物体组成系统的质心
多个规则形状物体组成系统的质心，可先找到每 个物体的质心，再用分立质点系质心的求法，求出公
共质心。
例4.1.2-3 如例4.1.2-3图所示，半径为 R 、质量为 m 、
R 质量分布均匀的圆盘，沿某半径方向挖去半径为 2 的小圆
盘，求大圆盘剩余部分的质心位置。
0, yC y边 ，则系统的质心为：
1 1 R Yc yC dm y边 (2 x边 dy边 ) m m 0
dy边
1 R 4R 2 2 y边 (2 R y边 dy边 ) m 0 3π

物理
例 一段均匀铁丝弯成半圆形，其质量为m，半径为R。
求 此半圆形铁丝的质心。
y
解 选如图所示的坐标系
半圆对y轴对称，则质心应在y轴上
任取一微元长为dl，质量为dm
dm dl m dl
πR 由质心的位置坐标式，有
y R sin dl Rd
yC


ydl
m
C
d
R
dl
y
O
x
大学
3-3 质心运动定理
物理
3.3.1 质心
z
研究由质量为m1, m2 , mn的质点组成
······· F的外质点dd系Pt 质点系动量定理（微分形式）
C× rc
mi
ri
· F外

d dt
(
mivi )
vi

dri dt
F外

d2 dt 2
(
miri )
以m表示质点系的总质量
rC
yc


ydm m
π
yC
Rsin Rd
0
2 R2

m
m
2R π
第三章 守恒定律
4
大学
物理 3.3.3 质心运动定理
F外

m
d2 dt 2
rC

mac
ac称为质心加速度
质心运动定理
3-3 质心运动定理
d 2
F外 m dt 2 (
miri ) m
rC

mi

mi
m
ri
0
y
x
F外

m

第10章 质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力，受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章 质心运动定理
18
例题 图示机构，均质杆OA长l，质量为m1，滑块A的质量为m2， 滑道CD的质量为m3。OA杆在一力偶（图中未画出）作用下作 匀角度ω转动。试求O处的水平约束反力（机构位于铅直平面
内，各处摩擦不计）。 C
A
O
E
D
★理论力学电子教案
第10章 质心运动定理
第10章 质心运动定理
27
ma A
第10章 质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章 质心运动定理
§2 质点系动量、冲量
质点动量： 质点系动量：
p mv
P mivi mvC
问：刚体系动量？
元冲量：
dI F dt
冲量：
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章 质心运动定理
1
第十章 质心运动定理&动量定理
★理论力学电子教案
第10章 质心运动定理

角动量守恒条件
当刚体绕定轴转动时，如果作用于刚体上的外力矩为零，则刚体的 角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题，如陀螺仪的工作原理、 天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时，刚体的角动量将发生变化。此时 需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围：质心运动定律适用于任何由多个质点组成的系统，无论这 些质点之间是否存在相互作用力。
02
适用条件：质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响，或者其影响可以忽 略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小 和方向，等于转动惯量与角速度的 乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时，其质 心位置保持不变，始终位 于转轴上。
质心速度为零
由于质心位于转轴上，因 此质心的速度为零。
质心加速度为零
由于质心速度为零，因此 质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心 的位置矢量称为相对位移。
性质
相对位移是描述质点系内 各点相对于质心位置变化 的物理量，具有矢量性。
计算方法
通过几何方法或解析方法 求出各点相对于质心的位 置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。

第三讲 质心运动定理与刚体转动定律 2018.10.16多个质点构成的系统，假设系统的质量可以集中于一点，这个点即为质量中心，简称质心。

质心是质点系质量分布的平均位置，与重心不同的是，质心不一定要在有重力场的系统中。

值得注意的是，除非重力场是均匀的，否则同一物质系统的质心与重心通常不在同一假想点上。

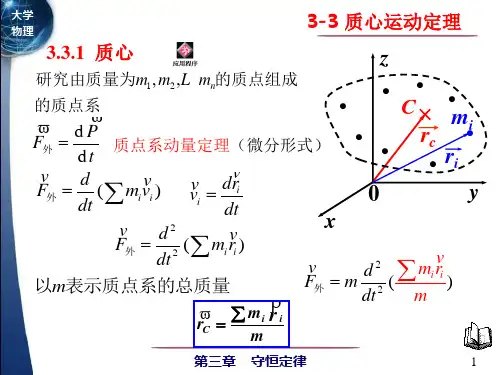
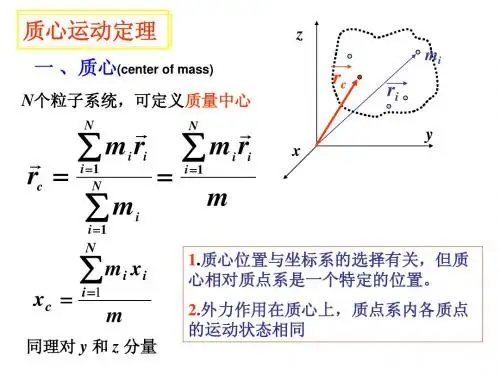
一、质心运动定理设系统由n 个质点组成，各质点的质量分别为n m m m ⋅⋅⋅21、，位矢分别是n r r r ⋅⋅⋅21、，则此质点系质心的位置矢量C r 为nn n C m m m r m r m r m r +⋅⋅⋅+++⋅⋅⋅++=212211 因此，质心的加速度 nn n C m m m a m a m a m a +⋅⋅⋅+++⋅⋅⋅++=212211 设第i 个质点所受的外力为i F ，第j 个质点对第i 个质点所受的作用力为)(i j f ji ≠，则对每个质点应用牛顿第二定律有 11131211a m f f f F n =+⋅⋅⋅+++22232122a m f f f F n =+⋅⋅⋅+++∙∙∙∙∙∙将n 个式子相加，并注意到质点间的相互作用力有ij ji f f -=，得n n n a m a m a m F F F +⋅⋅⋅++=+⋅⋅⋅++221121令F 21=+⋅⋅⋅++n F F F ，称为质点系所受到的合外力，m m m m n =+⋅⋅⋅++21，称为质点系的总质量，则C ma =F这表明，质点系所受的合外力等于质点系的总质量与其质心加速度的乘积，这就是质心运动定理。

二、质心运动守恒定理如果作用于质点系的合外力恒等于零，则质心将处于静止或匀速直线运动状态。

如果作用于质点系的所有外力在某轴上投影的代数和恒等于零，则质心在该轴的方向上将处于静止或匀速直线运动状态。

三、刚体的转动定律刚体是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体，是一种理想模型。

由上式所确定的空间点称质点系的质量中心(质心).
在直角坐标系质心坐标为
xc
mi xi m
yc
mi yi m
zc
mi zi m
对由两个质点组成的质点系，有
xc
m1x1m2x2 m1m2
yc
m1y1m2y2 m1m2
第10页/共19页
x2 xc m1 xc x1 m2
y2 yc m1 yc y1 m2
质心必位于m1与m2的连线上，且质心与各质点距离与质点质量 成反比.
第11页/共19页
[例题3] 一质点系包括三质点，质量为
m2 2单和位
m3
3，单 位置位坐标各为
求质心坐标.
m 1 ( 1 , 2 )m ,2 ( 1 ,1 ) 和 m 3 ( 1 ,2 )
m1 1单位
[解] 质心坐标
xc
m1x1m2x2m3x3 m1m2m3
d p vd tS v
由动量定理
dp vS vF
dt
F表示留在燃烧室内的燃烧物质对排出物质的作用力
Fx Sv2
向下
火箭所受推力，也等于
Sv 2
向上
第5页/共19页
[内例有题质2]量如为图表m0示的传煤送卸带出以，水传平送速带度顶部与将车煤厢卸底入板静v0高止度车差厢为内h。，每开单始位时时车间
第8页/共19页
§3.7.2 质心运动定理
1.质心
质点系动量定理
而
vi
dri dt
i F i d dt(
mivi)
有
i i
F i ddt22(
miri)
F i md dt22(
m iri) m

F
r
2
m1 2
m 2
质心运动定理 动量定理
例2
e 已知：地面水平, 光滑, m1 , m2 , , 初始静止,
常量.
求: 电机外壳的运动.
质心运动定理
动量定理
解:
F (e) x
0
xC1 xC2
质心运动守恒 初始静止
设 xC1 a
xC2
m1(a s) m2 (a esin s)
质心运动定理
n
maC
F (e) i
i 1
是导出定理，描述 质心运动状态变化 规律
动量定理
在直角坐标轴上的投影式为:
质心运动定理
ma
Cx
Fx(e)
maCy
F(e) y
在自然轴上的投影式为:
maCz Fz(e)
m dvC F (e)
dt
t
m vC2
F (e) n
质心运动守恒定律
0
F (e) b
质心运动定理
动量定理
解: 分析整体，受力如图所示。
应用质心运动定理
m1 m2 aCx Fx F
xC
m1
r 2
cos
m2 r cos
b
m1
1 m2
aCx
d 2Cx dt 2
r 2
m1 m2
m1 2
m2
c o s
t
Fx
F
r
2
m1 2
m2
c o s
t
最大水平约束力为
Fmax
动量定理
内力不能改变质心的运动
汽车发动机的气体
地面摩擦力
动量定理
n
maC

xc
mi xi
i 1
N
m
同理对 y 和 z 分量
m1
l1
r1
rc
l2
m2
r2
m1 (rc r1 ) m2 (r2 rc )
m1l1= m2l2
m1 r1 m2 r2 rc m1 m 2
O
对连续分布的物质，可以将其分为N个小质元
质心运动定理
一 、质心(center of mass)
N个粒子系统，可定义质量中心
z
mi
rc
ri
y
rc
m i ri
N i 1 N
mi
i 1

m i ri
N i 1
x
m
1.质心位置与坐标系的选择有关，但质 心相对质点系是一个特定的位置。 2.外力作用在质心上，质点系内各质点 的运动状态相同
dt
dt
1.内力不改变质心的运动状态，但可以改变各质点的运动状态 如炮弹爆炸时，质心轨迹为抛物线
2.质点系所受合外力为零，则动量守恒，此时质心的速度不变
i
质心的运动只与系统所受的合外力相关
drc d ri 质点系的总动量 m m i v i dt dt dv c dP总 mv c mi v i m P总
m ac F
F外 mac
rc
xc
r dm m xdm
m
Z
Y
r
O
X
dm
例： 一均匀直杆，质量为M，长为L, 求其质量中心
解：1、建立坐标系 2、取微元dx dm=dx, 坐标为x
0

25
第26页/共31页
例 5 三棱体C，滑块A和B各面均光滑，初始 时
三者3相00对水平=6桌00面静止。已知mc = 4ma
=16mb , .求A下降h=10cm时，
三棱体C沿水平方向的位移。
26
第27页/共31页
例 三棱体C，滑块A 和B各面均光滑，初始 时三者相对水平桌面静 止。三棱体C沿水平方 解向的水位平方移向。动量守恒。右为 x 正方向
第31页/共31页
柔软链条，其单位长度的质
量为 ．将其卷成一堆放在
地面． 若手提链条的一端，
y c
yC o
以匀速v 将其上提．当一端
被提离地面高度为 y 时，求手的提力．
第15页/共31页
解 建立图示坐标系 链条质心的坐标yc是变化的
y F
mi yi λy y λ(l y) 0
yc i
mi
2
λl
i
y2
运动前后，位置的改变
28
第29页/共31页
运动前后，位置的改变
mAxA mBxB mCxC C 0
xA x'A xC ; xB x'B xC
xC
mAx 'A mBx 'B mA mB mC
x 'A h / tg
x 'B
h
sin
cos
29
第30页/共31页
感谢您的观看！
30
mA
dxA dt
mB
dxB dt
mC
dxC dt
0
d dt
(mA xA
mB xB
mC
xC
)
0
mA xA mB xB mC xC C

第２２卷第２期　２００７年６月　邢台学院学报　ＪＯＵＲＮＡＬ　ＯＦ　ＸＩＮＧＴＡＩ　ＵＮＩＶＥＲＳＩＴＹ　Ｖ０ｌ＿２２．Ｎｏ．２　

Ｊｕｎｅ．２００７　

内力对质点组质心运动的影Ｄｉ５　封素芹，王建勇　（邢台学院物理系，河北邢台０５４００１）　

摘要：在一般力学教材中，均强调内力不改变质点组质心的速度．实际上，内力在一定条件下，也会对质心的速度产　生一定影响．　关键词：质・Ｃ．２；内力；外力　中图分类号：０３１　文献标识码：Ａ　文章编号：１６７２—４６５８（２００７）０２—０１０６—０２　

１　质点组质心运动定理　假设一质点组由ｎ个质点组成，它们的质量分别为　ｍ。，ｍ　，…，ｍ　，质点对指定参考点０的位矢分别为　，　，…，　ｒｎ，则此质点组的质心Ｃ对同一参考点的位矢　满足如下关系　ｍ　ｍ　ｃ　＿　∑ｍ　“‘　式中ｍ：∑ｍ　为质点组的总质量．　选参考点０为惯性系的坐标原点，作用在质点ｍ　上的　诸力的合力　表示为内力　‘　和外力　‘　之和，由牛顿　第二定律可得质点　的运动微分方程为：　ｍ等２－－＋：　＋　ｌ＇２，…，　（２）　对质点组中每个质点均可写出这样一个微分方程，共　ｎ个，将这ｎ个方程加起来则得：　∑ｍ　＝∑　㈨＋∑　㈨（　ｌ＇２，…，ｎ）　（３）　而由牛顿第三定律可知，内力之矢量和为零，于是（３）　式变为：　ｎ　一　ｎ　ｍ　ｄｚ　ｒｉ＝　（　＝ｌ，２，…，ｎ）　（４）　结合（１）式可得：　２　ｄｚ　ｍ　ｒｃ＝　㈨　ｌ，２，…，ｎ）　（５）　，２　式中　是质心的加速度，（５）即为质心运动定理．　２　内力对质心运动的影响　质心运动定理表明，质心的运动像一个质点的运动一　样，此质点的质量等于整个质点组的质量，作用在该质点上　的力，等于作用在质点组上所有外力的矢量和．这就是质心　运动定理．如果质点组不受外力（或所受外力的矢量和等　于零），则质点组质心的速度保持不变．即内力不会影响质　心的运动状态．从方程（５）显然能得到上述结果．教材中所　列举的例子加上生活中的一些实例好像也能说明这一点．　例如：沿水平方向发射的大炮，如果不计水平方向上可能的　外力（如地面摩擦力、空气阻力等），将炮弹与炮身看成一　质点组，炮弹发射后，炮身向后反冲，在水平方向上质点组　动量仍保持为零．跳水运动员无论在空中作多复杂的动作，　其质心均将沿抛物线运动．但是，我们所见到的并不能穷尽　所有，不能由这几个特例去得到一个普适的规律．因为几个　特例并不能代表普遍情况．　从物理角度来分析，若外力与质点的位置或速度有关，　由于内力的影响各质点作不同的运动，各质点所处的位置　不同或速度不同时，质点所受外力也将变化，这样内力就会　通过影响外力，进而影响到质心的运动．这从数学角度分析　也是合理的．一般情况下质点所受的力是时间ｔ、位矢ｒ及　

动量定理 角动量定理（第四章讲） 动能定理
动量守恒定律 角动量守恒定律（第四章讲） 机械能守恒定律
时间累积效应
空间累积效应
牛二律，瞬时效应
动量定理
角动量定理
动能定理
木块：
蚂蚁：
系统的质心为
蚂蚁在斜面底端左边时，设木块向右运动xM，则蚂蚁的坐标为 ，此时系统的质心位置为
系统的质心位置为
除了上面的解法外，你还可以用什么方法解此题？
【例题3－10】长度为L、质量为M的船停止在静水中（但未抛锚），船尾上有一个质量为m的人，也是静止的。现在令人在船上开始向船头走动，忽略水的阻力。试问：当人走到船头时，船将会移动多远？
连续质量分布，积分形式
在直角坐标系中可写成分量式：
3－13 物体的质心处是否必定在物体上？质心与重心是否一定重合？
【例题3－14】求腰长为a的等腰直角三角形均匀薄板的质心位置。
a
O
dy
y
y
x
解：取如图所示的质量元，有
【补充题】
xБайду номын сангаас
y
R
R/2
解：
（1）由对称性知： yc=0
（2）用填补法：设面密度为
R/2
求如图所示均匀薄板的质心位置。
二、质心运动定律
质心速度：
质心加速度：
质心运动定理
…………………………………………
利用内力互为反作用力：
将上式相加
得：
质心运动定理：不管物体的质量如何分布，也不管外力作用在物体的什么位置上，质心的运动就象是物体的全部质量都集中于此，而且所有外力也都集中作用其上的一个质点的运动一样，这应是质心运动定律。它表明，质心的运动服从牛顿第二定律，系统内力不会影响质心的运动。

系统动量守恒 , 即
pN
2 12 ν
1
pe + p ν + p N = 0
又因为
pν
pe ⊥ pν
∴ pN = ( p + p )
2 e
22
代入数据计算得
p N = 1 .36 × 10
kg m s
pe α = arctan = 61.9° pν
第四章动量定理与动量守恒定律 4 – 3 质心 质心运动定理
第四章动量定理与动量守恒定律 4 – 3 质心 质心运动定理
令:
为质点的总
质量, 并令 则有
m = ∑mi
d2rc m 2 = F(e) dt
rc
∑m r =
m
i i
质心运动方程
rc 质心 我们把前式定义的位置矢量 的矢端处的几何点C, 称为质点系的质量中心, 简称质心. 1) 离散分布的质点系的质心位置(直角坐标
第四章动量定理与动量守恒定律 4 – 3 质心 质心运动定理 两体问题 质量分别为m1和m2的两个相互作用的质点组成的 质量分别为 质点系, 就是所谓两体问题 两体问题. 质点系 就是所谓两体问题 两质点在惯性系K 两质点在惯性系 中速度分别是 v 和 v , 在质心 1 2 系C中速度是 v1′ 和 v2′ , 于是两质点的相对速度 u为: 中速度是 由于是质心系. u = v1 v2 = v1 v2 由于是质心系 ′ ′ 两式联立, m v1 + m2v2 = 0 两式联立 解得 1 m2u mu ′ ′ 1 v1 = , v2 = m + m2 m + m2 1 1
系)
rc → xc
∑m x , y = ∑m y , z = ∑m z =

例3 有质量为2m的弹丸，从地面斜抛出去，它的落 地点为xC 。如果它在飞行到最高点处爆炸成质量相 等的两碎片。其中一碎片铅直自由下落，另一碎片水 平抛出，它们同时落地。问第二块碎片落在何处。
解： 在爆炸的前后，质心始终
只受重力的作用，因此， 质心的轨迹为一抛物线， 它的落地点为xc 。
m1 x1 m2 x2 xC m1 m2 mx2 xC 2m
dV r 2 dz
而
r a sin z a cos , 2 dV a sin d a cos
a 1 cos d cos
3 2
r a sin
z
z a cos x


a

0 设 u cos ，则 v z dV zdV a 4 1 1 u2 udu 2 a 3 zc 0 3 V dV
x1c R
y
O
x
1 2 小圆板质量为 m1 R， 4 质心坐标为
2
3 余下的质量为 m2 R 2，质心坐标用 x 2 c表示，则 4
1 3 2 R R R 2 x2 c 2 4 0 4 2 R
R x2c 6
例2
求半径为a的均质半圆球的质心
解：如图，以球心O为原点建立坐标系.将半球体划 分为若干半径为r厚为dz的平板状薄圆，体积元为dV
令
m1r1 m2 r2 rc m1 m2
（2）n个质点系统
分量形式
xc
i
rc
mi ri
m
i
i i
i
i
m x m
i i i
i

质心运动定理的表示方法
直角坐标表示法：
自然表示法：
maCx
m
d 2 xC dt 2
FixE
maCy
m
d 2 yC dt 2
FiyE
maCz
m
d 2zC dt 2
FizE
maC
m dvC dt
FiE
maCn
m vC2
FinE
maCb 0 FibE
︵。︵
10
HOHAI UNIVERSITY ENGINEERING MECHANICS
练习1： 质量50kg，长度2 2m的均质杆A端搁在光滑水平面
上，另一端B与水平杆BD铰接并用铅直绳BE悬挂。已知系统
静止于图示位置，在绳突然剪断瞬间，B点的加速度为
7.35m/s2，方向铅垂向下。试求此瞬时水平面对AB杆的反力。
BD杆质量不计。
解：1.
2.
受力分析； 运动分析；
y
以B为基点，分析A点加速度：
得：
FN
FN
mg
maCy
mg m aB 2 ︵。︵
例3: 质量m，半径r的均质圆轮在一个力偶作用下，沿
水平面纯滚动。已知某时刻轮上最前点A的加速度为
aA，方向如图。试求：（1）质心的加速度；（2）圆 轮所受摩擦力的大小。
解：
aO
3aA 2
2.受力分析
M
C aO mg
3.质心运动定理
maO F
FN F
F
3 2
ma
A
︵。︵
23
HOHAI UNIVERSITY ENGINEERING MECHANICS
设电动机轴以匀角速ω转动，求螺栓和基础作用于电

3-2 质心和质心运动定理 ——基于整体运动的视角 基于整体运动的视角—— 基于整体运动的视角
牛顿定律只适用于质点
v v F = ma
由于质点系中各质点的运动情况各不相同， 由于质点系中各质点的运动情况各不相同，加速度也 不尽相同， 不尽相同，所以质点系的运动情况不能简单地等效成
v v F外 = mac
但对质点系而言， 但对质点系而言，确 实存在一个特殊的点， 实存在一个特殊的点， 能够使上式成立
当球棒从手中抛出后， 当球棒从手中抛出后，球棒在做上抛运动的同时还在 旋转，这时球棒上各点的运动比较复杂， 旋转，这时球棒上各点的运动比较复杂，但球棒上有 一点的运动却简单得象一个质点一样， 一点的运动却简单得象一个质点一样，沿抛物线的轨 迹运动
v d v v v (m1r1 + m2r2 + L + mn rn ) = ∑ Fi外 dt 2
质点化” 如何使质点系的运动规律 “质点化”呢？
2
v v v v d m1r1 + m2r2 + L + mn rn (m1 + m2 + L + mn ) 2 ( ) = ∑ Fi外 m1 + m2 + L + mn dt
跳水者不管在空 中作多复杂的动 作，其质心仍然 是沿抛物线运动
例1 一炮弹在轨道最高点炸成质量比m1:m2=3:1的两个 一炮弹在轨道最高点炸成质量比 的两个 碎片。其中m 自由下落， 碎片。其中 1自由下落，落地点与发射点的水平距离 继续向前飞行， 同时落地。 为R0，m2继续向前飞行，与m1同时落地。不计空气阻 的落地点。 力，求m2的落地点。
这个在质点系上的特殊点是什么，它又在哪里？ 这个在质点系上的特殊点是什么，它又在哪里？