高阶系统的零、极点分析 自控课设
- 格式:docx
- 大小:562.55 KB
- 文档页数:23

目录1系统稳定性分析 (1)2高阶系统的时域响应 (2)2.1系统单位阶跃响应曲线 (2)2.2系统单位斜坡响应曲线 (4)2.3系统单位加速度响应曲线 (5)2.4动态性能指标计算 (6)2.4.1动态性能指标计算 (6)2.4.2动态性能指标计算 (6)2.5 稳态性能指标计算 (9)3根轨迹图绘制 (10)3.1根轨迹数据计算 (10)3.2用MATLAB绘制根轨迹图 (11)4心得体会 (12)参考文献 (13)本科生课程设计成绩评定表高阶系统的时域分析1 系统稳定性分析给定参数系统稳定性分析: 对于开环传递函数))(95()()(2a s s s s b s K s G p ++++=在给定条件K=15,a=2,b=4时用劳斯判据判断系统的稳定性,经过化简可得系统的特征方程为:D(s)=S 4+7S 3+19S 2+33S+60=0其劳斯表为S 41 19 60 S 3 7 33 0 S2 14.3 60 S 1 3.6 0 S 0 60从表中可以看出,第一列系数符号全部为正,故系统是稳定的。
2高阶系统的时域响应K=15,a=2,b=4时,系统的开环传递函数为:G p=15(s+4)s(s2+5s+9)(s+2)=15s+60s4+7s3+19s2+18s系统为Ⅰ型系统,可以跟踪单位阶跃信号、单位斜坡信号,不能跟踪单位加速度信号。
系统响应为C(s)=15s+60s4+7s3+19s2+33s+60R(s)2.1系统单位阶跃响应曲线当输入为单位阶跃函数信号时,R(s)=1S,系统响应为C(s)=15s+60s4+7s3+19s2+33s+60·1S运用MATLAB程序作图如图2-1,程序为:num=[15 60];den=[1 7 19 33 60];G=tf(num,den);step(G);grid on;xlabel('t');ylabel('c(t)');title('单位阶跃响应')图2-1 系统阶跃响应由图中数据可得:上升时间为t=1.02sr峰值时间=1.73stp调节时间=33.1sts超调量σ%=78%稳态误差为=0ess当输入为单位斜坡函数信号时,R(s)=1s2,系统响应为C(s)=15s+60s4+7s3+19s2+33s+60·1s2运用MATLAB程序作图如图2-2,程序为:num=[15 60];den=[1 7 19 33 60];G=tf(num,den);t=0:0.01:10;u=t;lsim(G,u,t);grid on; xlabel('t');ylabel('c(t)');title('单位斜坡响应')图2-2 单位斜坡响应当输入为单位加速度函数信号时,R(s)=1s3,系统响应为C(s)=15s+60s4+7s3+19s2+33s+60·1s3运用MATLAB程序作图如图2-3,程序为:num=[15 60];den=[1 7 19 33 60];G=tf(num,den);t=0:0.01:10;u=(0.5*t.^2);lsim(G,u,t)grid on;xlabel('t');ylabel('c(t)');title('单位加速度响应')图2-3 单位加速度响应2.4动态性能指标计算2.4.1主导极点法控制系统的暂态性能指标通常是零初始条件下,通过系统的阶跃响应的特征定义的,系统的暂态性能指标实际上就是刻画阶跃响应曲线特征的一些量。

自动控制原理的零点和极点一、引言自动控制原理是研究如何通过系统的输入和输出之间的关系,设计出能够稳定控制系统的方法和技术。
在自动控制系统中,零点和极点是两个重要的概念。
本文将从零点和极点的概念、特性以及在自动控制系统中的应用等方面进行详细阐述。
二、零点的概念和特性零点是指系统传递函数的分子为零的根,也就是使得系统输出为零的输入值。
在自动控制系统中,零点可以用来描述系统对于某些输入的抑制作用。
一个系统的零点越多,其对应的输入越容易被抑制,从而对系统的稳定性和鲁棒性有着重要影响。
零点的特性有以下几点:1. 零点可以是实数根,也可以是复数根;2. 零点的数量等于系统传递函数的分子次数;3. 零点可以是系统稳定性的重要指标,对于系统的抑制作用起到关键性的作用。
三、极点的概念和特性极点是指系统传递函数的分母为零的根,也就是使得系统的输出趋于无穷大的输入值。
在自动控制系统中,极点可以用来描述系统的稳定性和响应速度。
一个系统的极点越多,其对应的系统响应越不稳定,从而对系统的控制性能有着重要影响。
极点的特性有以下几点:1. 极点可以是实数根,也可以是复数根;2. 极点的数量等于系统传递函数的分母次数;3. 极点的位置对系统的稳定性和响应速度有着决定性的影响。
四、零点和极点的关系在自动控制系统中,零点和极点之间存在着重要的关系。
通过对零点和极点的分析,可以得到系统的稳定性和控制性能等重要信息。
一般来说,当系统的极点位于左半平面时,系统是稳定的;当系统的极点位于右半平面时,系统是不稳定的。
而零点的位置则决定了系统对于某些输入的抑制作用。
在设计自动控制系统时,可以通过调整零点和极点的位置来达到所需的控制效果。
例如,可以通过增加零点的数量来提高系统对特定输入的抑制能力;可以通过移动极点的位置来改善系统的稳定性和响应速度。
五、零点和极点在自动控制系统中的应用零点和极点在自动控制系统中有着广泛的应用。
以下是一些常见的应用场景:1. 稳定性分析:通过对系统的极点位置进行分析,可以判断系统是否稳定。

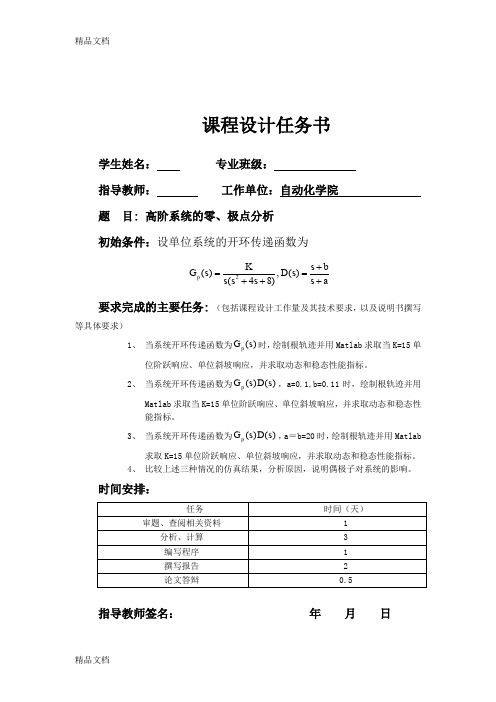
课程设计任务书学生姓名: 专业班级:指导教师: 工作单位:自动化学院题 目: 高阶系统的零、极点分析 初始条件:设单位系统的开环传递函数为2(),()(48)p K s bG s D s s s s s a+==+++要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 当系统开环传递函数为()p G s 时,绘制根轨迹并用Matlab 求取当K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
2、 当系统开环传递函数为()()p G s D s ,a=0.1,b=0.11时,绘制根轨迹并用Matlab 求取当K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
3、 当系统开环传递函数为()()p G s D s ,a =b=20时,绘制根轨迹并用Matlab 求取K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
4、 比较上述三种情况的仿真结果,分析原因,说明偶极子对系统的影响。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名:年月日目录摘要 (I)1 线性高阶系统的零极点分析简介 (2)2 线性高阶系统的数学模型 (3)3 高阶系统零极点分布对系统性能影响分析 (4)3.1系统开环传递函数为()pG s的根轨迹 (4)3.1.1系统开环传递函数为()pG s,单位阶跃输入时的根轨迹 (5)3.1.2系统开环传递函数为()pG s,单位斜坡输入时的根轨迹 (6)3.1.3动态性能、稳态性能分析 (7)3.1.4参考程序法 (8)3.2系统开环传递函数为()()pG s D s(a=0.1,b=0.11)的根轨迹 (9)3.2.1系统开环传递函数为()()pG s D s,单位阶跃输入时的根轨迹 (9)3.2.2系统开环传递函数为()()pG s D s,单位斜坡输入时的根轨迹 (10)3.2.3动态性能、稳态性能分析 (11)3.3系统开环传递函数为()()pG s D s(a=b=20)的根轨迹 (12)3.3.1系统开环传递函数为()()pG s D s,单位阶跃输入时的根轨迹 (13)3.3.2系统开环传递函数为()()pG s D s,单位斜坡输入时的根轨迹 (13)3.3.3动态性能、稳态性能分析 (14)4 分析比较 (16)4.1三种仿真结果的比较: (16)4.2高阶系统偶极子对系统性能的影响 (16)4.3 综合分析 (18)5 心得体会 (19)参考文献 (20)摘要三阶及三阶以上的系统通常称为高阶系统,即用高阶微分方程描述的系统。


matlab零极点 课程设计一、课程目标知识目标:1. 理解并掌握Matlab中零极点的基本概念及其在控制系统中的应用;2. 学会使用Matlab进行零极点图的绘制和分析;3. 掌握零极点对系统稳定性的影响,能运用相关知识分析简单控制系统的性能。
技能目标:1. 能够运用Matlab软件进行零极点图的绘制;2. 能够通过零极点分析判断控制系统的稳定性;3. 能够运用所学知识解决实际问题,提高解决复杂工程问题的能力。
情感态度价值观目标:1. 培养学生对控制理论及其应用的兴趣,激发学习积极性;2. 培养学生的团队协作意识和沟通能力,使学生能够在小组讨论中积极参与,共同解决问题;3. 培养学生的创新意识和实践能力,使学生能够主动探索新知识,勇于尝试新方法。
本课程针对高年级本科或研究生阶段的学生,结合课程性质、学生特点和教学要求,将课程目标分解为具体的学习成果。
通过本课程的学习,学生将能够掌握Matlab零极点相关理论知识,具备运用Matlab分析控制系统稳定性的能力,并培养积极的情感态度和价值观。
为实现这些目标,后续教学设计和评估将围绕这些具体学习成果展开。
二、教学内容1. 理论知识:- 控制系统的基本概念与原理;- 零点、极点的定义及其在控制系统中的作用;- 零极点与系统稳定性的关系;- Matlab中零极点分析的相关函数。
2. 实践操作:- 使用Matlab软件绘制零极点图;- 分析零极点对控制系统性能的影响;- 案例分析:选取实际控制系统,运用零极点分析判断稳定性。
3. 教学大纲:- 第一周:控制系统基本概念与原理回顾;- 第二周:零点、极点及其在控制系统中的应用;- 第三周:零极点与系统稳定性的关系;- 第四周:Matlab中零极点分析相关函数的使用;- 第五周:实践操作,绘制零极点图及分析;- 第六周:案例分析,综合运用所学知识。
教学内容参考教材相关章节,结合课程目标进行选择和组织,确保内容的科学性和系统性。
课程设计题目高阶系统性能分析学院专业班级姓名指导教师2012年1月4日课程设计任务书学生姓名: 专业班级: 指导教师: 工作单位: 题 目: 高阶系统性能分析 初始条件:设单位系统的开环传递函数为122(1)()(24)(1)p K s G s s s s s ττ+=+++ 要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 当120ττ==时,绘制根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标2、 当12120.2,05,0ττττ====和时,分别绘制闭环系统根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标 3、 当12120,0.20,5ττττ====和时,分别绘制闭环系统根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标 4、 比较上述三种情况的仿真结果,分析原因,说明增加零极点对系统性能的影响。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日目录引言 (1)1 三阶系统的性能分析 (2)1.1绘制根轨迹图 (2)1.2求取单位阶跃响应 (3)1.3求取单位斜坡响应 (4)1.4求取性能指标 (5)2 增加一个开环零点 (7)2.1绘制根轨迹图 (7)2.2求取单位阶跃响应 (9)2.3求取单位斜坡响应 (11)2.4求取性能指标 (12)3 增加一个开环极点 (14)3.1绘制根轨迹图 (14)3.2求取单位阶跃响应 (16)2.3求取单位斜坡响应 (18)3.4求取性能指标 (19)4 结果分析 (21)4.1开环增益对系统的影响 (21)4.2增加开环零极点对系统性能的影响 (22)结束语 (24)参考文献 (25)附录手工绘制根轨迹的步骤 (26)引言在现代科学技术的众多领域中,自动控制技术起着越来越重要的作用。
所谓自动控制,是指在没有人直接参与的情况下,利用外加的设备或装置(称控制装置或控制器),使机器设备或生产过程(统称被控对象)的某个工作状态或参数(即控制量)自动地按照预定的规律运行。
现代工程控制理论实验报告实验名称:高阶系统闭环零极点对系统特性的影响目录一、实验目的 (3)二、实验原理 (3)1、高阶系统动态性能分析 (3)2、系统的零极点的分布对系统的影响如下: (4)三、实验过程 (4)1、绘制增加极点前后系统y1,y2的阶跃响应曲线。
(4)2、绘制增加零点前后系统y1,y3的阶跃响应曲线。
(6)3、绘制增加远离虚轴的偶极子前后系统y1和y4的阶跃响应曲线 (7)4、绘制增加靠近虚轴的偶极子前后系统y1和y5的阶跃响应曲线 (8)四、实验结果及分析 (10)1、绘制增加极点前后系统y1,y2的阶跃响应曲线。
(10)2、绘制增加零点前后系统y1,y3的阶跃响应曲线。
(10)3、绘制增加远离和靠近虚轴的偶极子前后系统的阶跃响应曲线 (10)4、通过以上理论分析和仿真验证可得到以下结论: (10)五、实验中存在问题 (11)一、 实验目的1、 增加或减少闭环零极点及闭环零极点的位置来研究高阶系统的动态性能指标。
2、学习用工程软件MATLAB 通过编程来绘制系统的阶跃响应曲线。
3、研究系统的零极点及偶极子对系统控制特性的影响。
二、 实验原理1、高阶系统动态性能分析高阶系统的闭环传递函数的一般形式可表示为:11110111)()()(a s a s a s a b s b s b s b s R s C s G n n n n m m m m ++⋅⋅⋅++++⋅⋅⋅++==---- (n ≥m )表示成零极点形式后,为:∏∏==++=niimj j p s z s K s G 11)()(式中:-z i (i=1,2,...,m)---闭环传递函数的零点 -p j (j=1,2,…,n)---闭环传递函数的极点。
假设系统闭环零极点都互不相同,且均为单重的。
则单位阶跃响应的拉氏变换为:2、系统的零极点的分布对系统的影响如下:①、若某极点远离虚轴与其它零、极点,则该极点对应的响应分量较小。
题 目: 高阶系统的零、极点分析 初始条件:设单位系统的开环传递函数为2(),()(48)p K s bG s D s s s s s a+==+++要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 当系统开环传递函数为()p G s 时,绘制根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标2、 当系统开环传递函数为()()p G s D s ,a=0.1,b=0.11时,绘制根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标3、 当系统开环传递函数为()()p G s D s ,a =b=20时,绘制根轨迹并用Matlab 求取单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标4、 比较上述三种情况的仿真结果,分析原因,说明偶极子对系统的影响。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日摘要本次课程设计的主要任务是对高阶系统零、极点的分析。
一个控制系统的好坏,主要是从系统的稳定性、准确性和快速性三个方面来进行描述的。
此次课程设计主要是利用MATLAB绘制高阶系统的根轨迹,了解高阶系统零、极点的分布情况,求取高阶系统的单位阶跃响应和单位斜坡响应,并分析系统的动态和稳态性能指标。
通过增加系统零、极点,求解不同闭环传递函数下系统的各项性能指标,来分析总结零、极点和偶极子对于高阶系统的影响。
关键字:劳斯稳定判据根轨迹零极点稳定要求性能指标高阶系统的零、极点分析1系统稳定性分析劳斯稳定判据:系统稳定的充分必要条件是劳斯表中的第一列数的符号完全相同。
如果劳斯表中的第一列的符号不完全相同,则系统不稳定。
而且,系统正实部特征根的个数等于劳斯表第一列数的符号变化次数。
根据已知条件可知,所研究系统的开环传递函数:22()()()()(48)(48)()k p K s b K s b G s G s D s s s s s a s s s s a ++=∙=∙=++++++ 由开环传递函数可得其闭环特征方程为:432(4)(84)(8)0s a s a s a K s bK +++++++=劳斯表如下:4s 1 84a + bK 3s 4a + 8a K + 02s 2416324a a K a++-+ bK1s 224163241632[(8)(4)]44a a K a a Ka K a bK a a++-++-⨯+-+⨯++ 00s bK根据劳斯判据可知,系统稳定,则劳斯表中第一列数的符号完全相同。
课程设计任务书学生姓名: 专业班级:指导教师: 工作单位:自动化学院题 目: 高阶系统的零、极点分析 初始条件:设单位系统的开环传递函数为2(),()(48)p K s bG s D s s s s s a+==+++ 要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 当系统开环传递函数为()p G s 时,绘制根轨迹并用Matlab 求取当K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
2、 当系统开环传递函数为()()p G s D s ,a=0.1,b=0.11时,绘制根轨迹并用Matlab 求取当K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
3、 当系统开环传递函数为()()p G s D s ,a =b=20时,绘制根轨迹并用Matlab 求取K=15单位阶跃响应、单位斜坡响应,并求取动态和稳态性能指标。
4、 比较上述三种情况的仿真结果,分析原因,说明偶极子对系统的影响。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名:年月日目录摘要 (I)1 线性高阶系统的零极点分析简介 (2)2 线性高阶系统的数学模型 (3)3 高阶系统零极点分布对系统性能影响分析 (4)3.1系统开环传递函数为()pG s的根轨迹 (4)3.1.1系统开环传递函数为()pG s,单位阶跃输入时的根轨迹 (5)3.1.2系统开环传递函数为()pG s,单位斜坡输入时的根轨迹 (6)3.1.3动态性能、稳态性能分析 (7)3.1.4参考程序法 (8)3.2系统开环传递函数为()()pG s D s(a=0.1,b=0.11)的根轨迹 (9)3.2.1系统开环传递函数为()()pG s D s,单位阶跃输入时的根轨迹 (9)3.2.2系统开环传递函数为()()pG s D s,单位斜坡输入时的根轨迹 (10)3.2.3动态性能、稳态性能分析 (11)3.3系统开环传递函数为()()pG s D s(a=b=20)的根轨迹 (12)3.3.1系统开环传递函数为()()pG s D s,单位阶跃输入时的根轨迹 (13)3.3.2系统开环传递函数为()()pG s D s,单位斜坡输入时的根轨迹 (13)3.3.3动态性能、稳态性能分析 (14)4 分析比较 (16)4.1三种仿真结果的比较: (16)4.2高阶系统偶极子对系统性能的影响 (16)4.3 综合分析 (18)5 心得体会 (19)参考文献 (20)摘要三阶及三阶以上的系统通常称为高阶系统,即用高阶微分方程描述的系统。
在控制工程中,高阶系统非常普遍,而分析起来却十分复杂。
在自动控制系统中,对系统的各项性能如稳定性、动态性能和稳态性能等有一定的要求。
稳定性是控制系统的本质,指的是控制系统偏离平衡状态后自动回复到平衡状态的能力。
系统动态性能是在零初始条件下通过阶跃响应来定义的,对于稳定的系统,动态性能一般指的系统的超调量、超调时间、上升时间、调整时间,描述的是系统的最大偏差以及反映的快速性;稳态性能指的是系统的稳态误差,描述的是系统的控制精度。
在本文中,主要分析高阶系统的各项性能指标,对于高阶系统,分析其各项性能指标有很多方法,本文采用高阶零级点的分布来研究系统的各项性能指标,主要借助工程软件Matlab通过编程来绘制系统的根轨迹与阶跃响应、斜坡响应曲线,研究系统的零极点分布,进而分析系统的各项性能指标。
关键词:自动控制动态性能稳态性能高阶系统阶跃响应斜坡响应高阶系统的零、极点分析1 线性高阶系统的零极点分析简介线性系统的动态性能与系统的闭环零极点在S 平面的分布有着密切的联系,系统的开环零极点一般是比较容易求得的,但对于高阶系统,利用古典的分解因式的方法求闭环特征方程的极点是十分困难的,当系统的某一参数发生改变时,需要反复的求解特征方程的根,从而研究系统的动态性能。
这里,选用根轨迹的方法研究闭环系统零极点分布对系统性能的影响。
当闭环传递函数在S 平面的右半平面存在极点时,系统是不稳定的;只有闭环传递函数的极点均位于S 平面的左半平面,系统才稳定;当闭环极点位于坐标虚轴上时,系统临界稳定。
如果闭环系统无零点且闭环极点均为实数极点,则系统的响应是单调的;如果闭环极点均为复数极点,那么响应一般是振荡的。
闭环系统的超调量%p σ主要由闭环传递函数复数主导极点的衰减率1//d σωζ=决定,而且还与其它闭环零、极点接近坐标原点的程度密切相关。
闭环系统的调节时间s t 主要取决于最靠近虚轴的闭环复数极点实部绝对值1σ=n ζω;如果实数极点距离虚轴最近而且其附近没有实数零点,则系统的调节时间主要由该极点的模值决定。
给闭环控制系统增加零点减小了系统的阻尼比,使系统的超调时间p t 减小,超调量%p σ增大,而闭环系统的极点增大了系统的阻尼比,使系统的超调时间变长,而超调量减小。
闭环零极点的对高阶系统性能的影响随其接近坐标原点的程度而增强。
2 线性高阶系统的数学模型系统的闭环传递函数为()()()()1()()C s G s s R s G s H s Φ==+ (2-1) 式(1)中,R(s)为系统输入的Laplace 变换,C (s )为系统输出的Laplace 变换,G(s)为前向通道传递函数,H(s)为反馈传递函数。
在一般情况下,G (s )和H(s)都是s 的多项式之比,故式(1)可以写1()011(),1()011m m b s b s b s b M s m m s m n n n D s a s a s a an n-++++-Φ==≤-++++- (2-2) 为了便于求取高阶系统的单位阶跃输入响应和单位斜坡输入响应,一般将式(2)的分子多项式和分母多项式利用根轨迹法进行因式分解,写成如下因式的乘积形式11()()()()()()()mi i njj K s z C s M s s R s D s s s ==-Φ===-∏∏ (2-3)式(3)中,i z 为闭环系统的零点,j s 为闭环系统的极点,K 为开环根轨迹增益。
由于M(s)和D(s)均为实系数多项式,故i z 和j s 只能是实数或共轭复数。
在实际控制系统中,一般闭环极点都不相同,因此一般将输出量的Laplace 变换写为12211()()()(2)mi i q rjk k k j k K s z C s s s sw s w ξ===-=-++∏∏∏ (2-4)式(4)中,q+2r=n,q 为实数极点的个数,r 为共轭复数极点的对数。
在本次设计中,2(),()(48)p K s bG s D s s s s s a+==+++(a=0.01,b=0.011或a=b=20), ()G s H s ⋅()=()p G s 或()G s H s ⋅()=()p G s D (s )。
3 高阶系统零极点分布对系统性能影响分析根轨迹是指当开环系统的某一参数从零变到无穷大时,闭环系统的极点复平面上移动的轨迹。
一般情况下,根轨迹指的是当增益K 由零变到无穷大时根的轨迹。
当高阶系统开环传递函数某一参数发生改变时,利用根轨迹可以很直观的观察出开环零极点对闭环系统特性的影响,并且进行高阶系统各项特性的分析与计算。
借助Matlab 软件,可以利用其中提供的rlocus 函数直接进行系统根轨迹的绘制。
3.1系统开环传递函数为()p G s 的根轨迹当开环传递函数为2()(48)p KG s s s s =++时,在Matlab 中首先构建开环传递 函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下:num=[0,1]; %开环系统传递函数分子 den=[1,4,8,0]; %开环系统传递函数分母 G=tf(num,den); %构建开环系统传递函数 K=[15];rlocus(G) % 直接调用函数画根轨迹图程序运行结果如图3-1所示。
图3-1 ()p G s =2(48)Ks s s ++(k=15)时系统的根轨迹图 3.1.1系统开环传递函数为()p G s ,单位阶跃输入时的根轨迹当系统输入为单位阶跃函数时,输入函数Laplace 变换R(s)= 1/s ,开环传递函数()G s H s ⋅()= ()p G s 或()p G s D (s )。
当开环传递函数为()2G s H s ()(48)p KG s s s s ⋅==++()时,在Matlab 中首先构建开环传递函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下: sys=tf(15,[1 4 8 0]); sysc=feedback(sys,1);step(sysc)程序运行结果如图3-2所示。
图3-2 ()G s H s ⋅()=2(48)Ks s s ++(k=15)单位阶跃响应时系统的根轨迹图3.1.2系统开环传递函数为()p G s ,单位斜坡输入时的根轨迹当系统输入为单位斜坡函数时,r(t)=t,输入函数Laplace 变换R(s)= 21s , 开环传递函数G(s)H(s)= ()p G s =2(48)Ks s s ++,系统均为I 型单位反馈系统。
单位斜坡输入系统稳态误差也被称为速度误差,但并非指系统稳态输出与输入之间存在速度上的误差,而是指系统在斜坡输入作用下,系统输出与输入之间存在位置上的误差。
系统在单位斜坡输入时的根轨迹,具体的程序代码如下:num=[0 0 0 15]; den=[1 4 8 0]; step(num,den,3) grid程序运行结果如图3-3所示图3-3 ()G s H s ⋅()=2(48)Ks s s ++(k=15)单位斜坡响应时系统的根轨迹图 3.1.3动态性能、稳态性能分析稳定是控制系统能够运行的首要条件,在此,分析动态性能时一般以阶跃输入为代表,测定计算系统动态性能,稳态性能分析单位阶跃输入的稳态误差为标准。
单位阶跃输入响应下其动态性能分析如下,如上图2所示可得:上升时间risetime:0.699sec调节时间settingtime:7.65sec峰值peakamplitutd:1.37稳定值final valvue: 1超调量overshoot :36.8 at time:1.83sec稳态误差:0.06253.1.4参考程序法另可采用程序求动态稳态性能,程序如下:G=tf([0 0 0 1], [1 4 8 0]);[y,t]=step(G);C=dcgain(G); %求调节时间setllingtimei =length(t);while(y(i)>0.98*C)&(y(i)<1.02*C)i =i-1;endsetllingtime=t(i)C=dcgain(G); %最大(百分比)超调量percentovershoot [Y,k]=max(y);percentovershoot=100*(Y-C)/C[Y,k]=max(y); %峰值时间( timetopeak )timetopeak=t(k)C=dcgain(G); %上升时间risetimen =1while y(n)<Cn =n+1;endrisetime=t(n)3.2系统开环传递函数为()()p G s D s (a=0.1,b=0.11)的根轨迹当开环传递函数为()p G s D (s )=())1.0)(84(11.02++++s s s s s K 时,在Matlab 中首先 构建开环传递函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下: n=[0 0 0 15 1.65] d=[1 4.1 8.4 0.8 0] rlocus (n,d)程序运行结果如图3-4所示图3-4 ()p G s D (s )=())1.0)(84(11.02++++s s s s s K (k=15)时系统的根轨迹图 3.2.1系统开环传递函数为()()p G s D s ,单位阶跃输入时的根轨迹当开环传递函数为()p G s D (s )=())1.0)(84(11.02++++s s s s s K 时,在Matlab 中首先 构建开环传递函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下:sys=tf([0 0 0 15 1.65], [1 4.1 8.4 0.8 0]); sysc=feedback(sys,1); step(sysc)程序运行结果如图3-5所示图3-5()p G s D (s )=())1.0)(84(11.02++++s s s s s K (k=15)在单位阶跃响应下系统的根轨迹图 3.2.2系统开环传递函数为()()p G s D s ,单位斜坡输入时的根轨迹系统在单位斜坡输入时的根轨迹,具体的程序代码如下:num=[0 0 0 15 1.65];den=[1 4.1 8.4 0.8 0]; step(num,den,3) grid程序运行结果如图3-6所示图3-6()p G s D (s )=())1.0)(84(11.02++++s s s s s K (k=15)在单位斜坡响应下系统的根轨迹图 3.2.3动态性能、稳态性能分析单位阶跃输入响应下其动态性能分析如下,如上图5所示可得: 上升时间risetime : 0.697sec 调节时间settingtime : 7.82sec 峰值 peakamplitutd :1.38 稳定值 final valvue : 1超调量 overshoot : 37.6 at time :1.83sec 稳态误差:0.06673.3系统开环传递函数为()()p G s D s (a =b=20)的根轨迹当开环传递函数为()p G s D (s )=)20)(84()20(2++++s s s s s K 时,在Matlab 中首先 构建开环传递函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下: n=[0 0 0 15 300] d=[1 24 88 160 0] rlocus (n,d)程序运行结果如图3-7所示图3-7 ()p G s D (s )=)20)(84()20(2++++s s s s s K (k=15)时系统的根轨迹图3.3.1系统开环传递函数为()()p G s D s ,单位阶跃输入时的根轨迹当开环传递函数为()p G s D (s )=)20)(84()20(2++++s s s s s K 时,在Matlab 中首先 构建开环传递函数,然后直接调用rlocus 函数精确的绘制系统的根轨迹,具体的程序代码如下:sys=tf([0 0 0 15 300], [1 24 88 160 0]); sysc=feedback(sys,1); step(sysc)程序运行结果如图3-8所示图3-8 ()p G s D (s )=)20)(84()20(2++++s s s s s K (k=15)单位阶跃响应系统的根轨迹图 3.3.2系统开环传递函数为()()p G s D s ,单位斜坡输入时的根轨迹系统在单位斜坡输入时的根轨迹,具体的程序代码如下:num=[0 0 0 15 300]; den=[1 24 88 160 0]; step(num,den,3) grid程序运行结果如图3-9所示图3-9 ()p G s D (s )=)20)(84()20(2++++s s s s s K (k=15)单位斜坡响应系统的根轨迹图 3.3.3动态性能、稳态性能分析单位阶跃输入响应下其动态性能分析如下,如上图8所示可得: 上升时间risetime : 0.699sec 调节时间settingtime : 7.65sec 峰值 peakamplitutd :1.37稳定值final valvue: 1超调量overshoot :36.8 at time:1.83sec 稳态误差:0.06674 分析比较4.1三种仿真结果的比较:表格 1三种情况下的动态性能对照表(1)系统开环传递函数为p 时与系统开环传递函数为p ,a=0.1,b=0.11时较:系统开环传递函数为()()p G s D s ,a=0.1,b=0.11时,系统零点、极点数增加,使得上升时间减小,调节时间增大,超调量增大,稳态误差变大,峰值和峰值时间不变。