连续系统的零极点分析

广东技术师范学院实验报告实验 （三） 项目名称：利用MATLAB 分析连续系统及离散系统的复频域特性一．实验目的1.掌握 Laplace 变换的意义、基本性质及应用。

2.掌握拉普拉斯变换的三维可视化表示。

3.理解系统函数的零、极点分布(极、零图)决定系统时间原函数的特性。

4.掌握系统冲激响应。

5. H (z )部分分式展开的MA TLAB 实现6. H (z )的零极点与系统特性的MATLAB 计算二．实验原理1．Laplace 变换和逆变换定义为⎰⎰∞+∞-∞-==j j stst ds e s F jt f dte tf s F σσπ)(21)()()(0( 4 – 1 )在 Matlab 中实现 Laplace 变换有两个途径：直接调用指令 laplace 和ilaplace 进行；根据定义式 ( 4 – 1 )，利用积分指令 int 实现。

相较而言，直接利用 laplace 和 ilaplace 指令实现机器变换要简洁一些。

调用格式：L=laplace(F) F=ilaplace(L)2．实现拉普拉斯曲面图及其可视化的步骤如下：a ．定义两个向量x 和y 来确定绘制曲面图的复平面横座标和纵座标的范围。

b ．调用meshgrid 函数产生包含绘制曲面图的s 平面区域所有等间隔取样点的复矩阵。

c ．计算复矩阵s 定义的各样点处信号拉氏变换F(s)的函数值，并调用abs 函数求其模。

d ．调用mesh 函数绘出其幅度曲面图。

3．在连续系统的复频域分析中，系统函数起着十分重要的作用，它包含了连续系统的固有特性。

通过系统函数可以对系统的稳定性、时域特性、系统频率响应等系统特性进行分析。

若连续系统的系统函数的零极点已知，系统函数便可确定下来，即系统函数H （s ）的零极点分布完全决定了系统的特性。

系统函数的零点和极点位置可以用matlab 的多项式求根函数roots()来求得。

用roots()函数求得系统函数H(s)的零极点后，就可以用plot 命令在复平面上绘制出系统函数的零极点图。

极点对系统性能影响一．控制系统与极点自动控制系统根据控制作用可分为：连续控制系统和采样控制系统，采样系统又叫离散控制系统。

通常把系统中的离散信号是脉冲序列形成的离散系统,称为采样控制系统。

连续控制系统即指控制量为连续的模拟量如时变系统。

系统的数学模型一般由系统传递函数表达。

传递函数为零初始条件下线性系统响应（即输出）量的拉普拉斯变换（或z 变换）与激励（即输入）量的拉普拉斯变换之比。

记作Φ（s ）=Xo （s ）/Xi （s ），其中Xo （s ）、Xi （s ）分别为输出量和输入量的拉普拉斯变换。

特征方程的根称为极点。

如试Φ﹙S ﹚= C [∏（S-Pi ）/∏(S-Qi) ]中Q1 Q2 Q3 …… Qi ……即为系统的极点。

二．极点对系统的影响极点--确定了系统的运动模态；决定了系统的稳定性。

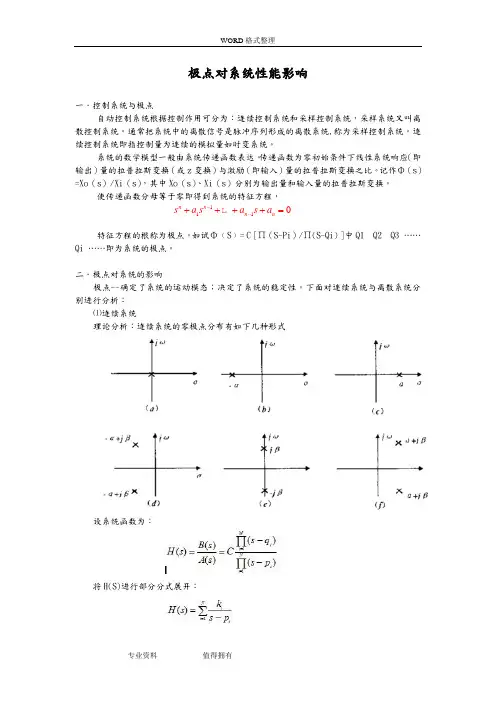
下面对连续系统与离散系统分别进行分析：⑴连续系统理论分析：连续系统的零极点分布有如下几种形式设系统函数为：将H(S)进行部分分式展开：1n a s -+++系统冲激响应H(S)的时域特性h(t)随时间衰减的信号分量完全由系统函数H(S)的极点位置决定。

每一个极点将决定h(t)的一项时间函数。

稳定性：由上述得知Y(S)= C [∏（S-Pi ）/(S-Qi) ]可分解为Y(S)=C1/(S-τ1)+ C2/(S-τ2)+ C3/(S-τ3)+……+ Ci/(S-τi)+…… 则时间响应为……由于特征方程的根不止一个，这时，应把系统的运动看成是多个运动分量的合成。

只要有一个运动分量是发散的，则系统是不稳定的。

因此，特征方程所有根的实部都必须是负数，亦即所有的根都在复平面的左半平面。

通过复变函数幅角定理将S 由G 平面映射到GH 平面。

如果封闭曲线 F 内有Z 个F(s)的零点，有P 个F(s)的极点，则s 沿 F 顺时针转一圈时，在F(s)平面上，F(s)曲线绕原点顺时针转的圈数R 为z 和p 之差，即R ＝z －p 。

极点对系统性能影响一．控制系统与极点自动控制系统根据控制作用可分为：连续控制系统和采样控制系统，采样系统又叫离散控制系统。

通常把系统中的离散信号是脉冲序列形成的离散系统,称为采样控制系统。

连续控制系统即指控制量为连续的模拟量如时变系统。

系统的数学模型一般由系统传递函数表达。

传递函数为零初始条件下线性系统响应（即输出）量的拉普拉斯变换（或z 变换）与激励（即输入）量的拉普拉斯变换之比。

记作Φ（s ）=Xo （s ）/Xi （s ），其中Xo （s ）、Xi （s ）分别为输出量和输入量的拉普拉斯变换。

特征方程的根称为极点。

如试Φ﹙S ﹚= C [∏（S-Pi ）/∏(S-Qi) ]中Q1 Q2 Q3 …… Qi ……即为系统的极点。

二．极点对系统的影响极点--确定了系统的运动模态；决定了系统的稳定性。

下面对连续系统与离散系统分别进行分析：⑴连续系统理论分析：连续系统的零极点分布有如下几种形式设系统函数为：将H(S)进行部分分式展开：1n a s -+++系统冲激响应H(S)的时域特性h(t)随时间衰减的信号分量完全由系统函数H(S)的极点位置决定。

每一个极点将决定h(t)的一项时间函数。

稳定性：由上述得知Y(S)= C [∏（S-Pi ）/(S-Qi) ]可分解为Y(S)=C1/(S-τ1)+ C2/(S-τ2)+ C3/(S-τ3)+……+ Ci/(S-τi)+…… 则时间响应为……由于特征方程的根不止一个，这时，应把系统的运动看成是多个运动分量的合成。

只要有一个运动分量是发散的，则系统是不稳定的。

因此，特征方程所有根的实部都必须是负数，亦即所有的根都在复平面的左半平面。

通过复变函数幅角定理将S 由G 平面映射到GH 平面。

如果封闭曲线 F 内有Z 个F(s)的零点，有P 个F(s)的极点，则s 沿 F 顺时针转一圈时，在F(s)平面上，F(s)曲线绕原点顺时针转的圈数R 为z 和p 之差，即R ＝z －p 。

信号与系统分析一、典型信号的matlab 表示表示连续信号，需定义自变量的范围和取样间隔，如t=0:0.01:3 1. 实指数信号 y=k*exp(a*t)2. 正弦信号 k*sin(w*t+phi) k*cos(w*t+phi)3. 复指数信号 y=k*exp((a+i*b)*t)实部real(y) 虚部imag(y) 模abs(y) 相角angle(y) 共轭conj(y) 4. 抽样信号 Sat=sinc(t/pi)5. 矩形脉冲信号 y=rectpuls(t,width)周期方波信号 y=square(2*pi*f*t,duty) %产生频率为fHZ ，占空比为duty%的方波 6. 三角脉冲信号非周期三角波y=tripuls(t,width,skew) %斜度 skew ，最大幅度出现在t=(width/2)*skew 周期三角波 y=sawtooth(t,width)7. 单位阶跃信号 function y=uCT(t) y=(t>=0)阶跃信号符号函数 Heaviside() y=sym(‘Heaviside(t)’) %调用时必须用sym 定义 冲激信号符号函数 Dirac()二、Matlab 的符号运算 1. 定义符号变量syms 变量名 syms xsym(‘变量名’) x=sym(‘x ’) sym(‘表达式’) sym(‘x+1’)2. 化简符号运算结果 simple 或simplify3. 绘制符号表达式图形 ezplot(y,[a,b])三、连续信号的运算微分和积分运算（用符号表达式来表示） 1. 微分运算Diff(function,’variable ’,n) % variable 为求导变量，n 为求导阶数 例：syms a x y y=sin(a*x^2); dy=diff(y ,’x ’) 2. 积分运算int(function, ’variable ’,a,b) %a 为积分下限，b 为积分上限 3. 信号的反折 fliplr(x) 4. 卷积计算1） 符号运算计算卷积（求解积分的方法） 例：)(*)()(t u e t u et y tTt --=syms T t taoxt1=exp(-t); xt2=exp(-t/T);xt_tao=subs(xt1,t,tao)*subs(xt2,t,t-tao);yt=int(xt_tao,tao,0,t); yt=simplify(yt);2) 数值计算法求卷积 conv( )y = dt*conv(e,h)例：求e(t) = u(t)-u(t-1)和h(t) = u(t)-u(t-1)的卷积 t0 = -2; t1 = 4; dt = 0.01; t = t0:dt:t1; e = u(t)-u(t-1); h = u(t)-u(t-1);y = dt*conv(e,h); % Compute the convolution of x(t) and h(t) subplot(221)plot(t,e), grid on, title('Signal e(t)'), axis([t0,t1,-0.2,1.2]) subplot(222)plot(t,h), grid on, title('Signal h(t)'), axis([t0,t1,-0.2,1.2]) subplot(212)t = 2*t0:dt:2*t1; % the time range to the convolution of e and h.plot(t,y), grid on, title('The convolution of x(t) and h(t)'), axis([2*t0,2*t1,-0.1,1.2]), xlabel('Time t sec')四、连续LTI 系统的时域分析1. 系统响应的符号求解 dsolve(‘eq1,eq2,…’,’cond1,cond2,…’); %eqi 表示微分方程，condi 表示初始条件 例：eq=’D3y+2*D2y+Dy=0’;cond=’y(0)=1,Dy(0)=1,D2y(0)=2’; yzi=dsolve(eq,cond); %零输入响应 simplify(yzi);eq1=’D3y+4*D2y+8*Dy=3*Dx+8*x ’; eq2=’x=Heaviside(t)’;cond=’y(-0.01)=0,Dy(-0.01)= 0,D2y(-0.01)=0’; yzs=dsolve(eq1,eq2,cond);simplify(yzs.y); %零状态响应2. 零状态响应的数值求解1）y=lsim(sys,f,t)%sys 表示系统模型，由sys=tf(b,a)生成的系统函数对象 %f 输入信号向量，t 时间抽样点向量例：)()sin()(),()()()('''t u t t f t f t y t y t y π210665==++ ts=0;te=5;dt=0.01; sys=tf([6],[1,5,6]); t=ts:dt:te;f=10*sin(2*pi*t).*UT(t);y=lsim(sys,f,t);plot(t,y),grid on;xlabel(‘time ’),ylabel(‘y(t)’); title(‘零状态响应’); 2）y=conv(f,impul)3. 连续系统冲激响应 y=impulse(sys,t) %sys 表示系统模型4. 连续系统阶跃响应 y=step(sys,t)五、信号的频域分析 1.傅立叶变换 1）符号运算求法 fourier( )和ifourier( )例：)()(t u e t f t 2-=的傅立叶变换ft=sym(‘exp(-2*t)*Heaviside(t)’); fw=fourier(ft)ezplot(abs(fw)); %或者fw_conj=conj(fw);Gw=sqrt(fw*fw_conj); phase=atan(image(fw)/real(fw));%或者angle(fw) ezplot(phase)211Ω+=Ω)(j F 的傅立叶反变换syms tfw=sym(‘1/(1+w^2’); ft=ifourier(fw,t) 2）数值计算求法[][][]Nk k N en f k F k TN M n j TM TN k ≤≤∆=∆∆=-⨯-∆--⨯-⨯02111111,)()()()()()(πωω例：求)(t G 82的傅立叶变换 1)数值计算dt=0.01; t=-4:dt:4;ft=(t+4)/2.*uCT(t+4)-t.*uCT(t)+(t-4)/2.*uCT(t-4); N=2000; k=-N:N;W=pi*k/(N*dt);F=dt*ft*exp(-j*t'*W); F=abs(F); plot(W,F),grid on; axis([-pi pi -1 9]);title('amplitude spectrum'); 2）符号计算ft=sym('(t+4)/2*Heaviside(t+4)-t*Heaviside(t)+(t-4)/2*Heaviside(t-4)'); Fw=simplify(fourier(ft));ezplot(abs(Fw),[-pi pi]);grid on;2. 系统的频率特性1) [H,w] = freqs(b,a)：连续系统频率响应的函数2) 波特图：采用对数坐标的幅频特性和相频特性曲线,可显示频响间的微小差异 bode(sys)例：求11+=s s H )(的频率特性w=0:0.01:8*pi; b=[1]; a=[1 1]; H=freqs(b,a,w); subplot(211); plot(w,abs(H)); subplot(212); plot(w,angle(H)); figure(2); sys=tf(b,a); bode(sys);3. 连续时间LTI 系统的频域分析 例:551+Ω=Ω--=j j H t u t u t x )(),()()(，求系统的响应。

《信号与系统》实验报告姓名：学号：同组人：无指导教师：成绩：实验一典型连续时间信号描述及运算实验报告要求：（1）仿照单边指数信号的示例程序，按要求完成三种典型连续信号，即：正弦信号、衰减正弦信号、钟型信号的波形绘制。

（要求：要附上程序代码，以下均如此，不再说明）（2）根据《信号与系统》教材第一章的习题1.1（1，3，5，8）函数形式绘制波形。

（3）完成三种奇异信号，即：符号函数、阶跃信号、单位冲激信号的波形绘制。

（4）完成实验一中信号的运算：三、6 实验内容中的（1）（2）（3）（4）。

（5）求解信号的直流/交流分量，按第四部分的要求完成。

正文：（1）<1>正弦信号：代码：>> t=-250:1:250;>> f1=150*sin(2*pi*t/100);>> f2=150*sin(2*pi*t/200);>> f3=150*sin(2*pi*t/200+pi/5);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.')<2>衰减正弦信号<3>代码：>> t=-250:1:250;>> f1=400*exp(-1.*t.*t./10000);>> f1=400*exp(-1.*t.*t./22500);>> f1=400*exp(-1.*t.*t./62500);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.') (2)习题1，3，5，8<1>代码：t=0:1:10;f=t;plot(t,f)<3>代码：t=1:1:10;f=t;plot(t,f)<5>代码：t=0:1:10;f=2-exp(-1.*t.);plot(t,f)<8>代码：t=1:0.1:2;f=exp(-1.*t.)*cos(10*pi*t);plot(t,f)(3)三种奇异函数<1>符号函数代码: t=-5:0.05:5;f=sign(t);plot(t,f)<2>阶跃信号代码:>> t=-5:0.1:5;>> f=u(t);>> plot(t,f)<3>单位冲激信号代码：function chongji(t1,t2,t0)dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt]) title('单位冲激信号δ(t) ')（4）实验三1234<1>syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,2,1);ezplot(f1);y1=subs(f1,t,-t);f3=f1+y1;subplot(1,2,2);ezplot(f3);function f=u(t) f=(t>0);<2>4、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,3,1);ezplot(f1);f2=sym('sin(2*pi*t)');subplot(1,3,2);ezplot(f2);f6=f1.*f2;subplot(1,3,3);ezplot(f6);5、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); f2=sym('sin(2*pi*t)');subplot(1,3,1);ezplot(f2);f6=f1.*f2;y6=subs(f6,t,t-2);subplot(1,3,2);ezplot(y6);f7=y6+f2;subplot(1,3,3);ezplot(f7);四、t=0:0.1:500;f=100.*abs(sin(2.*pi.*t./50)); plot(t,f,t,fD,t,fA)调用子程序：function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;(5)求解信号的交直流分量代码：function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;t=0:0.1:500;f(t)=100|sin(2*PI*t/50)|;plot(t,fD,t,fA)实验二线性系统时域分析实验报告要求：（1）求解下面两个信号的卷积积分。

实验Z变换、零极点分析1. 学会运⽤MATLAB 求离散时间信号的z 变换和z 反变换；⼀、实验原理及实例分析（⼀）离散时间信号的Z 变换1．利⽤MATLAB 实现z 域的部分分式展开式MATLAB 的信号处理⼯具箱提供了⼀个对F(Z)进⾏部分分式展开的函数residuez()，其调⽤形式为：[r,p,k]=residuez(num,den)式中，num 和den 分别为F(Z)的分⼦多项式和分母多项式的系数向量，r 为部分分式的系数向量，p 为极点向量，k 为多项式的系数向量。

【实例1】利⽤MATLAB 计算321431818)(-----+zz z z F 的部分分式展开式。

解：利⽤MATLAB 计算部分分式展开式程序为% 部分分式展开式的实现程序num=[18];den=[18 3 -4 -1];[r,p,k]=residuez(num,den)2．Z 变换和Z 反变换MATLAB 的符号数学⼯具箱提供了计算Z 变换的函数ztrans()和Z 反变换的函数iztrans （），其调⽤形式为)()(F iztrans f f ztrans F ==上⾯两式中，右端的f 和F 分别为时域表⽰式和z 域表⽰式的符号表⽰，可应⽤函数sym 来实现，其调⽤格式为()A sym S =的Z 反变换。

解（1）Z 变换的MATLAB 程序% Z 变换的程序实现f=sym('a^n');F=ztrans(f)程序运⾏结果为：z/a/(z/a-1)可以⽤simplify( )化简得到 :-z/(-z+a)（2）Z 反变换的MATLAB 程序% Z 反变换实现程序F=sym('a*z/(z-a)^2');f=iztrans(F)程序运⾏结果为f =a^n*n（⼆）系统函数的零极点分析1. 系统函数的零极点分布离散时间系统的系统函数定义为系统零状态响应的z 变换与激励的z 变换之⽐，即)()()(z X z Y z H = （3-1）如果系统函数)(z H 的有理函数表⽰式为：11211121)(+-+-++++++++=n n n n m m m m a z a z a z a b z b z b z b z H （3-2）那么，在MATLAB 中系统函数的零极点就可通过函数roots 得到，也可借助函数tf2zp 得到，tf2zp 的语句格式为：[Z,P,K]=tf2zp(B,A)其中，B 与A 分别表⽰)(z H 的分⼦与分母多项式的系数向量。

信号与系统实验报告连续线性时不变系统的分析专业：电子信息工程（实验班）姓名：曾雄学号：14122222203班级：电实12-1BF目录一、实验原理与目的 (3)二、实验过程及结果测试 (3)三、思考题 (10)四、实验总结 (10)五、参考文献 (11)一、实验原理与目的深刻理解连续时间系统的系统函数在分析连续系统的时域特性、频域特性及稳定性中的重要作用及意义。

掌握利用MATLAB 分析连续系统的时域响应、频响特性和零极点的基本方法。

二、实验过程及结果测试1．描述某线性时不变系统的微分方程为： ''()3'()2()'()y t y t y t f t f t++=+ 且f(t)=t 2，y(0-)=1，y ’(0-)=1；试求系统的单位冲激响应、单位阶跃响应、全响应、零状态响应、零输入响应、自由响应和强迫响应。

编写相应MATLAB 程序，画出各波形图。

（1）单位冲激响应： 程序如下：%求单位冲激响应a=[1,3,2]; b=[1,2]; sys=tf(b,a); t=0:0.01:10; h=impulse(sys,t);%用画图函数plot( )画单位冲激响应的波形plot(h); %单位冲激响应曲线 xlabel('t'); ylabel('h');title('单位冲激响应h(t)') 程序运行所得波形如图一：200400600800100012000.10.20.30.40.50.60.70.80.91th单位冲激响应h(t )图一 单位冲激响应的波形（2）单位阶跃响应： 程序如下：%求单位阶跃响应a=[1,3,2]; b=[1,2]; sys=tf(b,a); t=0:0.01:10; G=step(sys,t);%用画图函数plot( )画单位阶跃响应的波形plot(G); %单位阶跃响应曲线 xlabel('t'); ylabel('g');title('单位阶跃响应g(t)') 程序运行所得波形如图二：2004006008001000120000.10.20.30.40.50.60.70.80.91tg单位阶跃响应g(t )图二 单位阶跃响应的波形 （3）零状态响应： 程序如下：%求零状态响应yzs=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0') %用符号画图函数ezplot( )画各种响应的波形 t=0:0.01:3;ezplot(yzs,t); %零状态响应曲线 axis([0,3,-1 5]);title('零状态响应曲线yzs'); ylabel('yzs');程序运行所得波形如图三：00.511.522.53-112345t零状态响应曲线yzsy z s图三 零状态响应的波形（4）零输入响应： 程序如下：%求零输入响应yzi=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1') %用符号画图函数ezplot( )画零输入响应的波形 t=0:0.01:3;ezplot(yzi,t);%零输入响应曲线 axis([0,3,-1,2]); title('零输入响应yzi'); ylabel('yzi');程序运行所得波形如图四：图四 零输入响应的波形（5）全响应：程序如下：%求全响应y=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=1,Dy(0)=1') %用符号画图函数ezplot( )画全响应响应的波形00.511.522.53-1-0.50.511.52t零输入响应yziy z it=0:0.01:3;ezplot(y,t); %全响应曲线 axis([0,3,-1,5]); title('全响应y'); ylabel('y');程序运行所得波形如图五：00.511.522.53-112345t全响应yy图五 全响应的波形（6）自由响应：程序如下：%自由响应y=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=1,Dy(0)=1'); %全响应 yht=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1'); % 求齐次通解yt=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0'); % 求非齐次通解 yp=yt-yht;yh=y-yp; % 求齐次解，即自由响应 t=0:0.01:3; ezplot(yh,t); title('自由响应yh'); ylabel('yh');程序运行所得波形如图六：0.511.522.530.511.52t自由响应yhy h图六 自由响应的波形（7）强迫响应： 程序如下：%强迫响应yht=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1'); % 求齐次通解yt=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0'); % 求非齐次通解 yp=yt-yht; % 求特解，即强迫响应 t=0:0.01:3; ezplot(yp,t); title('强迫响应yp'); ylabel('yp');程序运行所得波形如图七：0.511.522.53-112345t强迫响应ypy p图七 强迫响应的波形2．给定一个连续线性时不变系统，描述其输入输出之间关系的微分方程为：编写MATLAB 程序，绘制系统的幅频响应、相频响应、频率响应的实部和频率响应的虚部的波形，确定滤波器的类型。

∞连续系统零极点分析理论基础根据系统函数 H (s ) 的零极点分布来分析连续系统的稳定性是零极点分析的重要应用之一。

稳定性是系统固有的性质，与激励信号无关，由于系统函数 H (s ) 包含了系统的所有固有特性，显然它也能反映出系统是否稳定。

对任意有界信号 f (t )，若系统产生的零状态响应 y (t ) 也是有界的，则称该系统为稳定系统，否则，则称为不稳定系统。

上述稳定性的定义可以等效为下列条件：● 时域条件：连续系统稳定充要条件为⎰-∞ h (t ) dt < ∞ ，即冲激响应绝对可积；● 复频域条件：连续系统稳定的充要条件为系统函数 H (s ) 的所有极点位于S 平面的左半平面。

系统稳定的时域条件和频域条件是等价的。

因此，只要考察系统函数 H (s ) 的极点分布，就可判断系统的稳定性。

对于三阶以下的低阶系统，可以利用求根公式方便地求出极点位置，从而判断系统稳定性。

第一小题 A=[3 5 4 6];B=[1 1 2];p=roots(A);q=roots(B);p=p';q=q';x=max(abs([p q 1]));x=x+0.1;y=x;clf;hold on ;axis([-x x -y y]) ;axis('square');figure(1);plot([-x x],[0 0]) ;title("零极点分布图");plot([0 0],[-y y]) ;plot(real(p),imag(p),'x') ;plot(real(q),imag(q),'o') ;hold off ;f1=0;f2=2;k=0.01;p=p';q=q';f=f1:k:f2; %定义绘制系统频率响应曲线的频率范围w=f*(2*pi);y=1i*w;n=length(p);m=length(q);if n==0 %如果系统无极点yq=ones(m,1)*y;vq=yq-q*ones(1,length(w));bj=abs(vq);cosaij=angle(vq)./pi.*180;61;ai=1;thetai=0;elseif m==0 %如果系统无零点yp=ones(n,1)*y;vp=yp-p*ones(1,length(w));ai=abs(vp);thetai=angle(vp)./pi.*180;bj=1;cosaij=0;elseyp=ones(n,1)*y;yq=ones(m,1)*y;vp=yp-p*ones(1,length(w));vq=yq-q*ones(1,length(w));ai=abs(vp);thetai=angle(vp)./pi.*180;bj=abs(vq);cosaij=angle(vq)./pi.*180;endfigure(2);Hw=prod(bj,1)./prod(ai,1);plot(f,Hw);title('连续系统幅频响应曲线')xlabel('频率 w（单位：赫兹） ')ylabel('F(jw)')figure(3);Angw=sum(cosaij,1)-sum(thetai,1);plot(f,Angw);title('连续系统相频响应曲线')xlabel('频率 w（单位：赫兹） ')ylabel('Angle(jw)')第四小题A=[1 2 2 1];B=[1];p=roots(A);q=roots(B);p=p';q=q';x=max(abs([p q 1])); x=x+0.1;y=x;clf;hold on;axis([-x x -y y]) ; axis('square');figure(1);plot([-x x],[0 0]) ;title("零极点分布图"); plot([0 0],[-y y]) ;plot(real(p),imag(p),'x') ;plot(real(q),imag(q),'o') ;hold off;f1=0;f2=2;k=0.01;p=p';q=q';f=f1:k:f2; %定义绘制系统频率响应曲线的频率范围w=f*(2*pi);y=1i*w;n=length(p);m=length(q);if n==0 %如果系统无极点yq=ones(m,1)*y;vq=yq-q*ones(1,length(w));bj=abs(vq);cosaij=angle(vq)./pi.*180;61;ai=1;thetai=0;elseif m==0 %如果系统无零点yp=ones(n,1)*y;vp=yp-p*ones(1,length(w));ai=abs(vp);thetai=angle(vp)./pi.*180;bj=1;cosaij=0;elseyp=ones(n,1)*y;yq=ones(m,1)*y;vp=yp-p*ones(1,length(w));vq=yq-q*ones(1,length(w));ai=abs(vp);thetai=angle(vp)./pi.*180;bj=abs(vq);cosaij=angle(vq)./pi.*180;endfigure(2);Hw=prod(bj,1)./prod(ai,1);plot(f,Hw);title('连续系统幅频响应曲线')xlabel('频率 w（单位：赫兹） ') ylabel('F(jw)')figure(3);Angw=sum(cosaij,1)-sum(thetai,1); plot(f,Angw);title('连续系统相频响应曲线') xlabel('频率 w（单位：赫兹） ') ylabel('Angle(jw)')。

信号与系统实验报告——连续时间系统的复频域分析班级：05911101学号：**********姓名：***实验五连续时间系统的复频域分析——1120111487 信息工程（实验班）蒋志科一、实验目的①掌握拉普拉斯变换及其反变换的定义，并掌握MA TLAB 实现方法 ②学习和掌握连续时间系统系统函数的定义及其复频域分析方法③掌握系统零极点的定义，加深理解系统零极点分布与系统特性的关系。

二、实验原理与方法 1、拉普拉斯变换连续时间信号x(t)的拉普拉斯变换定义为：X s =x (t )e −st dt +∞−∞拉普拉斯反变换为：x t =12πj X (s )e st ds σ+j ∞σ−j ∞在MA TLAB 中可以采用符号数学工具箱中的laplace 函数和ilaplace 函数进行拉氏变换和拉氏反变换。

L=laplace(F)符号表达式F 的拉氏变换，F 中时间变量为t ，返回变量为s 的结果表达式。

L=laplace(F,t)用t 替换结果中的变量s 。

F=ilaplace(L)以s 为变量的符号表达式L 的拉氏反变换，返回时间变量t 的结果表达式。

F=ilaplace(L,x)用x 替换结果中的变量t 。

2、连续时间系统的系统函数连续时间系统的系统函数是系统单位冲激响应的拉氏变换H s =ℎ(t )e −st dt +∞−∞此外，连续时间系统的系统函数还可以由系统输入和输出信号的拉氏变换之比得到H s =Y(s)/X(s) 单位冲激响应h(t)反映了系统的固有性质，而H(s)从复频域反映了系统的固有性质。

对于H(s)描述的连续时间系统，其系统函数s 的有理函数H s =b M s M +b M−1s M−1+⋯+b 0a n s n +a n −1s M−1+⋯+a 03、连续时间系统的零极点分析系统的零点指使式H s 的分子多项式为零的点，极点指使分母多项式为零的点，零点使系统的值为零，极点使系统函数的值无穷大。

信号与系统实验陈述课程名称：信号与系统实验实验项目名称：连续线性时不变系统分析专业班级：姓名：学号：完成时间：年月日一、实验目的1．掌握连续LTI系统的单位冲激响应、单位阶跃响应和任意激励对应响应的求解方法。

2．掌握连续LTI系统的频域分析方法。

3．掌握连续LTI系统的复频域分析方法。

4．掌握连续LTI系统的时域、频域和复频域分析方法的相互转换。

二、实验原理1．连续LTI系统的时域分析(1)连续线性时不变系统的描述设连续线性时不变系统的激励为，响应为，则描述系统的微分方程可暗示为为了在Matlab编程中调用有关函数，我们可以用向量和来暗示该系统，即这里要注意，向量和的元素排列是按微分方程的微分阶次降幂排列，缺项要用0补齐。

(2) 单位冲激响应单位冲激响应是指连续LTI系统在单位冲激信号激励下的零状态响应，因此满足线性常系数微分方程(5.1)及零初始状态，即，依照定义，它也可暗示为对于连续LTI系统，若其输入信号为，冲激响应为，则其零状态响应为可见，能够刻画和表征系统的固有特性，与何种激励无关。

一旦知道了系统的冲激响应，就可求得系统对任何输入信号所发生的零状态响应。

Matlab提供了专门用于求连续系统冲激响应的函数impulse()，该函数还能绘制其时域波形。

(3)单位阶跃响应单位阶跃响应是指连续LTI系统在单位阶跃信号激励下的零状态响应，它可以暗示为Matlab提供了专门用于求连续系统单位阶跃响应的函数step( )，该函数还能绘制其时域波形。

(4)任意激励下的零状态响应已经知道，连续LTI系统可用常系数线性微分方程(5.1)式来描述，Matlab提供的函数lsim( )能对上述微分方程描述的连续LTI系统的响应进行仿真，该函数不但能绘制指定时间范围内的系统响应波形图，而且还能求出系统响应的数值解。

其调用格式有lsim(b,a,x,t)y=lsim(b,a,x,t) ：只求出系统的零状态响应的数值解，而不绘制响应曲线需要特别强调的是，Matlab总是把由分子和分母多项式暗示任何系统都当作是因果系统。

目录1.引言 (2)2.虚拟仪器开发软件Labview入门 (3)2.1 Labview简介 (3)2.2 利用Labview编程完成习题设计 (3)3.利用LabVIEW实现系统函数的零极点分布决定时域特性的设计 (20)3.1系统函数的零极点分布决定时域特性的基本原理 (20)3.2系统函数的零极点分布决定时域特性的编程设计及实现 (22)3.3运行结果及分析 (23)4. 总结 (25)5.参考文献 (25)1.引言冲激响应h(t)与系统函数H(s) 从时域和变换域两方面表征了同一系统的本性。

在s 域分析中，借助系统函数在s平面零点与极点分布的研究，可以简明、直观地给出系统响应的许多规律。

系统的时域、频域特性集中地以其系统函数的零、极点分布表现出来。

主要优点：可以预言系统的时域特性；便于划分系统的各个分量（自由／强迫，瞬态／稳态）；可以用来说明系统的正弦稳态特性。

2.虚拟仪器开发软件Labview入门2.1 Labview简介LabVIEW是一种程序开发环境，由美国国家仪器（NI）公司研制开发的，类似于C 和BASIC开发环境，但是LabVIEW与其他计算机语言的显著区别是：其他计算机语言都是采用基于文本的语言产生代码，而LabVIEW使用的是图形化编辑语言G编写程序，产生的程序是框图的形式。

LabVIEW（Laboratory Virtual Instrument Engineering Workbench）是一种用图标代替文本行创建应用程序的图形化编程语言。

传统文本编程语言根据语句和指令的先后顺序决定程序执行顺序，LabVIEW 则采用数据流编程方式，程序框图中节点之间的数据流向决定VI及函数的执行顺序。

VI指虚拟仪器，是LabVIEW]的程序模块。

LabVIEW 提供很多外观与传统仪器（如示波器、万用表）类似的控件，可用来方便地创建用户界面。

用户界面在LabVIEW中被称为前面板。

使用图标和连线，可以通过编程对前面板上的对象进行控制。