零极点分布

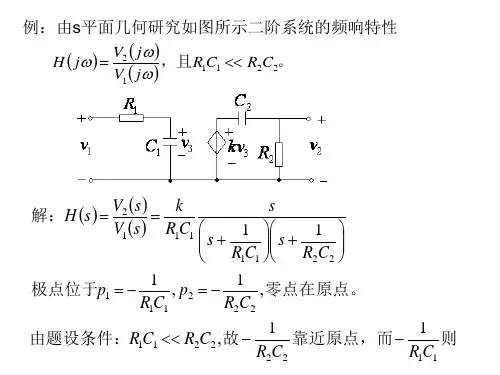
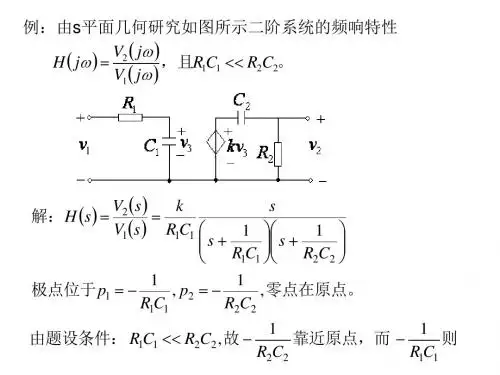
零极点分布与增益曲线零极点分布和增益曲线是表征连续时间线性非时变（LTI）系统的重要工具。

它们提供有关系统频率响应、稳定性和其他特性的宝贵见解。

零点零点是传递函数分母多项式根的倒数。

它们对应于系统频率响应中的无限增益点。

零点分布决定了增益曲线的形状和整体响应。

极点极点是传递函数分子多项式根的倒数。

它们对应于系统频率响应中的零增益点。

极点分布决定了系统的稳定性和阻尼特性。

增益曲线增益曲线是系统频率响应的幅度-频率图。

它表示系统输出信号相对于输入信号幅度的变化。

增益曲线受零极点分布的影响。

零极点分布的影响零极点分布对增益曲线和系统性能有以下影响：共振峰：零点靠近极点会导致增益曲线出现共振峰。

峰值频率由零点和极点的相对位置决定。

带宽：零点和极点之间的距离决定了系统的带宽。

带宽较宽的系统响应频率范围较广。

相位裕度：零极点分布影响系统的相位裕度。

相位裕度是系统稳定性的度量，由极点和零点的相对位置决定。

增益曲线的特征增益曲线的关键特征包括：增益幅度：增益幅度是增益曲线的峰值或最大值。

截止频率：截止频率是增益曲线下降到特定值（通常为 3 dB）的频率。

共振频率：共振频率是增益曲线上共振峰发生的频率。

带宽：带宽是增益曲线高于特定值（通常为 3 dB）的频率范围。

系统稳定性零极点分布对于系统的稳定性至关重要。

系统稳定当且仅当所有极点的实部为负。

应用零极点分布和增益曲线在许多领域有广泛的应用，包括：控制系统设计滤波器设计信号处理通信系统通过理解零极点分布和增益曲线之间的关系，工程师可以优化系统性能以满足特定要求。

离散系统的频率响应分析和零极点分布离散系统的幅频响应描述了系统对不同频率信号的放大或压缩能力。

幅频响应一般用幅度响应曲线表示，即以输入信号频率为横轴，以输出信号幅度为纵轴绘制的曲线。

幅频响应曲线可以展示离散系统的增益特性，即在不同频率下系统对信号的放大或压缩程度。

幅频响应曲线上的波动和变化可以反映系统对不同频率信号的响应情况。

离散系统的相频响应描述了系统对不同频率信号的相位差。

相频响应也是以输入信号频率为横轴，以输出信号相位为纵轴绘制的曲线。

相频响应可以展示离散系统对不同频率信号的相位延迟或提前情况，即输入信号和输出信号之间的相位差。

相频响应的变化可以反映系统对不同频率信号相位的变化情况。

在频率响应分析中，零极点分布也是非常重要的。

零点是指离散系统传递函数的分子多项式为零的根，极点是指传递函数的分母多项式为零的根。

零极点的分布对离散系统的频率响应和系统特性有着重要的影响。

具体来说，零点会在幅频响应曲线上产生波动或峰值，影响系统的放大或压缩程度。

零点的频率越高，波动或峰值的位置越靠近高频，反之亦然。

而极点会导致幅频响应曲线的趋势变化，影响系统的稳定性和阻尼特性。

极点越接近单位圆，系统越不稳定；极点越远离单位圆，系统越稳定。

相频响应同样受到零点和极点的影响。

零点的频率越高，在相频响应曲线上引起的相位变化越明显。

而极点的频率越接近单位圆，相频响应曲线呈现明显的相位延迟。

极点越远离单位圆，相频响应曲线呈现相位提前的情况。

因此，频率响应分析和零极点分布是研究离散系统特性的重要方法。

通过频率响应分析和零极点分布，我们可以了解离散系统对不同频率输入信号的响应情况、系统的稳定性特点以及系统的放大和压缩能力。

这对于离散系统的设计、控制和优化都有着重要的指导意义。

二、实验项目名称：离散系统的转移函数，零、极点分布和模拟 三、实验原理：离散系统的时域方程为∑∑==-=-Mm m Nk km n x b k n y a][][其变换域分析方法如下：系统的频率响应为 ωωωωωωωjN N j jM M j j j j ea e a a eb e b b e A e B e H ----++++++==......)()()(1010 Z 域 )()()(][][][][][z H z X z Y m n h m x n h n x n y m =⇔-=*=∑∞-∞=系统的转移函数为 NN MM z a z a a z b z b b z A z B z H ----++++++==......)()()(110110 分解因式 ∏∏∑∑=-=-=-=---==Ni i Mi i N i i kMi ik z z Kz a zb z H 11110)1()1()(λξ ，其中i ξ和i λ称为零、极点。

在MATLAB 中，可以用函数[z,p,K]=tf2zp （num,den ）求得有理分式形式的系统转移函数的零、极点，用函数zplane （z ，p ）绘出零、极点分布图；也可以用函数zplane （num ，den ）直接绘出有理分式形式的系统转移函数的零、极点分布图。

四、实验目的：1、加深对离散系统转移函数、零极点概念的理解；2、根据系统转移函数求系统零极点分布。

五、实验内容：实验内容（一）、使用实验仿真系统(略) 实验内容（二）、MATLAB 仿真六、实验器材（设备、元器件）：计算机、MATLAB 软件。

七、实验步骤：对系统系统2181.09.011)(--+-=zz z H1、编程实现系统的参数输入，绘出幅度频率响应曲线和零、极点分布图。

2、根据系统的零极点计算系统频率响应的幅值和相位。

定义omega=[0:511]*pi/256和unitcirc=exp(j*omega)得到在单位圆上512个等分点，在这些点上将要对频率响应)(jw e H 求值。

离散系统的频域分析与零极点分布Ⅱ离散系统的频域分析是对离散系统在频域上的特性进行分析和研究。

频域分析的基本思想是将离散系统的输入输出关系表示为频率响应函数的形式，通过频率响应函数来描述离散系统的特性。

而离散系统的零极点分布则是分析离散系统的传递函数的零点和极点在复平面上的分布情况，对于离散系统的稳定性和频率响应特性有着重要的影响。

首先，我们来讨论离散系统的频域分析。

离散系统的频率响应函数是指在复频率域上，将输入信号的频谱与输出信号的频谱之比来描述系统的特性。

离散系统的频率响应函数可以通过系统的传输函数来求得。

传输函数是指系统输出信号与输入信号的拉普拉斯变换之比。

对于离散系统，传输函数可以通过系统的差分方程求解。

然后，使用z变换将差分方程转化为传输函数的形式。

通过传输函数，我们可以得到离散系统的频率响应函数，从而分析系统在不同频率下的特性。

离散系统的频率响应函数通常使用幅频响应和相频响应来描述。

幅频响应表示系统在不同频率下的输出信号的幅度与输入信号的幅度之比，相频响应表示系统在不同频率下的输出信号与输入信号的相位差。

通过幅频响应和相频响应，可以分析系统在不同频率下的输出信号的放大倍数和相位延迟情况。

接下来，我们来介绍离散系统的零极点分布。

离散系统的零点是指系统传递函数的分子多项式所对应的根，零点表示系统在一些频率下对输入信号的抑制或增强。

离散系统的极点是指系统传递函数的分母多项式所对应的根，极点表示系统在一些频率下的共振或抑制。

离散系统的零点和极点在复平面上的分布情况对于系统的稳定性和频率响应特性有着直接的影响。

离散系统的零极点分布的分析方法通常可以使用极坐标图或者单位圆图来表示。

极坐标图将离散系统的零点和极点用复数的模和幅角表示，通过观察零点和极点的分布情况，可以初步判断系统的稳定性和频率响应特性。

更进一步地，可以使用单位圆图来表示离散系统的零点和极点在单位圆上的分布情况。

单位圆图可以直观地显示系统的极点与零点对于频率响应的影响，通过观察单位圆图可以得到离散系统的稳定性和频率响应特性的更详细的信息。

全通系统零极点分布特点
全通系统是指其传递函数为全纯函数的线性时不变系统，也就是说其极点都处于复平面内部。

零极点分布是指全通系统中的零点和极点分布在复平面上的位置。

以下是全通系统零极点分布的特点：
1. 极点均在复平面内部
全通系统的传递函数为全纯函数，因此其极点均在复平面内部。

这意味着全通系统的稳定性比其他系统更好。

2. 零点和极点通常成对出现
在全通系统中，零点和极点通常成对出现。

这是由于传递函数是分子多项式与分母多项式的比值所决定的。

如果分母多项式有一个零点，那么传递函数将有一个极点。

同样，如果分子多项式有一个零点，那么传递函数将有一个零点。

因此，在全通系统中，零点和极点的数量通常相等。

3. 零点和极点的位置对系统的性能有影响
在全通系统中，零点和极点的位置对系统的频率响应和稳定性有很大
的影响。

具体来说，零点决定了系统的增益和截止频率，而极点决定
了系统的稳定性和振荡频率。

因此，设计全通系统时需要注意这些因素，并选择合适的零点和极点位置。

4. 零点和极点的数量对系统的复杂度有影响
在全通系统中，零点和极点的数量决定了系统的复杂度。

具体来说，
零点和极点的数量越多，系统的复杂度就越高。

因此，在设计全通系
统时需要考虑性能和复杂度之间的平衡。

综上所述，全通系统的零极点分布对系统的性能和稳定性有重要影响。

在设计全通系统时，需要注意零点和极点的数量和位置，并选择合适
的参数以取得最佳的系统性能。

matlab ‎实验二 系统稳定性
一、演示内容：
例1、 已知传递函数‎2
724364523)(2345234+++++++++=s s s s s s s s s s G ，判断系统的稳‎定性。

方法一：在命令窗口，求出系统极点‎的值，判断系统的稳‎定性
注释：
num=[3,2,5,4,6]; 传递函数的分‎子按照降幂排‎列，系数按顺序存‎放。

den=[1,3,4,2,7,2];传递函数的分‎母按照降幂排‎列，系数按顺序存‎放。

sys=tf(num,den); 由上面的分子‎和分母构成传‎递函数
p=pole(sys); pole 是求‎这个传递函数‎的极点，然后保存在p ‎这个变量里面‎。

p 输入p 这个变‎量，然后回车，可以输出p 里‎面所存放的变‎量，如图一所
示。

图一
也可以双击w‎o rkspa‎c e里面的p‎和sys可分‎别观察p和s‎y s的值。

（这里存放了每‎个变量的值），如图二、图三所示。

p--→ sys--→
图二图三
方法二：求特征方程的‎根
roots是‎用来求方程的‎根，roots（[1,3,4,2,7,2]）括号内是特征‎方程的系数。

方法三：直接绘出系统‎的零极点图
首先，在命令窗口输‎入c lc可以‎清空屏幕。

pzmap（）是绘制零极点‎图的命令。

（）内是传递函数‎名称。

其中x表示极‎点，o表示零点。

方法四：将传递函数直‎接转换为零极‎点增益型
其中，z表示零点，p表示极点，k为增益。

二、实验内容(上交)
1用上述四种‎方法，完成书本P3‎2 2-5 。

ctle电路零极点分布CTLE电路是一种用于增强信号的电路，在数字通信中广泛应用。

CTLE电路具有零极点分布特性，这种特性对于电路的性能至关重要。

本文将就CTLE电路的零极点分布对电路性能的影响进行讨论。

首先，我们来了解一下CTLE电路的结构。

CTLE电路一般由一个放大器、一个低通滤波器和一个峰值探测器组成。

其中，放大器用于放大信号，低通滤波器用于滤除高频噪声，峰值探测器用于探测信号的峰值，以便进行自适应电平调整。

在CTLE电路中，零极点分布是一个重要的特性。

对于一般的放大器电路，它的传递函数可以表示为：H(s) = (a0 + a1s + ... + anx^n) / (1 + b1s + ... + bmx^m)其中，a0 ~ anx、b1 ~ bmx是常数。

我们可以将这个传递函数化简为一个分子项和一个分母项的乘积形式：H(s) = K * (s - z1) * (s - z2) * ... * (s - zn) / [(s - p1) * (s - p2) * ... * (s - pm)]其中，K是一个常数，zi是零点，pi是极点。

在这个式子中，分母项的极点决定了电路的增益和波形失真，如果它们处于高频区域，那么电路的增益会很低，波形失真也很明显。

分子项的零点决定了电路的频率和带宽，如果它们太远或太近，就会导致电路的频率响应不稳定。

其中，K是一个常数，zi是零点，pi是极点。

我们可以看到，CTLE电路的传递函数中有两个零点和两个极点。

这两个零点和极点的位置决定了CTLE电路的增益和带宽。

如果零点和极点的位置不合适，就会导致电路性能下降。

CTLE电路中的零点和极点的位置可以通过改变电路元件的参数来调整。

例如，可以改变放大器的增益、带宽和失调电压来改变传递函数中的零点和极点的位置。

一般来说，CTLE电路的零点应该在频率响应的斜率转折点上，而极点应该在零点附近，这样可以保证电路的频率响应稳定并且增益高。

现代控制系统课后习题答案现代控制系统课后习题答案现代控制系统是一门应用于工程领域的学科，它研究如何通过控制器来改变或维持系统的行为。

在学习这门课程时，我们常常会遇到一些习题，这些习题旨在帮助我们巩固所学的知识和技能。

在本文中，我将为大家提供一些现代控制系统课后习题的答案，希望能对大家有所帮助。

1. 什么是控制系统的稳定性？如何判断一个控制系统是否稳定？控制系统的稳定性是指系统在受到扰动或参数变化时，能够保持稳定的状态。

判断一个控制系统是否稳定的方法有很多，其中一种常用的方法是通过系统的传递函数进行判断。

如果系统的传递函数的所有极点都位于左半平面，则系统是稳定的；如果存在极点位于右半平面，则系统是不稳定的。

2. 什么是控制系统的零极点分布？如何分析一个控制系统的零极点分布？控制系统的零极点分布是指系统的传递函数中的零点和极点的位置。

零点是指传递函数为零的点，极点是指传递函数为无穷大的点。

分析一个控制系统的零极点分布可以通过对传递函数进行因式分解的方法来实现。

将传递函数分解为一系列一阶和二阶的因子，可以得到系统的零点和极点的位置。

3. 什么是控制系统的频率响应？如何绘制一个控制系统的频率响应曲线？控制系统的频率响应是指系统对不同频率的输入信号的响应情况。

绘制一个控制系统的频率响应曲线可以通过计算系统的传递函数在不同频率下的幅频特性和相频特性来实现。

幅频特性表示系统对不同频率的输入信号的幅值变化情况，相频特性表示系统对不同频率的输入信号的相位变化情况。

4. 什么是PID控制器？如何设计一个PID控制器？PID控制器是一种常用的控制器，它由比例项（P项）、积分项（I项）和微分项（D项）组成。

比例项用于根据误差的大小来调整控制器的输出，积分项用于根据误差的累积值来调整控制器的输出，微分项用于根据误差的变化率来调整控制器的输出。

设计一个PID控制器可以通过调整P、I和D三个参数来实现，通常需要根据系统的特性和需求来选择合适的参数值。