当前位置：文档之家 › 零极点分析ppt课件

零极点分析ppt课件

  • 格式：ppt
  • 大小：3.51 MB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

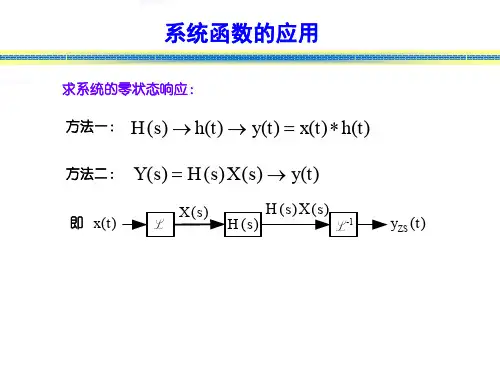
信号与系统系统函数的零极点分析课件

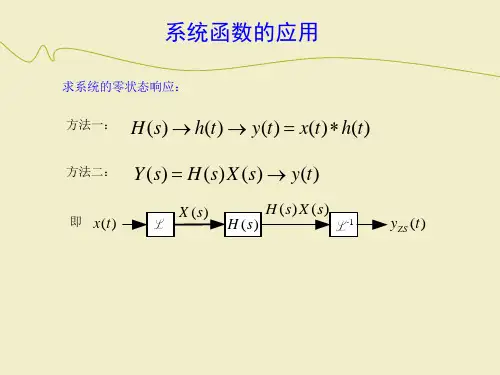
信号与系统系统函数的零极点分析课件
极点影响系统噪声性能
极点的位置也会影响系统的噪声性能，极点靠近虚轴时，系统对噪声的抑制能力较强。
极点对系统稳定性的影响
实数极点影响系统稳定性
实数极点会使得系统函数在某点趋于无穷大，导致系统不稳 定。极点的位置决定了系统稳定的程度和响应速度。
复数极点影响系统稳定性
复数极点会影响系统的频率响应特性，进而影响系统的稳定 性。如果复数极点位于左半平面，则系统稳定；反之，位于 右半平面则不稳定。
零点与系统极点的关系
在复平面内，零点和极点可以影响系统的稳定性，极点的位置更为 关键。
稳定系统中的零点作用
在稳定的系统中，零点可以起到调节系统性能的作用，但不会改变 系统的稳定性。
零点对系统频率响应的影响
零点对低频响应的影响
某些零点的位置会影响系统的低频响应，可能导致低频增益降低 或相位滞后。
零点对高频响应的影响
傅里叶分析
将信号分解为不同频率的正弦波 和余弦波，研究信号的频谱特性 和系统的频率响应。
拉普拉斯变换
将时域函数转换为复平面上的函 数，通过分析系统的传递函数来 研究系统的稳定性、极点和零点 等特性。
Z变换
将离散时间序列转换为复平面上 的函数，通过分析系统的差分方 程来研究离散时间系统的特性。
系统函数与零极点
频率响应分析
零极点分布影响系统的频率响应特性，通过分析零极点 可以预测系统的频率合理设计系统的零极点，可以实现特定的系统性能 指标，如快速响应、低超调量等。
系统函数的零点分析
03
零点对系统性能的影响
零点位置影响系统性能
01
零点位置的不同会导致系统性能的差异，例如系统的幅频特性
极点的定义与性质
定义
极点是系统函数在复平面上具有无穷大 增益的点，即系统函数的分母为零的点。

零极点分析(高等教学)

零极点分析(高等教学)

5.1.1 系统函数的定义
设系统的 n 阶微分方程为：
an y(n) (t) an1 y(n1) (t) a1 y(1) (t) a0 y(t) bm x(m) (t) bm1x(m1) (t) b1x(1) (t) b0 x(t) 若 y(k) (0 ) 0, x(k ) (0 ) 0
（1）
对式（1）两边取拉氏变换得：
Yzs
(s)
bmsm an s n
bm1sm1 an1sn1
b1s b0 X (s) a1s a0
古柏文书
2
H (s)
Yzs (s) X (s)
bm s m an s n
bm1sm1 an1sn1
b1s b0 a1s a0
--------- “系统函数”或“网络函数”
t
（2）
v2 (t) h(t) x(t)
h( )x(t )d
0
t Ke Ee (t )d u(t) 0
KE (et et )u(t) ( )
古柏文书
10
x(t) Eetu(t)
H (s) K
s
或：
V2 (s) H (s) X (s)
KE
(s )(s )
KE [ 1 1 ]
第5章 连续时间系统的s域分析
5.1 系统函数与冲激响应
5.2 零、极点分布与时域响应特性
5.3 零、极点分布与系统的频率响应特性的关系
5.4 典型系统的频响特性
5.5 全通系统与最小相位系统
5.6 模拟滤波器的基本概念与设计方法
5.7 系统模拟及信号流图
5.8 系统的稳定性
古柏文书
1
5.1 系统函数与冲激响应
1Ω

零点与极点的关系ppt课件

零点与极点的关系ppt课件

m!(z
z0 )
d m1
lim
z z0
dz m 1
(z z0 )m
f (z)
(m 1)!c1 , 移项得(5)式.
24
当m=1时，式(5)即为式(4).
规则III
设f (z) P(z) Q(z)
P(z), Q(z)在z0处解析,
P(z0 ) 0, Q(z0 ) 0, Q'(z0 ) 0
12
“”若z0是
1 的m级零点,则 f (z)
f
1 (z)
(z
z0
)m
(z)
(z) 在z0解析,且 (z0 ) 0
.
当z
z0时，f
(z)
(z
1 z0 )m

1
(z)
(z
1 z0 )m
(z)
(z)在 z0 解析,且 (z0 ) 0 .
z0是f (z)的m级极点.
13
例
求f
(z)
(1
( g(z) (z)P(z)在z0解析,
且g(z0 ) 0), 则z0为f (z)的 级极点,由规则
Re
s[
f
(z),
z0
]
lim ( z
zz0
z0
)
f
(z)
lim P(z) P(z0 ) zz0 Q(z) Q(z0 ) Q'(z0 ) z z0
Q'(z0 ) 0
得证！
26
例1
计算:
f (z)
1 (z z0 )m
g(z)
g(z)在z0解析,且g(z0 ) 0
1 f (z)
(z z0 )m
1 g(z)

信号、系统分析与控制 第9章 系统函数的零极点

信号、系统分析与控制 第9章 系统函数的零极点

2. 离散系统函数的零极点
M
离散系统函数的多项式形式为：
H (z)
B(z) A(z)
bj z j
j0
N
ai z i
b0 a0
b1z 1 ... bm z m a1z 1 ... an z n
（9.1.2）
将系统函数进行因式分解，可采用根的形式表示多项式，即 i0
M
H (z)
Y (z)
➢ 说明系统正弦稳态特性。
➢ 研究系统的稳定性。从系统函数的极点分布可以了解系统的固有频率，进而了解系统冲激响应的模式，也就 是说可以知道系统的冲激响应是指数型、衰减振荡型、等幅振荡型、还是几者的组合，从而可以了解系统的
响应特性及系统是否稳定。
1. 连续系统的零极点
系统函数一般以多项式形式出现，分子多项式和分母多项式都可以分解成线性因子的乘积，即连续系统函数：
➢ 可预测系统的时域特性。确定系统函数H(s)、H(z)。 ➢ 可以用函数 [r,p,k]=residuez（num,den）完成部分分式展开计算系统函数的留数、极点和增益； ➢ 可以用函数sos=zp2sos（z,p,k）完成将高阶系统分解为2阶系统的串联。
➢ 描述系统的频响特性。从系统的零、极点分布可以求得系统的频率响应特性，从而可以分析系统的正弦稳态 响应特性。 使用h=freqz(num,den,w)函数可求系统的频率响应。
2. 使用多项式的roots()函数分别求出多项式和的根，获得系统函数的极点、零点。
3. 用用zero(sys)和pole(sys)函数直接计算零极点，sys表示系统传递函数。用法如下：
z = zero(sys)：返回 LTI模型 sys的零点z 的列向量。
[z,gain] = zero(sys)：同时返回增益gain。

信号与系统系统函数的零极点分析

信号与系统系统函数的零极点分析
5.7.1 系统函数零极点定义
系统函数零点：使 H (s) 0的 s 值。
系统函数极点：使 H (s) 的 s 值。
对系统函数分子分母多项式进行因式分解得
H (s) K (s z1)(s z2 ) (s zm ) (s p1)(s p2 ) (s pn )
m
(s zj)
两系统函数仅是零点不同，它们对应的冲激响应仅是响应幅度和相位不同， 响应波形的模式均为衰减振荡模式
信号与5系.7统.3二系、系统统函零数极的极点点与、零系点与统系频统频率率响特性应的关的系关系
频率特性 频率特性指系统在正弦信号激励下稳态响应随信号频率的变化情况。 实际上就是系统的傅里叶变换
主要是指幅频特性和相频特性。
离虚轴越远，指数衰减或增长越快，所以称为衰减因子，
若 0，响应为衰减形式，若 0 ，响应为增长形式，
若 0 ，响应振幅为常数。
（2）极点的虚部 决定了振荡的快慢， 离实轴越远，
振荡越快，称为振荡频率。若 0 ，响应不振荡。
信号与系统
系统零极点与系统时域响应的关系
K
j 1 n
(s pk )
k 1
在复平面上，零点用“o”表示，
极点用“×”表示，标出系统的
零极点的位置，称为系统的
零极点图
z1, z2 , , zm 是系统零点
p1, p2 , , pn 是系统极点
j
0

信号与系统
5.7.2 系统零极点与冲激响应模式的关系
1、极点的影响
H(s) 1 , s
令
j zr Nre jr
j pk M k e jk
有
m
m

信号与系统第六章 系统函数与零极点分析PPT课件

信号与系统第六章 系统函数与零极点分析PPT课件

信号与线性系统
三、通过系统函数表达式作出系统模拟图
H s Y Fs s b 1 n a b n n 1 1 s s 1 1 a b 1 1 s s n n 1 1 a b 0 0 s s n n
令m=n并不失一般性！
YsHsFsNsD Fss
设一个中间变量
X
s
p2
j
p4 j0
Tel:22896276
返回
广东医学院生物医学工程教研室
信号与线性系统
三、零点、极点与频域特性的关系 如果系统函数在s平面右半面没有极点，那么，系统的频 率特性就可以由下式确定：
HjHssj
m
m
szi
jzi
HsH0
i1 n
HjH0
i1 n
spj
jpj
j1
j1
E-mail:lynwindsent@
L-1
httet tsin0ttet sin0tt
系统函数极点为 p 1 0
p2
p 3 j 0
p 4 j 0
返回
E-mail:lynwindsent@
Tel:22896276
广东医学院生物医学工程教研室
j
信号与线性系统
j
p1 0
j
p3 j0
E-mail:lynwindsent@
系统函数也是系统冲击响应的象函数：
Hs htestdt
0
E-mail:lynwindsent@
Tel:22896276
返回
广东医学院生物医学工程教研室
信号与线性系统
如果激励信号是指数信号est，则系统响应为：
yt h e st d e sth e s d H se st

系统函数零极点分布决时域特性课件

系统函数零极点分布决时域特性课件

总结词
零点位置影响系统瞬态响应的速度和幅 度，极点位置影响系统阻尼和振荡特性 。
VS
详细描述
零点位置影响系统输出的初始状态。如果 存在接近虚轴的零点，系统的输出会迅速 达到稳定值。极点位置影响系统的阻尼特 性和振荡频率，靠近虚轴的极点会导致系 统阻尼慢，振荡时间长。
零极点分布与系统稳态误差的关系
总结词
零点位置对系统稳态误差的影响
总结词
零点位置影响系统稳态误差，靠近虚轴的零点导致稳态误差 增大。
详细描述
系统函数的零点位置也会影响系统的稳态误差。如果零点靠 近虚轴，系统的稳态误差会增大。这是因为这些零点使得系 统的极点在复平面的右侧，导致系统的极点远离虚轴，从而 使得系统的稳态误差增大。
04
极点分布对时域特性的影响
极点位置远离虚轴
系统瞬态响应较慢，因为远离虚轴的 极点会导致系统具有较小的时间常数 ，从而减缓瞬态响应。
极点位置对系统稳态误差的影响
极点位置靠近虚轴
系统稳态误差较小，因为虚轴附近的极点会导致系统具有较大的增益，从而减 小稳态误差。
极点位置远离虚轴
系统稳态误差较大，因为远离虚轴的极点会导致系统具有较小的增益，从而增 大稳态误差。
零点位置对系统瞬态响应的影响
总结词
零点位置影响系统瞬态响应，靠近虚轴的零点导致瞬态响应速度变慢。
详细描述
系统函数的零点位置也会影响系统的瞬态响应特性。如果零点靠近虚轴，系统的瞬态响应速度 会变慢。这是因为这些零点使得系统的极点在复平面的右侧，导致系统的极点远离虚轴，从而 使得系统的动态响应速度变慢。
稳态误差
系统在输入信号的作用下，实际 输出与理想输出之间的偏差。
误差类型
包括静态误差和动态误差，静态误 差是指系统在稳态下的误差，动态 误差是指系统在过渡过程中产生的 误差。

零极点分析ppt课件

零极点分析ppt课件

Yzs (s)
bmsm bm1sm1 L b1s b0 ansn an1sn1 L a1s a0
X (s)
2
H (s)
Yzs (s) X (s)
bm s m an s n
bm1sm1 an1sn1
b1s b0 a1s a0
--------- “系统函数”或“网络函数”
简写为： H (s) Y (s) 或：Y (s) H (s) X (s) X (s)
i1 k 1
29
自由响应
强迫响应
例5-4：电路如图所示，输入信号x(t)=5cos2t u(t),求输出电压
y(t),并指出y(t)中的自由响应和强迫响应分量。
R=1Ω +
x(t)
C=1F
1
+ H (s) Y (s) sC 1
y(t)
X (s) R 1 s 1 sC
-
-
X
(s)
5s s2
1
s 1 s 2 s2 3s 2
例： 图示电路，开关S在t = 0时刻闭合，以v2(t)作为响应，
输入信号 x(t) Eetu(t),
S
x(t )
R1
C R2 v2 (t)
（1）求冲激响应h(t)；
(2）求输出电压v2(t)；
1
解:
（1） H (s) V2 (s) 1/ R2 sC K
流i(t),并指出i(t)中的自由响应与强迫响应、暂态响应与稳态响应各
分量。
LC
解：(1) 求激励信号x(t)的拉氏变换X(s)
x(t) i(t)
R
X (s)
Em 01
s2
2 01
(s

信号与系统 系统函数的零极点分析

信号与系统 系统函数的零极点分析

信号与5系.7统.3二、系系统统函零数极的极点点、与零系点与统系频统频率率特响性应的关的系关系
频率特性 频率特性指系统在正弦信号激励下稳态响应随信号频率的变化情况。 实际上就是系统的傅里叶变换
主要是指幅频特性和相频特性。
在系统是稳定的前提下，系统频率响应和系统函数的关系为
H (? ) ? H (s) 2)2
在虚轴上
h(t) ? t sin ωtu(t)，t ? ? ，h(t) 增幅振荡
信号与系统
5.7.2 系统零极点与冲激响应模式的关系
几种典型情况
j?
jω0
?α
O
? jω0
α
?
信号与系统
5.7.2 系统零极点与冲激响应模式的关系
总体来说，系统函数 H(极s) 点 p ?对? ?时j?域响应特性关系如下
5.7.1 系统函数零极点定义
系统函数零点：使 H (s) ? 0 的 s 值。
系统函数极点：使 H ( s ) ? ? 的 s 值。
对系统函数分子分母多项式进行因式分解得
H (s) ? K(s ? z1)(s ? z2 )L (s ? zm ) (s ? p1)(s ? p2 )L (s ? pn )
将矢量图画在复平面内
信号与系统
五．零极点与系统频率响应的关系
零点： j? ? zr ? Nr e j? r
Nr
zr
?r
jω
σ
O
极点: j? ? pk ? Mke j?k
?k
pk
zr
Mk
Nr
?r
jω
σ
O
信号与系统
五．零极点与系统频率响应的关系
H (? ) ? K
r ?1 n

信号与系统 系统函数的零极点分析

信号与系统 系统函数的零极点分析

M ke jk
k 1
k 1
将 j zr j 都p看k 作是两矢量之差，
将矢量图画在复平面内
五．零极点与系统频率响应的关系
零点： j zr Nre jr
Nr
zr
r
jωσ O极点: j Nhomakorabeapk M k e jk
k pk
zr
Mk
Nr r
jω
σ O
五．零极点与系统频率响应的关系
定性地画系统的幅频特性时 的规律：
五．零极点与系统频率响应的关系
(4) 虚轴若有零点 zr ，j则r 当 通过j零点
H () 0
(5) 虚轴若有极点 pk j，则k 当 通过j极点
H ()
zr 时，jr p时k ， jk
(6) 在 j 处主要看零点极点的个数，
若零点比极点多，则 H ()
若极点比零点多，则 H () 0
5.7.2 系统零极点与冲激响应模式的关系
1、极点的影响
H (s)
1 s2
极点在原点
h(t) tu(t),t , h(t)
重 极
H
(s)
(s
1 a)2
极点在实轴上
点 h(t) t et u(t)，α 0，t ，h(t) 0
H
(s)
2ωs (s2 ω2
)2
在虚轴上
h(t) t sin ωtu(t)，t ，h(t) 增幅振荡
h1(t) L1[H1(s)] et cos(3t)u(t)
h2 (t) L1[H2 (s)] et cos(3t)u(t) et sin(3t)u(t) et[cos(3t) sin(3t)]u(t) et 2 sin(3t 45o )u(t)

域分析_极点和零点PPT讲稿

域分析_极点和零点PPT讲稿
现在您浏览的位置是第十三页，共一百零一页。
（3） 有二重极点分布——
(b)在负实轴上有二重极点
j
h(t)
0
t
1
H (s) (S )2
h(t) tet
现在您浏览的位置是第十四页，共一百零一页。
（3） 有二重极点分布——
(c)在虚轴上有二重极点
j
h(t)
0
t
H (s)
2S (S 2 12 )2
B
1 1
e eT
现在您浏览的位置是第二十八页，共一百零一页。
§5.2 由系统函数决定系统频率 特性
• 什么是系统频率响应？
不同频率的正弦激励下系统的稳态响应一般 为复数，可表示为下列两种形式：
H ( j) R( j) jI ( j) H ( j ) H ( j ) e j( j)
现在您浏览的位置是第二十九页，共一百零一页。
（4） 零点的影响
H1(s)
(s
sa
a)2 2
H2 (s)
(s
s a)2
2
z0
零点移动 到原点
z0
h(t) eat cost
h(t) eat 1 a 2 cos(t )
tg 1( a )
现在您浏览的位置是第二十页，共一百零一页。
（4） 零点的影响
• 零点的分布只影响时域函数的幅度和相
i1
ki s pi
n
n
kie pit
hi (t)
i 1
i 1
总特性
第 i个极点决定
现在您浏览的位置是第四页，共一百零一页。
（2） 几种典型的极点分布—— (a)一阶极点在原点
j
h(பைடு நூலகம்)

信号与系统系统函数的零极点分析

信号与系统系统函数的零极点分析
信号与系统
系统函数的应用
求系统的零状态响应： 方法一： 方法二：
H (s) h(t ) y(t ) x(t ) h(t ) Y (s) H (s) X (s) y(t )
L
即 x (t )
X (s)
H (s)
H (s) X (s)
L -1
yZS (t )
信号与系统
§5.7系统函数的零极点分析
( j zr ) ( j pk )
k 1 r 1 n
m
K
j r N e r jk M e k k 1 r 1 n
m
将
j zr j pk
都看作是两矢量之差，
将矢量图画在复平面内
信号与系统
五．零极点与系统频率响应的关系
j zr N r e jr
在系统是稳定的前提下，系统频率响应和系统函数的关系为
H ( ) H ( s ) s j
用零极点形式表示为
H ( ) H ( s ) s j K
( j z ) ( j p
k 1 r 1 n r k
m
)
信号与系统
则系统的幅频特性为 H ( ) K

0

信号与系统
五．零极点与系统频率响应的关系
j
H ( )
0
j

0
H ( )

0

0

信号与系统
五．零极点与系统频率响应的关系
j
H ( )
0

0

j
H ( )
0

0

信号与系统
【例 5-7-3】非常详细，自学。

自动控制 根轨迹(极点,零点)ppt课件

自动控制 根轨迹(极点,零点)ppt课件
自动控制 根轨 迹(极点,零点)
控制系统的稳定性，由其闭环极点唯一确定，系统暂态 响应和稳态响应的基本特性与系统的闭环零、极点在S平面 上分布的位置有关。 决定系统基本特性的是系统特征方程的根，如果搞清楚 这些根在S平面上的分布与系统参数之间的关系，那就掌握 了系统的基本特性。 为此目的，依万斯（W.R.EVans）在1984年提出了根轨 迹法，令开环函数的一个参数——开环增益Ｋ（或另一个感 兴趣的参数）从0变化到∞，与此对应，特征方程的根，便在 S平面上描出一条轨迹，称这条轨迹为根轨迹。
× p3
§4-2 绘制根轨迹的基本规则
绘制根轨迹的基本规则实际上是系统根轨迹的一些基本 性质，掌握了这些基本规则，将能帮助我们更准确、更迅速 的绘制根轨迹。
一．根轨迹的对称性
实际系统的特征方程的系数是实数，其特征根为实数 或共轭复数，因此，根轨迹对称于实轴。
二．根轨迹的起点和终点
根轨迹的起点对应于 K 1 0 时特征根在S平面上的分布 时，特征根在S平面 位置，而根轨迹的终点则对应于 K 1 上的分布位置。
j i 1 i
（＊＊）
§４－１根轨迹的基本概念
三．根据相角条件确定根轨迹上的点
设某一系统的开环零极点如图，在Ｓ 平面中的任意一点 S0 ，用相角条件可
s0
O
× p2
以判断 S0 是不是根轨迹的点。
1、从 S0 到各零极点连直线
(s ) 2、用量角器量 ，…等各个角 0 p 1
O z1
×p 1
jω
∞ K K=0
（1）当0<K< 0.25时，闭环特征根为
实根，系统是过阻尼状态，阶跃响应为
非周期过程。 （2）当K＝0.25时，两特征根重合， 均为-0.5，系统处于临界阻尼状态。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
零，求电流i(t)。
x(t)
x(t) Vm sin(t)
X
(s)
Vm s2
2
H
(s)
I (s) X (s)
1 sL
R
1 L
s
1 R
L
--------- 策动点导纳函数
5
I(s) H (s)X (s) 1 1 Vm L s R s2 2
L
i(t)
Vm 2 L2
R2
Rt
Le L
R 2 2 L2
arctan L
sin(t
)
R
+
H (s) VR (s) R X (s) R sL
x(t)
vR(t)
R 1
L sR
-
L
--------- 转移电压比（电压传输函数6 ）
5.1.2 系统函数H(s)与冲激响应h(t)的关系
Yzs (s) H (s) X (s)
当 x(t) (t) 时， yzs (t) h(t) 而 X (s) [ (t)] 1
3
dy (t ) dt
2 y(t)
x(t )
求H(s)。
解法一：对微分方程两边取拉氏变换得：
(s2 3s 2)Y (s) X (s)
Y (s)
1
H (s) X (s) (s2 3s 2)
8
解法二：先求系统的冲激响应（应用2.3节的方法）
h(t) (et e2t )u(t)
则 H (s) 1 1
Yzs (s) H (s)
所以
h(t) 1[H (s)]
或
H (s) [h(t)]
简记为： h(t)
H (s)
7
5.1.3 系统函数H(s)的求法
（1）由零状态下系统的微分方程经拉氏变换求得
（2）由冲激响应的拉氏变换求得
（3）用零状态下的s域模型、应用电路分析方法求得
例5-1：已知
d
2 y(t) dt 2
H
(s)
Y21
(s)
I2 V1
(s) (s)
1Ω
1F I3(s) 1F
+
V1(s) -
I1(s)
1Ω I2(s)
1Ω
12
1Ω
1F I3(s) 1F
+
V1(s) -
I1(s)
1Ω I2(s)
1Ω
解：列写回路方程
(1 s
1)
I1
(s)
I2
(s)
1 s
I3
(s)
V1
(s)
I1
(s)
(1 s
2)I
2
(s)
5.1.1 系统函数的定义
设系统的 n 阶微分方程为：
an y(n) (t) an1 y(n1) (t) a1 y(1) (t) a0 y(t) bm x(m) (t) bm1x(m1) (t) b1x(1) (t) b0 x(t) 若 y(k) (0 ) 0, x(k ) (0 ) 0
14
I 2 (s)
2
s2 2s 1 s2 5s 2 V1(s)
Y21(s)
I2 (s) V1(s)
s2 s2
2s 1 5s 2
15
5.2 零、极点分布与时域响应特性
f (t)
F(s)
h(t)
H (s)
H(s)能否反映h(t)的特性？
5.2.1 零点与极点的概念
H
(s)
bm s m an s n
KE (et et )u(t) ( )
10
x(t) Eetu(t)
H (s) K
s
或：
V2 (s) H (s) X (s)
KE
(s )(s )
KE [ 1 1 ]
s s
v2 (t)
KE
(et
et )u(t)
( )
11
例5-2：求下图电路的转移导纳函数
1
s 1 s 2 s2 3s 2
例： 图示电路，开关S在t = 0时刻闭合，以v2(t)作为响应，
输入信号 x(t) Eetu(t),
S
x(t )
R1
C R2 v2 (t)
（1）求冲激响应h(t)；
(2）求输出电压v2(t)；
1
解:
（1） H (s) V2 (s) 1/ R2 sC K
1 s
I3
(s)
0
1 s
I1
(s)
1 s
I
2
(s)
(
2 s
1)I3
(s)
0
13
1 1 s 1 1
s
1
12 s
1 s
1
s
1 s
s2
5s s2
2
2 1
s
1 1 s
V1(s)
2 1
0
1 0 s
1s1 s源自s22s s21 V1(s)
2 1
s
I2(s)
2
s2 2s 1 s2 5s 2 V1(s)
第5章 连续时间系统的s域分析
5.1 系统函数与冲激响应 5.2 零、极点分布与时域响应特性 5.3 零、极点分布与系统的频率响应特性的关系 5.4 典型系统的频响特性 5.5 全通系统与最小相位系统 5.6 模拟滤波器的基本概念与设计方法 5.7 系统模拟及信号流图 5.8 系统的稳定性
1
5.1 系统函数与冲激响应
简写为： H (s) Y (s) 或：Y (s) H (s) X (s) X (s)
X(s)
H(s)
Y(s)
注意：1、H(s)独立于输入，仅由系统特性决定；
2、系统函数是在零状态条件下得到的； 3、线性时不变系统的H(s)是s的有理函数。
3
H(s)名称的含义
4
例：下示电路在t=0时开关S闭合，接入信号源x(t),电感起始电流为
X (s)
R1
1
/
1 R2
sC
s
9
K
x(t )
R1
C R2 v2 (t)
x(t) Eetu(t)
H (s) K
s
其中：
K 1 , R1 R2
R1C
R1R2C
h(t) 1[H (s)] Ke tu(t)
t
（2）
v2 (t) h(t) x(t)
h( )x(t )d
0
t Ke Ee (t )d u(t) 0
（1）
对式（1）两边取拉氏变换得：
Yzs (s)
bmsm bm1sm1 L b1s b0 ansn an1sn1 L a1s a0
X (s)
2
H (s)
Yzs (s) X (s)
bm s m an s n
bm1sm1 an1sn1
b1s b0 a1s a0
--------- “系统函数”或“网络函数”
p1 p2 1
极点：
p3
2
j
j
p4
2
j
s1 0
-j
零点：
s2 s3
1 1
j j
s4
只要知道H(s)在s平面中零极点分布
h(t)波形的特性
17
H(s)在s平面中零极点分布特点： 1. 若系统为实系统，则H(s)的零极点为复数零极点必然成
bm1sm1 L
an
sn1
1
L
b1s b 0 B(s) a1s a 0 A(s)
若
lim
s pi
H
(s)
, 则pi为极点；
若
lim
s zi
H
(s)
0，则zi为零点。
16
s[(s 1)2 1] s(s 1 j)(s 1 j) H (s) (s 1)2(s2 4) (s 1)2(s 2 j)(s 2 j)