2 叶片式流体机械中的能量转换

第⼀章流体机械的定义及分类习题第⼀章流体机械的定义及分类习题1、流体具有的能量主要包括哪⼏个⽅⾯？2、什么是流体机械？根据什么将流体机械分为叶⽚式流体机械和容积式流体机械？3、什么是往复式流体机械和回转式流体机械？试分别列举⼏种型式。

第⼆章叶⽚式流体机械概述习题1、⽔轮机和⽔泵的基本⼯作参数有哪些？各是如何定义的？2、什么是流体机械？根据什么将流体机械分为叶⽚式流体机械和容积式流体机械？3、什么是往复式流体机械和回转式流体机械？试分别列举⼏种型式。

4、往复式泵的⼯作原理是什么？5、齿轮泵的⼯作过程是什么？齿轮泵的容积效率怎样计算？6、反击型⽔轮机的主要过流部件名称及作⽤是什么？试以混流式为例绘出其单线图。

7、根据⽔轮机利⽤⽔流能量⽅式的不同将⽔轮机分为哪两⼤类？⼜根据转轮区域⽔流流动⽅向特征的不同将反击式⽔轮机分为了⼏种？试分别说出各⾃的特点和使⽤范围。

8、反击式⽔轮机由哪四⼤部件组成？试分别说出它们的作⽤。

9、试说明液⼒变矩器的组成和⼯作原理。

10、什么是⽓压传动？以剪切机为例，说明⽓压传动的⼯作原理。

11、试推导往复泵吸⽔、压⽔过程中活塞上压强的表达式。

12、试证明：单作⽤往复泵安装空⽓室活塞克服管路摩擦所作的功，与不装空⽓室活塞克服管路摩擦所作的功之⽐为。

假定摩擦系数不随速度变化。

第三章叶⽚式流体机械中的能量转化习题1、总扬程为25m，流量为3m3/min，泄漏量为流量的3%的离⼼泵以1450rpm的转速运转时，泵的轴功率为14.76kw，机械效率取，试求下列值：（1）泵的有效功率；（2）泵的效率；（3）容积效率；（4）⽔⼒效率。

2、⽔轮机效率实验时在某⼀导叶开度下测得下列数据：蜗壳进⼝处压⼒表读数P=22.6×104p a，压⼒表中⼼⾼程Hm=88.5m，压⼒表所在钢管直径D=3.35m，电站下游⽔位?=85m，流量q v=33m3/s，发电机功率P g =7410Kw，发电机效率ηg=0.966，试求机组效率及⽔轮机效率。

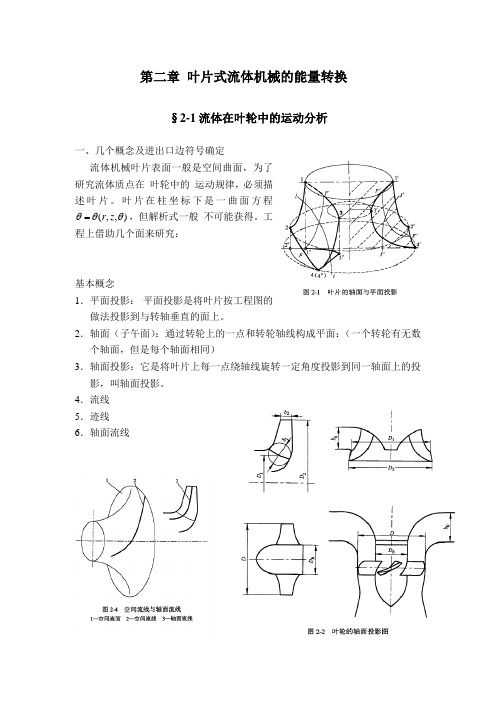
第二章 叶片式流体机械的能量转换§2-1流体在叶轮中的运动分析一、几个概念及进出口边符号确定流体机械叶片表面一般是空间曲面，为了研究流体质点在 叶轮中的 运动规律，必须描述叶片。

叶片在柱坐标下是一曲面方程),,(θθθz r =，但解析式一般 不可能获得。

工程上借助几个面来研究： 基本概念1．平面投影： 平面投影是将叶片按工程图的做法投影到与转轴垂直的面上。

2．轴面（子午面）：通过转轮上的一点和转轮轴线构成平面：（一个转轮有无数个轴面，但是每个轴面相同）3．轴面投影：它是将叶片上每一点绕轴线旋转一定角度投影到同一轴面上的投影，叫轴面投影。

4．流线5．迹线 6．轴面流线进出边符号确定：（本书规定） P 代表高压边 P 对风机，泵，压缩机，一般S 代表低压边 出口边对水轮机进口边S 对风机，泵，压缩机，一般是进口边，对水轮机是出口边二、叶轮中的介质运动 1．速度的合成与分解：流体机械的叶片表面是空间曲面，而转轮又是绕定轴旋转的，故通常用圆柱坐标系来描述叶片形式及流体介质在转轮中的运动。

在柱坐标中，空间速度矢量式可分解为圆周，径向，轴向三个分量。

u z r C C C C++= 将C z ,C r 合成得C m , z r m C C C+= C m 位于轴面内（和圆周方向垂直的面），故又叫轴面速度。

2．绝对运动和相对运动：在流体机械的叶轮中，叶片旋转，而流体质点又有相对转轮的运动，这样根据理论力学知识质：叶轮的旋转是牵连运动。

流体质点相对于叶轮的运动叫相对运动，其速度叫相对速度，这样，流体质点的绝对速度为 这两速度的合成，即 u w C += 其中 u是叶轮内所研究的流体质点的牵连速度在流体机械的静止部件内，没有牵连速度，相对运动的轨迹和绝对运动重合。

用速度三角形，表示上述关系，即得：依速度合成分解，将C 分解为沿圆周方向的分量C u 及轴面上的分量C m ，从速度三角形知：C m =W m u u W C u +=或u u W C u-=叶轮内，每一点都可作出上述速度三角形。

§1-2 叶片式流体机械的主要性能参数一、流量1、定义：单位时间内流过一既定过流断面的流体的量2、常用符号Q ——体积流量（v q ） Av Q =G ——重量流量（G q ） 在风机的设计中常用Q G γ=→g ργ=3、单位Q ：m 3/h ，m 3/s ，L/s G:N/h* 对于水轮机：进口断面 对于泵轮机：出口断面二、能量头：机械进出口断面单位重量、体积介质的能量差值 （一）水轮机的工作水头1、定义：单位重量水从水轮机的进口至出口所减少的能量2、常用符号：H3、单位：米（水柱）mH 2Oo i E E H -=gcg p Z E h gc g p Z g c g p Z E oo o o o iA AA A A i i i i i 222222αραραρ++=∆-++=++=-如果取距水轮机有一定距离的下游断面T-T 断面为出口断面i A A i h Z E -∆-≈T o Z E ≈取下游水面为基准面 i A st h H H -∆-=（二）泵的扬程1、定义：单位重量液体从泵进口至泵出口所增加的能量2、常用符号：H3、单位：米（液柱）4、公式i o E E H -=gv g p Z E gv g p Z E ii i i i o o o 22220αραρ++=++=M g pg p a o +=ρρ V gpg p a i -=ρρ gc c V M h H i i o o 210006.139800108.9224αα-++⨯+= （三）风机的全压1、定义：单位体积的气体从风机的进口断面到风机的出口断面所获得的全压增值即：全压=静压+动压d st p p p +=st p ——与流动方向平行的表面压力 d p ——由动能转换而来的压力2、单位：N/m 23、表达式)()(1122.d st d st p p p p p +-+=规定：gc p pd d 22222αγ==则 )2(21112gc p p p st st st αγ+-=三、转速1、定义：主轴每分钟的转数2、单位：rpm ，r/min3、常用符号：n4、说明：n 变则性能改变 四、功率与效率（一）水轮机的功率和效率 1、水轮机的轮入功率 QH γQ 有一部分q 损失了，通过水轮机做功的实际流量q q Q Q QqQ q Q ηξ=-=-=-)1()1( Qqq =ξ——相对容积损失，q η——容积效率 水流真正付给转轮的功率H Q q ηγ，但一部克服水力损失，h h ∆h q h h Q P ∆=∆ηγHhH Q P h q h h ∆=∆=ηγξ相对流动损失h h ηξ=-1——流动效率运转的过程克旋转阻力，圆盘损失d P ∆hq dd H Q P ηηγξ∆=相对盘旋损失，d d ηξ=-1——内部机械效外部机械摩擦损失，m N ∆（轴同V ）HQ P q mM ηγξ∆=相对外部机械摩擦损失M η外部机械效率 水轮机的输出功率ηγηηηηγξξξηγξξξηγηγ⋅=⋅⋅⋅=---≈---=∆-∆-∆-=QH QH H Q H Q N N N H Q N m d h q m d n q m d h q Md h q )1)(1)(1()1( m d h q ηηηηη⋅⋅⋅=（二）泵与风机的功率和效率 1、输入功率 N ——轴功率 2、机械损失轴承轴封 2232D u 圆盘摩擦NN N mm ∆-=η3、容积损失和容积效率v N ∆qQ Q H q Q QH P P P P P qH T T m v m q T +=+=∆-∆-∆-=)(γγηγ4、流动损失和流动效率h P ∆TT q M e h H HQH QH P P P P ==∆-∆-=γγη T ——∞T5、有效功率 QH γ，QP6、总效率m q h ηηηη⋅⋅=h q M h h h h h H gQ gQH h H q Q g h H gQ P h H q Q g P P ηηηρρρρρη⋅⋅=∆+∆++∆+∆++==)())(()())((入入出水轮机⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧∆-=-=、输出功率（轴功率）、流动损失：、容积损失：内部机械损失圆盘损失轴封磨擦损失轴承磨擦损失 、机械损失、输入功率：54321H h H Q q Q or gQH h hqηηρ 泵⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧=∆+==+=（风机）；泵）：、输出功率（有效功率、流动损失：、容积损失：内部机械损失圆盘损失轴封磨擦损失轴承磨擦损失 、机械损失、输入功率（轴功率）Qp gQH H H h H H Q Q q Q Q or T h h T q )(54321ρηη例题：离心泵装置如图向某压力水箱供水，已知箱中液面压力2.196=''p kPa （表压），进出水管管路水力损失m 3=w h ，试求：（1） 泵在该系统中运行，泵扬程H 是多少米？（进水箱开敞，液面压力为大气压，进出水箱液面高差为2米。