第32讲 平面几何选讲

高中数学教案平面解析几何高中数学教案：平面解析几何引言：平面解析几何是高中数学重要的内容之一。

通过研究二维平面上的点、直线、圆、曲线等几何图形，我们可以建立起几何与代数的联系。

本文将介绍平面解析几何的基本概念、性质和解题方法，帮助学生深入理解和掌握该知识点。

一、直线的方程直线是平面解析几何中最基本的图形之一。

我们通常用方程来表示一条直线。

比如，对于一条过点A(x₁, y₁)和B(x₂, y₂)的直线L，其方程可表示为(y-y₁)/(y₂-y₁) = (x-x₁)/(x₂-x₁)。

通过这个方程，我们可以计算直线上的任意点的坐标。

二、直线的性质1. 平行和垂直关系：两条直线平行的条件是它们的斜率相等，而两条直线垂直的条件是它们的斜率的乘积为-1。

2. 直线的距离和点到直线的距离：通过点到直线的距离公式，我们可以计算直线与点之间的距离，从而解决相关问题。

3. 直线的判定：通过方程的形式以及两点确定直线的方法，可以判定给定的点是否在直线上。

三、圆的方程与性质圆是平面解析几何中另一个重要的图形。

我们通过圆心坐标和半径来表示一个圆。

对于圆心坐标为(h, k)、半径为r的圆，其方程可表示为(x-h)² + (y-k)² = r²。

1. 切线和法线：给定一条圆的方程和一点在圆上，我们可以求出与该圆相切或垂直的直线方程，通过圆的性质进行计算。

2. 圆与直线的位置关系：通过圆的方程和直线的方程，我们可以判断它们的位置关系，包括相离、相切和相交等情况。

四、曲线的方程与性质曲线是平面解析几何的高级内容，包括抛物线、椭圆、双曲线等。

每种曲线都有其特定的方程和性质。

1. 抛物线的方程与性质：抛物线可由一元二次方程表示，其顶点坐标和对称轴方程可以通过方程的形式直接读取。

2. 椭圆与双曲线的方程与性质：通过方程的参数与常数，我们可以得到椭圆和双曲线的离心率、焦点坐标等关键信息。

五、解析几何的应用平面解析几何有广泛的应用，例如在工程、物理、经济学等领域。

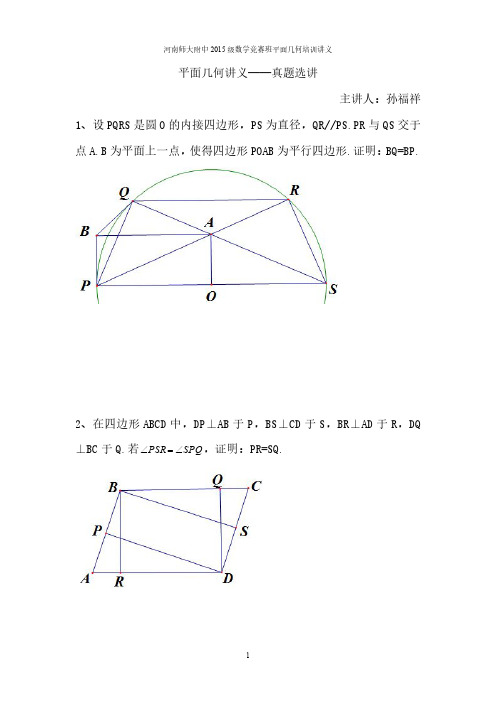
第一讲注意添加平行线证题在同一平面内,不相交的两条直线叫平行线.平行线是初中平面几何最基本的,也是非常重要的图形.在证明某些平面几何问题时,若能依据证题的需要,添加恰当的平行线,则能使证明顺畅、简洁.添加平行线证题,一般有如下四种情况.1、为了改变角的位置大家知道,两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.利用这些性质,常可通过添加平行线,将某些角的位置改变,以满足求解的需要.例1、设P、Q为线段BC上两点,且BP＝CQ,A为BC外一动点(如图1).当点A运动到使∠BAP＝∠CAQ时,△ABC是什么三角形？试证明你的结论.答：当点A运动到使∠BAP＝∠CAQ时,△ABC为等腰三角形.证明：如图1,分别过点P、B作AC、AQ的平行线得交点D.连结DA.在△DBP＝∠AQC中,显然∠DBP＝∠AQC,∠DPB＝∠C.由BP＝CQ,可知△DBP≌△AQC.有DP＝AC,∠BDP ＝∠QAC.ADB P Q C图1于是,DA∥BP,∠BAP＝∠BDP.则A 、D 、B 、P 四点共圆,且四边形ADBP 为等腰梯形.故AB ＝DP.所以AB ＝AC.这里,通过作平行线,将∠QAC“平推”到∠BDP 的位置.由于A 、D 、B 、P 四点共圆,使证明很顺畅.例2、如图2,四边形ABCD 为平行四边形,∠BAF＝∠BCE.求证：∠EBA＝∠ADE.证明：如图2,分别过点A 、B 作ED 、EC 的平行线,得交点P,连PE. 由ABCD,易知△PBA≌△ECD.有PA ＝ED,PB ＝EC. 显然,四边形PBCE 、PADE 均为平行四边形.有∠BCE＝∠BPE,∠APE＝∠ADE.由∠BAF＝∠BCE,可知∠BAF＝∠BPE.有P 、B 、A 、E 四点共圆.于是,∠EBA ＝∠APE.所以,∠EBA＝∠ADE.这里,通过添加平行线,使已知与未知中的四个角通过P 、B 、A 、E 四点共圆,紧密联系起来.∠APE 成为∠EBA 与∠ADE 相等的媒介,证法很巧妙.2、欲“送”线段到当处利用“平行线间距离相等”、“夹在平行线间的平行线段相等”这两条,常可通过添加平行线,将某些线段“送”到恰当位置,以证题.例3、在△ABC 中,BD 、CE 为角平分线,P 为ED 上任意一点.过P 分别作AC 、AB 、BC 的垂线,M 、N 、Q 为垂足.求证：PM ＋PN ＝PQ.证明：如图3,过点P 作AB 的平行线交BD 于F,过点F 作BC 的平行线分别交PQ 、AC 于K 、G,连PG. ∥＝P E D G A B F C 图2A N E B Q K G CD M F P 图3由BD 平行∠ABC,可知点F 到AB 、BC两边距离相等.有KQ ＝PN. 显然,PD EP ＝FD EF ＝GD CG ,可知PG∥EC.由CE 平分∠BCA,知GP 平分∠FGA.有PK ＝PM.于是,PM ＋PN ＝PK ＋KQ ＝PQ.这里,通过添加平行线,将PQ“掐开”成两段,证得PM ＝PK,就有PM ＋PN ＝PQ.证法非常简捷.3 、为了线段比的转化由于“平行于三角形一边的直线截其它两边,所得对应线段成比例”,在一些问题中,可以通过添加平行线,实现某些线段比的良性转化.这在平面几何证题中是会经常遇到的.例4设M1、M2是△ABC 的BC 边上的点,且BM1＝CM2.任作一直线分别交AB 、AC 、AM1、AM2于P 、Q 、N1、N2.试证：AP AB ＋AQ AC ＝11AN AM ＋22AN AM . 证明：如图4,若PQ∥BC,易证结论成立. 若PQ 与BC 不平行,设PQ 交直线BC 于D.过点A 作PQ 的平行线交直线BC 于E.由BM1＝CM2,可知BE ＋CE ＝M1E ＋M2E,易知 AP AB ＝DE BE ,AQ AC ＝DE CE ,11AN AM ＝DE E M 1,22AN AM ＝DEE M 2. 则APAB ＋AQ AC ＝DE CE BE +＝DE E M E M 21+＝11AN AM ＋22AN AM . 所以,AP AB ＋AQ AC ＝11AN AM ＋22AN AM . 这里,仅仅添加了一条平行线,将求证式中的四个线段比“通分”,使公分母为DE,于是问题迎刃而解.A P E M 2M 1B Q N 1N 2图4例5、AD 是△ABC 的高线,K 为AD 上一点,BK 交AC 于E,CK 交AB 于F.求证：∠FDA＝∠EDA.证明：如图5,过点A 作BC 的平行线,分别交直线DE 、DF 、BE 、CF 于Q 、P 、N 、M.显然,AN BD ＝KA KD ＝AMDC .有BD·AM＝DC·AN. (1) 由BD AP ＝FB AF ＝BCAM ,有AP ＝BC AM BD ·. (2) 由DC AQ ＝EC AE ＝BC AN ,有AQ ＝BC AN DC ·. (3)对比(1)、(2)、(3)有AP ＝AQ.显然AD 为PQ 的中垂线,故AD 平分∠PDQ.所以,∠FDA＝∠EDA.这里,原题并未涉及线段比,添加BC 的平行线,就有大量的比例式产生,恰当地运用这些比例式,就使AP 与AQ 的相等关系显现出来.4、为了线段相等的传递当题目给出或求证某点为线段中点时,应注意到平行线等分线段定理,用平行线将线段相等的关系传递开去.例6在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN＝90°.如果BM2＋CN2＝DM2＋DN2,求证：AD2＝41(AB2＋AC2). 证明：如图6,过点B 作AC 的平行线交ND 延长线于E.连ME.由BD ＝DC,可知ED ＝DN.有△BED≌△CND. 于是,BE ＝NC.显然,MD 为EN 的中垂线.有 EM ＝MN. 图5M P A Q N F B D C E K 图6A N CD E B M由BM2＋BE2＝BM2＋NC2＝MD2＋DN2＝MN2＝EM2,可知△BEM 为直角三角形,∠MBE＝90°.有∠ABC＋∠ACB＝∠ABC＋∠EBC＝90°.于是,∠BAC ＝90°.所以,AD2＝221⎪⎭⎫ ⎝⎛BC ＝41(AB2＋AC2). 这里,添加AC 的平行线,将BC 的以D 为中点的性质传递给EN,使解题找到出路.例7、如图7,AB 为半圆直径,D 为AB 上一点,分别在半圆上取点E 、F,使EA ＝DA,FB ＝DB.过D 作AB 的垂线,交半圆于C.求证：CD 平分EF.证明：如图7,分别过点E 、F 作AB 的垂线,G 、H 为垂足,连FA 、EB.易知DB2＝FB2＝AB·HB,AD2＝AE2＝AG·AB.二式相减,得DB2－AD2＝AB·(HB－AG),或 (DB －AD)·AB＝AB·(HB－AG).于是,DB －AD ＝HB －AG,或DB －HB ＝AD －AG. 就是DH ＝GD.显然,EG∥CD∥FH.故CD 平分EF. 这里,为证明CD 平分EF,想到可先证CD 平分GH.为此添加CD 的两条平行线EG 、FH,从而得到G 、H 两点.证明很精彩.经过一点的若干直线称为一组直线束.一组直线束在一条直线上截得的线段相等,在该直线的平行直线上截得的线段也相等.如图8,三直线AB 、AN 、AC 构成一组直线束,DE 是与BC 平行的直线.于是,有BN DM ＝AN AM ＝NC ME ,即BN DM ＝NC ME 或ME DM ＝NCBN . 此式表明,DM ＝ME 的充要条件是BN ＝NC.A G D O HB FC E 图7图8AD B NC E M利用平行线的这一性质,解决某些线段相等的问题会很漂亮.例8如图9,ABCD 为四边形,两组对边延长后得交点E 、F,对角线BD∥EF,AC 的延长线交EF 于G.求证：EG ＝GF.证明：如图9,过C 作EF 的平行线分别交AE 、AF 于M 、N.由BD∥EF, 可知MN∥BD.易知 S△BEF＝S△DEF.有S△BEC＝S△ⅡKG－ *5ⅡDFC.可得MC ＝CN.所以,EG ＝GF.例9如图10,⊙O 是△ABC 的边BC 外的旁切圆,D 、E 、F 分别为⊙O 与BC 、CA 、AB的切点.若OD 与EF 相交于K,求证：AK 平分BC.证明：如图10,过点K 作BC 的行平线分别交直线AB 、AC 于Q 、P 两点,连OP 、OQ 、OE 、OF.由OD⊥BC,可知OK⊥PQ. 由OF⊥AB,可知O 、K 、F 、Q 四点共圆,有∠FOQ＝∠FKQ.由OE⊥AC,可知O 、K 、P 、E 四点共圆.有∠EOP＝∠EKP.显然,∠FKQ＝∠EKP,可知∠FOQ＝∠EOP.由OF ＝OE,可知Rt△OFQ≌Rt△OEP.则OQ ＝OP.于是,OK 为PQ 的中垂线,故 QK ＝KP.所以,AK 平分BC.综上,我们介绍了平行线在平面几何问题中的应用.同学们在实践中应注意适时添加平行线,让平行线在平面几何证题中发挥应有的作用. 图9A B M E F N D C GO 图10练习题1. 四边形ABCD 中,AB ＝CD,M 、N 分别为AD 、BC 的中点,延长BA 交直线NM 于E,延长CD 交直线NM 于F.求证：∠BEN＝∠CFN.(提示：设P 为AC 的中点,易证PM ＝PN.)2. 设P 为△ABC 边BC 上一点,且PC ＝2PB.已知∠ABC＝45°,∠APC＝60°.求∠ACB.(提示：过点C 作PA 的平行线交BA 延长线于点D.易证△ACD∽△PBA.答：75°)3. 六边形ABCDEF 的各角相等,FA ＝AB ＝BC,∠EBD ＝60°,S△EBD＝60cm2.求六边形ABCDEF 的面积. (提示：设EF 、DC 分别交直线AB 于P 、Q,过点E 作DC 的平行线交AB 于点M.所求面积与EMQD 面积相等.答：120cm2)4. AD 为Rt△ABC 的斜边BC 上的高,P 是AD 的中点,连BP 并延长交AC 于E.已知AC:AB ＝k.求AE:EC. (提示：过点A 作BC 的平行线交BE 延长线于点F.设BC ＝1,有AD ＝k,DC ＝k2.答：211k) 5. AB 为半圆直径,C 为半圆上一点,CD⊥AB 于D,E 为DB 上一点,过D 作CE 的垂线交CB 于F.求证：DE AD ＝FB CF .(提示：过点F 作AB 的平行线交CE 于点H.H 为△CDF 的垂心.)6. 在△ABC 中,∠A:∠B:∠C＝4:2:1,∠A、∠B、∠C 的对边分别为a 、b 、c.求证：a 1＋b 1＝c1.(提示：在BC 上取一点D,使AD ＝AB.分别过点B 、C 作AD 的平行线交直线CA 、BA 于点E 、F.)7. △ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.求证：FH＝HG.(提示：过点A作BC的平行线分别交直线DE、DF 于点M、N.)8. AD为⊙O的直径,PD为⊙O的切线,PCB为⊙O 的割线,PO分别交AB、AC于点M、N.求证：OM＝ON.(提示：过点C作PM的平行线分别交AB、AD于点E、F.过O作BP的垂线,G为垂足.AB∥GF.)第二讲巧添辅助妙解竞赛题在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路.1、挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化.1.1 作出三角形的外接圆例1 如图1,在△ABC中,AB＝AC,D是底边BC上一点,E是线段AD上一点且∠BED＝2∠CED＝∠A.求证：BD＝2CD.分析：关键是寻求∠BED＝2∠CED与结论的联系.容易想到作∠BED的平分线,但因BE≠ED,故不能直接证出BD＝2CD.若延长AD交△ABC的外接圆于F,则可得EB＝EF,从而获取.ABGCDFE图1证明：如图1,延长AD 与△ABC 的外接圆相交于点F,连结CF 与BF,则∠BFA＝∠BCA＝∠ABC＝∠AFC,即∠BFD＝∠CFD.故BF:CF ＝BD:DC.又∠BE F ＝∠BAC,∠BFE＝∠BCA,从而∠FBE＝∠ABC＝∠ACB＝∠BFE.故EB ＝EF. 作∠BEF 的平分线交BF 于G,则BG ＝GF.因∠GEF＝21∠BEF＝∠CEF,∠GFE＝∠CFE,故△FEG≌△FEC.从而GF ＝FC.于是,BF ＝2CF.故BD ＝2CD.1.2 利用四点共圆例2 凸四边形ABCD 中,∠ABC＝60°,∠BAD＝∠BCD＝90°,AB ＝2,CD ＝1,对角线AC 、BD 交于点O,如图2.则sin∠AOB＝____.分析：由∠BAD＝∠BCD＝90°可知A 、B 、C 、D 四点共圆,欲求sin∠AOB,联想到托勒密定理,只须求出BC 、AD 即可.解：因∠BAD＝∠BCD＝90°,故A 、B 、C 、D 四点共圆.延长BA 、CD 交于P,则∠ADP＝∠ABC＝60°. 设AD ＝x,有AP ＝3x,DP ＝2x.由割线定理得(2＋3x)3x ＝2x(1＋2x).解得AD ＝x ＝23－2,BC ＝21BP ＝4－3. 由托勒密定理有 BD·CA＝(4－3)(23－2)＋2×1＝103－12.A B C D P O 图2又SABCD ＝S△ABD＋S△BCD＝233. 故sin∠AOB＝263615 . 例3 已知：如图3,AB ＝BC ＝CA ＝AD,AH⊥CD 于H,CP⊥BC,CP 交AH于P.求证：△ABC 的面积S ＝43AP·BD. 分析：因S△ABC＝43BC2＝43AC·BC,只须证AC·BC＝AP·BD,转化为证△APC∽△BCD.这由A 、B 、C 、Q 四点共圆易证(Q 为BD 与AH 交点).证明：记BD 与AH 交于点Q,则由AC ＝AD,AH⊥CD 得∠ACQ＝∠ADQ.又AB ＝AD,故∠ADQ＝∠ABQ.从而,∠ABQ＝∠ACQ.可知A 、B 、C 、Q 四点共圆.∵∠APC＝90°＋∠PCH＝∠BCD,∠CBQ＝∠CAQ, ∴△APC∽△BCD.∴AC·BC＝AP·BD.于是,S ＝43AC·BC＝43AP·BD. 2 、构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决.2.1 联想圆的定义构造辅助圆A 图3B P Q DH C例4 如图4,四边形ABCD 中,AB∥CD,AD＝DC ＝DB ＝p,BC ＝q.求对角线AC 的长.分析：由“AD＝DC ＝DB ＝p”可知A 、B 、C 在半径为p 的⊙D 上.利用圆的性质即可找到AC 与p 、q 的关系. 解：延长CD 交半径为p 的⊙D 于E 点,连结AE.显然A 、B 、C 在⊙D 上.∵AB∥CD,∴BC＝AE. 从而,BC ＝AE ＝q.在△ACE 中,∠CAE＝90°,CE＝2p,AE ＝q,故AC ＝22AE CE -＝224q p -.2.2 联想直径的性质构造辅助圆例5 已知抛物线y ＝－x2＋2x ＋8与x 轴交于B 、C 两点，点D 平分BC.若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____. 分析：由“∠BAC 为锐角”可知点A 在以定线段BC 为直径的圆外,又点A 在x 轴上侧,从而可确定动点的范围,进而确定AD 的取值范围.解：如图5,所给抛物线的顶点为A0(1,9),对称轴为＝1,与x 轴交于两点B(－2,0)、C(4,0). 分别以BC 、DA 均交于两点P(1－22,1)、Q(1＋22,1).可知,点A 在不含端点的抛物线PA0Q 内时,∠BAC＜90°.且有3＝DP ＝DQ ＜AD≤DA0＝9,即AD 的取值范围是3＜AD≤9. A E D C B图4图52.3 联想圆幂定理构造辅助圆例6AD 是Rt△ABC 斜边BC 上的高,∠B 的平行线交AD 于M,交AC 于N.求证：AB2－AN2＝BM·BN. 分析：因AB2－AN2＝(AB ＋AN)(AB －AN)＝BM·BN,而由题设易知AM ＝AN,联想割线定理,构造辅助圆即可证得结论.证明：如图6,∵∠2＋∠3＝∠4＋∠5＝90°, 又∠3＝∠4,∠1＝∠5,∴∠1＝∠2.从而,AM ＝AN. 以AM 长为半径作⊙A,交AB 于F,交BA 的延长线于E.则AE ＝AF ＝AN.由割线定理有BM·BN＝BF·BE＝(AB ＋AE)(AB －AF)＝(AB ＋AN)(AB －AN)＝AB2－AN2,即 AB2－AN2＝BM·BN.例7 如图7,ABCD是⊙O 的内接四边形,延长AB 和DC 相交于E,延长AB 和DC 相交于E,延长AD 和BC 相交于F,EP 和FQ 分别切⊙O 于P 、Q.求证：EP2＋FQ2＝EF2.分析：因EP 和FQ 是⊙O 的切线,由结论联想到切割线定理,构造辅助圆使EP 、FQ 向EF 转化.证明：如图7,作△BCE 的外接圆交EF 于G,连结CG. 因∠FDC＝∠ABC＝∠CGE,故F 、D 、C 、G 四点共圆.由切割线定理,有EF2＝(EG ＋GF)·EF ＝EG·EF＋GF·EF＝EC·ED＋FC·FB＝EC·ED＋FC·FB＝EP2＋FQ2,即 EP2＋FQ2＝EF2.2.4 联想托勒密定理构造辅助圆 E A NC D BF M 12345图6例8 如图8,△ABC 与△A＇B ＇C ＇的三边分别为a 、b 、c 与a ＇、b ＇、c ＇,且∠B＝∠B＇,∠A＋∠A＇＝180°.试证：aa ＇＝bb ＇＋cc ＇.分析：因∠B＝∠B＇,∠A＋∠A＇＝180°,由结论联想到托勒密定理,构造圆内接四边形加以证明.证明：作△ABC 的外接圆,过C 作CD∥AB 交圆于D,连结AD 和BD,如图9所示.∵∠A＋∠A＇＝180°＝∠A＋∠D,∠BCD＝∠B＝∠B＇,∴∠A＇＝∠D,∠B＇＝∠BCD.∴△A＇B ＇C ＇∽△DCB. 有DC B A ''＝CB C B ''＝DBC A '', 即 DC c '＝a a '＝DB b '. 故DC ＝''a ac ,DB ＝''a ab . 又AB∥DC,可知BD ＝AC ＝b,BC ＝AD ＝a.从而,由托勒密定理,得AD·BC＝AB·DC＋AC·BD,即 a2＝c·''a ac ＋b·''a ab . 故aa ＇＝bb ＇＋cc ＇.练习题1. 作一个辅助圆证明：△ABC 中,若AD 平分∠A,则AC AB ＝DC BD . (提示：不妨设AB≥AC,作△ADC 的外接圆交AB 于E,证△ABC∽△DBE,从而AC AB ＝DE BD ＝DCBD .) 2. 已知凸五边形ABCDE 中,∠BAE＝3a,BC ＝CD ＝DE,∠BCD ＝∠CDE＝180°－2a.求证：∠BAC＝∠CAD＝∠DAE.(1)(2)图8A B C A'B'C'c a b a'c'b'A B CD a b b c 图9(提示：由已知证明∠BCE＝∠BDE＝180°－3a,从而A 、B 、C 、D 、E 共圆,得∠BAC＝∠CAD＝∠DAE.)3. 在△ABC 中AB ＝BC,∠ABC＝20°,在AB 边上取一点M,使BM ＝AC.求∠AMC 的度数.(提示：以BC 为边在△ABC 外作正△KBC,连结KM,证B 、M 、C 共圆,从而∠BCM＝21∠BKM＝10°,得∠AMC＝30°.)4．如图10,AC 是ABCD 较长的对角线,过C 作CF⊥AF,CE⊥AE.求证：AB·AE＋AD·AF＝AC2.(提示：分别以BC 和CD 为直径作圆交AC 于点G 、H.则CG ＝AH,由割线定理可证得结论.)5. 如图11.已知⊙O1和⊙O2相交于A 、B,直线 CD 过A 交⊙O1和⊙O2于C 、D,且AC ＝AD,EC 、ED 分别切两圆于C 、D.求证：AC2＝AB·AE.(提示：作△BCD 的外接圆⊙O3,延长BA 交⊙O3于F,证E 在⊙O3上,得△ACE≌△ADF,从而AE ＝AF,由相交弦定理即得结论.)6．已知E 是△ABC 的外接圆之劣弧BC 的中点.求证：AB·AC＝AE2－BE2.(提示：以BE 为半径作辅助圆⊙E,交AE 及其延长线于N 、M,由△ANC∽△ABM 证AB·AC＝AN·AM.)7. 若正五边形ABCDE 的边长为a,对角线长为b,试证：a b －b a＝1.(提示：证b2＝a2＋ab,联想托勒密定理作出五边形的外接圆即可证得.)FD AE C图10图11第三讲 点共线、线共点在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用。

平面几何问题选讲贾广素编著初等平面几何学初等几何学包括平面几何、立体几何与解析几何，这三部分的题目类型对于竞赛选手来讲都是非常重要的，后二者常出现在一试题目中，特别是解析几何学在最近几年的竞赛试题一试中每年都会出一道题目；而平面几何对于想在全国竞赛中想拿成绩的同学来讲，也是非常重要的，因为每年的二试（加试）试题中都会出现一道平面几何题（50分），并且是二试中最简单的一题，这当然中不能放弃的。

由于立体几何与解析几何不仅是竞赛的重点，也是我们高中学习阶段高考所重点考查的内容，练习的比较多了，平面几何我们却丢掉了，因此在这里我们着重讲这平面几何。

首先我们先介绍平面几何中的几个重要定理：第一节1．梅涅劳斯（Menelauss ）定理如果一条直线和ABC ∆的边AB CA BC ,,或其延长线分别交于点R Q P,,，且有奇数个点在边的延长线上（如图1（1）（2）） 则1=⋅⋅RBARQA CQ PC BP 。

证明方法，请注意这四种证法。

证法一：如图所示，过点A 作直线AD//PR 交BC 的延长线于点则PB DP RB AR PD CP QA CQ ==,，故⋅⋅=⋅⋅PBDPPD CP PC BP RB AR QA CQ PC BP 若对于此定理应用正弦定理以及面积法也可得出相同的结论： 证法二（正弦定理证法）：设βα=∠=∠=∠QPB CQP BRP ,,则在BPR ∆中，有γαsin sin =RB BP ， 同理可得：αββγsin sin ,sin sin ==AQ AR CP CQ ，此三式相乘即证。

证法三（面积法）：由PRC PRB S S PC BP ∆∆=，PAQ CPQQAR CQR S S S S QA CQ ∆∆∆∆==ARPRCP PAQ QAR CPQ CQR S S S S S S ∆∆∆∆∆∆=++= RBPARPS S RB AR ∆∆=，现将上述三式相乘，即可得所证结论。

平面几何介绍中学生平面几何的基本知识平面几何是几何学的一个重要分支，其研究对象为二维平面内的图形和相应的性质。

在中学数学课程中，平面几何是一个基础和必修的内容，对学生培养逻辑思维和空间想象力有着重要作用。

本文将介绍中学生学习平面几何所需掌握的基本知识。

一、点、线、面的基本概念在平面几何中，点、线、面是最基本的构成要素。

点是没有大小和形状的，用一个大写字母表示，如A、B；线由无数个点连成，用小写字母表示，如l、m；面是由无数个点和线围成的，用大写字母表示，如平面P、Q。

学生应该了解点、线、面之间的相互关系，以及它们的性质和特点，为后续的学习打下基础。

二、基本图形的定义和性质在平面几何中，学生需要掌握一些基本图形的定义和性质，如点、线、线段、射线、角、三角形、四边形等。

以三角形为例，学生应该了解三角形是由三条线段围成的封闭图形，其内角和为180度，同时了解等边三角形、等腰三角形和直角三角形的特点和性质。

三、直线与平面的相交关系学生应该了解直线和平面的相交关系，主要包括垂直和平行两种情况。

当一条直线与平面的交线为直角时，我们称该直线垂直于平面；当一条直线与平面的交线为平行时，我们称该直线平行于平面。

学生需要通过练习，掌握判断直线与平面相交关系的方法和技巧。

四、相似和全等的概念相似和全等是平面几何中重要的概念。

相似是指两个图形形状和大小相似，对应的角度相等，但尺寸可能不同；全等是指两个图形形状和大小完全相同，对应的角度和边长皆相等。

学生需要通过比较图形的对应边长和对应角度的大小，判断是否相似或全等，并能应用相似和全等的性质解答相应问题。

五、平面几何计算问题在平面几何中，计算问题是学生需要掌握和运用的重要内容。

比如计算两点之间的距离、计算线段的中点坐标等。

此外，还需要学会运用勾股定理、正弦定理、余弦定理等数学工具解决平面几何问题。

对于中学生而言，灵活运用这些工具求解实际问题是培养数学思维和创新能力的重要途径。