解析几何与平面几何选讲

高中数学备课教案空间解析几何中的直线与平面高中数学备课教案：空间解析几何中的直线与平面一、概述在高中数学课程中，空间解析几何是一个重要的内容，其中直线与平面是基本元素。

本教案的目的是帮助教师准备空间解析几何中的直线与平面的教学，并提供一些相关的教学资源和方法。

二、前期准备1. 教学目标本节课的教学目标是让学生掌握直线与平面的基本概念和性质，理解直线和平面的方程表达形式，并能够应用相关概念解决实际问题。

2. 教学资源和准备为了帮助学生理解和掌握直线与平面的概念，教师可以准备以下教学资源：- 数学教材- 相关教学视频或动画- 合适的笔记本电脑和投影仪三、教学步骤1. 导入与概念解释教师可以通过展示一张包含直线和平面的图片来引起学生的兴趣。

然后解释直线和平面的基本概念，引导学生思考它们的性质和特点。

2. 直线的表示与方程通过示例和练习，教师可以向学生展示如何表示一个直线，并引导学生推导出直线的方程表达形式。

同时，教师可以提供一些实际应用的例子，让学生感受直线在现实生活中的应用。

3. 平面的表示与方程与直线类似，教师可以引导学生探索平面的表示方法，并引导学生推导平面的方程表达形式。

同样地，教师可以通过实际问题和应用来加深学生对平面概念的理解。

4. 直线与平面的关系教师可以通过示例和图示，向学生展示直线与平面之间的关系。

例如，一条直线可以位于平面内、与平面相交或平行于平面。

通过练习，学生可以进一步熟悉这些关系，并掌握相关解题方法。

5. 综合练习与拓展为了进一步巩固学生的学习成果，教师可以提供一些综合练习和拓展问题。

这些问题可以涉及到直线与平面的交点、夹角等高级概念，并结合实际应用场景，提高学生的解决问题的能力。

四、课堂互动与讨论在教学过程中，教师应鼓励学生积极参与课堂互动与讨论，提出问题并互相交流。

通过互动与讨论，学生可以更好地理解和应用直线与平面的相关概念，同时培养他们的逻辑思维和解决问题的能力。

五、课后作业为了巩固学生的学习成果，教师可以布置一些课后作业，包括练习题和问题解答。

空间解析几何中的曲面与平面的性质与应用空间解析几何是现代数学中的一个重要分支，其中曲面与平面的性质与应用是其核心内容之一。

曲面与平面的性质研究了它们在空间中的特点和行为，而应用则将这些性质运用到实际问题中。

本文将围绕这一主题展开讨论。

一、曲面的性质曲面可以用数学方法描述，其中最常见的是方程法和参数方程法。

方程法通过一元或多元方程或等式来表示曲面，常见的有二次曲面、高次曲面等。

参数方程法是通过一组参数方程来描述曲面，常见的有球面、柱面等。

曲面有许多重要的性质，如切平面、法线、曲率等。

曲面上的每一点都有一个唯一的切平面，该平面与该点的切线相切。

曲面上每一点的切线与曲面在该点处的法线垂直。

曲率是描述曲面弯曲程度的量，曲面的曲率越大，说明其弯曲越剧烈。

二、平面的性质平面是空间中的一个二维图形，可以由一个点和一对方向向量决定。

平面的方程可以由点法式或一般式表示。

点法式通过平面上的一点和该平面的法线来确定平面方程。

一般式通过平面上的一点及平面上的两个非平行向量来确定。

平面的性质包括平行性、垂直性和夹角等。

平行平面指的是在空间中没有交点的两个平面，它们的法线方向相同或相反。

垂直平面指的是两个平面的法线方向相互垂直。

平面之间的夹角是指两个平面上相应位置的两个向量之间的夹角。

三、曲面与平面的关系应用曲面与平面的关系有许多重要的应用。

以下是其中的两个典型案例。

1. 曲面与平面的相交问题：在实际问题中，经常会遇到曲面与平面相交的情况。

通过求解曲面与平面的交点，可以得到很多有用的信息。

例如，在计算机图形学中，我们可以通过计算射线与曲面的交点来确定曲面的可见性，从而实现逼真的渲染效果。

在建筑设计中，我们也可以通过曲面与平面的相交来计算悬浮物体的投影，从而预测建筑物在不同时间下的阴影变化。

2. 曲面与平面的切割问题：曲面与平面的相交还可以用于解决物体切割问题。

例如，在机械加工中，我们经常需要通过切割固体物体来制造所需的零件形状。

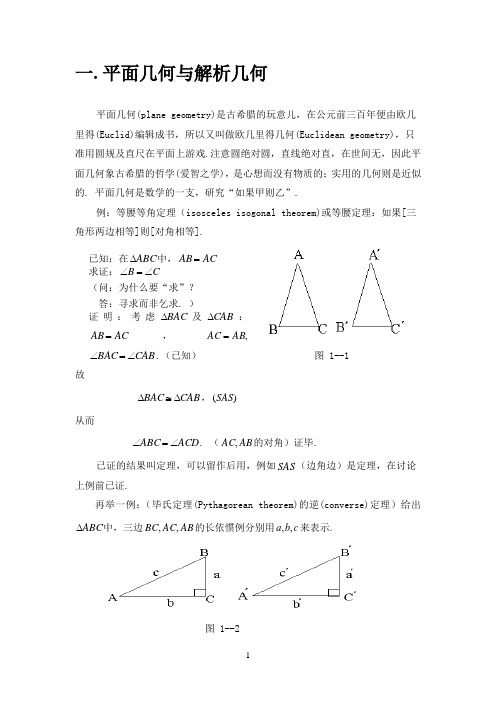
一. 平面几何与解析几何平面几何(plane geometry)是古希腊的玩意儿，在公元前三百年便由欧几里得(Euclid)编辑成书，所以又叫做欧几里得几何(Euclidean geometry)，只准用圆规及直尺在平面上游戏.注意圆绝对圆，直线绝对直，在世间无，因此平面几何象古希腊的哲学(爱智之学)，是心想而没有物质的；实用的几何则是近似的. 平面几何是数学的一支，研究“如果甲则乙”.例：等腰等角定理（isosceles isogonal theorem)或等腰定理：如果[三角形两边相等]则[对角相等].图 1--1故CABBAC∆≅∆，)(SAS从而ACDABC∠=∠. （ABAC,的对角）证毕.已证的结果叫定理，可以留作后用，例如SAS（边角边）是定理，在讨论上例前已证.再举一例：（毕氏定理(Pythagorean theorem)的逆(converse)定理）给出ABC∆中，三边ABACBC,,的长依惯例分别用cba,,来表示.图 1--2已知：在ABC∆中，ACAB=求证：CB∠=∠（问：为什么要“求”？答：寻求而非乞求. ）证明：考虑BAC∆及CAB∆：ACAB=，,ABAC=CABBAC∠=∠.（已知）已知222b a c +=. 求证：090=∠C证明：（可用余弦定理证或）作'''C B A ∆,使090=∠C ,≡'b AC C A =''， BC C B a =≡'''. 以'c 表示','B A . 因 2'2'2'b a c += （毕氏定理） 及222b a c +=， （已知） c c ='，（取代） 从而ABC ∆='''C B A ∆. )(SSS 所以=∠C 'C ∠，（对应角） 即090=∠C . (取代）证毕.毕氏为希腊人毕达哥拉斯（Pythagoras)的简译，他生于公元前五百多年 ，他的学派创立了推理法或演绎法（deduction ），用它证明了毕氏定理，由此发现了无理数（irrational number ）2：设上面的045=∠B ，且a =一单位（ 单位可任选），则2为a c. 暂设2为有理数（rational number ），即 nm=2, (1)其中n m ,为正整数.我们可以消去n m ,的公因子，即假设n m ,互质（relatively prime ）：没有大于1的（正整数）公因子. 由（1）得222m n =. (2) 两边都可以分解因子至质数，即除自己外没有大于1的因子；不计乘法的顺序，这种分解至质数积的式子是唯一的，从而由（2）知m 含因子2：k m 2=，图 1--3上面提到正整数分解为质数积的结果叫做“唯一析因定理”（unique factorization theorem ），它与物理、化学里将物分解为分子、原子……类 似.我们也可倒过来用质数积造数，例如用13,11,7造100113117=⨯⨯；这样，我们便知道将一个任意的三位数xyz 重复写，所得的六位数xyzxyz 能被13,11,7整除，而且商是xyz ！无理数的名称反映了保守派的势力.我们管毕氏定理叫勾股定理，是否也嫌 保守，忽略了希腊人创立演绎法的里程碑？问：在我们的勾股定理及四大发明后面有什么突出的方法？在它们前面又有什么远大的理想？[古印度人也会证毕氏定理:用 图 1--2作四边形AB ’C ’C, B, A ’ 在 CC ’ 內同一点. 梯形AB ’C ’C 的面积为 (b+a)(a+b)/2; 用直角三形角分算,得 ba/2+cc/2+ab/2. 故222b a c +=.]叫直角坐标(rectangular coordinates), 图 1--4一方面将平面几何化简为“代数”或解析几何（analytic geometry ）,另一方面，三维、四维、…、n 维空间的观念也自然地接踵而来：其中k 为正整数.这样(2) 可写成222k n =.再作n 的质数 因子分解，知n 也可被2整除， 与n m ,互质的假设矛盾.回顾， 除（1）外，步步有理，故（1） 不成立，即2不是有理数. 证毕.当他人沉溺于几何国中，笛卡儿（Rene ，Descartes ，1596--1650） 用两条轴来决定一点),(y x ,x 轴垂直于y 轴,n IR ≡n n a a a a a a ,......,,:),......,,{(2121是实数}n IR 表示n 维向量空间（n-dimensional vector space ）. 在n IR 中引入社会结 构数积（scalar multiplication ）、点加（pointwise addition ）及点积 （dot product ）:λ),......,,(),......,,(2121n n a a a a a a λλλ=,+),......,,(21n a a a =),......,,(21n b b b ),......,,(221n n b a b a b a +++, ⋅),......,,(21n a a a =),......,,(21n b b b n n b a b a b a +++.. (2211)其中λ,n a a a ,......,,21,n b b b ,......,,21都是实数,叫数量、纯量或标量（scalar ），n a a a ,......,,21分别是点（point ）或向量（vector ）),......,,(21n a a a 的第一、第二、…、图 1--5上面),(y x 可当作是一点P ，可当作是))0,0((=O ，也可以当作是平行移动所得的向量，叫做“自由”向量.这样当0>λ时，λ),(21a a 是向量),(21a a 的λ倍.注意+=),(21a a ),(21b b 也是物理中力向量),(21a a ,),(21b b 的和.例：求),(21c c R =的坐标,其中t =,=P ),(21a a ，=Q ),(21b b ，10<<t .第n 坐标.回到2=n ， λ),(),(2121a a a a λλ= ,+),(21a a =),(21b b ),(2211b a b a ++, ⋅),(21a a =),(21b b 2211b a b a +图 1--6解：从点P 作线平行于x 轴，交从Q R ,到x 轴的垂线于T S ,, 则PQS PRT ∆∆~，（相似） 从而图 1--7或直接用向量算：+=， 即),(),[(),(),(21212121a a b b s a a c c -+=. )1(t s -= （3） 解毕.例：求两点)3,4(),2,3(-连线的中点. 解：先推公式（4），再取21=t ，得中点的公式： s QTRSPT PS ==，（对应边比） 即,22221111s a b a c a b a c =--=-- )1(t s -= 从而)(1111a b s a c -+=, )(2222a b s a c -+=),(21),(221121b a b a c c ++=，（向量和的一半） （4） 即)21,27()32,43(21),(21-=-+=c c . 解毕.例：证明平行四边形两对角线相互平分.证：不妨设)0,0(=A ,),(21a a B =,),(21b b D =,则),(2211b a b a C ++=. 由（4）知AC 的中点是图1--8习题：在ABC ∆中，连中线AD 及在AD 上取一点G ，使GD AG 2=. 证明)(31OC OB OA OG ++=,从而证明ABC ∆三中线相交于G .图1--9=--11x x y y 1212x x y y m --=. （6）)0,0(212211++++b a b a ),(212211b a b a ++=， BD 的中点是),(212211b a b a ++ 故BD AC ,相互平分. 证毕.给出直线(straight line )L 上 的两个点),(),,(2211y x y x , 得斜率(slope ) 1212x x y y m --=（5）故L 上的任意点),(y x 的方程是图 1--10图 1--11故圆（circle ）的方程式为2121)()(y y x x -+-r =， （8） 其中),(11y x 为圆心，r 为半径. 上式可改写成：22121)()(r y y x x =-+-. （9） 例：求圆心为)2,1(，半径为3的圆的方程. 解：由（9）得2223)2()1(=-+-y x 展开，得+2x 04422=---y x y . 解毕.例：求经过两点)4,2(),1,3(-的直线的方程式.解：由（5）及（6）得 =--31x y 3214---. 化简，得或 01053=-+y x .解毕. 由毕氏定理知两点),(),,(2211y x y x 的 距离（distance ）是d ： =d 212212)()(y y x x -+- （7）在三维、四维、……、n 维空间里也可以如上玩耍.笛卡儿因发明解析几何成为现代数学的创始人. 他又是现代哲学的创始人，他的名言是：我思故我在. 想是在思考及怀疑一切、几乎失落之际迸出来的，强调怀疑与独立思考的重要性.快五十岁时他在荷兰，瑞典女皇邀他；我们不知笛卡儿瞬间的感觉，只知女皇派军舰接他上路.以后在黎明前，他为女皇讲习，如渊明为菁青.只叹当时北风凛冽如湘南的柏林，笛卡儿终于不支，患上肺炎，于次年病逝，何其浪漫！ n 维空间结果拾穗：给出向量c b a ,,，其中c b b a ⊥⊥,，即c b b a ⋅==⋅0，则,)(c b a ⊥±其中⊥读作垂直（orthogonal ）于，±表示+或-.证明：000)(=±=⋅±⋅=⋅±c b c a c b a ， 即图 1- 12注意:n 维空间不一定要有一般的几何意义，例如给出四维空间的一个点 如在相对论里 ,,(b a ),,d c ),,(c b a 可以代表一般空间的点，d 代表时间； 如在统计学里 ,,(b a ,c )d 也可以代表一个人的(高度, 重量，性别，年龄).c b a ⊥±)(. 证毕. 特例：（立体几何定理）如果PD a ≡垂直平面S ， 且S 里的DE b ≡垂直平 面S 里的OE c ≡,则PE 垂直OE .。

平面几何与解析几何平面几何和解析几何都是数学中重要的分支，它们分别从不同的角度研究几何学问题。

平面几何着重于研究二维平面上的图形和性质，而解析几何则运用代数的方法研究几何学问题。

本文将分别介绍平面几何和解析几何的基本概念和应用，以及它们之间的联系和区别。

一、平面几何平面几何是几何学的一个重要分支，它研究的对象是平面上的点、线、面及其相互之间的关系。

在平面几何中，我们研究的主要内容包括几何图形的性质、相似、全等、共线关系、垂直关系等。

1.1 点、线、面的定义与性质在平面几何中，点是最基本的概念，它没有大小和形状，只有位置。

线由无数个点连成，具有长度但没有宽度。

面由无数条线相互交织而成，具有长度和宽度。

在平面几何中，我们还研究了点、线、面的性质。

例如点到点之间可以连接成线段，线段有长度；线与线之间可以相交、平行或垂直；平面内直线和平面之间可以相交、平行或垂直。

1.2 图形的性质在平面几何中，我们研究了各种几何图形的性质。

例如，矩形的对角线相等且互相垂直；正方形的四条边相等，对角线相等且互相垂直；圆的任意一条弧都等于其半径乘以对应的角度。

1.3 相似与全等在平面几何中，我们还研究了相似和全等的概念。

两个图形相似意味着它们的形状相似但大小不同，而全等意味着它们形状和大小完全相同。

二、解析几何解析几何是代数与几何的结合，它运用了坐标系和代数的方法来研究几何学问题。

解析几何将平面几何问题转化为代数问题，通过代数运算来求解。

2.1 坐标系与点的表示在解析几何中，我们使用坐标系来表示平面上的点。

坐标系由横轴和纵轴组成，将平面分为四个象限。

每个点可以用一个有序数对(x, y)来表示，其中x表示点在横轴上的位置，y表示点在纵轴上的位置。

2.2 直线方程与曲线方程在解析几何中，我们研究了直线和曲线的方程。

通过求解方程，我们可以确定直线和曲线在平面上的位置和形状。

例如，直线的一般方程可以表示为Ax + By = C，其中A、B、C为常数；曲线的方程可以通过方程的形式来确定，例如圆的方程为(x - h)² + (y - k)² = r²，其中(h, k)表示圆心坐标，r表示半径。

空间解析几何中的直线与平面在空间解析几何中，直线和平面是两个基本的几何概念。

直线是无限延伸的一维几何体，而平面是无限延伸的二维几何体。

本文将从几何关系、方程和性质等方面介绍空间解析几何中的直线与平面。

一、直线的几何关系在三维空间中，两个不平行的直线可以有三种几何关系：相交、平行和异面，这与二维空间中直线的关系类似。

当两直线相交时，它们的交点确定了一个平面，这个平面同时包含了两个直线。

当两直线平行时，它们在无穷远处相交，但不在有限距离内相交。

而两直线异面，表示两个平面不重合。

二、平面的方程在空间解析几何中，我们可以用多种方式来表示一个平面的方程，常见的有点法式和一般式。

1. 点法式点法式是平面方程最常用的表示方法，它通过一个平面上的一点和垂直于平面的法向量来确定平面。

设平面上的一点为P(x₁, y₁, z₁)，法向量为n(a, b, c)，则点法式表示的平面方程为ax + by + cz = d。

其中d为平面与原点O的距离，可以通过将O的坐标代入方程得到。

2. 一般式一般式是通过平面上的三个点来表示平面方程，可以用于确定一个平面。

设平面上的三个点分别为A(x₁, y₁, z₁)，B(x₂, y₂, z₂)，C(x₃, y₃, z₃)，则一般式表示的平面方程为```[x - x₁ y - y₁ z - z₁][x₂ - x₁ y₂ - y₁ z₂ - z₁] = 0[x₃ - x₁ y₃ - y₁ z₃ - z₁]```其中方程中的[x, y, z]表示平面上的任意一点。

三、直线与平面的性质在空间解析几何中，直线与平面之间有一些重要的性质。

1. 直线垂直于平面当直线的方向向量与平面的法向量垂直时，我们称该直线垂直于平面。

根据向量的垂直性质，直线的方向向量与平面的法向量的数量积为零，即a₁x + b₁y + c₁z = 0。

这个方程可以表示直线的方向向量与平面的法向量的垂直关系。

2. 直线与平面的位置关系直线与平面的位置关系有三种：直线在平面上、直线与平面相交和直线与平面平行。

空间解析几何的直线与平面直线方程平面方程的求解一、直线方程的求解在空间解析几何中，直线是两点间的最短路径，它可以用直线方程来表示。

直线方程一般可以采用两种常见的形式：点向式和一般式。

1. 点向式直线方程设直线上一点为P(x,y,z)，直线的方向向量为a(i,j,k)，则该直线的点向式方程可以表示为：(x,y,z) = (x1,y1,z1) + t(i,j,k) (1)其中(x1,y1,z1)为直线上已知的一点的坐标，t为参数。

根据这个方程就可以唯一确定直线上的任意一点。

2. 一般式直线方程一般式直线方程是通过直线上的两个不重合的点的坐标来表示的。

设直线通过点P1(x1,y1,z1)和点P2(x2,y2,z2)，则一般式直线方程的表示形式为：(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1) (2)或者简化为：(x-x1)/a = (y-y1)/b = (z-z1)/c (3)其中a = x2-x1, b = y2-y1, c = z2-z1。

二、平面方程的求解平面是空间中的一个二维平面，可以用平面方程来表示。

平面方程一般可以采用三种常见的形式：一般式、点法式和截距式。

1. 一般式平面方程一般式平面方程可以表示为：Ax + By + Cz + D = 0 (4)其中A、B、C为平面的法向量的分量，D为常数。

一般式平面方程中的法向量可以通过已知法向量的坐标和平面上的一点来确定。

2. 点法式平面方程设平面上一点为P(x,y,z)，平面的法向量为n(A,B,C)，则点法式平面方程可以表示为：n · (P-P0) = 0 (5)其中·表示点乘运算，P0为平面上已知的一点的坐标。

3. 截距式平面方程截距式平面方程可以表示为：x/a + y/b + z/c = 1 (6)其中a、b、c为平面在坐标轴上的截距。

三、直线与平面方程的求解在空间解析几何中，求解直线与平面的交点，可以通过将直线方程代入平面方程，得到交点的坐标。

空间解析几何中的直线与平面在空间解析几何中，直线和平面是两个重要的几何概念，它们在我们的日常生活和各个领域都有广泛的应用。

本文将对空间解析几何中的直线与平面进行分析和探讨。

一、直线的解析表示与性质直线是由无限多个点组成的，在空间中没有宽度和厚度。

直线可以通过两个不同的点来确定，也可以通过一个点和一个方向向量来确定。

直线的解析表示通常使用参数方程或者对称式方程。

参数方程的形式为：x = x0 + aty = y0 + btz = z0 + ct其中(x0, y0, z0)是直线上的一点，(a, b, c)是直线的方向向量，t是参数。

通过改变参数t的取值可以得到直线上的所有点。

直线的性质包括长度、方向、倾斜角等。

直线的长度可以通过两点之间的距离来计算，方向可以通过方向向量来描述，倾斜角可以通过方向向量与坐标轴的夹角来计算。

二、平面的解析表示与性质平面是由无限多个点组成的二维几何图形，它有无限多个方向。

平面可以通过三个不共线的点来确定，也可以通过一个点和两个不平行的向量来确定。

平面的解析表示通常使用一般式方程或者点法式方程。

一般式方程的形式为：Ax + By + Cz + D = 0其中A、B、C是平面的法向量的分量，D是一个常数。

点法式方程的形式为：r · n = d其中r是平面上的一点的位置矢量，n是平面的法向量，d是一个常数。

通过这两种方程形式可以确定平面上的所有点。

平面的性质包括法向量、倾斜角、与其他平面或直线的交点等。

平面的法向量可以通过一般式方程的系数来确定，倾斜角可以通过法向量与坐标轴的夹角来计算，与其他平面或直线的交点可以通过方程组来求解。

三、直线与平面的关系直线与平面可以相交、平行或者重合。

当直线与平面相交时，它们的交点可以通过求解方程组来确定。

当直线与平面平行时，它们的方向向量和法向量平行。

当直线包含在平面内时，它们的方向向量和法向量垂直。

直线与平面的关系可以通过向量的内积来判断。