九年级数学平面几何中的定值问题例题讲解

初三数学讲义 专题探究：定值类问题教学过程：一、教学衔接（课前环节）1、回收上次课的教案，了解家长的反馈意见；2、检查学生的作业，及时指点3、捕捉学生的思想动态和了解学生的本周学校的学习内容二、知识点解析在几何问题中，当一些几何元素按照一定的规律在确定的范围内变化时,与它相关另一些几何元素的某些量或其数量关系保持不变，这种几何问题称之为几何定值问题. 定值问题由于所求证的问题不明确、具体,而使人难已下手,给问题解决带来困难.近年来,该类问题在各省市中考试题中频频出现,为便于广大师生复习教学,现对其归类例析.一、线段长度为定值例1如图，在半径为6，圆心角为90°的扇形OAB 的弧AB 上，有一个动点P ，PH ⊥OA ，垂足为H ，△OPH 的重心为G 。

（1）当点P 在弧AB 上运动时，线段GO 、GP 、GH 中，有无长度保持不变的线段？如果有，请指出这样的线段，并求出相应的长度；（2）设PH ＝，GP ＝，求关于的函数解析式，并写出函数的定义域； （3）如果△PGH 是等腰三角形，试求出线段PH 的长。

分析:解决此题时,首先要根据线段GH 的特征,添出辅助线,找出与其有关的长度为定值的线段间的联系,从而获得问题的解决.图一BOAGPHE二、线段长度为定值例 在给定的梯形ABCD 中，AD ∥BC ，E 是AB 边上的动点，点1O 、2O 分别是AED ∆和BEC ∆的外心。

求证：21O O 的长为一定值。

变式练习 如图，在ABC ∆中，A ∠与底边BC 为一定值，BD ⊥AC ，CE ⊥AB ，D 、E 为垂足，连结DE 。

求证：DE 为定长。

三、角的度数为定值例 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足。

求证：不管ST 滑到什么位置，SPM ∠是一定角。

ACB DEEDABCPM A O BS T例题．（2010广东广州，24，14分）如图，⊙O 的半径为1，点P 是⊙O 上一点，弦AB 垂直平分线段OP ，点D 是 APB 上任一点（与端点A 、B 不重合），DE ⊥AB 于点E ，以点D 为圆心、DE 长为半径作⊙D ，分别过点A 、B 作⊙D 的切线，两条切线相交于点C ．（1）求弦AB 的长；（2）判断∠ACB 是否为定值，若是，求出∠ACB 的大小；否则，请说明理由； （3）记△ABC 的面积为S ，若2SDE ＝43，求△ABC 的周长.四、面积为定值例. 如图7(1),正方形ABCD 的对角线相交于点O ，O 是正方形A'B'C'O 的一个顶点,如果两个正方形的边长为a,求证：正方形A'B'C'O 绕点O 无论怎样转动，两个正方形重叠部分的面积总是一个定值.CP DOBAEFE 图10图9C'B'A'C'B'A'OBDBDAC C A真题练习1．（2011•广州）已知关于x的二次函数y=ax2＋bx＋c（a＞0）的图象经过点C（0，1），且与x轴交于不同的两点A、B，点A的坐标是（1，0）（1）求c的值；（2）求a的取值范围；（3）该二次函数的图象与直线y=1交于C、D两点，设A、B、C、D四点构成的四边形的对角线相交于点P，记△PCD的面积为S1，△PAB的面积为S2，当0＜a＜1时，求证：S1－S2为常数，并求出该常数．2．（2011•河北）如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P，已知矩形ABCD的三个顶点为 A（1，0），B（1，－5），D（4，0）．（1）求c，b（用含t的代数式表示）：（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP 的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，要S=218错误！未找到引用源。

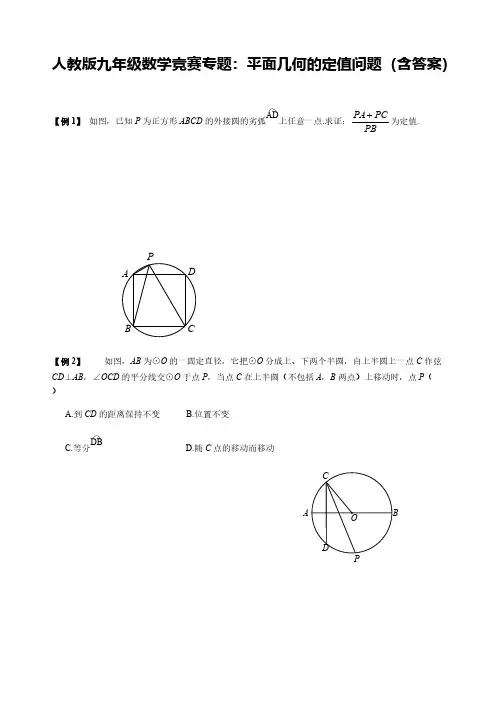
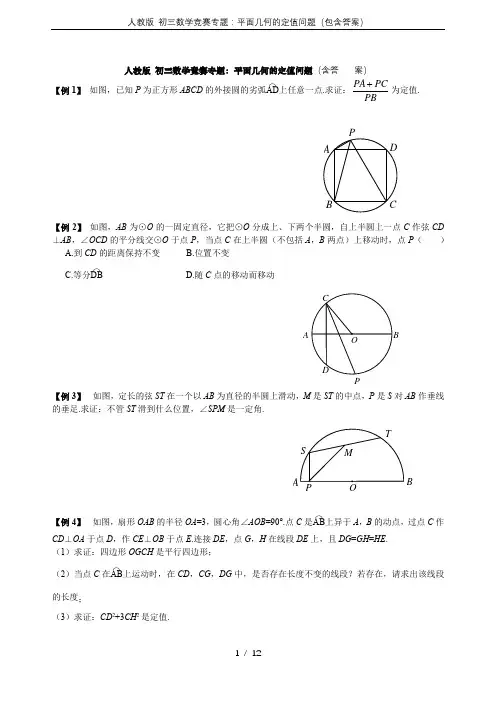
人教版 初三数学竞赛专题：平面几何的定值问题（含答案）【例1】 如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值.【例2】 如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （ ） A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.【例4】 如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律.（图1）（图2）【例6】 如图，已知等边△ABC 内接于半径为1的圆O ，P 是⊙O 上的任意一点.求证：P A 2+PB 2+PC 2为定值.【能力训练】1.如图，点A ，B 是双曲线xy 3上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则BOACE HG D A=+21S S _______.（第1题图） （第3题图） （第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA ，OB 是⊙O 任意两条半径，过B 作BE ⊥OA 于E ，又作OP ⊥AB 于P ，则定值OP 2+EP 2为_________.4.如图，在菱形ABCD 中，∠ABC =120°，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ，则直线BF 与直线DE 所夹的锐角的度数为（ ）A.30°B.40°C.50°D.60°5.如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作A A '⊥AB ，AB B B ⊥'，且A A '=AP ，B B '=BP .连接B A ''，当点P 从点A 移动到点B 时，B A ''的中点的位置（ ） A ．在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动（第5题图） （第6题图） 6.如图，A ，B 是函数xky =图象上的两点，点C ，D ，E ，F 分别在坐标轴上，且分别与点A ，B ，O 构成正方形和长方形.若正方形OCAD 的面积为6，则长方形OEBF 的面积是（ ） A.3 B.6 C.9 D.127.（1）经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ，B 和C ，D 四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A ，PB ，PC ，PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O 在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y =于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.⑥⑤④③②①P(B )A PB9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图） （第10题图）（第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证： （1）2222DK CK BK AK +++是定值； （2）2222DA CD BC AB +++是定值.11.如图，设P 是正方形ABCD 外接圆劣弧弧AB 上的一点，求证：DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2，H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时，面积S △ABC ·S △HBC 的值保持不变，则S △ABC ·S △HBC =________.2.已知A ，B ，C ，D ，E 是反比例函数xy 16=（x ＞0）图象上五个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是__________（用含π的代数式表示）.P D CB A A折叠，使点A ，B 落在六边形ABCDEF 的内部，记∠C ＋∠D ＋ ）A. ∠1＋∠2＝900°－2α B. ∠1＋∠2＝1080°－2α C. ∠1＋∠2＝720°－α D. ∠1＋∠2＝360°－21α（第3题图） （第4题图）4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在AB 上滚动，切点为T ，⊙O 交AO ，BO 于M ，N ，则弧MTN （ ）A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图，AB 是⊙O 的直径，且AB =10，弦MN 的长为8.若MN 的两端在圆上滑动时，始终与AB 相交，记点A ，B 到MN 的距离分别为h 1，h 2，则∣h 1-h 2∣等于（ ）A.5B.6C.7D.8（第5题图） 12GF EDCHBAB6.如图，已知△ABC 为直角三角形，∠ACB =90°，AC =BC ，点A ，C 在x 轴上，点B 坐标为（3，m ）（m ＞0），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B ，D . （1）求点A 的坐标（用m 表示） （2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连接PQ 并延长交BC 于点E ，连接BQ 并延长交AC 于点F .试证明：FC （AC +EC ）为定值.7.如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A ，B 的点M .设直线AC 与BM 相交于K ，直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.（第7题图） （第8题图）8.如图，设H 是等腰三角形ABC 两条高的交点，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积S △ABC ·S △HBC 的值变小、变大，还是不变？证明你的结论.9.如图，在平面直角坐标系xOy 中，抛物线10941812--=x x y 与x 轴的交点为点A ，与y 轴的交点为点B .过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC .现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时，点Q 也同时停止运动.线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于E ，射线QE 交x 轴于点F .设动点P ，Q 移动的时间为t （单位：秒）. （1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程； （3）当290<<t 时，△PQF 的面积是否总是定值？若是，求出此值；若不是，请说明理由； （4）当t 为何值时，△PQF 为等腰三角形，请写出解答过程.NKMB AC HCBA（第9题图） （第10题图） 10.已知抛物线C 1：12121+-=x x y ，点F （1,1）. （1）求抛物线C 1的顶点坐标；（2）若抛物线C 1与y 轴的交点为A ，连接AF ，并延长交抛物线C 1于点B ，求证：211=+BFAF . （3）抛物线C 1上任意一点P （x P ，y P ）（0＜x P ＜1），连接PF ，并延长交抛物线C 1于点 Q （x Q ，y Q ），试判断211=+QFPF 是否成立？请说明理由.11.已知A ，B 是平面上的两个顶点，C 是位于AB 一侧的一个动点，分别以AC ，BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证：不论C 在直线AB 同一侧的任何位置，EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ，使CE ＝AP ，连结BE ，则△BCE ≌△BAP ，及△PBE 为等腰直角三角形，故PA PC CE PC PEPB PB PB++=== 例2 B 提示：连结AC ，BC ，可以证明P 为APB 的中点． 例3 ∵SP ⊥OP ，OM ⊥ST ，∴S ，M ，O ，P 四点共圆，于是∠SPM ＝∠SOM ＝12∠SOT 为定角． 例4 (1)连结OC 交DE 于M ，则OM ＝CM ， EM ＝DM ，而DG ＝ HE ，则HM ＝GM 故四边形OGCH 是平行四边形． (2)DG 不变．DE ＝OC ＝OA ＝3 .DG ＝13DE ＝13×3＝1． (3)设CD ＝x ，延长OG 交CD 于N ，则CN ＝DN ＝12 x ，229CE x =- ， 2214DN x = .∴22394ON x =-，而ON ＝32CH ，∴22143CH x =-．故CD 2＋3CH 2＝x 2＋3(4－13x 2)＝x 2＋12－x 2为定值． 例5 ⑴C (0，4) ⑵先求得AM ＝CM ＝5，连接MC 交AE 于N ，由△AO G ∽△ANM ，得OG AO MN AN =，O G ＝32，38OG OM OC OB ==，又∠BOC ＝∠G OM ，∴△G OM ∽△COB ，∠G MO ＝∠CBO ，得M G ∥BC ．⑶连结DM ，则DM ⊥PD ，DO ⊥PM ，DO 2＝OM •OP ，OP ＝163．动点F 在⊙M 的圆周上运动时，从特殊位置探求OFPF的值．当F 与点A 重合时，2316523OF AO PF AP ===-；当点F 与点B 重合时，8316583OF OB PF PB ===+；当点F 不与点A ，B 重合时，连接OF 、PF 、MF ，∴DM 2＝MO •MP ，∴FM 2＝MO •MP ，即FM MPOM FM=，又∠OMP ＝∠FMP ，∴△MFO ∽△MPF ，35OF MO PF MF ==，故OF PF 的比值不变，比值为35． 例6 ∠BPC ＝120°，在△BPC 中，由余弦定理得BC 2＝PB 2＋PC 2－2PB •PC ＝BC 2，又由上托勒密定理得BC •P A ＋PC •AB ，而AB ＝BC ＝AC ，∴P A ＝PB ＋PC ，从而P A 2＋ PB 2＋ PC 2＝ (PB ＋PC )2＋ PB 2＋ PC 2＝2 (PB 2＋PC 2＋PB •PC )＝2BC 2＝2×()23＝6．故P A 2＋PB 2＋PC 2为定值．A 级 1．4提示：∵S 1＋S 阴＝ S 2＋S 阴＝xy ＝3，∴S 1＋S 2＝2xy －2S 阴＝6－2＝4．2．273 提示：1＋3＋5＝9是等边三角形的高． 3．r 2提示：先考查OB 与OA 垂直的情形．4．D 提示：延长BF 交DE 于点M ，连接BD ，则△BCD 为等边三角形，BF 平分∠CBD ．∵F 为CD 中点，且AD ∥CE ，∴△ADF 与△ECF 关于点F 中心对称．∴CE ＝AD ＝CD ，∴∠CEM=30°，∠DMF=60°，5．D 提示：A′B′的中点均在⊙O 的上半圆的中点处． 6．B 提示：S 正方形OCAD ＝OD •OC ＝A A x y k =＝6，∴S OEBF ＝OE •OF ＝x B •y B k =＝6． 7．⑴略⑵当点P在⊙O 内时，过P 作直径CD ，则PE •PF ＝PD •PC ＝r 2－OP 2为定值；当点P 在⊙O 外时，PE •PF 为定值22OP r -．结论：过不在圆上的一个定点任作一条直线与圆相交，则这点到直线与圆相交点的两条线段长的积为定值． 8．⑴2π⑵22.5° ⑶P 值无变化．理由如下：如图，延长BA 交y 轴于E 点，可证明△OAE ≌△OCN ，得OE ＝ON ，AE ＝CN ，又∠MOE ＝∠MON ＝45°，OM ＝ON ，∴△OME ≌△OMN ，得MN ＝ME ＝AM ＋AE ＝AM ＋CN ．∴P ＝MN ＋BN ＋BM ＝AM ＋CM ＋CN ＋BN ＋BM ＝AB ＋AC ＝4．9．⑴0＜x ＜90 ⑵BE ＝BF 提示：连接BD ，可证明△BDF ∽△ADB ，△BDE ∽△ADC ． 10．⑴作OP ⊥BD 于P ，OQ ⊥AC 于Q ，连接AO ，则AO 2＝()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦，又AK •CK ＝BK •DK ，得AK 2＋BK 2＋CK 2＋DK 2＝4R 2为定值． ⑵作直径DE ，连接AE ，BE ，CE ，AB 2＋CD 2＝4R 2，AD 2＋BC 2＝4R 2，故AB 2＋BC 2＋CD 2＋DA 2＝8K 2为定值． 11．设正方形的边长为a ，根据托勒密定理，对于四边形APBC 和四边形APBD ，有CP •a ＝AP •a ＋BP •2a ，DP •a ＝BP •a ＋AP •2a ，两式相加并整理得(CP ＋DP )a ＝(AP ＋BP )(a ＋2a )，从而21AP BPCP DP+=-+为定值．B 级1．1 提示：不妨设∠A 为锐角，AD ，BE ，CF 为△ABC 的三条高，H 为垂心，由AB ＝AC 知∠HBD ＝∠HCD ＝∠HAE ，∠HDC ＝∠CDA ＝90°，故R t △CHD ∽R t △ACD ．∴AD DC DC HD =，即AD •HD ＝DC 2＝14BC 2＝1．∴S △ABC •S △HBC ＝2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭＝1．当∠A ≥90°时，结论成立．2．13π－26 提示：∵A ，B ，C ，DE 是反比例函数y ＝16x(x ＞0)图象上五个整数点，由图象可知，这些点的横坐标分别为1，2，4，8，16．∴五个正方形的边长分别为1，3，4，2，1．∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦＝5π－10＋8π－16＝13π－26． 3．B 提示：如图，设F A 的延长线与CB 的延长线交于点P ，G A ′的延长线与HB ′的延长线交于点P ′．由对称性可知∠1＝2∠APP ′，∠2＝2∠BPP ′．∴∠1＋∠2＝2∠APB ．∵∠APB ＝540°－α，∴∠1＋∠2＝1080°－2α． 4．D 5．B 提示：如图，设AB 与MN 交于点C ，过点O 作OD ⊥MN 于D ，连接FO 并延长交EB 于G ．由垂径定理，得OD ＝2254-＝3．由△AFO ≌△B G O ，得AF ＝B G ，即h 1＝B G ．由AF ⊥MN ，BE ⊥MN ，得△FOD ∽△F G E ．∴12OD FO GE FG ==．∴E G ＝2OD ＝6，∴12h h AF BE -=-＝E G ＝6． 6．⑴A (3－m ，0) ⑵y ＝x 2－2x ＋1 ⑶过点Q 作QM ⊥AC 于M ，过点Q 作QN ⊥BC 于N ，设Q 点的坐标为(x ，x 2－2x ＋1)，则QM ＝CN ＝(x －1)2，MC ＝QN＝3－x ．∵QM ∥CE ，∴PQM ∽△PEC ．∴QM PMEC PC=，即()2112x x EC--=，得EC ＝2(x －1)．∵QN ∥CF ，∴△BQN ∽△BFC ．∴QN BN FC BC =，即()24134x x FC ---=，得FC ＝41x +．又AC ＝4，∴FC (AC ＋EC )＝()44211x x +-⎡⎤⎣⎦+＝8为定值． 7．提示：易证△ABK ∽△BNA ，故AK •BN ＝AB 2为定值，即AK 与BN 的乘积与M 点的选择无关． 8．提示：S △ABC •S △HBC ＝116BC 4，由于BC 是不变的，所以当点A 至BC 的距离变小时，乘积S △ABC •S △HBC 保持不变． 9．⑴A (18，0)，B (0，－10)，顶点坐标为(4，－989)⑵若四边形PQCA 为平行四边形，由于QC ∥P A ，故只要QC ＝P A 185． ⑶即可，而P A ＝18－4t ，CQ ＝t ，故18－4t ＝t ，得t ＝设点P 运动t s ，则OP ＝4t ，CQ ＝t ，0＜t ＜4.5．说明P在线段OA 上，且不与点O ，A 重合．由于QC ∥OP 知△QDC ∽△PDO ，故144QD QC t DP OP t ===．同理QC ∥AF ，故14QC CE AF EA ==，即14t AF =，∴AF ＝4t ＝OP ．∴PF ＝P A ＋AF ＝P A ＋OP ＝18．又点Q 到直线PF 的距离d ＝10，∴S △PQF ＝12•PF •d ＝12×18×10＝90．于是S △PQF 的面积总为定值90． ⑷由前面知道，P (4t ，0)，F (18＋4t ，0)，Q (8－t ，－10)，0≤t ≤4.5．构造直角三角形后易得PQ 2＝(4t －8＋t )2＋102＝，FQ 2＝(18＋4t －8＋t )2＋102＝(5t ＋10)2＋100．①若FP ＝FQ ，即182＝(5t ＋10)2＋100，故25(t ＋2)2＝224，(t ＋2)2＝24425．∵2≤t ＋2≤6.5，∴t ＋2＝244414255=．∴t ＝ 4145－2． ②若QP ＝QF ，即(5t －8)2＋100＝(5t ＋10)2＋100，即(5t －8)2＝(5t ＋10)2，无0≤t ≤4.5的t 满足． ③若PQ ＝PF ，即(5t －8)2＋100＝182，∴(5t －8)2＝224．由于224≈15，又0≤5t ≤22.5，∴－8≤5t －8≤14.5，14.52＝22984124⎛⎫= ⎪⎝⎭＜224．故没有t (0≤t ≤4.5)满足此方程．综上所述，当t ＝4145－2时，△PQ R 为等腰三角形． 10．⑴C 1的顶点坐标为(1，12). ⑵略 ⑶作PM ⊥AB 于M ，作QN ⊥AB 交AB 延长线于N ，∴PM ＝1－y P ，FM ＝1－x P ．在R t △PMF 中，PF 2＝(1－y P )2＋(1－x P )2＝1－2y P ＋y P 2＋1－2x P ＋x P 2，又∵点P 在抛物线上，∴y P ＝12x P 2－x P ＋1，∴PF 2＝1－x P 2＋2x P －2＋y P 2＋1－2x P ＋x P 2＝y P 2，∴PF ＝y P ，同理，QF ＝y Q ，易证△PMF ∽△QNF ，则PM QN PF QF =，∴11Q P y y PF QF --=，即11PF QF PF QF --=，∴11PF QF+＝2． 11．先从特殊情况出发．当△ABC 是等腰直角三角形时，点P 与点C 重合，此时点P 的位置在AB 的中垂线上，且到AB的距离为12AB ，如图①所示．下面就一般情况来证明上面的结论(结论②所示)．过C ，E ，G 分别作直线AB 的垂线CH ，EM ，G N ，垂足分别是H ，M ，N ．容易证明△AEM ≌△ACH ，△B G N ≌△BCH ．从而有AM ＝CH ＝BN ，EM ＝AH ，G N ＝BH ．这样，线段AB 的中点O 也是线段MN 的中点，连接OP ，则OP 是梯形EMN G 的中位线，从而OP ⊥AB ，OP ＝12(EM ＋G N )＝ 12(AH ＋BH )＝12AB ．∴无论点C 在AB 同一侧的位置如何，E G 中点P 的位置不变．。

专题04 解析几何中的定值问题常见考点考点一 定值问题典例1．已知抛物线2:2(0)C x py p =>的焦点为F ，点()0,4P x 是抛物线C 上一点，6PF =． (1)求抛物线C 的方程；(2)过()0,4Q 的直线l 与抛物线C 相交于A ，B 两点，求证：2211||||AQ BQ +为定值． 【答案】(1)28x y = (2)证明见解析 【解析】 【分析】（1）由6PF =，根据抛物线的定义得到462p+=，求得4p =，即可求得抛物线的方程； （2）设直线l 的方程为4y kx =+，联立方程组利用韦达定理12128,32x x k x x +==-，结合两点距离公式，化简21212222212()2111||||1()x x x x AQ BQ k x x +-+=⋅+，代入即可求解. (1)解：因为点()0,4P x 在抛物线2:2C x py =上，且6PF =， 由抛物线的定义可得462pPF =+=，解得4p =， 所以抛物线的方程为28x y =. (2)解：设直线l 的斜率为k ，可得直线l 的方程为4y kx =+， 联立方程组248y kx x y=+⎧⎨=⎩，整理得28320x kx --=， 设1122(,),(,)A x y B x y ，可得2(8)4(32)0k ∆=-⨯->且12128,32x x k x x +==-， 由222222222211221122111111||||(4)(4)(44)(44)AQ BQ x y x y x kx x kx +=+=++-+-++-++- 22212121222222222121212()21111(1)(1)1()1()x x x x x x k x k x k x x k x x ++-=+=⋅=⋅++++ 222221(8)2(32)1111(32)11616k k k k -⨯-+=⋅=⋅=+-+.变式1-1．已知椭圆C ：22221(0)x y a b a b +=>>的短轴长为2设点()(),00,M m m m a ≠≠±是x 轴上的定点，直线l ：222a mx m+=，设过点M 的直线与椭圆相交于A 、B 两点，A 、B 在l 上的射影分别为A '、B '． (1)求椭圆C 的方程；(2)判断AA BB '⋅'是否为定值，若是定值，求出该定值；若不是定值，请说明理由．【答案】(1)2214x y +=；(2)是定值，定值为222(4)4m m -.【解析】 【分析】(1)根据题意列方程得出a ，b 的值即可得出椭圆方程；(2)求出当直线AB 斜率为0时AA BB '⋅'的值，再求当直线AB 斜率不为零或不存在时AA BB '⋅'的值.当直线AB 斜率不为零或不存在时，设直线AB 方程为x ky m =+，和椭圆方程联立，根据韦达定理计算AA BB '⋅'.由此即可得出结论． (1)由题意可知1b =，ca=又222a c b -=，2a ∴=，1b =，c∴椭圆的标准方程为：2214x y +=；(2)当直线AB 斜率为0时，A 、B 分别为椭圆的左右顶点，A '、B '均为22,02a m m ⎛⎫+ ⎪⎝⎭， 则222244222222222222()(4)22444a m a m a m a m a m m AA BB a a a m m m m m ++++--'⋅'=-⋅+=-==，当直线AB 斜率不为0时，设直线AB 的方程为x ky m =+，联立方程组2214x ky m x y =+⎧⎪⎨+=⎪⎩， 消去y 得：2222(4)8440k x mx m k +-+-=，设1(A x ，1)y ，2(B x ，2)y ，则0∆>时，12284mx x k +=+，22122444m k x x k -=+，222221212122444(4)()2224m m m m AA BB x x x x x x m m m m ++++''∴⋅=-⋅-=-++222222(4)(4)444m m m m +-=-+=．综上，AA BB '⋅'为定值222(4)4m m -．变式1-2．已知椭圆C ：22221x y a b+=(a ＞b ＞0)，点P （1，32）在椭圆上，且离心率e ＝12.(1)求椭圆C 的方程；(2)若椭圆C 的右焦点为F ，过B （4，0）的直线l 与椭圆C 交于D ，E 两点，求证：直线FD 与直线FE 斜率之和为定值.【答案】(1)22143x y +=(2)证明见解析 【解析】 【分析】（1）根据条件可得12c a=，然后将点31,2⎛⎫ ⎪⎝⎭代入椭圆方程求解即可；（2）设直线l 的方程为y =k (x -4)，D (x 1，y 1)，E (x 2，y 2)，然后联立椭圆与直线的方程消元，然后韦达定理可得21223234k x x k +=+，2122641234k x x k-=+，然后可算出FD FE k k +为定值. (1)由题意知，12c e a ==，所以a =2c ，22b a =-2c =23c ， 故椭圆的方程为2222143x y c c+=，又点P （1，32）在椭圆上，代入解得21c = 所以2a =4， 23b =，故椭圆C 的方程为22143x y +=.(2)设直线l 的方程为y =k (x -4)，D (x 1，y 1)，E (x 2，y 2)，联立方程组()224143y k x x y ⎧=-⎪⎨+=⎪⎩，可得()2222343264120k x k x k +-+-=，则0∆>，解得2k <14，∴21223234k x x k +=+，2122641234k x x k-=+， FDFE k k +=()121212*********(1)(1)k x x x x y y x x x x ⎡⎤-++⎣⎦+=----()()()()22222222121264123212824160243225834343401111k k k k k k k k k k x x x x ⎛⎫⎛⎫---++⨯-⨯+ ⎪⎪+++⎝⎭⎝⎭===---- 所以直线FD 与直线FE 斜率之和为0.变式1-3．如图，已知圆22:4O x y +=，点(1,0)B ，以线段AB 为直径的圆内切于圆O ，点A 的集合记为曲线C .(1)求曲线C 的方程；(2)已知直线:4l x =，3(1,)2Q ，过点B 的直线1l 与C 交于,M N 两点，与直线l 交于点K ，记,,QM QN QK 的斜率分别为123,,k k k ，问：1223k k k k --是否为定值？若是，给出证明，并求出定值；若不是，说明理由. 【答案】(1)22143x y +=(2)是定值，证明见解析，2- 【解析】 【分析】(1)按照所给的条件，分析图中的几何关系即可；(2)作图，联立方程，按步骤写出相应点的坐标，求对应的斜率即可. (1)设AB 的中点为P ，切点为Q ，连接,OP PQ ， 取B 关于y 轴的对称点D ，则2BD = ，连接AD ，由于P 是AB 的中点，O 是BD 的中点，∴=2AD OP ，故=2222AB AD OP PB OP PQ ++=+()242OP PB BD =+=>=.所以点A 的轨迹是以,B D 为焦点，长轴长为4的椭圆.其中2,1,a c b ===C 的方程为22143x y +=；(2)由第一问，作图如下：设1122(,),(,),M x y N x y 依题意，直线1l 的斜率必定存在， 设1:1(0)l x my m =+≠，将其与椭圆方程联立：221(0)143x my m x y =+≠⎧⎪⎨+=⎪⎩得22(34)690m y my ++-=， 由韦达定理，得：12122269,3434m y y y y m m --+==++ 易得点3(4,)K m ，33311232m k m -==-111113322,1y y k x my --==-22232y k my -= 133213122323231k k k k k k k k k k k k k k -+---==---- 而121213122231212112311()()3223113()()22y y m y y k k my y y m k k my y y y y m y y m -----==-----……① 由12122269,3434m y y y y m m --+==++得：12123()2y y y y m =+， 代入①得：1312223121313k k my y y k k my y y --==---，得1332131223232312k k k k k k k kk k k k k k -+---==-=----故答案为：22143x y +=，是定值，理由见解析，-2.典例2．已知椭圆1C：(22216x y a a +=>，1C 的左右焦点1F ，2F 是双曲线2C 的左右顶点，1C 的离2C，点E 在2C 上，过点E 和1F ，2F 分别作直线交椭圆1C 于F ，G 和M ，N 点，如图.(1)求1C ，2C 的方程；(2)求证：直线1EF 和2EF 的斜率之积为定值； (3)求证：11FG MN +为定值.【答案】(1)1C ：221186x y+=；1C ：221x y -=(2)证明见解析 (3)证明见解析 【解析】【分析】（1）利用待定系数法，根据条件先求曲线1C 的方程，再求曲线2C 的方程； （2）首先设()00,E x y ，表示直线1EF 和2EF 的斜率之积，即可求解定值；（3）首先表示直线1EF (1y k x =+与1C 方程联立消y ，利用韦达定理表示弦长FG ，以及利用直线1EF 和2EF 的斜率关系121k k =，表示弦长MN ，并证明11FG MN +为定值. (1)由题设知，椭圆1C =解得218a =∴()1F -，()2F∵椭圆1C 的左右焦点1F ，2F 是双曲线2C 的左右顶点， ∴设双曲线2C ：()2221012x y n n -=>∴2C =212n =.∴1C ：221186x y+=2C ：2212x y -=；(2)证明：∵点E 在2C 上 ∴设()00,E x y则220012y x =-，∴122020112EF EFy k k x ⋅==-. ∴直线1EF 和2EF 的斜率之积为定值1； (3)证明：设直线1EF 和2EF 的斜率分别为1k ，2k ，则121k k = 设()11,F x y ，()22,G x y1EF：(1y k x =+与1C 方程联立消y 得()()22221113118210kx x k +++-=“*”则1x ，2x 是“*”的二根则()121211221182131x x k x x k ⎧+=⎪⎪⎨-⎪=⎪+⎩则FG =)2121131k k ++ 同理))2222112221211111131331k k k MN k k k ⎫+⎪++⎝⎭===++⋅+∴2211FG MN+== 变式2-1．已知()2222:10x y C a ba b +=>>左、右顶点分为A ，B 点围成的四边形面积为4. (1)求椭圆C 的标准方程；(2)过点()4,0M -作直线PQ 交椭圆C 于P ，Q 两点（点P ，Q 异于A ，B ），若直线AP 和BQ 的交点为N .求证：MB AN ⋅为定值.【答案】(1)22142x y +=(2)证明见解析 【解析】 【分析】(1)根据题意和离心率求出2a =，b(2)设设()00,N x y ，()11,P x y ，()22,Q x y ，直线PQ 的方程，联立椭圆方程并消去x ，利用韦达定理表示出1212y y y y +、，根据直线的点斜式方程求出直线AP 、BQ ，结合平面向量的坐标表示化简计算即可. (1)由题意得：c e a =12242b c ⋅=，即a ，2bc =，又222a b c =+，则有2a =，b =则椭圆C 的标准方程为：22142x y +=.(2)由题意知：直线PQ 的斜率不为0， 设直线:4PQ x my =-， 由224,24,x my x y =-⎧⎨+=⎩，得()2228120m y my +-+=， 设()00,N x y ，()11,P x y ，()22,Q x y ，则()21660m ∆=->，12282m y y m +=+，122122y y m =+. 因为()2,0A -，()2,0B ，则0612MB AN x ⋅=+.则()1212212322m my y y y m ==++①， 直线()11:22y AP y x x =++②，直线()22:22y BQ y x x =--③， 由②③得：()()1200122222y yx x x x +=-+-， 则()()()()221210212210121212112222222662y y x y my x x my y y y x y x y my my y y x +-+--====----+④ 将①代入④得：()()122001213221232362y y y x x y y y+-+==--+-，则01x =-， 则06126MB AN x ⋅=+=-.变式2-2．已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ，2F ，椭圆上的点到焦点的最大距离为方程2610x x -+=的根，离心率e 满足228a e =． (1)求椭圆C 的方程；(2)若直线():0l y kx m k =+≠与椭圆C 相交于A ，B 两点，且AB 的垂直平分线过点10,2P ⎛⎫- ⎪⎝⎭，求证：2169m k -为定值．【答案】(1)2219x y +=(2)证明见解析 【解析】 【分析】（1）根据已知条件得出关于a c +的等式，结合离心率c e a=，228a e =，222a b c =+，求出a ，b 的值，即得椭圆C 的方程；（2）设()11,A x y ，()22,B x y ，将直线l 的方程与椭圆C 的方程联立，利用根与系数的关系求12x x +，12y y +的表达式，进而得到AB 的中点M 的坐标，利用直线1PM l k k ⋅=-即可证明2169m k -为定值．(1)因为方程2610x x -+=的实数根为3±①若3a c +=+228a e =，所以28c =，即c =3a =．因为222a b c =+，所以1b =，此时椭圆C 的方程为2219x y +=；②若3a c +=-228a e =，所以28c =，即c =所以30a =-<，不符合题意，所以椭圆C 的方程为2219x y +=；(2)证明：设()11,A x y ，()22,B x y ，联立221,9,x y y kx m ⎧+=⎪⎨⎪=+⎩得()2221918990k x mkx m +++-=．因为直线y kx m =+与椭圆C 相交于A ，B 两点，所以()()2222324419990m k k m ∆=-⨯+⨯->，即2291m k <+，由韦达定理知1221819mk x x k +=-+，122219my y k +=+， 所以AB 的中点229,1919mkm M k k ⎛⎫-⎪++⎝⎭．又因为AB 的中垂线过点10,2P ⎛⎫- ⎪⎝⎭，且0k ≠，所以22119219019m k k mk k ++⋅=---+， ()2222191919219m k k k mk k ⎛⎫+++⋅-⋅=- ⎪+⎝⎭，221918m k m ++=，所以21691m k -=， 所以2169m k -为定值．变式2-3．斜率为1的直线交抛物线()2:20C y px p =>于A ，B 两点，且弦AB 中点的纵坐标为2.(1)求抛物线C 的标准方程；(2)已知点()1,P m 在抛物线C 上，过点P 作两条直线PM ，PN 分别交抛物线C 于M ，N （M ，N 不同于点P ）两点，且MPN ∠的平分线与y 轴垂直，求证：MN 的斜率为定值. 【答案】(1)24y x = (2)证明见解析 【解析】 【分析】（1）利用点差法求得p ，由此求得抛物线C 的标准方程.（2）求得P 点的坐标，设出直线,PM PN 的方程，通过联立方程求得,M N 两点的坐标，进而判断MN 的斜率为定值. (1)设()()1122,,,A x y B x y ，12122,42y y y y +=+=， 21122222y px y px ⎧=⎨=⎩，两式相减并化简得1212122y y p x x y y -=-+，21,24p p ==， 所以抛物线方程为24y x =. (2)当1x =时，2414,2y y =⨯==±，所以()1,2P ±. 不妨设()1,2P ，依题意可知直线,PM PN 的斜率存在、不为0且互为相反数，设直线PM 的斜率为k ，则直线PN 的斜率为k -， 直线PM 的方程为()21,2y k x y kx k -=-=+-， 直线PN 的方程为()21,2y k x y kx k -=--=-++，224y kx k y x=+-⎧⎨=⎩，解得24441,2M k k k ⎛⎫-+- ⎪⎝⎭， 同理可求得24441,2N k k k ⎛⎫++-- ⎪⎝⎭，所以直线MN 的斜率为224482218444411k k k k k k kk ⎛⎫-----⎪⎝⎭==-⎛⎫++--+ ⎪⎝⎭，是定值.巩固练习练习一 定值问题1．已知定点()0,1F ，定直线:1m y =-，动圆M 过点F ，且与直线m 相切. (1)求动圆M 的圆心轨迹E 的方程；(2)过焦点F 的直线l 与抛物线E 交于A B ､两点，与圆22:20N x y y +-=交于C D ､两点（A ，C 在y 轴同侧），求证：AC DB ⋅是定值. 【答案】(1)24x y = (2)1 【解析】 【分析】（1）利用抛物线的定义先判定动点的轨迹形状，再求其标准方程；（2）设出直线方程，联立直线和抛物线的方程，得到关于x 的一元二次方程，利用根与系数的关系、抛物线的定义进行证明. (1)解：由题意，得动圆的圆心M 到点()0,1F 的距离等于到直线1y =-的距离，所以M 的轨迹是以点()0,1F 为焦点的抛物线，其轨迹方程为2:4E x y =；(2)解：设经过焦点F 的直线为:1l y kx =+， 联立214y kx x y=+⎧⎨=⎩，得2440x kx --=； 设11(,)A x y ，22(,)B x y ，则2=16(1)0k ∆，且124x x k +=，124x x =-；因为圆22:20N x y y +-=的圆心为()0,1N （即抛物线的焦点），半径为1， 由抛物线的定义，得1||1AF y =+，2||1BF y =+， 则1||||1AC AF y =-=，2||||1BD BF y =-=， 所以1212(1)(1)AC DB y y kx kx ⋅==++2221212()14411k x x k x x k k =+++=-++=，即AC DB ⋅是定值，定值是1.2．已知椭圆22:14x C y +=，下顶点为A ，不与坐标轴垂直的直线l 与C 交于P ，Q 两点．(1)若线段PQ 的中点为11,2⎛⎫- ⎪⎝⎭R ，求直线l 的斜率；(2)若l 与y 轴交于点(0,2)B ，直线,AP AQ 分别交x 轴于点M ，N ，求证：M ，N 的横坐标乘积为定值．【答案】(1)12； (2)证明见解析. 【解析】 【分析】（1）设1122(,),(,)P x y Q x y ，应用点差法可得121212124()y y x xx x y y -+=--+，结合PQ 的中点R 有12122,1x x y y +=-+=，即可求直线l 的斜率；（2）设直线:2l y kx =+，联立椭圆方程应用韦达定理求12x x +、12x x ，由判别式求k 的范围，进而写出直线,AP AQ 并求M ，N 坐标，化简M N x x 即可证明结论. (1)设1122(,),(,)P x y Q x y ，由,P Q 在椭圆C 上，则221122221414x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩，两式相减得12121212()()()()04x x x x y y y y -++-+=，即121212124()y y x x x x y y -+=--+，又PQ 的中点R11,2且R 在椭圆C 内，则12122,1x x y y +=-+=，所以直线l 的斜率为121212y yx x -=-．(2)由题意知，直线l 的斜率存在，设直线:2l y kx =+，1122(,),(,)P x y Q x y ，联立22214y kx x y =+⎧⎪⎨+=⎪⎩得：22(14)16120k x kx +++=． 由22(16)48(14)0k k ∆=-+>得：234k >，即k <或k >1221614k x x k -+=+，1221214x x k =+.直线AP 为1111y y x x +=-，令0y =得：111x x y =+，则11,01x M y ⎛⎫ ⎪+⎝⎭，同理得22,01x N y ⎛⎫⎪+⎝⎭， 所以121212212121212(1)(1)(3)(3)3()9M N x xx xx xy y kx kx k x x x x k x x ===+++++++22212412489(14)3k k k ==-++，所以,M N 的横坐标乘积为定值43．3．已知椭圆2222:1(0)x y E a b a b +=>>的长轴长为4，1F ，2F 为E 的左､右焦点，M 为E 上一动点，当12MF F △的面积最大时，其内切圆半径为3b.(1)求E 的标准方程：(2)过点1F 作斜率之和为3的两条直线1l ，2l ，1l 与E 交于点A ，B ，2l 与E 交于点C ，D ，线段AB ，CD 的中点分别为P ，Q ，过点1F 作1F H PQ ⊥，垂足为H .试问：是否存在定点T ，使得线段TH 的长度为定值.【答案】(1)22143x y +=；(2)存在11,8T ⎛⎫- ⎪⎝⎭，TH 为定值，证明见解析.【解析】 【分析】(1)根据内切圆的半径表示出三角形的面积，结合长轴的定义即可求出a 、b ，进而求得椭圆方程；(2)设直线PQ 的方程为y kx m =+，直线AB 的方程为1(1)y k x =+，直线CD 的方程为2(1)y k x =+，由直线PQ 和直线AB 的方程求出点P 的横坐标，直线AB 联立椭圆方程，利用韦达定理，结合题意即可求出当T 为1F G 的中点时，TH 为定值. (1)设椭圆的焦距为2c ，由12MF F △的面积最大时，其内切圆半径为3b ， 得112(22)223b c b a c ⨯⨯=+⨯，化简，得12c a=， 又24a =，所以21a c ==，，所以2223b a c =-=，故椭圆的标准方程为22143x y +=；(2)当直线PQ 的斜率不存在时，PQ x ⊥轴，点P 与点Q 关于x 轴对称， 则120k k +=，与题意中的123k k +=矛盾，不符合题意； 设直线PQ 的方程为y kx m =+，则直线AB 的方程为1(1)y k x =+，直线CD 的方程为2(1)y k x =+，由1(1)y k x y kx m=+⎧⎨=+⎩，得11P m k x k k -=-，由122(1)143y k x x y =+⎧⎪⎨+=⎪⎩，得2222111(34)84120k x k x k +++-=，设()()1122,,A x y B x y ，，则2121214234P x x k x k +==-+， 所以2121434k k -=+11m k k k --，化简得2114()330k m k k m -+-=， 同理，2224()330k m k k m -+-=，所以12k k 、为方程24()330k m x x m -+-=的两个根， 有1234()k k k m +=--，又123k k +=，所以14k m =-，所以直线PQ 的方程为111()()(1)444y m x m m x =-+=-++，得直线PQ 过定点1(1,)4G -，又1(1,0)F -，1F H PQ ⊥，所以1F H HG ⊥， 则点H 在以1F G 为直径、以1(1,)8T -为圆心的圆上， 故点H 到圆心1(1,)8T -的距离恒为定值，即存在点1(1,)8T -为1F G 的中点时，TH 为定值.4．如图，在平面直角坐标系中，12,F F 分别为双曲线()2222:10,0x y a b a bΓ-=>>的左、右焦点，双曲若点A 为双曲线右支上一点，且12AF AF -=直线2AF 交双曲线于B 点，点D 为线段1F O 的中点，延长,AD BD ，分别与双曲线Γ交于,P Q 两点.(1)若()()1122,,,A x y B x y ，求证：()1221212x y x y y y -=-； (2)若直线,AB PQ 的斜率都存在，且依次设为12,k k .试判断21k k 是否为定值，如果是，请求出21k k 的值；如果不是，请说明理由. 【答案】(1)证明见解析 (2)为定值，7 【解析】 【分析】（1）分两种情况讨论，斜率不存在时，直接验证，斜率存在时，运用斜率公式可证明；（2）设直线AD 的方程为()1111y y x x =++，与双曲线联立得111134,2323x y P x x ⎛⎫--- ⎪++⎝⎭，同理得222234,2323x y Q x x ⎛⎫--- ⎪++⎝⎭，由斜率公式及（1）中的结论可得结论. (1) 证明：由双曲线离心率ce a==12||||2AF AF a -=，及222c a b =+， 可得2222,2,4a b c ===，所以双曲线方程为22122x y -=，2(2,0)F .当直线AB 的斜率不存在时，122x x ==，()12212121222x y x y y y y y -=-=-，直线AB 的斜率存在时，22AF BF k k =，121222y yx x =--，整理得()1221212x y x y y y -=-， 综上所述，()1221212x y x y y y -=-成立； (2)依题意可知直线AD 的斜率存在且不为0， 设直线AD 的方程为()1111y y x x =++， 代入双曲线222x y -=并化简得：()()()2222211111210x x y x x +-+-+=，①由于22112x y -=，则22112y x =-代入①并化简得：()()22211112322340x x x x x x +----=，设00(,)P x y ，则2111013423x x x x x --=+，211100112(2)342323x x x x x x x ---+=⇒=++，代入()1111y y x x =++，得10123yy x -=+，即111134,2323x y P x x ⎛⎫--- ⎪++⎝⎭，同理可得222234,2323x y Q x x ⎛⎫--- ⎪++⎝⎭，所以()()2112212121221122123232334342323y y x y x y y y x x k x x x x x x -------++==------++ ()()()212121112124377y y y y y yk x x x x -----==-⋅=--，所以217k k =是定值.5．在平面直角坐标系xOy 中，已知点(1,0)F ，点M 满足以MF 为直径的圆均与y 轴相切，记M 的轨迹为C . (1)求C 的方程；(2)设直线l 与C 交于A ，B 两点且△OAB 的面积是△FAB 面积的43倍，在x 轴上是否存在一点P 使得直线l 变动时，总有直线P A 的斜率与PB 的斜率之积为定值，若存在，求出该定值及点P 的坐标；若不能，请说明理由. 【答案】(1)24y x =(2)存在，定值1-或7-，()0,0P 【解析】 【分析】（1）设(,)M x y ，利用点M 满足以MF 为直径的圆均与y 轴相切列方程即可求解； （2）设直线AB 的方程为x ty m =+,根据△OAB 的面积是△FAB 面积的43倍，可以求出m 的值，利用韦达定理求出PA PB k k ⋅的值，由PA PB k k ⋅为定值即可判断出点P 的坐标，进而求出定值.(1)设(,)M x y ，则MF 的中点为G ,其坐标为1,22x y G +⎛⎫⎪⎝⎭，MF =G 到y 轴的距离为12x +， 则由题意可知，点M 满足以MF 为直径的圆均与y 轴相切，则|1|2x +=24y x =； (2)设直线AB 的方程为x ty m =+，由△OAB 的面积是△FAB 面积的43倍可知，点O 到直线AB 的距离是点F 到直线AB 的距离的43倍，4m =或47=m ， 可知直线AB 过点(4,0)且斜率不为0, 设()()()01122,0,,,,P x A x y B x y ，则()121221020120120PA PB y y y yk k x x x x x x x x x x =⨯=---++⋅，将直线方程与抛物线方程2,4,x ty m y x =+⎧⎨=⎩联立得2440y ty m --=， 则124y y t +=，124y y m =-，即()21212242x x t y y m t m +=++=+，()21221216y y x x m ==，故()22200442PA PB mm k t x x k m -⋅-++=，由此可知，只有当00x =时，PA PB k k ⋅才是定值， 即4PA PB k k m=-⋅， 当4m =时，1PA PB k k ⋅=-，当47=m 时，7PA PB k k =-⋅，故定点()0,0P ，定值为1-或7-. 6．已知圆1C ：()22125x y ++=，圆2C ：()2211x y -+=，动圆C 与圆1C 和圆2C 均内切.(1)求动圆圆心C 的轨迹E 的方程(2)点()1,P t （0t >）为轨迹E 上的点，过点P 作两条直线与轨迹E 交于AB 两点，直线P A ，PB 的斜率互为相反数，则直线AB 的斜率是否为定值？若是，求出定值：若不是，请说明理由.【答案】(1)22143x y +=；(2)是定值，定值为12. 【解析】 【分析】（1）利用椭圆的定义即得；（2）由题可得直线P A 的方程，联立椭圆方程可得点A 、B 横坐标，进而利用斜率公式即得.(1)由题意得()11,0C -，()21,0C .设动圆圆心C 的坐标为(),x y ，半径为r ， 则15CC r =-，21CC r =-. 从而()121244CC CC C C +=>.∴动圆圆心C 的轨迹E 是焦点为()11,0C -，()21,0C ，长轴长等于4的椭圆，且1c =，2a =. 又222a b c =+，得b =∴动圆圆心C 的轨迹E 的方程为22143x y +=.(2)由（1）可得31,2P ⎛⎫⎪⎝⎭.设直线P A 的方程为()()3102y k x k -=-≠ 则直线PB 的方程为()312y k x -=--. 设()11,A x y ，()22,B x y .由()22312143y k x x y ⎧=+-⎪⎪⎨⎪+=⎪⎩消去y ，整理得()()22223412841230k x k k x k k ++-+--=， 则212412334P k k x x k --=+，即212412334k k x k--=+.（1） 同理可得222412334k k x k +-=+.（2） ∴()()()1212121212123311222ABk x k x k x x k y y kx x x x x x ⎡⎤⎡⎤+----⎢⎥⎢⎥+--⎣⎦⎣⎦===---. 将（1）（2）代入上式，化简得12AB k =. 故直线AB 的斜率为定值12.7．已知抛物线2:2(0)C y px p =>的焦点为F ，点()04,P y 是抛物线C 上一点，点Q 是PF 的中点，且Q 到抛物线C 的淮线的距离为72． (1)求抛物线C 的方程；(2)已知圆22:(2)4M x y -+=，圆M 的一条切线l 与抛物线C 交于A ，B 两点，O 为坐标原点，求证：OA ，OB 的斜率之差的绝对值为定值． 【答案】(1)24y x =； (2)2. 【解析】 【分析】（1）根据题意即可列出等式472pp ++=，即可求出答案； （2）当直线AB 的斜率不存在时，2OA OB k k -=，当直线AB 的斜率存在时，设出直线AB 的方程为y kx b =+即点,A B 的坐标，把直线AB 与抛物线进行联立，写出韦达定理，利用到直线AB 的距离等于半径2，找到k 与b 之间的关系式，在计算OA ，OB 的斜率之差的绝对值，化简即可求出答案. (1)根据题意可列4722pp p ++=⇒= 故抛物线C 的方程为24y x =. (2)①当直线AB 的斜率不存在时，直线AB 的方程为4x =，(4,4),(4,4)A B -，1,1,2OA OB OA OB k k k k =-=-=. ②当直线AB 的斜率存在且不为0时，故设直线AB 的方程为y kx b =+， 圆M 的一条切线l 与抛物线C 交于A ，B两点，故2214b d kb ==⇒=- 设(,),(,)A A B B A x y B x y把直线AB 的方程与抛物线进行联立2222(24)04y kx bk x kb x b y x=+⎧⇒+-+=⎨=⎩ 22242,A B A B kb b x x x x k k -+=⋅=.,A B OA OB A B y y k k x x ==B A A B A B A BOA OBA B A B A Bb x x y y y x x y k k x x x x x x ---=-===22bb=====.综上所述：,OA OB的斜率之差的绝对值为定值为2.8．已知双曲线2222:1Γ-=x ya b（0a>，0b>）的左、右顶点分别为()11,0A-、()21,0A，离心率为2，过点()2,0F斜率不为0的直线l与Γ交于P、Q两点．(1)求双曲线Γ的渐近线方程；(2)记直线1A P、2A Q的斜率分别为1k、2k，求证：12kk为定值．【答案】(1)y=；(2)证明见解析.【解析】【分析】（1）由双曲线的顶点坐标、离心率，结合双曲线参数的关系求a、b，进而写出双曲线方程，即可得渐近线方程.（2）讨论l的斜率：当l k不存在求P、Q的坐标，进而可得1213kk=-；当lk存在，设()11,P x y，()22,Q x y，l为(2)y k x=-，并联立双曲线方程，应用韦达定理及斜率的两点式求证1230k k+=是否成立即可. (1)设双曲线Γ的半焦距为c，由题设，1a=，2cea==，2223b c a=-=双曲线Γ的方程为2213yx-=，故渐近线方程为y=．(2)当l的斜率不存在时，点P、Q的坐标分别为()2,3和()2,3-，所以，当11k=时有23k=-；当11k=-时有23k=，此时1213kk=-，当l的斜率k存在时，设()11,P x y，()22,Q x y，l为(2)y k x=-，将直线l代入双曲线方程得()222234430--++=k x k x k，所以212243k x x k +=-，2122433k x x k +=-，()()1212121212322331111k x k x y y k k x x x x --+=+=++-+-()()()()()()()1212123211211--++-=+-k x x x x x x ()()()()()12121212123222211--++-+-=+-k x x x x x x x x x x ()()()()12121245411-++=+-k x x x x x x因为()()()22212122443204345403+-+--++==-k k k x x x x k ，所以1230k k +=，即1213kk =-，综上，12k k 为定值，得证．。

动点与定值问题初三一、动点与定值问题解析动点与定值问题是一种常见的数学问题，主要考察学生的空间思维能力和代数运算能力。

这类问题通常涉及到几何图形中的动点和定点，通过给定的条件和关系，求出动点的轨迹或定值。

解决动点与定值问题的关键在于理解问题的几何背景和代数关系。

首先，要明确动点和定点的位置关系，以及它们之间的距离、角度等关系。

其次，要运用代数方法，将几何关系转化为代数方程或不等式，通过求解方程或不等式得到答案。

二、例题讲解例题1：在直角坐标系中，点A的坐标为(0,1)，点B的坐标为(2,0)，点C的坐标为(4,3)。

若点P是x轴上的一个动点，当△PAB的周长最小时，求点P的坐标。

分析：首先，我们可以通过平移的方式找到点P的位置。

由于点A和点B关于x轴对称，我们可以将点A关于x轴的对称点设为点P，这样△PAB的周长最小。

解：设点P的坐标为(x,0)。

由于点A和点B关于x轴对称，因此，我们有：AP = BP根据点到点的距离公式，我们可以得到：AP = √(x^2 + 1)BP = √((x-2)^2 + 1)因为AP=BP，所以：x^2 + 1 = (x-2)^2 + 1解这个方程，我们得到：x = 1所以，当△PAB的周长最小时，点P的坐标为(1,0)。

例题2：在矩形ABCD中，AB=2, BC=4, 点E是BC的中点。

将△ABE沿AE折起，使得AB=BE=2, 求二面角B-AE-D的平面角的余弦值。

分析：首先，我们需要找到二面角B-AE-D的平面角所在的三角形。

通过观察和计算，我们可以发现平面角所在的三角形是△BAE。

因此，我们需要求出△BAE 的三边长度，然后利用余弦定理求出余弦值。

解：由于AB=BE=2，AE=2√2（根据勾股定理）。

我们可以得到△BAE的三边长度分别为2、2√2、4。

根据余弦定理，我们可以得到：cos∠BAE = (AB^2 + AE^2 - BE^2) / (2 ×AB ×AE)= (4 + 8 - 4) / (2 ×2 ×2√2)= √2/2所以，二面角B-AE-D的平面角的余弦值为√2/2。

解析几何中定值与定点问题【探究问题解决的技巧、方法】(1)定点和定值问题就是在运动变化中寻找不变量的问题，基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关．在这类试题中选择消元的方向是非常关键的．(2)解圆锥曲线中的定点、定值问题也可以先研究一下特殊情况，找出定点或定值，再视具体情况进行研究．【实例探究】题型1：定值问题:例1：已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线的焦点，离心率等于（Ⅰ）求椭圆C的标准方程；（Ⅱ）过椭圆C的右焦点作直线l交椭圆C于A、B两点，交y轴于M点，若为定值.解：（I）设椭圆C的方程为，则由题意知b= 1.∴椭圆C的方程为（II）方法一：设A、B、M点的坐标分别为易知F点的坐标为（2，0）.将A点坐标代入到椭圆方程中，得去分母整理得方法二：设A、B、M点的坐标分别为又易知F点的坐标为（2，0）.显然直线l存在的斜率，设直线l的斜率为k，则直线l的方程是将直线l的方程代入到椭圆C的方程中，消去y并整理得又例2.已知椭圆C经过点A(1,3/2),两个焦点为(-1,0),(1,0).1）求椭圆方程2）E、F是椭圆上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明：直线EF的斜率为定值，并求出这个定值（1）a²-b²=c² =1设椭圆方程为x²/（b²+1）+y²/b²=1将（1，3/2）代入整理得4b^4-9b²-9=0 解得b²=3 （另一值舍）所以椭圆方程为x²/4+y²/3=1（2）设AE斜率为k则AE方程为y-(3/2)=k(x-1)①x ²/4+y ²/3=1 ②①，②联立得出两个解一个是A （1,3/2）另一个是E （x1，y1） ①代入②消去y 得（1/4+k ²/3）x ²-（2k ²/3-k ）x+k ²/3-k-1/4=0 根据韦达定理 x1·1=（k ²/3-k-1/4）/（1/4+k ²/3）③ 将③的结果代入①式得y1=（-k ²/2-k/2+3/8）/(1/4+k ²/3)设AF 斜率为-k ，F （x2，y2） 则AF 方程为y-（3/2）=-k （x-1）④ x ²/4+y ²/3=1 ② ②④联立同样解得x2=（k ²/3+k-1/4）/（1/4+k ²/3） y2=（-k ²/2+k/2+3/8）/（1/4+k ²/3） EF 斜率为（y2-y1）/(x2-x1)=1/2所以直线EF 斜率为定值，这个定值是1/2。

第十七讲平面几何中的定值问题定值问题的证明或计算，一般是通过图形的定量，如线段和定角来讨论的．如果问题中已明确给出定值，那么一般通过线段和角的和、差、倍、分的推导或计算来解决；如果问题中未给出定值，可以利用特殊的方法推测出定值，然后再加以一般化的证明．下面举几个例题，说明上述思考方法．例1 如图3－80．已知△ABC中，AB=AC，P是其底边BC上任一点，设AP交△ABC的外接圆于Q点，求证：AP·AQ为定值．分析欲证AP·AQ为定值，我们先用特殊化方法找出这个定值是什么，然后再给以一般化的证明．为此，我们取P与B(或C)重合，则Q点也必与B(或C)重合，则AP·AQ应等于AB2(定值)，以下证明这个推测．证连结BQ．因为AB=AC，所以∠ABC=∠ACB．又因为∠ACB=∠AQB，所以∠ABC=∠AQB．又因为∠BAQ=∠PAB，所以所以AP·AQ=AB2(定值)．注意如果连结QC，将怎样证明？请读者思考．例2 如图3－81．已知△ABC中，AB=AC，如果直线EF，MN都垂直于BC，试证明：不论MN，EF怎样平行移动，只要MN，EF之间的距离不变，五边形AMNFE的周长是一个定值．分析从图3－81中可以发现，如果引AD⊥BC于D，由已知条件可知AB(或AC)，AD，NF，BD(或CD)都为定值，因此，若五边形AMNFE的周长转化为以上各线段的表达式，则可判定其为定值．证作AD⊥BC于D，则所以所以又因为所以所以所以由于△ABC为确定的等腰(AB=AC)三角形，所以AD，BD，CD，AB为定值，又因为EF，MN之间距离为定长，所以NF为定值．所以五边形AMNFE的周长为定值．例3 设OA，OB是已知圆O的任意两条半径，过B引BE⊥OA于E，过E作EP⊥AB于P．求证：OP2+EP2为定值(图3－82)．分析由已知A，B为⊙O上任意两点，如果固定A，让B在圆上移动，当B点移动到半圆中点时，BE变成了半径r，E与O重合，证延长OP交⊙O于C，D(图3－82)．因为在直角三角形AEB中，∠AEB=90°，EP⊥AB于P，所以EP2=AP·PB=CP·PD＝(OC-OP)·(OD+OP)＝r2-OP2，所以EP2+OP2=r2(定值)．例4 若P为圆O内一定点，过P任作一弦AC，分别过A，C引圆的切线，再过P分别作两切线的垂线，垂足为Q，R(如图3－84)，分析根据已知，AC为过圆O内定点P的任意一弦，为了找定值，使AC特殊化，令AC为直径，则P是直径AC上的一个定点，这时由于PC，PQ同时垂直于切线，所以Q，C两点重合．同理A，R也重合(图3－85)．于是，下面证明这个推测结论．证在图3－84中，作直径AB，连BC，并过OP 作直径EF．由于∠ACB=90°，于是△ABC∽△APR．又因为△ABC∽△PCQ，所以因此例5 设d1，d2，d3是单位圆O的三条直径，且两两交角为60°，在圆周上任一点P向d1，d2，d3作垂线，垂足分别为A，B，C．证明：△ABC为定三角形(图3－86)．分析因为P为圆O上的动点，所以当P点移动到d1的一个端点D时(P与D重合，见图3-86)，因为DF⊥d3于E，而∠FOD=∠EOD=60°，所以∠于F，DE⊥d2EDF=60证连OP，作BM⊥OA于M．因为∠PAO=∠PBO=90°，所以，A，P，B，O四点共圆，且OP=1．因此，在△ABM与△OPB中，∠MAB=∠BPO，∠BMA=OBP=90°，所以△AMB∽△PBO，所以例6 相交的两圆的交点为A，B，经过B点所作的任意直线与两圆的交点分别是C，D，那么AC∶AD是定值(图3－87)．分析因CD是过B点的任意直线，为确定AC∶AD，使CD特殊化，令其垂直于AB，这时因为∠ABC=∠CAD=90°，那么AC，AD必定是两圆直径．若设d，1d2为两圆直径，则AC∶AD=d1∶d2(定值)．下面对以上推测做一般性证明．证在图3－88中，设CD是过B点交两圆于C，D 的任一直线，过B作C′D′交两圆于C′，D′，且使AB⊥C′D′于B，连AD′，D′D，AC′，CC′，易知∠ADD′=∠ACC′=90°．又∠AD′D=∠ABD=∠AC′C，所以△ADD′∽△ACC′，所以AC∶AD=AC′∶AD′=d1∶d2(定值)．练习十七1．如图3－89．直线l1∥l2∥l3，A，B是l2上两定点，P，Q分别为l1和l3上的动点．求证：四边形PAQB的面积为定值．2．如图3－90．△ABC是正三角形，由其中任一点P，向三边引垂线，设垂足分别为M，N，Q，求证：PM+PN+PQ为定值．3．已知正方形ABCD，以A为圆心，AB为半径在正方形内作圆别交BC，CD于E，F．求证：∠EAF为定值．4．若M，N为△ABC的边AB，AC的中点，P为MN上的任意5．两平行线l1，l2分别与已知圆O相切于A，B，作圆O的任意切线l3与l1，l2分别交于C，D．求证：AC·BD为定值．。

平面几何中的定值问题开场白：同学们，动态几何类问题是近几年中考命题的热点，题目灵活、多变，能够全面考查同学们的综合分析和解决问题的能力。

这类问题中就有一类是定值问题，下面我们来看几道题：【问题1】已知一等腰直角三角形的两直角边AB=AC=1，P 是斜边BC 上的一动点，过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则PE+PF= 。

方法1：特殊值法：把P 点放在特殊的B 点或C 点或BC 中点。

此种方法只适合小题。

方法2：等量转化法：这是绝大部分同学能够想到的方法，PF=AE,PE=BE,所以PE+PF=BE+AE 。

方法3：等面积法：连接AP ，ABC ABP APC S S S AB AC AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅AB PE PF ⇒=+总结语：这虽然是一道动态几何问题，难吗？不难，在解决过程中（方法2抓住了边长AB的不变性和PE,PF 与BE,AE 的不变关系；方法3抓住了面积的不变性），使得问题迎刃而解。

设计：大部分学生都能想到方法2，若其他两种方法学生没有想到，也不要深究，更不要自己讲掉。

此题可叫差生或中等偏下的学生回答（赛比艳，艾科）（设计意图：由简到难，让程度最差的同学也有在课堂上展示自我的机会。

）过渡：这道题太简单了，因为等腰直角三角形太特殊了，我若把等腰直角三角形换成一般的等腰三角形，问题有没有变化，又该如何解决？请看：【变式1】若把问题1中的等腰直角三角形改为 等腰三角形，且两腰AB=AC=5，底边BC=6， 过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则PE+PF 还是定值吗？若是，是多少？若不是，为什么?方法1：三角形相似进行量的转化ABM PBE PCF∆∆∆,AM PE PF AM PB AM PCPE PF AB PB PC AB AB⋅⋅⇒==⇒==()462455AM PB PC AM BC PE PF AB AB +⋅⋅⇒+====（板书） （M 为BC 中点）（解题要点：等腰三角形中，底边上的中线是常作的辅助线，抓住这条线的长度是不变量这个特点，建立PE,PF 与AM 之间的联系，化动为静）方法2：等面积法：ABC ABP APC S S S BC AM AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅642455BC AM PE PF AB ⋅⋅⇒+===（M 为BC 中点） （板书）（解题要点：抓住三角形面积是个不变量，用等面积法求解，这是在三角形中求解与垂线段有关的量的常用方法。

平面几何的定值平面几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题.•所谓几何定值问题就是要求出这个定值.在解决这类问题的过程中,可以直接通过计算来求出定值;也可以先考虑某一个特殊情形下的该相关值,然后证明当相应几何元素变化时,此值保持不变.例1 已知△ABC 内接于⊙O,D 是BC•或其延长线上一点,AE 是△ABC 外接圆的一条弦,若∠BAE=∠CAD.求证:AD.AE 为定值.证明 如图 (1),当点D 是BC 上任意一点且∠BAE=∠CAD 时,连结BE, 则∠E=∠C,∠BAE=∠CAD, ∴△ABE ∽△ADC. ∴AB AEAD AC=,即AD ·AE=AB ·AC 为定值. 如图 (2),当点D 在BC 的延长线上时,∠BAE=∠CAD.此时,∠ACD=∠AEB. ∴△AEB ∽△ACD,∴AB AEAD AC= 即AD ·AE=AB ·AC 为定值.综上所述,当点D 在BC 边上或其延长线上时,只要∠CAD=∠BAE,总有AD ·AE 为定值.先探求定值,当AD ⊥BC,AE 为圆的直径时,满足∠BAE=∠CAD 这一条件,•不难发现△ACD ∽△AEB,所以AD ·AE=AB ·AC,因为已知AB,AC 均为定值.•再就一般情况分点D•在BC 上,点D 在BC 的延长线上两种情况分别证明.练习1.已知MN 是⊙O 的切线,AB 是⊙O 的直径.求证:点A 、B 与MN 的距离的和为定值. (答案)定长为圆的直径;2.已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T.求证:PC:PT是定值.2.利用特殊位置探求定值(当PC构成直径时)(R,r是两圆的半径).3.⊙O1与⊙O2相交于P、Q两点,过P作任一直线交⊙O1于点E,交⊙O2于点F.求证:∠EQF为定值.因∠E,∠F为定角(大小固定)易得∠EQF为定值.26．如图16，在平面直角坐标系中，直线y=x轴交于点A，与y轴交于点C，抛物线2(0)y ax x c a=+≠经过A,B,C三点．（1）求过A,B,C三点抛物线的解析式并求出顶点F的坐标；（2）在抛物线上是否存在点P，使⊿ABC为直角三角形，若存在，直接写出P点坐标；若不存在，请说明理由；（3）试探究在直线AC上是否存在一点，使得⊿BMF的周长最小，若存在，求出M点的坐标；若不存在，请说明理由．26．解：（1）直线y=x轴交于点(10)A∴-，，(0C·························1分 点A C，都在抛物线上，0a cc⎧=++⎪∴⎨⎪=⎩ac⎧=⎪∴⎨⎪=⎩x∴抛物线的解析式为233y x x =-················ 3分 ∴顶点13F ⎛⎫- ⎪ ⎪⎝⎭， ··························· 4分 （2）存在 ································ 5分1(0P ······························· 7分2(2P ······························· 9分 （3）存在 ································ 10分理由： 解法一：延长BC 到点B '，使B C BC '=，连接B F '交直线AC 于点M ，则点M 就是所求的点． ························· 11分 过点B '作B H AB '⊥于点H ．B点在抛物线2y x =-上，(30)B ∴，在Rt BOC △中，tan 3OBC ∠=，30OBC ∴∠=，BC =在Rt BB H '△中，12B H BB ''==6BH H '==，3OH ∴=，(3B '∴--， ·············· 12分设直线B F '的解析式为y kx b =+3k b k b ⎧-=-+⎪∴⎨=+⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y x ∴=···························· 13分xy x ⎪∴⎨=⎪⎩解得7y ⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时37M ⎛ ⎝⎭，． ·· 14分 解法二：过点F 作AC 的垂线交y 轴于点H ，则点H 为点F 关于直线AC 的对称点．连接BH 交AC 于点M ，则点M 即为所求． ········· 11分过点F 作FG y ⊥轴于点G ，则OB FG ∥，BC FH ∥．90BOC FGH ∴∠=∠= ，BCO FHG ∠=∠ HFG CBO ∴∠=∠同方法一可求得(30)B ，． 在Rt BOC △中，tan OBC ∠=，30OBC ∴∠=，可求得GH GC ==， GF ∴为线段CH 的垂直平分线，可证得CFH △为等边三角形，AC ∴垂直平分FH ．即点H 为点F 关于AC的对称点．0H ⎛∴- ⎝⎭，·············· 12分 设直线BH 的解析式为y kx b =+，由题意得03k b b =+⎧⎪⎨=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y ∴=···························· 13分xy y =-⎪∴⎨⎪=⎩解得7y ⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时37M ⎛ ⎝⎭，． ·· 14分。

专题:解析几何中五类定点定值问题的研究与拓展【问题提出】1.无论k 取任何实数，直线(1 +4k)x-(2 -3k)y+(2 -14k) =0必经过一个定点，则这个定点的坐标为2.已知直线丨：2ax +by-a +b =0 ；圆C : x 2 + y 2 - 2x-1 = 0 ,则直线I 与圆C 的位置关系为=1(a >■ b A 0)，点A,F 分别是椭圆C 的左顶点和左焦点，点P 是圆PA 若 ——为常数，则椭圆的离心率为PF过点(1, 0).若对任意的实数 m ,定直线 l 被圆C 截得的弦长为定值，则直线 I 的方程为.2x + y — 2= 0【探究拓展】2探究1：已知F 1、F 2分别为椭圆 G ：詁+詁=1(a Ab 》。

)的上、下焦点，其中F 1也是抛物线C 2：x 2=4y 的5焦点，点M是C 1与C 2在第二象限的交点，且阿七.(1) 求椭圆C 1的方程.(2)已知点P(1,3)和圆O ：X 2 +y 2 =b 2,过点P 的动直线I 与圆0相交于不同的两点 A,B ,在线段AB 上取一 点Q ,满足：AP = -A P B ,瓷=Z QB ,( A H 0且A H ±1).求证：点Q 总在某定直线上.4.平面直角坐标系 xOy 中,已知圆C ： x 2+ y 2— (6 — 2m)x — 4my + 5m 2— 6m = 0,直线 I 经 2 2x y3.已知椭圆C : —2 + —2a b2 2 2 O : x + y =b 上的动点,1 4变式1 :在平面直角坐标系 xOy 中，已知定点A( — 4,0)、B(4,0),动点P 与A 、B 两点连线的斜率之积为①求O M 的方程;直线AF i , AF 2分别交椭圆于点 (1 )求证直线BO 平分线段AC ;(2) 设点P (m , n ) ( m , n 为常数)在直线BO 上且在椭圆外，过P 的动直线(1)求点 p 的轨迹方程;(2)设点 P 的轨迹与y 轴负半轴交于点 C.半径为r 的圆M 的圆心M 在线段 AC 的垂直平分线上，且在 y轴右侧，圆 M 被y 轴截得的弦长为a②当r 变化时，是否存在定直线 I 与动圆M 均相切？如果存在，求出定直线I 的方程；如果不存在，说明理由.2 2X y 变式2 :已知椭圆E : —2 + a b= 1(a Ab >0)的离心率为 弓3 ,它的上顶点为A ,左、右焦点分别为F 1,F 2 ,MP N ,在线段MN 上取点Q ,满足—PN=器，试证明点Q 恒在一定直线上.B ,C .I 与椭圆交于两个不同点 M ,P探究2:平面直角坐标系xoy 中，圆G：(x + 3)2+(y -1)2=4和圆C2：(X-4)2+(y-5)2=4.(1)若直线I过点A(4,0)，且被圆C I截得的弦长为2J3，求直线I的方程;(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线|1和|2，它们分别与圆C1和圆C2相交，且直线|1被圆C1截得的弦长与直线12被圆C2截得的弦长相等，试求所有满足条件的点P的坐标.-- ----------- ►A H变式1：在直角坐标系xOy中，点M到点F i(-J3,0)，F2(J3,O)的距离之和为4，点M的轨迹是C，与x轴的负半轴交于点A，轨迹C上有不同的两点P和Q，且AP-AQ-O(1)求轨迹C的方程;(2)直线PQ是否过x轴上的一定点，若过定点，请给出证明，并求出该定点？若不过定点，请说明理由.变式2:已知圆C:x2+y2=9，点A(—5,0)，直线l :x-2y = 0.(1)求与圆C相切，且与直线I垂直的直线方程;PB (2)在直线OA上(O为坐标原点)，存在定点B (不同于点A),满足：对于圆C上任一点P ,都有——PA 为一常数，试求所有满足条件的点B的坐标.变式3 :在平面直角坐标系xOy中，已知直线1: 2岳—y+ 3+ 8返=0和圆C1: x2+ y2+ 8x + F= 0.若直线I被圆C i截得的弦长为2j3 .设圆C i和x轴相交于A, B两点，点P为圆C i上不同于A, B的任意一点，直线FA, PB交y轴于M, N两点.当点P变化时，以MN为直径的圆C?是否经过圆C1内一定点?请证明你的结论;变式4:如图，椭圆的中心为原点 O ,离心率e =¥，—条准线的方程为x = 2{2.(1)求该椭圆的标准方程; (2)设动点P 满足：O P = OM + 2ON ，其中M , N 是椭圆上的点，直线 0M 与ON 的斜率之积为一2,问: 是否存在两个定点 F i , F 2，使得|PFJ +|PF 2I 为定值？若存在，求出 F i , F 2的坐标；若不存在，说明理由.5:已知左焦点为F(— 1 , 0)的椭圆过点E(1 , 亜).过点P(1 , 1)分别作斜率为k i , k 2的椭圆的动弦 3 CD ，设M , N 分别为线段AB , CD 的中点. 求椭圆的标准方程； 若P 为线段AB 的中点，求k i ；若k i + k 2=1，求证直线MN 恒过定点，并求出定点坐标.变式 AB ,2 2 X y探究 3 :已知椭圆p +笃=1（a；＞bA0）的左顶点为a b+ y2+ J3x -3y -6 = 0过A, F2两点求椭圆标准的方程; A，左、右焦点分别为F1,F2，且圆X2(2) 设直线PF2的倾斜角为a,直线PF1的倾斜角为3,当a,3- a= I n时证明：点P在一定圆上;3变式设椭圆的上顶点为Q,在满足条件（2）的情形下证明: PQ = PF i + PF2 .1:在平面直角坐标系xOy中，圆C的方程为（X—1）2+ y2= 4, P为圆C上一点•若存在一个定圆过P作圆M的两条切线PA, PB,切点分别为A, B，当P在圆C上运动时，使得/ APB恒为60。

九年级数学平面几何中的定值问题例题讲解知识点，重点，难点所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内变化时，与它有关的某种几何量却始终保持不变（或几何元素间的某种几何性质或位置关系不变）。

平面几何定值一般可分为两类：一类是定量问题（如定长度、定角、定比、平方和或倒数和为定值等）；一类是定形问题（如定点、定线、定圆或弧、定方向等），它们有共同的基本特点，即给定条件中一般由固定条件和变动条件两部分组成。

一般来说，求解定值问题的方法有：图形分析法。

画出符合条件的图形后，分析图中几何元素的数量关系及位置关系，直接寻求出定值并证明。

特殊位置法。

不论图形如何变动，定值这一共性始终不变，因此可选择图形的特殊位置（如极限位置、临界位置）加以探求。

参数计算法。

图形运动中，选取其中的变量（如线段长、角度、面积等）作为参数，将要求的定值用参数表出，然后消去参数即得定值。

例题精讲例1：如图，已知⊙O 及弦AB ，P 为⊙O 上任一点，PA 、PB 分别交AB 中垂线于E 、F ，求证：OE ·OF 为定值。

分析 若在⊙O 上的点P 运动到特殊位置点Q ，则点E ，点F 都和Q 点重合，于是得到OE ·OF =OQ 2，由此可推想，该定值可能为⊙O 半径的平方。

证明 因为OE 是弦AB 的中垂线，所以 AQ BQ=，所以∠AOE=∠BOE ， 所以 1.2mAOE AB ∠=又因为 1,2m PAB BP ∠= 1,2m PBA AP ∠=∠EPB =∠PAB ＋∠ABP ，所以∠AOE = ∠EPB ，所以A 、O 、F 、P 四点共圆，所以∠OFB =∠OAE .又因为∠FOB =∠AOE ，所以△FOB ∽△OAE ，所以,OF OB OA OE =即OE ·OF ＝OA ·OB .因为OA =OB ，所以OE ·OF =OA 2（定值）。

第二十三讲平面几何的定值与最值问题【趣题引路】传说从前有一个虔诚的信徒,他是集市上的一个小贩.••每天他都要从家所在的点A出发,到集市点B,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O,•而周围上的点都是供信徒朝拜的顶礼地点如图1.这个信徒想,我怎样选择朝拜点,才能使从家到朝拜点,•然后再到集市的路程最短呢?(1) (2)解析在圆周上选一点P,过P作⊙O的切线MN,使得∠APK=∠BPK,即α=β.那么朝圣者沿A→P→B的路线去走,距离最短.证明如图2,在圆周上除P点外再任选一点P′.连结BP•′与切线MN•交于R,AR+BR>AP+BP.∵RP′+AP′>AR.∴AP′+BP′=AP′+RP′+RB>AR+BP>AP+BP.不过,用尺规作图法求点P的位置至今没有解决.•“古堡朝圣问题”属于数学上“最短路线问题”,解决它的方法是采用“等角原理”.【知识延伸】平面几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题.•所谓几何定值问题就是要求出这个定值.在解决这类问题的过程中,可以直接通过计算来求出定值;也可以先考虑某一个特殊情形下的该相关值,然后证明当相应几何元素变化时,此值保持不变.例1如果△ABC的外接圆半径R一定,求证: abcS是定值.(S表示△ABC的面积)解析由三角形面积S=12absinC和正弦定理sincC=2R,∴c=2RsinC.∴abcS=2sincC=4sinsinR CC=4R是定值.点评通过正弦定理和三角形面积公式经过变形,计算出结果是4R,即为定值.平面几何中不仅有等量关系,还有不等关系,例如在变动一些几何元素时,•某一相关的值保持不大于(或不小于)某个定值,如果这个定值在某个情形下可以取得,•这就是一个几何极值.确定几何极值的问题称为几何极值问题,解决这些问题总要证明相关的几何不等式,并指明不等式成为等式的情形(或者至少证明不等式可以成为等式).例2 如图,已知⊙O的半径R=33,A为⊙O上一点,过A作一半径为r=3的⊙O′,问OO′何时最长?最长值是多少?OO′何时最短?最短值是多少?解析当O′落在OA的连线段上(即⊙A与线段OA的交点B时)OO′最短,且最短长度为33-3 ;当O′落在OA的延长线上(即⊙O与OA的延长线交点C时)OO′最长,且最长的长度为33+3 .点评⊙O′是一个动圆,满足条件的⊙O′有无数个,但由于⊙O′过A点,所以⊙O′的圆心O′在以A为圆心半径为3的⊙A上.【好题妙解】佳题新题品味例1 如图,已知P为定角O的角平分线上的定点,过O、P•两点任作一圆与角的两边分别交于A、B两点.求证:OA+OB是定值.证明连结AP、BP,由于它们为有相同圆周角的弦,AP=PB,不妨记为r.•另记x1=OA,x2=OB.对△POA应用余弦定理,得x12+OP2-2OP·cos∠AOP·x1=r2.故x1为方程x2-2OP·cos 12∠AOB·x+(O P2-r2)=0的根,同理x2亦为其根.因此x1,x2为此方程的两根,由韦达定理,得x1+x2=2OP(12∠AOB)是定值.点评当x 1=x 2时,x 1+x 2为此定值,事实上此时OP 一定是直径.例2 如图,在矩形ABCD 中,AB=8,BC=9,⊙O 与外切,且⊙O 与AB 、BC•相切.⊙O ′与AD 、CD 相切,设⊙O 的半径为x,⊙O 与⊙O ′的面积的和为S,求S•的最大值和最小值. 解析 设⊙O ′的半径为y,过O 与O ′分别作CD 与BC 的垂线OH,O ′F,•垂足分别为H,F,OH 、O ′F 交于点E,则有:O ′E=8-(x+y),OE=9-(x+y) 由勾股定理可得:(x+y)2=[8-(x+y)]2+[9-(x+y)]2. 整理,得(x+y-29)(x+y-5)=0,由题意知1≤x ≤4,∴x+y=5,y=-x+5,∴S=πx+πy=π(2x-10x+25),=2π[(x-52)2+254], 故当x=52时,S min =252π; 当x=4时,S=17π.点评先由已知求出⊙O ′的半径也⊙O 的半径x 之间的关系,然后再根据面积公式写出S 与x 之间的关系,这个关系就是一个函数关系,再通过函数的性质得解.中考真题欣赏例 (南京市中考题)如图,⊙O 1与⊙O 2内切于点P,又⊙O 1切⊙O 2•的直径BE 于点C,连结PC 并延长交⊙O 2于点A,设⊙O 1,⊙O 2的半径分别为r 、R,且R ≥2r.•求证:PC ·AC 是定值.解析 若放大⊙O 1,使⊙O 1切⊙O 2的直径于点O 2(如图), 显然此时有PC ·AC=PO 2·AO 2=2r ·R(定值). 再证明如图的情况:连结C O 1,PO 2,• 则PO 2•必过点O 1,•且O 1C ⊥BE,得CO 2=22121O O O C -=22R Rr -,从而BC=R+22R Rr -,EC=R-22R Rr -.所以PC ·AC=EC ·BC=2Rr,故PC ·AC 是定值. 点评解答几何定值问题时,可先在符合题目条件的前提下用运动的观点,从特殊位置入手,找出相应定值,然后可借助特殊位置为桥梁,完成一般情况的证明.竞赛样题展示例1 (第十五届江苏省初中数学竞赛题)如图,正方形ABCD的边长为1,•点P为边BC 上任意一点(可与点B或点C重合),分别过点B、C、D作射线AP的垂线,•垂足分别为点B′、C′、D′.求BB′+CC′+DD′的最大值和最小值.解析∵S△DPC= S△APC =12 AP·CC′,得S 四边形BCDA= S△ABP+ S△ADP+ S△DPC= 12AP(BB′+DD′+CC′),于是BB′+CC′+DD′=2 AP.又1≤AP≤2,故2≤BB′+CC′+DD•′≤2,∴BB′+CC′+DD′的最小值为2,最大值为2.点评本题涉及垂线可考虑用面积法来求.例2 (2000年“新世纪杯”广西竞赛题)已知△ABC内接于⊙O,D是BC•或其延长线上一点,AE是△ABC外接圆的一条弦,若∠BAE=∠CAD.求证:AD.AE为定值.证明如图 (1),当点D是BC上任意一点且∠BAE=∠CAD时,连结BE,则∠E=∠C,∠BAE=∠CAD,∴△ABE∽△ADC.∴AB AEAD AC=,即AD·AE=AB·AC为定值.如图 (2),当点D在BC的延长线上时,∠BAE=∠CAD.此时,∠ACD=∠AEB.∴△AEB∽△ACD,∴AB AE AD AC=即AD·AE=AB·AC为定值.综上所述,当点D在BC边上或其延长线上时,只要∠CAD=∠BAE,总有AD·AE为定值. 点评先探求定值,当AD⊥BC,AE为圆的直径时,满足∠BAE=∠CAD这一条件,•不难发现△ACD ∽△AEB,所以AD·AE=AB·AC,因为已知AB,AC均为定值.•再就一般情况分点D•在BC上,点D在BC的延长线上两种情况分别证明.全能训练A级1.已知MN是⊙O的切线,AB是⊙O的直径.求证:点A、B与MN的距离的和为定值.2.已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T.求证:PC:PT是定值.3.⊙O 1与⊙O 2相交于P 、Q 两点,过P 作任一直线交⊙O 1于点E,交⊙O 2于点F.求证:∠EQF 为定值.4.以O 为圆心,1为半径的圆内有一定点A,过A 引互相垂直的弦PQ,RS.求PQ+RS 的最大值和最小值.5.如图,已知△ABC 的周长为2p,在AB 、AC 上分别取点M 和N,使MN•∥BC,•且MN 与△ABC 的内切圆相切.求:MN 的最值.CABMNA 级(答案)1.定长为圆的直径;2.利用特殊位置探求定值(当PC 构成直径时)是两圆的半径). 3.因∠E,∠F 为定角(大小固定)易得∠EQF 为定值.4.如图,设OA=a(定值),过O 作OB ⊥PQ,OC ⊥RS,B 、C 为垂足, 设OB=x,OC=y,0≤x ≤a,(0≤y ≤a),且x 2+y 2=a 2. 所以所以∴(PQ+RS)2=4(2-a 2+而x 2y 2=x 2(a 2-x 2)=-(x 2-22a )2+44a . 当x 2=22a 时,(x 2y 2)最大值=44a .此时;当x 2=0或x 2=a 2时,(x 2y 2)最小值=0,此时(PQ+RS )最小值=2（）. 5.设BC=a,BC 边上的高为h,内切圆半径为r. ∵△AMN ∽△ABC,2MN h r BC h -=,MN=a(1-2rh),• 由S △ABC =rp,∴r=2ABC S ahp p∆=, ∴MN=a(1-a p )=p ·a p (1-a p )≤p 2(1)2aa p p⎡⎤+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=4p ,当且仅当a p =1-a p ,即a=2p 时,取等号,∴MN 的最大值为4p.B级1.如图1,已知正方形ABCD的边长为3,点E在BC上,且BE=2,点P在BD上,则PE+PC的最小值为( )A.23B. 13C. 14D.15E D CAB PSQA B PM(1) (2) (3)2.用四条线段a=14,b=13,c=9,d=7.作为四条边构成一个梯形,•则在所构成的梯形中,中位线长的最大值是__________.3.如图2,⊙O的半径为2,A、B两点在⊙O上,切线AQ和BQ相交于Q,P是AB•延长线上任一点,QS⊥OP于S,则OP·OS=_______.4.已知,如图3,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE•、•MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( •)A.定直线B.经过定点C.一定不过定点D.以上都有可能5.如图,已知⊙O的半径为R,以⊙O上一点A为圆心,以r为半径作⊙A,•又PQ与⊙A 相切,切点为D,且交⊙O于P、Q.求证:AP·AQ为定值.6.如图,⊙O 1与⊙O 2相交于A 、B 两点,经过点B•的一直线和两圆分别相交于点C 和D,设此两圆的半径为R 1,R 2.求证:AC:AD=R 1:R 2.B 级(答案)1.B.∵A 、C 关于BD 对称,连结AE 交BD 于P,此时PE+PC=AE 最短.2.11.5 (1)当上底为7,下底分别为14,13,9时,中位线长分别为10.5,10,8; (2)当上底为9和13时,均构不成梯形.3.连结OQ 交AB 于M,则OQ ⊥AB.连结OA,则OA ⊥AQ. ∵∠QMP=∠QSP=90°,∴S,P,•Q,M 四点共圆,故OS ·OP=OM ·OQ. 又∵OM ·OQ=OA 2=2,∴OS ·OP=2.4.B.由图可知直线MN 可看作⊙O 和⊙O ′的割线, 当M 在点A 时,直线MN 变为⊙O•′的切线, 当M 在点B 时,直线MN 变为⊙O 的切线.这两种情况是以AB•为直角边的等腰直角三角形的两直角边所在的直线,交点是第三个顶点M.M 是AB 的中点时,MN 是AB•的垂直平分线,也过第三个顶点,所以选B. 5.如图,作⊙O 的直径AB,连结AD. ∵PQ 切⊙A 于D,∴AD ⊥PQ, ∴AP ·AQ=AD ·AB.•而AD=r,AB=2R,∴AP ·AQ=2Rr 为定值.6.作AN ⊥CD,垂足为点N,连结AB,有AC.AB=AN.2R1,① AB ·AD=AN ·2R 2 .② ①÷②,得12R AC AD R ,∴AC:A D=R 1:R 2.。

解析几何中的定值定点问题(一)与直线x -y 2=0相切. ⑴求椭圆C 的方程；⑵设P(4, 0) , M 、N 是椭圆C 上关于x 轴对称的任意两个不同的点，连结 PN 交椭圆C 于另一点E ，求直线PN 的斜率的取值范围；⑶在⑵的条件下，证明直线 ME 与x 轴相交于定点. 解：⑴由题意知e =£3，所以e 2 =与=a ;b=3，即玄2 =4b 2，又因为b ! 1,所以a 2a a 4J l +1222X2a =4,b =1，故椭圆C 的方程为C : - y =1 .4⑵由题意知直线 PN 的斜率存在，设直线 PN 的方程为y =k(x _4)①+y 二k(x 一4)联立 X 2 2 消去 y 得：(4k 2 -1)x 2 -32k 2x 4(16k 2-1) =0 ,4 y T由,;=(32k 2)2 _4(4k 2 1)(64k 2 —4) 0 得 12k 2 -1 ：：:0,又k =0不合题意，所以直线PN 的斜率的取值范围是3::: k ：:：0或0 :：: k 3 .6 6⑶设点 N(N ,yj E(X 2, y 2)，则 M (为，-yj ，直线 ME 的方程为 y-y ?二 一(x-x ?),X 2 —X 1令 y=0，得 x=X 2——X^) , 将 射=k(X 1 - 4), y 2 = k(X 2 - 4)代入整理，得 x = _4(XX 2). ②y 2 +y 1X 1 +血 一82 2由得①X 1 X 2二卫!J, X 1X 2二竺 4代入②整理，得X=1 ,4k -+1 4k +1 所以直线ME 与x 轴相交于定点(1, 0).【针对性练习1]在直角坐标系xOy 中，点M 到点F 1 i 、3,0 , F 2 .3,0的距离之和是4，点M 的轨 迹是C 与x 轴的负半轴交于点 A ，不过点A 的直线l : ^ kx b 与轨迹C 交于不同的两点 P 和Q . ⑴求轨迹C 的方程；⑵当AP AQ =0时，求k 与b 的关系，并证明直线l 过定点.解：⑴•••点M 到.[73,0 , . 3 ,0的距离之和是4 , ••• M 的轨迹C 是长轴为4 ,焦点在x 轴上焦中为2 32的椭圆，其方程为-y 2 =1 .、定点问题【例1 ].已知椭圆C : 2 2孚 Z =1(a b 0)的离心率为a b仝，以原点为圆心，椭圆的短半轴长为半径的圆 2AO J7—⑵将y=kx・b，代入曲线C的方程，整理得(1 4k2)x28 2kx ^0，因为直线|与曲线C交于不同的两点P 和Q，所以厶=64kb -4(1 4k )(4b — 4) =16(4k -b 1) 0 ①设P X i , y i ，Q| x2 , y2 ，则X i :' X? 2 ，X i X? 2 ②f' 1+4k 1+4k且y i y^(kX i b)(kX? ■ b^(k2X i X?) kb(X i X?)b2，显然，曲线C与X轴的负半轴交于点 A -2 , 0，所AP = X 2 , y ，AQ = X? 2 , y?.由AP AQ = 0，得(x「2)(x? 2) y y? = 0 .将②、③代入上式，整理得12k? -16kb • 5b? =0.所以(2k -b) (6k -5b) = 0 ,即b = 2k或b .经检验,5都符合条件①，当b=2k时，直线I的方程为y =kx・2k •显然，此时直线I经过定点-2 , 0点•即直线|b =6k时，直线I的方程为y = kx ■ 6k =k经过点A，与题意不符.当5 5b = @ k，且直线I经过定点5【针对性练习2】在平面直角坐标系xoy中，如图，已知椭圆? ?—-匚=1的左、右顶点为A、B，右焦点9 5为F。

解析几何中的定点定值问题考纲解读：定点定值问题是解析几何解答题的考查重点。

此类问题定中有动，动中有定，并且常与轨迹问题，曲线系问题等相结合，深入考查直线的圆，圆锥曲线，直线和圆锥曲线位置关系等相关知识。

考查数形结合，分类讨论，化归与转化，函数和方程等数学思想方法。

一、定点问题解题的关健在于寻找题中用来联系已知量，未知量的垂直关系、中点关系、方程、不等式，然后将已知量，未知量代入上述关系，通过整理，变形转化为过定点的直线系、曲线系来解决。

例1、已知A 、B 是抛物线y 2=2p x (p >0)上异于原点O 的两个不同点，直线OA 和OB 的倾斜角分别为α和β，当α、β变化且α+β=4π时，证明直线AB 恒过定点，并求出该定点的坐标。

解析： 设A 〔121,2y p y 〕，B 〔222,2y py 〕，则 212tan ,2tan y py p==βα，代入1)tan(=+βα得221214)(2p y y y y p -=+ 〔1〕 又设直线AB 的方程为b kx y +=，则022222=+-⇒⎩⎨⎧=+=pb py ky pxy bkx y ∴kpy y kpby y 2,22121=+=，代入〔1〕式得pk p b 22+= ∴直线AB 的方程为)2(2p x k p y +=- ∴直线AB 过定点〔-)2,2p p说明：此题在特殊条件下很难探索出定点，因此要从已知出发，把所求的定点问题转化为求直线AB ，再从AB 直线系中看出定点。

例2．已知椭圆C ：22221(0)x y a b a b+=>>，以原点为圆心，椭圆的短半轴长为半径的圆与直线0x y -相切． ⑴求椭圆C 的方程；⑵设(4,0)P ，M 、N 是椭圆C 上关于x 轴对称的任意两个不同的点，连结PN 交椭圆C 于另一点E ，求直线PN 的斜率的取值范围；⑶在⑵的条件下，证明直线ME 与x 轴相交于定点．解析：⑴由题意知c e a ==22222234c a b e a a -===，即224a b =，又因为1b ==，所以224,1a b ==，故椭圆C 的方程为C ：2214x y +=．⑵由题意知直线PN 的斜率存在，设直线PN 的方程为(4)y k x =- ① 联立22(4)14y k x x y =-⎧⎪⎨+=⎪⎩消去y 得：2222(41)324(161)0k x k x k --+-=， 由2222(32)4(41)(644)0k k k ∆=-+->得21210k -<， 又0k =不合题意，所以直线PN的斜率的取值范围是0k <<或0k <<． ⑶设点1122(,),(,)N x y E x y ，则11(,)M x y -，直线ME 的方程为212221()y y y y x x x x +-=--， 令0y =，得221221()y x x x x y y -=-+，将1122(4),(4)y k x y k x =-=-代入整理，得12121224()8x x x x x x x -+=+-． ②由得①2212122232644,4141k k x x x x k k -+==++代入②整理，得1x =， 所以直线ME 与x 轴相交于定点(1,0)．【针对性练习1】 在直角坐标系xOy 中，点M到点()1,0F，)2,0F 的距离之和是4，点M 的轨迹是C 与x 轴的负半轴交于点A ，不过点A 的直线:l y kx b =+与轨迹C 交于不同的两点P 和Q ． ⑴求轨迹C 的方程；⑵当0AP AQ ⋅=时，求k 与b 的关系，并证明直线l 过定点．解：⑴∵点M到(),0，),0的距离之和是4，∴M 的轨迹C 是长轴为4，焦点在x轴上焦中为的椭圆，其方程为2214x y +=．⑵将y kx b =+，代入曲线C的方程，整理得22(14)40k x +++= ，因为直线l 与曲线C 交于不同的两点P 和Q ，所以222222644(14)(44)16(41)0k b k b k b ∆=-+-=-+> ① 设()11,P x y ，()22,Q x y，则12x x +=，122414x x k=+ ②且2212121212()()()()y y kx b kx b k x x kb x x b ⋅=++=+++，显然，曲线C 与x 轴的负半轴交于点()2,0A -，所以()112,AP x y =+，()222,AQ x y =+．由0AP AQ ⋅=，得1212(2)(2)0x x y y +++=．将②、③代入上式，整理得22121650k kb b -+=．所以(2)(65)0k b k b -⋅-=，即2b k =或65b k =．经检验，都符合条件①，当2b k =时，直线l 的方程为2y kx k =+．显然，此时直线l 经过定点()2,0-点．即直线l 经过点A ，与题意不符．当65b k =时，直线l 的方程为6556y kx k k x ⎛⎫=+=+ ⎪⎝⎭．显然，此时直线l 经过定点6,05⎛⎫- ⎪⎝⎭点，且不过点A ．综上，k 与b 的关系是：65b k =，且直线l 经过定点6,05⎛⎫- ⎪⎝⎭点． 【针对性练习2】在平面直角坐标系xoy 中，如图，已知椭圆15922=+y x 的左、右顶点为A 、B ，右焦点为F 。

解析几何中的定值问题定值问题是解析几何常见题型，是备受关注的焦点之一，它体现了动与静的完美统一，其内容丰富，综合性较强，因而趣味性也较强。

下举例谈谈这类问题的常见类型及求解策略。

一、弦长比值型 例 1：双曲线222222b a y a x b =-的离心率为 e （e>0），PQ 为过焦点 F 而不垂直于 F 所在的对称轴的弦，且 PQ 的中垂线交 x 轴于 R ，求证：||||FR PQ 为定值。

证明:设F （－c ，0）为双曲线方程的一个焦点，弦 PQ 过 F 且中点为 M ，设 P ，Q 两点坐标分别为),(),,(2211y x y x PQ 所在直线方程为 y=k(x+c)。

联立方程222222ba ya xb =-及y=k(x+c)消去y 得:⎪⎪⎩⎪⎪⎨⎧---=-=+⇒=----222222222122222212222222222222022)(k a b b a c k a x x k a b ck a x x ba c k a cx k a x k ab ,从而弦PQ 的中点M 的坐标为),(222222222ka b kc b ka b c k a --,直线MR 的方程为:222322222222220)(1ka b ck x ，y ka b c k a x kka b kc b y R -==---=--得，令。

故||)1(2||1||,||)1(||||222222122222222232ka b k ak x x kPQ k a b k c k c ka b ck FR -+=-+=-+=+-=因此ec a k c k k a k FR PQ 22)1()1(2||||2222==++=。

即证：||||FR PQ 为定值e2点评：一般地，圆锥曲线的离心率为 e （e>0），PQ 为过焦点 F 而不垂直于 F 所在的对称轴的弦，且 PQ 的中垂线交 x 轴于 R ，则必有eFR PQ 2||||=。

专题24 平面几何的定值问题【例题与求解】【例1】 如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值. 解题思路：线段的和差倍分考虑截长补短，利用圆的基本性质，证明三角形全等.P AB CD【例2】 如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （ ） A .到CD 的距离保持不变 B .位置不变C .等分DB⌒ D .随C 点的移动而移动 解题思路：添出圆中相关辅助线，运用圆的基本性质，用排除法得出结论.A【例3】 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.解题思路：不管ST 滑到什么位置，∠SOT 的度数是定值.从探寻∠SPM 与∠SOT 的关系入手.B【例4】 如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.解题思路：延长OG 交CD 于N ，利用题中的三等分点、平行四边形和三角形中位线的性质，实现把线段ON 转化成线段CH 的倍分关系，再以Rt △OND 为基础，通过勾股定理，使问题得以解决.BOACE HG D【例5】 如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发 生变化？若不变，求出比值；若变化，说明变化规律.解题思路：对于（3）从动点F 达到的特殊位置时入手探求定值.（图1） （图2）【能力训练】A 级1.如图，点A ，B 是双曲线xy 3=上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则=+21S S _______.AABCD EF（第3题图）（第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA，OB是⊙O任意两条半径，过B作BE⊥OA于E，又作OP⊥AB于P，则定值OP2+EP2为_________.4.如图，在菱形ABCD中，∠ABC=120°，F是DC的中点，AF的延长线交BC的延长线于点E，则直线BF与直线DE所夹的锐角的度数为（）A.30°B.40°C.50°D.60°5.如图，在⊙O中，P是直径AB上一动点，在AB同侧作AA'⊥AB，ABBB⊥'，且AA'=AP，BB'=BP.连接BA''，当点P从点A移动到点B时，BA''的中点的位置（）A．在平分AB的某直线上移动B.在垂直AB的某直线上移动C.在弧AMB上移动D.保持固定不移动AB'B（第5题图）（第6题图）6.如图，A，B是函数xky=图象上的两点，点C，D，E，F分别在坐标轴上，且分别与点A，B，O构成正方形和长方形.若正方形OCAD的面积为6，则长方形OEBF的面积是（）A.3B.6C.9D.127.（1）经过⊙O内或⊙O外一点P作两条直线交⊙O于A，B和C，D四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A，PB，PC，PD四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.⑥⑤④③②①)P (B )PB（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O 在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y=于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图） （第10题图） （第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证： （1）2222DK CK BK AK +++是定值； （2）2222DA CD BC AB +++是定值.B 级1.等腰△ABC 的底边BC 为定长2，H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时，面积S △ABC ·S △HBC 的值保持不变，则S △ABC ·S △HBC =________.2.已知A ，B ，C ，D ，E 是反比例函数xy 16=（x ＞0）图象上五个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是__________（用含π的代数式表示）.折叠，使点A ，B 落在六边形ABCDEF 的内部，记∠C ＋∠D ＋ ）A . ∠1＋∠2＝900°－2αB . ∠1＋∠2＝1080°－2αC . ∠1＋∠2＝720°－αD . ∠1＋∠2＝360°－21αPD CB A A（第3题图） （第4题图）4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在AB 上滚动，切点为T ，⊙O 交AO ，BO 于M ，N ，则弧MTN （ ）A .在0°到30°变化 B.在30°到60°变化 C .保持30°不变 D .保持60°不变5.如图，AB 是⊙O 的直径，且AB =10，弦MN 的长为8.若MN 的两端在圆上滑动时，始终与AB 相交，记点A ，B 到MN 的距离分别为h 1，h 2，则∣h 1-h 2∣等于（ ）A .5B .6C .7D .8（第5题图）6.如图，已知△ABC 为直角三角形，∠ACB =90°，AC =BC ，点A ，C 在x 轴上，点B 坐标为（3，m ）（m ＞0），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B ，D . （1）求点A 的坐标（用m 表示） （2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连接PQ 并延长交BC 于点E ，连接BQ 并延长交AC 于点F .试证明：FC （AC +EC ）为定值.7.如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A ，B 的点M .设直线AC 与BM 相交于K ，直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.（湖北省选拔赛试题）12GF ED CHBA B K MB AC H A（第7题图） （第8题图）8.如图，设H 是等腰三角形ABC 两条高的交点，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积S △ABC ·S △HBC 的值变小、变大，还是不变？证明你的结论.9.如图，在平面直角坐标系xOy 中，抛物线10941812--=x x y 与x 轴的交点为点A ，与y 轴的交点为点B .过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC .现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时，点Q 也同时停止运动.线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于E ，射线QE 交x 轴于点F .设动点P ，Q 移动的时间为t （单位：秒）. （1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程； （3）当290<<t 时，△PQF 的面积是否总是定值？若是，求出此值；若不是，请说明理由； （4）当t 为何值时，△PQF 为等腰三角形，请写出解答过程.（第9题图） （第10题图） 10.已知抛物线C 1：12121+-=x x y ，点F （1,1）. （1）求抛物线C 1的顶点坐标；（2）若抛物线C 1与y 轴的交点为A ，连接AF ，并延长交抛物线C 1于点B ，求证：211=+BFAF . （3）抛物线C 1上任意一点P （x P ，y P ）（0＜x P ＜1），连接PF ，并延长交抛物线C 1于点 Q （x Q ，y Q ），试判断211=+QFPF 是否成立？请说明理由.。