常规控制图的八种判异准则

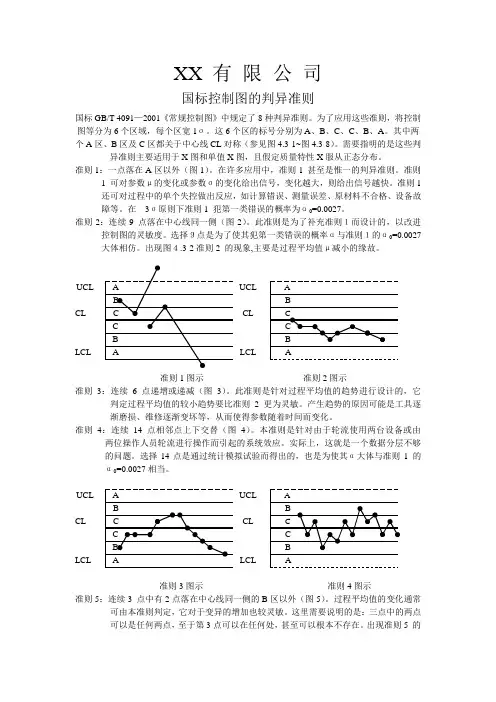
XX 有限公司国标控制图的判异准则国标GB/T 4091—2001《常规控制图》中规定了8种判异准则。

为了应用这些准则，将控制图等分为6个区域，每个区宽1σ。

这6个区的标号分别为A、B、C、C、B、A。

其中两个A区、B区及C区都关于中心线CL对称（参见图4.3-1~图4.3-8）。

需要指明的是这些判异准则主要适用于X图和单值X图，且假定质量特性X服从正态分布。

准则1：一点落在A区以外（图1）。

在许多应用中，准则1 甚至是惟一的判异准则。

准则1 可对参数μ的变化或参数σ的变化给出信号，变化越大，则给出信号越快。

准则1还可对过程中的单个失控做出反应，如计算错误、测量误差、原材料不合格、设备故障等。

在3σ原则下准则1 犯第一类错误的概率为α0=0.0027。

准则2：连续9 点落在中心线同一侧（图2）。

此准则是为了补充准则１而设计的，以改进控制图的灵敏度。

选择９点是为了使其犯第一类错误的概率α与准则１的α0=0.0027大体相仿。

出现图４.3-2准则2 的现象,主要是过程平均值μ减小的缘故。

UCL UCLCL CLLCL LCL准则1图示准则2图示准则3：连续6点递增或递减（图3）。

此准则是针对过程平均值的趋势进行设计的，它判定过程平均值的较小趋势要比准则 2 更为灵敏。

产生趋势的原因可能是工具逐渐磨损、维修逐渐变坏等，从而使得参数随着时间而变化。

准则4：连续14 点相邻点上下交替（图4）。

本准则是针对由于轮流使用两台设备或由两位操作人员轮流进行操作而引起的系统效应。

实际上，这就是一个数据分层不够的问题。

选择14点是通过统计模拟试验而得出的，也是为使其α大体与准则1 的α0=0.0027相当。

UCL UCLCL CLLCL LCL准则3图示准则4图示准则5：连续3 点中有2点落在中心线同一侧的B区以外（图5）。

过程平均值的变化通常可由本准则判定，它对于变异的增加也较灵敏。

这里需要说明的是：三点中的两点可以是任何两点，至于第3点可以在任何处，甚至可以根本不存在。

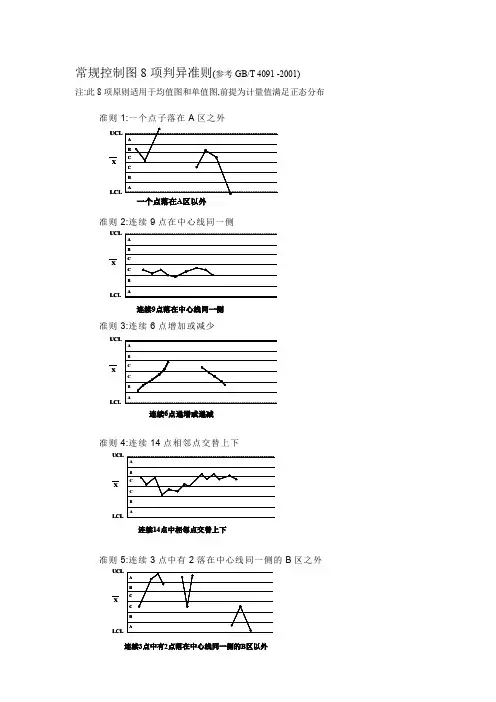
常规控制图8项判异准则(参考GB/T 4091 -2001) 注:此8项原则适用于均值图和单值图,前提为计量值满足正态分布
准则1:一个点子落在A 区之外
准则2:连续9点在中心线同一侧
准则3:连续6点增加或减少
准则4:连续14点相邻点交替上下
准则5:连续3点中有2落在中心线同一侧的B 区之外
UCL
LCL X 一个点落在A 区以外
UCL
LCL X 连续9点落在中心线同一侧
UCL
LCL X 连续6点递增或递减
UCL
LCL X
连续14点中相邻点交替上下UCL
LCL
X
连续3点中有2点落在中心线同一侧的B 区以外
准则6:连续5点中有4落在中心线同一侧的C 区之外
准则7:连续15点在C 区中心线内
准则8:连续8点在中心线两侧,却无一点在C 区
UCL
LCL X
连续5点中有4点落在中心线同一侧的C 区以外
UCL
LCL X
连续15点落在中心线两侧的C 区内UCL
LCL X
连续8点落在中心线两侧且无一点在C 区内。

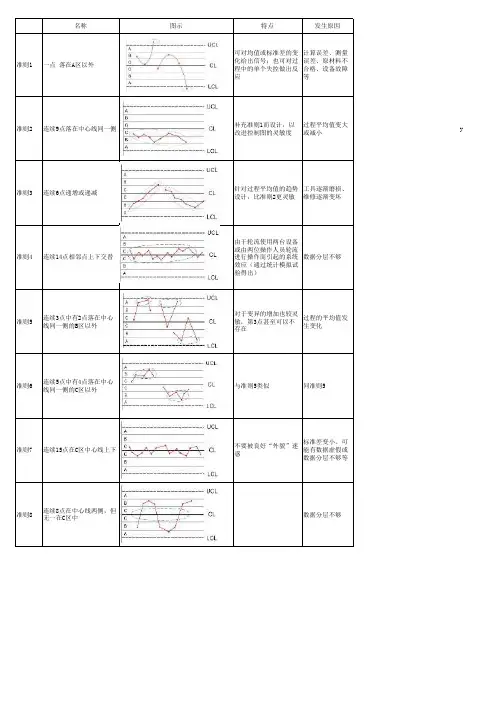
控制图判定异常情况的主要原理控制图通常要考察数据的位置、分布和排列情况来判断过程是否继续保持稳定或抑发生异常。

控制图判定异常情况的设计，是统计学家根据概率原理设计的，有充分的科学依据。

控制图判定异常通常都能找到可查明的原因，以便考虑采取措施。

为避免对异常情况判定的盲目性，此将判断的原理作初步分析。

控制图判定异常情况的主要原理是：1，“小概率事件实际上不发生”，如果概率很小的事发生了那就要分析原因了，小概率“小”到多少呢，要具体分析，一般说发生概率在0.01%以下，就应考虑了。

2，计量值一般服从正态分布的随机规律，其主要是：（1）在平均值两边随机分布，各占约50%，表现了强烈的对称性；（2）±1西格玛区间分布占68%，即有约2/3的值应在±1西格玛区间内，表现了相对集中性；（3）±2西格玛区间分布占95%，即在±2西格玛区间外的值约不到5%；（4）±3西格玛区间外的值只有不到0.3%，也就是“小概率”，几乎不应发生；3，其他破坏随机分布的情形。

如相当多的值连续上升的情况等等。

控制图判定异常情况的主要情况有：1，点子出了控制界限。

稳定合格的控制图，控制界限在规格范围里面，凡在控制界限内的点都在规格范围内，解决了合格性的问题。

如果点子出了控制界限，稳定性出了问题；如果点子甚至出了规格范围，那就是合格性出了问题。

点子出控制界限的概率是不到0.3%，如果时不时就出界，就破坏了正态分布的规律，判定异常就无疑了。

但如果是偶而出界，例如：35个点以上有一个出界，100点有两个出界，1/35=2.8%，2/100=2.0%，和0.3%差异不到一个数量级，那就有可能是正常现象（特别是出界不多的情形），具体问题要具体分析。

2，而要解决其稳定性，主要是通过观察点子的分布和排列情况来判断。

如果分布和排列情况发生了异常的变化，也就是其稳定性受到破坏，也就要发出警告。

一般说分布和排列情况发生的异常有下列几种情况：（将以中心线为对称的上下控制线均匀分为6个小区（一个小区相当于1 s），以中心线为对称的两个小区分别称C，B，A区，靠着中心线两边的小区称C区，稍外的两区称B区，最外的两区称A区。

控制图分类和判异规则控制图（ControlChart）⼜叫管制图，是对过程质量特性进⾏测定、记录、评估，从⽽监察过程是否处于控制状态的⼀种⽤统计⽅法设计的图。

图上有三条平⾏于横轴的直线：?中⼼线（CL，CentralLine）、上控制线（UCL，UpperControlLine）?和?下控制线（LCL，LowerControlLine）?，并有按时间顺序抽取的样本统计量数值的描点序列。

UCL、CL、LCL统称为控制线（ControlLine），通常控制界限设定在±3标准差的位置。

根据?控制图使⽤⽬的不同，控制图可分为：分析⽤控制图和控制⽤控制图?。

根据统计数据的类型不同，控制图可分为：计量控制图和计数控制图（包括计件控制图和计点控制图）。

计量型控制图平均数与极差控制图(-X-RChart)平均数与标准差控制图(-X-SChart)中位数与极差控制图(~X-RChart)个別值与移动极差控制图(X-Rm?Chart)计数值控制图不良率控制图(Pchart)不良数控制图(nPchart，⼜称npchart或dchart)缺点数控制图(Cchart)单位缺点数控制图(Uchart)控制图种类及应⽤场合控制图的分析与判定应⽤控制图的⽬的，就是要及时发现过程中出现的异常，判断异常的原则就是出现了“⼩概率事件”，为此，判断的准则有两类。

?第⼀类：点⼦越出界限的概率为0.27%。

准则1属于第⼀类。

第⼆类：点⼦虽在控制界限内，但是排列的形状有缺陷。

准则2-8属于第⼆类。

控制图⼋⼤判异准则（⼝诀）?2/3A?（连续3点中有2点在中⼼线同⼀侧的B区外<即a区内>）4/5C?（连续5点中有4点在中⼼线同⼀侧的C区以外）6连串?（连续6点递增或递减，即连成⼀串）8缺C?（连续8点在中⼼线两侧，但没有⼀点在C区中）9单侧?（连续9点落在中⼼线同⼀侧）14交替?（连续14点相邻点上下交替）15全C?（连续15点在C区中⼼线上下，即全部在C区内1界外?（1点落在A区以外）?2/3A（连续3点中有2点在中⼼线同⼀侧的B区外<即a区内>）判读：1、控制过严；2、材料品质有差异；3、检验设备或⽅法之⼤不相同；4、不同制程之资料绘于同⼀控制图上；5、不同品质材料混合使⽤。

【SPC 8种波动】SPC 8种波动的检验标准是什么？导语：SPC 8种波动，即八种判断异常的检验准则，每一种检验准则代表一种异常现象，应用SPC 控制图进行过程评估与监控，首先应掌握此八种波动检验模式《常规控制图》国家标准GB/T4091——2001明确给出了变差的可查明原因的八种波动模式，那么SPC 8种波动的检验标准是什么？下面我们将做详细介绍：图示：SPC 8种波动的检验标准是什么？SPC控制图检验1：1个点落在A区以外检验1给出了对控制图的基本解释：点出界就判异。

当过程处于统计控制状态时，点子落在控制限内的概率为99.73%，落在控制限外的概率为1-99.73%=0.27%。

检验1可以对过程中的单个失控做出反应，如计算、测量误差、原材料不合格、设备故障等。

SPC控制图检验2：连续9点落在中心线同一侧当过程处于统计控制状态时，连续9点落在中心线同一侧的概率为P（连续9点落在中心线同一侧）=2*（0.5）9=0.003906=0.3906%即虚发报警的概率为0.3906%，第一类错误的概率为α=0.3906%。

在SPC控制图中心线同一侧连续出现的点成为链，链可能位于中心线的上测也可能位于中心线的下侧。

注意：连必须由“连续”出现的点子构成。

链中包含的点子数目成为链长。

链长≥9，判断出现了异常。

连续9点落在中心线同一侧”判断出现异常的一个重要原因是：模式2的α=0.3906%与“点出界就判异”的模式1的α=0.27%最接近。

出现检验2此种模式，主要是过程平均值减小的缘故。

SPC控制图检验3：连续6点递增或递减当过程处于统计控制状态时，连续6点递增或递减的概率为P（连续6点递增或递减）=0.2733%即须发报警的概率为0.2733%，第一类错误的概率为α=0.2733%。

点子逐点上升或下降的状态称为倾向或趋势。

注意，递减的下降倾向，后面的点子一定要低于或等于前面的点子，否则倾向中断，需要重新计算。

控制图判定异常情况的主要原理控制图通常要考察数据的位置、分布和排列情况来判断过程是否继续保持稳定或抑发生异常。

控制图判定异常情况的设计，是统计学家根据概率原理设计的，有充分的科学依据。

控制图判定异常通常都能找到可查明的原因，以便考虑采取措施。

为避免对异常情况判定的盲目性，此将判断的原理作初步分析。

控制图判定异常情况的主要原理是：1，“小概率事件实际上不发生”，如果概率很小的事发生了那就要分析原因了，小概率“小”到多少呢，要具体分析，一般说发生概率在0.01%以下，就应考虑了。

2，计量值一般服从正态分布的随机规律，其主要是：（1）在平均值两边随机分布，各占约50%，表现了强烈的对称性；（2）±1西格玛区间分布占68%，即有约2/3的值应在±1西格玛区间内，表现了相对集中性；（3）±2西格玛区间分布占95%，即在±2西格玛区间外的值约不到5%；（4）±3西格玛区间外的值只有不到0.3%，也就是“小概率”，几乎不应发生；3，其他破坏随机分布的情形。

如相当多的值连续上升的情况等等。

控制图判定异常情况的主要情况有：1，点子出了控制界限。

稳定合格的控制图，控制界限在规格范围里面，凡在控制界限内的点都在规格范围内，解决了合格性的问题。

如果点子出了控制界限，稳定性出了问题；如果点子甚至出了规格范围，那就是合格性出了问题。

点子出控制界限的概率是不到0.3%，如果时不时就出界，就破坏了正态分布的规律，判定异常就无疑了。

但如果是偶而出界，例如：35个点以上有一个出界，100点有两个出界，1/35=2.8%，2/100=2.0%，和0.3%差异不到一个数量级，那就有可能是正常现象（特别是出界不多的情形），具体问题要具体分析。

2，而要解决其稳定性，主要是通过观察点子的分布和排列情况来判断。

如果分布和排列情况发生了异常的变化，也就是其稳定性受到破坏，也就要发出警告。

一般说分布和排列情况发生的异常有下列几种情况：（将以中心线为对称的上下控制线均匀分为6个小区（一个小区相当于1 s），以中心线为对称的两个小区分别称C，B，A区，靠着中心线两边的小区称C区，稍外的两区称B区，最外的两区称A区。

控制图八大判异准则－精简顺口溜版口决：（就三句，很简单吧！只要记住以下兰色部分的三句话就行 23456，AC连串串（连增或连减）； 81 514，缺C全C交替转； 9单侧，一点在外。

控制图八大判异准则提练（口决、图片对应项目）： 1、2/3A（连续3点中有2点在中心线同一侧的B区外<即A区内>） 2、4/5C（连续5点中有4点在中心线同一侧的C区以外） 3、6连串（连续6点递增或递减，即连成一串） 4、8缺C（连续8点在中心线两侧，但没有一点在C区中） 5、9单侧（连续9点落在中心线同一侧） 6、14交替（连续14点相邻点上下交替） 7、15全C（连续15点在C区中心线上下，即全部在C区内） 8、1界外（1点落在A区以外） 解说： 23456，AC连串串（连增或连减）； 2/3、4/5、6分别对应A、C、连串串；即2/3A；4/5C；6连串。

81514，缺C全C交替转 8、15、14分别对应缺C、全C、交替转；即8缺C；15全C；14上下交替。

9单侧，一点在外 9点在同一侧；一点出A区外。

转自学易网 转自学易网 控制图八大判异学，易网准则－精简顺口溜版口决：（就三句，很简单吧！只要记住以下兰色部23456，AC连串串（连增或连减）；81 514，缺C全C交替转；9单侧，一点在外。

控制图八大判异准则提练（口决、图片对应项目）：1、2/3A（连续3点中有2点在中心线同一侧的B区外<即A区内>）2、4/5C（连续5点中学，易网有4点在中心线同一侧的C区以外）3、6连串（连续6点递增或递减，即连成一串）4、8缺C（连续8点在中心线两侧，但没有一点在C区中）5、9单侧（连续9点落在中心线同一侧）6、14交替（连续14点相邻点上下交替）7、15全C（连续15点在C区中心线上下，即全部在C区内）8、1界外（1点落在A区以外）解说：23456，AC连串串（连增或连减）；2/3、4/5、6分别对应A、C、连串串；即2/3A；4/5C；6连串。

控制图八大判异准则
1、2/3A（连续3点中有2点在中心线同一侧的B区外<即A区内>）
2、4/5C（连续5点中有4点在中心线同一侧的C区以外）
3、6连串（连续6点递增或递减，即连成一串）
4、8缺C（连续8点在中心线两侧，但没有一点在C区中）
5、9单侧（连续9点落在中心线同一侧）
6、14交替（连续14点相邻点上下交替）
7、15全C（连续15点在C区中心线上下，即全部在C区内）
8、1界外（1点落在A区以外）
判稳原则（3选1即可）：
1. 控制图上连续25个点，界外点数为0，在这种情况下，过程稳定但被判为不稳定的可能性只有0.0654；
2. 控制图上连续35个点，界外点数不多于1，在这种情况下，过程稳定但被判为不稳定的可能性只有0.0041；
3. 控制图上连续100个点，界外点数不多于2，在这种情况下，过程稳定但被判为不稳定的可能性只有0.0026。

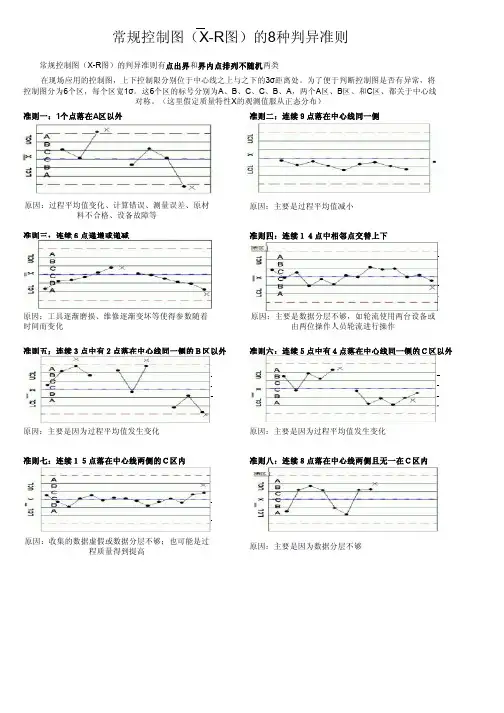
WECO Rule 判异准则
WECO Rule判异准则是用于控制图判断的一套规则，包括点出界和界内点排列不随机两类判异准则。

这些准则主要适用于均值图和单值X图。

并假定质显特性X服从正态分布。

在实际应用中，经常使用的判异准则具有明显物理意义。

当过程处于统计受控状态时，所有的判异准则都是针对变异的。

具体来说，在常规控制图中规定了8种判异准则，并将控制图等分为6个区域，每个区宽1σ，这些区域的标号分别为A、B. C. C、B. A,其中两个A区、B区及C区都关于中心线CL对称。

在使用这些判异准则时，需要注意对点子的数目未加限制，故原则上可以有很多种模式，但实际应用中仅采用具有明显物理意义的若干种。

制定：审核：批准：。

控制图八大判异准则－精简顺口溜版控制图八大判异准则－精简顺口溜版口决：（就三句，很简单吧！只要记住以下兰色部分的三句话就行了，不过第一次要对照下面附件中的图看才明白。

）23456，AC连串串（连增或连减）；81514，缺C全C交替转；9单侧，一点在外。

控制图八大判异准则提练（口决、图片对应项目）：1、2/3A（连续3点中有2点在中心线同一侧的B区外<即A区内>）2、4/5C（连续5点中有4点在中心线同一侧的C区以外）3、6连串（连续6点递增或递减，即连成一串）4、8缺C（连续8点在中心线两侧，但没有一点在C区中）5、9单侧（连续9点落在中心线同一侧）6、14交替（连续14点相邻点上下交替）7、15全C（连续15点在C区中心线上下，即全部在C区内）8、1界外（1点落在A区以外）解说：23456，AC连串串（连增或连减）；---2/3、4/5、6分别对应A、C、连串串；即2/3A；4/5C；6连串。

81514，缺C全C交替转---8、15、14分别对应缺C、全C、交替转；即8缺C；15全C；14上下交替。

9单侧，一点在外---9点在同一侧；一点出A区外。

第四节控制图1控制图——过程控制的工具。

用来表示一个过程特性的图象。

它有两个基本用途：①用来判断过程是否一直受统计控制。

②用来帮助过程保持受控状态。

2控制图的构成：UCLCLLCL取样时间①收集：收集数据并画在图上。

②控制：根据过程数据计算试验控制线识别变差特殊原因并采取措施。

③分析及改进：确定普通变差的大小，并采取减少它的措施。

重复三个阶段，从而不断改进过程。

3控制图的益处：①供正在进行过程控制的操作者使用。

②有助于过程在质量上和成本上能持续地、可预见的保持下去。

③使过程达到：——更高的质量。

——更低的单件成本。

——更高的有效能力。

④为讨论过程的性能提供共同的语言。

⑤区分变差的特殊原因和普通原因，作为采取局部措施或对系统采取措施的指南。