苏科版初中数学七年级上册《3.6 整式的加减》同步练习卷

第三章 3.1列代数式 同步练习题

一、选择题

1．下列各式中,不是代数式的是( )

A．－557 B．3x－2y－1 C．π≈3.14 D.sv

2．用代数式表示：a的2倍与3的和．下列表示正确的是( )

A．2a－3 B．2a＋3 C．2(a－3) D．2(a＋3)

3．－a(a是有理数)表示的数是( )

A．正数 B．负数 C．正数或负数 D．任意有理数

4．用式子表示“比a的平方的一半小1的数”是( )

A．(12a)2－1 B.12a2－1 C.12(a－1)2 D．(12a－1)2

5．两个数的和是30,其中一个数用字母x表示,那么另外一个数是( )

A．30x B．30＋x C．x－30 D．30－x

6．若a,b,c表示三个有理数,则下列等式可以表示乘法交换律的是( )

A．a＋b＝b＋a B．(a＋b)＋c＝a＋(b＋c)

C．ab＝ba D．c(a＋b) ＝ca＋cb

7．一个三位数的各数位上的数字之和等于12,且个位数字为a,十位数字为b,则这个三位数可表示为( )

A．12＋10b＋a B．12 000＋10b＋a

C．112＋10b＋a D．100(12－a－b)＋10b＋a

8．若三角形的一条边长为a,这条边上的高为h,则这个三角形的面积S可以表示为( )

A.ha B．a＋h C．ah D.12ah

x x x x x 北师大版数学七年级上册 3.4 整式的加减

一、选择题

1．下列各式中是多项式的是 （ ）

A.21 B.yx C.3ab D.22ba

2．下列说法中正确的是（ ）

A.x的次数是0

B.y1是单项式

C.21是单项式 D.a5的系数是5

3．如图1，为做一个试管架，在acm长的木条上钻了4个圆孔，每个孔直径2cm，则x 等于

（ ）

A.58acm B.516acm C.54acm D.58acm

4．)()(cadcba( )

A. bd B.db C.db D. db

5．只含有zyx,,的三次多项式中，不可能含有的项是 （ ）

A.32x B.xyz5 C.37y D.yzx241

6．化简 )]72(53[2baaba的结果是 （ ）

A.ba107 B.ba45 C.ba4 D.ba109

二、填空题

7.单项式853ab的系数是

,次数是 .

8.144mnmn= ；

9.计算：22224(2)(2)abababab ； 图 1

10.规定一种新运算:1bababa,如1434343,请比较大小:34 43(填“>”、“=”或“>”).

初中-数学-打印版

初中-数学-打印版 苏科版数学七年级上册同步练习

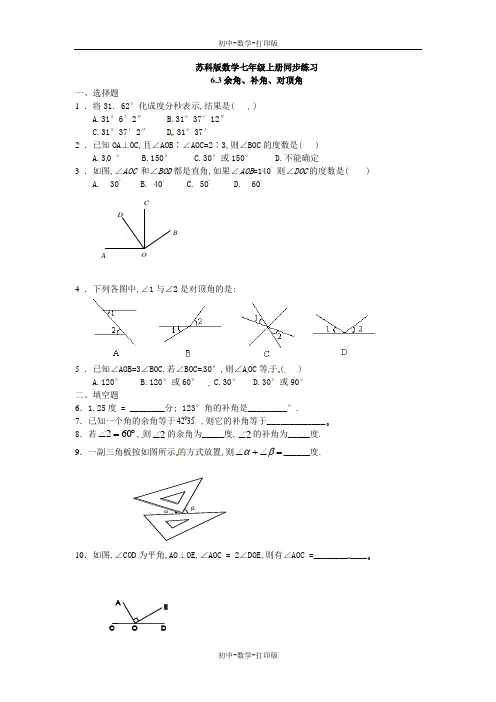
6.3余角、补角、对顶角一、选择题

1 ．将31. 62°化成度分秒表示,结果是( )

A.31°6′2″ B.31°37′12″C.31°37′2″ D.31°37′

2 ．已知OA⊥OC,且∠AOB∶∠AOC=2∶3,则∠BOC的度数是( )

A.30 ° B.150° C.30°或150° D.不能确定3 ．如图,∠AOC 和∠BOD都是直角,如果∠AOB=140◦ 则∠DOC的度数是( )

A. 30◦ B. 40◦ C. 50◦ D. 60◦

ODCBA

4 ．下列各图中,∠1与∠2是对顶角的是:

5 ．已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC等于( )

A.120° B.120°或60° C.30° D.30°或90°

二、填空题6．1.25度 = ________分; 123°角的补角是_________°.

7．已知一个角的余角等于'03542 ,则它的补角等于_____________｡

8．若602,则2的余角为_____度,2的补角为_____度.9．一副三角板按如图所示的方式放置,则______度.

10．如图,∠COD为平角,AO⊥OE,∠AOC = 2∠DOE,则有∠AOC =____________｡

αβ

EADOC 初中-数学-打印版

初中-数学-打印版

11．如图,在∠AOD的内部作射线OB,使∠AOB=∠COD,则图中还有哪些相等的角____________________.

OACD三、解答题

12．由图填空:⑴∠AOC=_________+___________;

⑵∠AOC-∠AOB=____;⑶∠COD=∠AOD-___;

北师大版七年级数学上册第3章《整式及其加减》同步练习及答案—3.3整式（2）

一．判断题

(1)31x是关于x的一次两项式． ( )

(2)－3不是单项式．( )

(3)单项式xy的系数是0．( )

(4)x3＋y3是6次多项式．( )

(5)多项式是整式．( )

二、选择题

1．在下列代数式：21ab，2ba，ab2+b+1，x3+y2，x3+ x2－3中，多项式有（ ）

A．2个 B．3个 C．4个 D5个

2．多项式－23m2－n2是（ ）

A．二次二项式 B．三次二项式 C．四次二项式 D五次二项式

3．下列说法正确的是（ ）

A．3 x2―2x+5的项是3x2，2x，5

B．3x－3y与2 x2―2xy－5都是多项式

C．多项式－2x2+4xy的次数是３

D．一个多项式的次数是6，则这个多项式中只有一项的次数是6

4．下列说法正确的是（ ）

A．整式abc没有系数 B．2x+3y+4z不是整式

C．－2不是整式 D．整式2x+1是一次二项式

5．下列代数式中，不是整式的是（ ）

A、23x B、745ba C、xa523 D、－2005

6．下列多项式中，是二次多项式的是（ ）

A、132x B、23x C、3xy－1 D、253x

7．x减去y的平方的差，用代数式表示正确的是（ ）

A、2)(yx B、22yx C、yx2 D、2yx

8．某同学爬一楼梯，从楼下爬到楼顶后立刻返回楼下。已知该楼梯长S米，同学上楼速度是a米/分,下楼速度是b米/分,则他的平均速度是（ ）米/分。

A、2ba B、bas C、bsas D、bsass2 9．下列单项式次数为3的是( )

x x x x x 新课标北师大版数学七年级上册同步测试题

3.4 整式的加减

一、选择题

1．下列各式中是多项式的是 （ ）

A.21 B.yx C.3ab D.22ba

2．下列说法中正确的是（ ）

A.x的次数是0

B.y1是单项式

C.21是单项式 D.a5的系数是5

3．如图1，为做一个试管架，在acm长的木条上钻了4个圆孔，每个孔直径2cm，则x 等于 （ ）

A.58acm B.516acm C.54acm D.58acm

4．)()(cadcba( )

A. bd B.db C.db D. db

5．只含有zyx,,的三次多项式中，不可能含有的项是 （ ）

A.32x B.xyz5 C.37y D.yzx241

6．化简 )]72(53[2baaba的结果是 （ ）

A.ba107 B.ba45 C.ba4 D.ba109

二、填空题

7.单项式853ab的系数是

,次数是 .

8.144mnmn= ； 图 1

9.计算：22224(2)(2)abababab ；

10.规定一种新运算:1bababa,如1434343,请比较大小:34 43(填“>”、“=”或“>”).

人教版七年级数学上册2.2整式的加减 同步练习卷

一、选择题

1.下列各式不是同类项的是（ ）

A．ba2与ba221 B．x21与-3xC．ba231与251ab D．xy41与yx

2.下列各组中的两式是同类项的是（ ）

A．32与3n B．ba254与ca254

C．2x与2 D．nm31.0与321nm

3.下列各式中，与yx2是同类项的是（ ）

A．2xy B．xy2 C．yx2 D．223yx

4.计算3a2－a2的结果是（ ）

A.4a2 B.3a2 C.2a2 D.3

5.下列式子中正确的是（ ）

A．abba33 B．143mnmn

C．4221257aaa D．2229495xyxyxy

6.计算－3(x－2y)＋4(x－2y)的结果是（ ）

A.x－2y B.x＋2y C.﹣x－2y D.﹣x＋2y

7.一个单项式减去22yx等于22yx，则这个单项式是（ ）

A．22x B．22y C．22x D．22y

8.化简yxyx的最后结果是（ ）

A．0 B．x2 C．y2 D．yx22

9.减去x32等于8362xx的代数式是（ ）

A．1062xx B．1062xC．662x D．162xx

10.已知：222232,232babaBbabaA则AB等于（ ）

A．252bab B．254babC．252bab D．254bab

11.当a是整数时，多项式77323aaa与32323aaa的和一定是（ ）

A．3的倍数 B．4的倍数

人教版七年级数学上册2.2整式的加减 同步练习卷

一、选择题

1.下列各式不是同类项的是（ ）

A．ba2与ba221 B．x21与-3xC．ba231与251ab D．xy41与yx

2.下列各组中的两式是同类项的是（ ）

A．32与3n B．ba254与ca254

C．2x与2 D．nm31.0与321nm

3.下列各式中，与yx2是同类项的是（ ）

A．2xy B．xy2 C．yx2 D．223yx

4.计算3a2－a2的结果是（ ）

A.4a2 B.3a2 C.2a2 D.3

5.下列式子中正确的是（ ）

A．abba33 B．143mnmn

C．4221257aaa D．2229495xyxyxy

6.计算－3(x－2y)＋4(x－2y)的结果是（ ）

A.x－2y B.x＋2y C.﹣x－2y D.﹣x＋2y

7.一个单项式减去22yx等于22yx，则这个单项式是（ ）

A．22x B．22y C．22x D．22y

8.化简yxyx的最后结果是（ ）

A．0 B．x2 C．y2 D．yx22

9.减去x32等于8362xx的代数式是（ ）

A．1062xx B．1062xC．662x D．162xx

10.已知：222232,232babaBbabaA则AB等于（ ）

A．252bab B．254babC．252bab D．254bab

11.当a是整数时，多项式77323aaa与32323aaa的和一定是（ ）

A．3的倍数 B．4的倍数

2.2 整式的加减

一．填空题

1．已知单项式与是同类项，则=

.

2.

在代数式4x2-8x+5-3x2+6x-2中，4x2和 是同类项，-8x和 是同类项，-2和 也是同类项。

3．三个连续奇数中，最小的一个是2n﹣1，则这三个连续奇数的和是 ．

4．若关于a,b的多项式(a2+2ab-b2)-(a2+mab+2b2)中不含ab项,则m = .

5.计算： ；

6．已知s+t=22，3m﹣2n=8，则多项式2s+4.5m﹣（3n﹣2t）的值为 ．

7.化简 ．

二．选择题

8．若m﹣x=2，n+y=3，则（m﹣n）﹣（x+y）=（ ）

A．﹣1 B．1 C．5 D．﹣5

9.计算2-2(1-a)的结果是 ( )

A.a B.-a C.2a D.-2a

10．下列各式合并同类项结果正确的是（ ）

A．3x2﹣x2=3 B．3a2﹣a2=2a2 C．3a2﹣a2=a D．3x2+5x3=8x5

11． 下列各组单项式中，为同类项的是（ ）

A.a3与a2 B.- a2与2a2

C.2xy与2x D.﹣3与a

12．如果单项式x2ym+2与xny的和仍然是一个单项式，则m．n的值是（ ）

A．m=2，n=2 B．m=﹣1，n=2 C．m=﹣2，n=2 D．m=2，n=﹣1

13.下列合并同类项正确的是（ ）

A.

B. C.

D.

14．合并同类项m﹣3m+5m﹣7m+…+2013m的结果为（ ）

A．0 B．1007m C．m D．以上答案都不对

15．已知4n﹣m=4，则（m﹣4n）2﹣3（m﹣4n）﹣10的值是（ ）

********灿若寒星竭诚为您提供优质文档*********

灿若寒星

第2课时 整式的加减

一、选择题

1．下列整式加减运算中，结果正确的是( )

A．7a－8b＝－1

B．－3a＋8a＝11a

C．－6ab－(－7ab)＝－ab

D．3a2b－(－8a2b)＝11a2b

2．化简(2x－3y)－3(4x－2y)的结果为( )

A．－10x－3y B．－10x＋3y

C．10x－9y D．10x＋9y

3．设M＝2a－3b，N＝－2a－3b，则M＋N等于( )

A．4a－6b B．4a

C．－6b D．4a＋6b ********灿若寒星竭诚为您提供优质文档*********

灿若寒星 4．减去－2x等于－3x2＋4x＋1的多项式是( )

A．－3x2＋2x＋1 B．3x2－2x－1

C．－3x2＋1 D．3x2＋1

5．一个代数式的2倍与－2a＋b的和是a＋2b，这个代数式是( )

A．3a＋b B．－12a＋12b

C.32a＋32b D.32a＋12b

6．已知某学校有(5a2＋4a＋27)名学生正在参加植树活动，为了支援兄弟学校，决定从中抽调(5a2＋7a)名学生前去支援，则该校剩余的学生人数是( )

A．－3a－27 B．－3a＋27

C．－11b＋27 D．11a－27

7．一个长方形的一边长为2a＋3b，另一边长为a＋b，则这个长方形的周长是( )

A．12a＋16b B．6a＋8b C．3a＋4b D．2a2＋5ab＋3b2

8．若A，B都是五次多项式，则A＋B是( )

A．五次多项式

B．四次多项式

C．次数不低于五次的多项式 ********灿若寒星竭诚为您提供优质文档*********

灿若寒星 D．次数不高于五次的多项式或单项式

9．2017·上杭期末 若(a＋1)2＋|b－2|＝0，化简a(x2y＋xy2)－b(x2y－xy2)的结果为( )

初中数学试卷

灿若寒星整理制作

3.6整式的加减同步练习

姓名_____________班级____________学号____________分数_____________

一、选择题

1 ．化简221aa的结果是( )

A.41a B.41a C.1 D.1

2 ．当,1m时22242mmm等于( )

(A)-7 (B)3 (C)1 (D)2

3 ．当2x时,代数式13bxax的值为6,那么当2x时13bxax的值为( )

A、6 B、-4 C、5 D、1

4 ．下列运算正确的是( )

A.5a2-3a2=2 B.2a2+3a2=5a4

C.3a+2b=5ab D.7ab-6ab=ab

5 ．如果1ab,且,ab都是整数,则ab的值为 ( )

A 0 B 1 C 1 D 1

6 ．下列运算中,正确的是 （ ）

A. 325abab B. 323323

C. 22321xx D. (3)(4)1

7 ．已知3257xy,那么代数式15102xy的值为( )

A 8 B 10 C 12 D 35

8 ．当1x时,代数式31mxnx的值为2008,则当1x时,代数式31mxnx的值为

A 2006 B 2007 C -2008 D - 2009

9 ．若51nm,那么)mn(3的值是( )

教学准备

1. 教学目标

教学目标

知识与技能：

①理解同类项的概念；

②掌握合并同类项的方法；

③会利用合并同类项将整式化简求值；

④会运用整式的加减解决简单的实际问题；

⑤通过类比数的运算探究合并同类项的法则，从中体会数式通性和类比的数学思想。

过程与方法：

①通过小组讨论、合作学习等方式，经历概念的形成过程；

②培养学生自主探索知识和合作交流的能力。

情感态度与价值观 ：

①初步体会数学和人类生活的密切联系；

②通过交流讨论活动，培养学生主动和他人合作的意识。

2. 教学重点/难点

教学重点/难点

教学重点

①理解同类项的概念，掌握合并同类项的法则；

②会利用合并同类项将整式化简求值。

教学难点

①根据同类项的概念，在多项式中找到同类项；

②掌握合并同类项的方法，会利用合并同类项将整式化简求值。

3. 教学用具 4. 标签

教学过程

教学过程

1 问题引入

问题一：在西宁到拉萨路段，列车在冻土地段的行驶速度是100 km/h，在非冻土地段的行驶速度是120 km/h，列车通过非冻土地段所需时间是通过冻土地段所需时间的2.1倍，如果通过冻土地段需要t h，你能用含t的式子表示这段铁路的全长吗？

问题二：整式的运算是建立在数的运算基础之上的，对于有理数的运算是怎样做的呢？

问题三：整式的运算与有理数的运算有什么联系？

【教师说明】总结同学们的答案，得出用含t的式子表示这段铁路的全长：100t 这个式子的结果是352t.在这里我们可以用类比的算法计算这个多项式。同学们可以用有理数的运算规律进行整式的运算。例如计算100×2+252×2 =（100+252） 704；100 ；则100t+252t=(100+252)t=352t.

2 巩固练习

练习1 类比式子的运算，化简下列式子：

3 同类项概念引入

（1）上述各多项式的项有什么共同特点？

人教版七年级数学第二章整式的加减单元练习（含答案）

一、单选题

1．单项式 的系数和次数分别是（ ）

A.2，2 B.2，3 C.3，2 D.2，4

2．下列说法正确的是（ ）

A．ab+c是二次三项式

B．多项式2x2+3y2的次数是4

C．0是单项式

D．34ba是整式

3．下列各式中，代数式有（ ）个

（1）a+b=b+a;（2）1;（3）2x-1 ;（4）23xx;（5） s  r 2;（6） 6k

A．2 B．3 C．4 D．5

4．a的5倍与b的和的平方用代数式表示为（ ）

A．（5a+b）2 B．5a+b2 C．5a2+b2 D．5（a+b）2

5．下列各式中，不是整式的是（ ）．

A．3a B．2x  1 C．0 D．xy

6．23-xyz的系数和次数分别是（ ）

A．系数是0，次数是5 B．系数是1，次数是6

C．系数是-1，次数是5 D．系数是-1，次数是6

7．考试院决定将单价为a元的统考试卷降价20%出售，降价后的销售价为（ ）

A．20%a B．20%a C．(120%)a D．(120%)a

8．有理数a，b在数轴上对应点的位置如图所示，则aabba化简后的结果是（ ）

A．a B．b C．2a+b D．2b−a

9．……依次观察左边三个图形,并判断照此规律从左到右第2019个图形是 （ ） A． B． C． D．

10．把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为a厘米，宽为b厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（ ）

A．4a厘米 B．4b厘米 C．2（a+b）厘米 D．4（a-b）厘米

11．使方程3x  5y  2  3kx  4k  0不含 x 的项，则 k 的值为（ ）

人教版数学七年级上册第2章整式的加减单元检测卷（含答案解析）

一．填空题（共6小题，满分24分，每小题4分）

1．（4分）将多项式x2y﹣2x3+7﹣5xy按字母x降幂排列为 ．

2．（4分）“x2的3倍与y的倒数的和”，用代数式表示为 ．

3．（4分）如图是一个数值转换机的示意图．当输入x＝3时，则输出的结果为 ．

4．（4分）如果x2﹣3xy＝6，3xy+y2＝10，则x2+y2＝ ．

5．（4分）当a＝3.6，b＝6.4时，求多项式a2+ab﹣b2+a﹣a2﹣ab+b+b2＝ ．

6．（4分）当3x+3﹣x＝2时，代数式32x+3﹣2x的值是 ．

二．选择题（共10小题，满分30分，每小题3分）

7．（3分）下列各式：﹣mn，m，8，，x2+2x+6，，，y3﹣5y+中，整式有（ ）

A．3个 B．4个 C．6个 D．7个

8．（3分）下列说法错误的是（ ）

A．x是单项式

B．3x4是四次单项式

C．的系数是

D．x3﹣xy2+2y3是三次多项式

9．（3分）三个连续整数的积是0，则这三个整数的和是（ ）

A．﹣3 B．0 C．3 D．﹣3或0或3

10．（3分）下列各式合并同类项后，结果正确的是（ ）

A．3a+2b＝5ab B．3x3y2﹣2x2y＝xy

C．3x2+2x3＝5x5 D．4x2y﹣7yx2＝﹣3x2y

11．（3分）下列说法中，错误的是（ ）

A．x2是二次单项式

B．x3﹣2xy2+y3是三次三项式 C．0是单项式

D．﹣的系数是﹣1

12．（3分）若﹣3x2my3与2x4yn的和是一个单项式，则|m﹣n|的值是（ ）

A．0 B．1 C．7 D．﹣1

13．（3分）若A＝3m2﹣5m+2，B＝3m2﹣5m﹣2，则A与B的大小关系是（ ）

A．A＝B B．A＞B C．A＜B D．无法确定

14．（3分）将2（x+y）+3（x+y）﹣4（x+y）合并同类项，得（ ）

人教版初中数学七年级上册第二章《整式的加减》 单元测试

一、选择题（每题3分，共30分）

1.下列说法正确的是（ ）

A.a的系数是0 B.1y是一次单项式 C.－5x的系数是5 D.0是单项式

2.下列单项式：①312a2b；②－2x1y2；③－32x2；④－1a2b.其中书写不正确的有（ ）

A.1个 B.2个 C.3个 D.4个

3.下列各组中的两项，不是同类项的是（ ）

A.a2b与－6ab2 B.－5x3y与934yx3 C.2πR与π2R D.－35与53

4.下列说法正确的是（ ）

A.整式就是多项式 B.π是单项式 C.x4+2x3是七次二项次 D.315x是单项式

5.不改变多项式3b3－2ab2+4a2b－a3的值，把后三项放在前面是“－”号的括号中，正确的是（ ）

A.3b3－(2ab2－4a2b+a3) B.3b3－(2ab2+4a2b+a3)

C.3b3－(－2ab2+4a2b－a3) D.3b3－(2ab2+4a2b－a3)

6.若m，n都是正整数，多项式xm+yn+3m+n的次数是（ ）

A.2m+2n B.m或n C.m+n D.m，n中的较大数

7.张老板以每颗a元的单价买进水蜜桃100颗，现以每颗比单价多两成的价格卖出70颗后，再以每颗比单价低b元的价格将剩下的30颗卖出，那么全部水蜜桃共卖（ ）元

A.70a+30(a－b) B.70×(1+20%)×a+30b

C.100×(1+20%)×a－30(a－b) D.70×(1+20%)×a+30(a－b)

8.在一定条件下，若物体运动的路程s(m)与时间t(s)的关系式为s＝5t2+2t，则当t＝6秒时，该物体所经过的路程为（ ）

一、选择题

1．某养殖场2018年年底的生猪出栏价格是每千克a元．受市场影响，2019年第一季度出栏价格平均每千克下降了15%，到了第二季度平均每千克比第一季度又上升了20%，则第三季度初这家养殖场的生猪出栏价格是每千克( )

A．(1-15%)(1＋20%)a元 B．(1-15%)20%a元 C．(1＋15%)(1-20%)a元 D．(1＋20%)15%a元

2．已知322xy和m2xy是同类项，则式子4m24的值是（ ）

A．21 B．12 C．36 D．12

3．把有理数a代数410a得到1a，称为第一次操作，再将1a作为a的值代入410a得到2a，称为第二次操作，...，若a=23，经过第2020次操作后得到的是（ ）

A．-7 B．-1 C．5 D．11

4．大于1的正整数m的三次幂可“裂变”成若干个连续奇数的和，如3235，337911，3413151719，．若3m“裂变”后，其中有一个奇数是2019，则m的值是（ ）

A．43 B．44 C．45

D．55

5．如图，填在下面各正方形中的4个数之间都有相同的规律，根据此规律，m的值是（ ）

A．38 B．52 C．74 D．66

6．已知有理数1a,我们把11a称为a的差倒数,如:2的差倒数是1112,1的差倒数是11112.如果12a,2a是1a的差倒数,3a是2a的差倒数,4a是3a的差倒数…依此类推,那么2020a的值是（ ）

A．2 B．13 C．23 D．32

7．已知单项式2x3y1+2m与3xn+1y3的和是单项式，则m﹣n的值是（ ）

A．3 B．﹣3 C．1 D．﹣1

8．下面去括号正确的是（ ）

A．2()2yxyyxy B．2(35)610aaaa

C．()yxyyxy D．222()2xxyxxy

1．在代数式a2+1，﹣3，x2﹣2x，π，1x中，是整式的有（ ）

A．2个 B．3个 C．4个 D．5个C

解析：C

【分析】

单项式和多项式统称为整式，分母中含有字母的不是整式.

【详解】

解：a2+1和 x2﹣2x是多项式，-3和π是单项式，1x不是整式，∵单项式和多项式统称为整式，∴整式有4个.

故选择C.

【点睛】

本题考查了整式的定义.

2．下列代数式的书写，正确的是（ ）

A．5n B．n5 C．1500÷t D．114x2yA

解析：A

【分析】

直接利用代数式书写方法分析得出答案．

【详解】

解：A、5n，书写正确，符合题意；

B、n5，书写错误，不合题意；

C、1500÷t，应为1500t，故书写错误，不合题意；

D、114x2y=54x2y，故书写错误，不合题意；

故选：A．

【点睛】

此题主要考查了代数式，正确把握代数式的书写方式是解题关键．

3．有一种密码，将英文26个字母,,,,abcz（不论大小写）依次对应1，2，3，…，26这26个序号（见表格），当明码对应的序号x为奇数时，密码对应的序号为|25|2x，当明码对应的序号x为偶数时，密码对应的序号为122x，按照此规定，将明码“love”译成密码是（ ）

字母 a b c d e f g h i j k l m 序号 1 2 3 4 5 6 7 8 9 10 11 12 13

字母

n o p q r s t u v w x y z

序号 14 15 16 17 18 19 20 21 22 23 24 25 26

A．love B．rkwu C．sdri D．rewjD

解析：D

【分析】

明码“love”中每一个字母所代表的数字分别为12，15，22，5，再根据这四个数字的奇偶性，求得其密码．

【详解】

l对应的序号12为偶数，则密码对应的序号为1212182，对应r；

o对应的序号15为奇数，则密码对应的序号为|1525|52，对应e；