(好题)初中数学七年级数学上册第三单元《整式及其运算》测试卷(含答案解析)(1)

《好题》小学数学四年级下册第三单元运算定律测试卷（含答案解析）(6)

一、选择题

1．25×13×4=13×（25×4）=1300，这里运用了（ ）。

A. 乘法交换律 B. 乘法结合律 C. 乘法交换律和乘法结合律

2．529+267+71+○，○里填（ ）时计算最简便。

A. 29 B. 133 C. 71 D. 104

3．76×98+2×76=76×100，这是运用( )进行计算的。

A. 乘法交换律 B. 乘法结合律 C. 乘法分配律

4．61×24 61×4×6， 里应该填( )。

A. > B. = C. <

5．下面没有运用乘法结合律的是（ ）。

A. a×4×25=a×（4×25） B. 4×35×25=4×25×35 C. 56×125=7×（8×125）

6．下面说法中错误的是（ ）。

A. 在研究平均数问题时可以用移多补少的方法

B. 我们在研究小数的意义时运用了数形结合的思想方法

一、选择题

1．在《九章算术》方田章“圆田术”中指出：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这里所用的割圆术所体现的是一种无限与有限的转化的思想，比如在234111112222…中，“…”代表按规律不断求和，设234111112222x．则有112xx，解得2x，故2341111122222．类似地2461111333的结果为（ ）

A．43 B．98 C．65 D．2

2．甲车队有汽车100辆，乙车队有汽车68辆，根据情况需要甲车队的汽车是乙车队的汽车的两倍，则需要从乙队调x辆汽车到甲队，由此可列方程为( )

A．100﹣x＝2(68+x) B．2(100﹣x)＝68+x

C．100+x＝2(68﹣x) D．2(100+x)＝68﹣x

3．在三峡大坝截流时，用载重卡车将一堆石料运到围堰龙口，第一次运了这堆石料的少万方，第二次运了剩下的多万方，此时还剩下万方未运，若这堆石料共有万方，于是可列方程为（ ）

A．

B．

C．

D．

4．甲乙两人骑摩托车从相距170千米的A，B两地相向而行，2小时相遇，如果甲比乙每小时多行5千米，则乙每小时行（ ）

A．30千米 B．40千米 C．50千米 D．45千米

5．互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（ ）

A．120元 B．100元 C．80元 D．60元

6．关于x的方程2xm3=1的解为2，则m的值是（ ）

A．2.5 B．1 C．-1 D．3

7．下列方程中，其解为﹣1的方程是（ ） A．2y=﹣1+y B．3﹣y=2 C．x﹣4=3 D．﹣2x﹣2=4

8．某校在举办“读书月”的活动中，将一些图书分给了七年一班的学生阅读，如果每人分3本，则剩余20本：如果每人分4本，则还缺25本．若设该校七年一班有学生x人，则下列方程正确的是( )

《好题》小学数学六年级上册第二单元位置与方向（二）测试卷（含答案解析）(7)

一、选择题

1．芳芳家在红红家北偏西40°的方向上，那么红红家在芳芳家（ ）的方上．

A. 北偏西40° B. 南偏北40° C. 南偏东40° D. 北偏东40°

2．小明面朝正北方向站立，向左转55°后所面向的方向是（ ）

A. 北偏东55° B. 北偏西55° C. 南偏东55° D. 南偏西55°

3．学校在图书馆的东偏南35°的方向上，图书馆在学校的（ ）的方向上。

A. 北偏西55° B. 西偏北55° C. 东偏南35° D. 南偏东55°

4．商场在学校北偏东30°的方向上，那么学校在商场（ ）的方向上。

A. 东偏北30° B. 南偏西30° C. 西偏南30°

5．小丽先向东偏北45°的方向走了50 m，又向南偏东45°的方向走了50 m，她现在的位置在起点的（ ）方向。

A. 正东 B. 正北 C. 东北 D. 东南

《好题》小学数学四年级下册第三单元运算定律测试卷（答案解析）(7)

一、选择题

1．下面算式中，正确运用乘法分配律的是（ ）。

A. 25×（8+10）=25×8+10 B. 25×（8+10）=25×8×10

C. 25×（8+10）=25×8+25×10 D. 25×（8+10）=25×8+10×8

2．下面没有运用乘法结合律的是（ ）。

A. 2×（5×23）=（2×5）×23 B. 4×35×25=4×25×35 C. 56×125=7×（8×125）

3．与87×101的计算结果相等的式子是（ ）。

A. 87×100+1 B. 87×100-1 C. 87×100+87 D. 87×100×1

4．计算125×24时比较简便的方法是（ ）。

A. 125×8×3 B. 125×3×8×125 C. 125×20×4 D. 125×（8+3）

5．101×97和（ ）相等。

A. 100×97+97 B. 100+1×97 C. 100×97+1

6．与49×99的计算结果相等的式子是（ ）。

一、选择题

1．一串数字的排列规律是：第一个数是2，从第二个数起每一个数与前一个数的倒数之和为1，则第2020个数是（ ）

A．12

B．1

C．2 D．2

2．按照规律排列的一列数：-1，2，-4，8，-16，32，……则第2020个数应为（ ）．

A．20192 B．20192 C．20202 D．20202

3．在下列单项式中：①26x；②23xy； ③20.37yx； ④214y； ⑤213xy；⑥332，说法正确的是（ ）

A．②③⑤是同类项 B．②与③是同类项

C．②与⑤是同类项 D．①④⑥是同类项

4．若x≠-1，则把-11x称为x的“和1负倒数”，如：2的“和1负倒数”为-13，-3的“和1负倒数”为12，若123x，2x是1x的“和1负倒数”，3x是2x的“和1负倒数”，…依此类推，则2020x的值为（ ）

A．23 B．-35 C．75 D．-52

5．如图，用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形，三角形、正方形的每一边用一根火柴棒．如果搭这两个图案一共用了2030根火柴棒，且正方形的个数比三角形的个数的少4个，则搭成的三角形的个数是（ ）

A．429 B．409 C．408 D．404

6．小张在做数学题时，发现了下面有趣的结果

321

87654

1514131211109

242322212019181716

……

根据以上规律可知，第20行左起第一个数是（ ）

A．360 B．339 C．440 D．483

7．下列计算正确的有（ ）

①224； ②2224abab； ③211525； ④202011；

⑤aa．

A．1个 B．2个 C．3个 D．4个

8．若代数式2226231xaxbxx(,ab为常数)的值与字母x的取值无关，则代数式2ab的值为（ ）

一、选择题

1．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．按这样的方法继续下去，第n个图形中有（ ）个三角形（用含n的代数式表示）．

A．4n B．41n C．41n D．43n

2．元旦，是公历新一年的第一天“元旦”一词最早出现于《晋书》：“颛帝以孟夏正月为元，其实正逆元旦之春”．中国古代间以腊月、十月等的月首为元旦．1949年中国华人民共和国以公历1月1日为元旦，因此元旦在中国也被称为“阳历年”．为庆祝元旦，人民商场举行促销活动，促销的方法是“消费超过100元时，所购买的商品按原价打8折后，再减少20元”．若某商品的原价为x元（100x），则购买该商品实际付款的金额（单位：元）是（ ）

A．80%20x B．80%20x C．20%20x D．20%20x

3．任意大于1的正整数m的三次幂均可“分裂”成m个连接奇数的和，如：3235，337911，3413151719，…按此规律，若3m分裂后，其中一个奇数是2021，则m的值是（ ）

A．46 B．45 C．44 D．43

4．列式表示“x的3倍与y的平方的和”正确的是（ ）

A．223xy B．23()xy C．23xy D．2(3)xy

5．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为（ ）

A．2n﹣3 B．4n﹣1 C．4n﹣3 D．4n﹣2

6．如图，从边长为4cma的正方形纸片中剪去一个边长为1cma的正方形0a，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的周长为（ ）

A．28cma B．38cma C．415cma D．416cma

一、选择题

1．任意大于1的正整数m的三次幂均可“分裂”成m个连接奇数的和，如：3235，337911，3413151719，…按此规律，若3m分裂后，其中一个奇数是2021，则m的值是（ ）

A．46 B．45 C．44 D．43

2．如图为OABC、、、四点在数轴上的位置图，其中O为原点，且1AC，OAOB，若点C所表示的数为x，则点B所表示的数为（ ）

A．(1)x B．(1)x C．1x D．1x

3．如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为1n，每个数是它下一行左右相邻两数的和，则第8行第3个数（从左往右数）为（

）

A．160 B．1168 C．1252 D．1280

4．若a是最大的负整数，b是绝对值最小的有理数，c是倒数等于它本身的自然数，则代数式201520172016abc的值为（ ）

A．2014 B．2016 C．2或0 D．0

5．已知3ab，2cd，则acbd的值是（ ）

A．5 B．5 C．1 D．1

6．求23201312222的值，可令220131222S，则23201422222S，因此2014221SS．仿照以上推理，计算出23201315555的值为（ ）

A．201451 B．201351 C．2014514 D．2013514

7．如图，将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，剪的次数记为n，得到的正三角形的个数记为na，则2020a（ ）

A．6053 B．6058 C．6061 D．6062

8．甲、乙、丙三人进行骑自行车比赛，三人的骑行情况如下表：

甲 一半路程速度为6/ms，一半路程速度为4/ms

12022-2023学年七年级数学上册第三章《整式及其加减》测试卷

一、单选题

1．填在下面各正方形中的四个数之间都有一定的规律，按此规律可得到abcd的值为（）

A．355B．356C．435D．436

2．若单项式25mxy与单项式2136nyx的和仍为单项式，则2mn的值为（）

A．6B．1C．3D．1

3．已知一个多项式与239xx的和等于2341xx，则这个多项式是（）

A．51xB．51xC．131xD．131x

4．下列结论正确的个数是（）

①2不是单项式

②多项式3527xyxy是三次三项式③232π

3abc的系数是2

3，次数是6

④233mn的次数为4

A．0个B．1个C．2个D．3个

5．多项式23211

3

32xyxy的次数为（）

A．5B．3C．7D．8

6．已知53xy

，则55xy

的值为（）

A．0B．2C．5D．8

7．一本笔记本的原价为a元，降价后每本比原来便宜了b元，小明买了4本这样的笔记本，则他一共花

费了（）

A．

44ab

元B．

4ab元C．

4ab元D．4b元

8．按如图所示的运算程序，当输入3x，6y

时，输出的结果为（）

2A．1B．6C．45D．81

9．若2

2m与3n

互为相反数，则mn的值是（）

A．8B．8C．9D．9

10．当=1x时，3238axbx的值为18，则1282ba的值为（）

A．40B．42C．46D．56

二、填空题

11．在式子1

x，1xy

，2022，a

，23xy，1

3x

中，整式的个数是______个．

12．已知520ab

，则27ab的值为___________

13．a，b两数平方的和除以3的商可以表示为______．

14．已知有理数a、b、c满足1,2,3abc，且abcabc

，则abc__________．

15．如关于x，y的多项式2347514xymxyyxy化简后不含二次项，则m

一、选择题

1．计算若3x，则5x的结果是（ ）

A．2 B．8 C．2 D．8

2．一串数字的排列规律是：第一个数是2，从第二个数起每一个数与前一个数的倒数之和为1，则第2020个数是（ ）

A．12 B．1 C．2 D．2

3．对于多项式534axbx，当1x时，它的值等于5，那么当1x时，它的值为（ ）

A．5 B．5 C．3 D．3

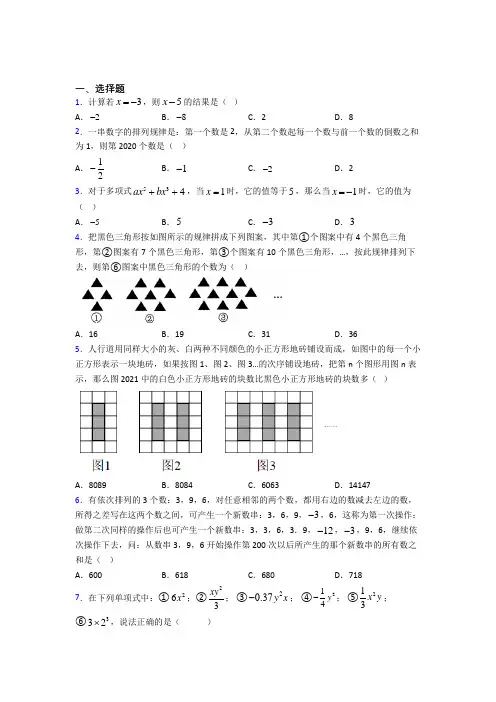
4．把黑色三角形按如图所示的规律拼成下列图案，其中第①个图案中有4个黑色三角形，第②图案有7个黑色三角形，第③个图案有10个黑色三角形，…，按此规律排列下去，则第⑥图案中黑色三角形的个数为（ ）

A．16 B．19 C．31 D．36

5．人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，如图中的每一个小正方形表示一块地砖，如果按图1、图2、图3…的次序铺设地砖，把第n个图形用图n表示，那么图2021中的白色小正方形地砖的块数比黑色小正方形地砖的块数多（ ）

A．8089 B．8084

C．6063 D．14147

6．有依次排列的3个数：3，9，6，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，3，6，这称为第一次操作：做第二次同样的操作后也可产生一个新数串：3，3，6，3．9，12，3，9，6，继续依次操作下去，问：从数串3，9，6开始操作第200次以后所产生的那个新数串的所有数之和是（ ）

A．600 B．618 C．680 D．718

7．在下列单项式中：①26x；②23xy； ③20.37yx； ④214y； ⑤213xy；⑥332，说法正确的是（ ） A．②③⑤是同类项 B．②与③是同类项

C．②与⑤是同类项 D．①④⑥是同类项

8．长度相同的木棒按一定规律拼搭图案，第1个需7根木棒，第2个需13根木棒，…，第11个需要木棒的个数为（ ）

一、选择题

1．如图为OABC、、、四点在数轴上的位置图，其中O为原点，且1AC，OAOB，若点C所表示的数为x，则点B所表示的数为（ ）

A．(1)x B．(1)x C．1x D．1x

2．将一根长为x cm的铁丝围成一个正方形，将它按如图所示的方式向外等距离扩2cm，得到新的正方形，则这根铁丝需要增加（ ）

A．8cm B．16cm C．(x+8)cm D．(x+16)cm

3．如图，从边长为4cma的正方形纸片中剪去一个边长为1cma的正方形0a，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的周长为（ ）

A．28cma B．38cma C．415cma D．416cma

4．如图，将一个边长为m的正方形纸片剪去两个小长方形，得到一个类似“9”的图案，再将剪下的两个小长方形无缝隙地拼成一个新的长方形，则新长方形的周长可表示为（ ）

A．59mn B．5.58mn C．45mn D．58mn

5．如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中①，②两张正方形纸片既不重叠也无空隙．已知①号正方形边长为a，②号正方形边长为b，则阴影部分的周长是（ ）

A．22ab B．42ab C．24ab D．33ab

6．如果12ax与21bxy是同类项，那么ab（ ）

A．2 B．3 C．4 D．5

7．有依次排列的3个数：3，9，6，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，3，6，这称为第一次操作：做第二次同样的操作后也可产生一个新数串：3，3，6，3．9，12，3，9，6，继续依次操作下去，问：从数串3，9，6开始操作第200次以后所产生的那个新数串的所有数之和是（ ）

A．600 B．618 C．680 D．718

一、选择题

1．如表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2018个格子中的整数为（

）

1 a b c 2 5 …

A．1 B．0 C．2 D．5

2．下面两个多位数1248624…，6248624…，都是按照如下方法得到的：从首位数字开始，将左边数字乘以2，若积为一位数，将其写在右边数位上，若积为两位数，则将其个位数字写在右边数位上．依次再进行如上操作得到第3位数字…后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，按如上操作得到一个多位数，则这个多位数前2020位的所有数字之和是（ ）

A．10091 B．10095 C．10099 D．10107

3．把黑色三角形按如图所示的规律拼成下列图案，其中第①个图案中有4个黑色三角形，第②图案有7个黑色三角形，第③个图案有10个黑色三角形，…，按此规律排列下去，则第⑥图案中黑色三角形的个数为（ ）

A．16 B．19 C．31 D．36

4．下列所给代数式中，属于单项式的是（ ）

A．a B．a C．12a D．2a

5．人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，如图中的每一个小正方形表示一块地砖，如果按图1、图2、图3…的次序铺设地砖，把第n个图形用图n表示，那么图2021中的白色小正方形地砖的块数比黑色小正方形地砖的块数多（ ）

A．8089 B．8084 C．6063 D．14147

6．已知整数1a，2a，3a，4a…满足下列条件：10a，211aa，322aa，433aa…依此类推，则2021a的值为（ ）

A．1010 B．1011 C．2021 D．2020 7．有依次排列的3个数：3，9，6，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，3，6，这称为第一次操作：做第二次同样的操作后也可产生一个新数串：3，3，6，3．9，12，3，9，6，继续依次操作下去，问：从数串3，9，6开始操作第200次以后所产生的那个新数串的所有数之和是（ ）

一、选择题

1．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．按这样的方法继续下去，第n个图形中有（ ）个三角形（用含n的代数式表示）．

A．4n B．41n C．41n D．43n

2．计算若3x，则5x的结果是（ ）

A．2 B．8 C．2 D．8

3．下列图形都是由同样大小的笑脸按一定的规律组成，其中第①个图形一共有2个笑脸，第②个图形一共有8个笑脸，第③个图形一共有18 个笑脸…按此规律，则第⑥个图形中笑脸的个数为（ ）

A．98 B．72 C．50 D．36

4．若代数式210kxyxky的值与x、y的取值无关，那么k的值为（ ）

A．0 B． C．1 D．1

5．如图，数轴上的三个点对应的数分别是a，a，b，化简abab的结果是（ ）

A．2a B．2a C．2b D．2b

6．单项式13mxy与4nxy是同类项，则nm的值是（ ）

A．1 B．3 C．6 D．8

7．下列说法正确的是（ ）

A．单项式x的系数是0

B．单项式﹣32xy2的系数是﹣3，次数是5

C．多项式x2+2x的次数是2 D．单项式﹣5的次数是1

8．观察下列等式：71＝7，72＝49，73＝343，74＝2401，75＝16807，76＝11649，…，那么：71＋72＋73＋…＋72022的末位数字是（ ）

A．0 B．6 C．7 D．9

9．下列图形都是由同样大小的矩形按一定的规律组成，其中，第1个图形中一共有6个矩形，第2个图形中一共有11个矩形，第3个图形中一共有16个矩形，…，按此规律，第7个图形中矩形的个数为（ ）

A．30 B．36 C．41 D．45

10．若代数式2226231xaxbxx(,ab为常数)的值与字母x的取值无关，则代数式2ab的值为（ ）

一、选择题

1．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．按这样的方法继续下去，第n个图形中有（ ）个三角形（用含n的代数式表示）．

A．4n B．41n C．41n D．43n

2．任意大于1的正整数m的三次幂均可“分裂”成m个连接奇数的和，如：3235，337911，3413151719，…按此规律，若3m分裂后，其中一个奇数是2021，则m的值是（ ）

A．46 B．45 C．44 D．43

3．下列各式的计算，正确的是（ ）

A．235abab B．2222yy C．1055ttt D．2232mnmnmn

4．求23201312222的值，可令220131222S，则23201422222S，因此2014221SS．仿照以上推理，计算出23201315555的值为（ ）

A．201451 B．201351 C．2014514 D．2013514

5．有依次排列的3个数：3，9，6，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，3，6，这称为第一次操作：做第二次同样的操作后也可产生一个新数串：3，3，6，3．9，12，3，9，6，继续依次操作下去，问：从数串3，9，6开始操作第200次以后所产生的那个新数串的所有数之和是（ ）

A．600 B．618 C．680 D．718

6．一个正方形的边长减少10%，则它的面积减少（ ）

A．19% B．20% C．1% D．10%

7．如图所示，直线,ABCD相交于点O，“阿基米德曲线”从点O开始生成，如果将该曲线与每条射线的交点依次标记为1,2,3,4,5,6…．那么标记为“2021”的点在（ ）

一、选择题

1．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．按这样的方法继续下去，第n个图形中有（ ）个三角形（用含n的代数式表示）．

A．4n B．41n C．41n D．43n

2．任意大于1的正整数m的三次幂均可以“拆解”成m个连续奇数的和，例如：3235，337911，3413151719，以此类推，现已知3m的“拆解数”中有一个数是2077，则m的值是（ ）

A．45 B．46 C．47 D．48

3．将连续正整数按如图所示的位置顺序排列：根据排列规律，则2021应在（ ）

A．A处 B．B处 C．C处 D．D处

4．已知3ab，2cd，则acbd的值是（ ）

A．5 B．5 C．1 D．1

5．如果12ax与21bxy是同类项，那么ab（ ）

A．2 B．3 C．4 D．5

6．如图所示，直线,ABCD相交于点O，“阿基米德曲线”从点O开始生成，如果将该曲线与每条射线的交点依次标记为1,2,3,4,5,6…．那么标记为“2021”的点在（ ）

A．射线OA上 B．射线OB上 C．射线OC上 D．射线OD上

7．如图，用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形，三角形、正方形的每一边用一根火柴棒．如果搭这两个图案一共用了2030根火柴棒，且正方形的个数比三角形的个数的少4个，则搭成的三角形的个数是（ ）

A．429 B．409 C．408 D．404

8．小张在做数学题时，发现了下面有趣的结果

321

87654

1514131211109

242322212019181716

……

根据以上规律可知，第20行左起第一个数是（ ）

A．360 B．339 C．440 D．483

一、选择题

1．任意大于1的正整数m的三次幂均可以“拆解”成m个连续奇数的和，例如：3235，337911，3413151719，以此类推，现已知3m的“拆解数”中有一个数是2077，则m的值是（ ）

A．45 B．46 C．47 D．48

2．单项式13mxy与4nxy是同类项，则nm的值是（ ）

A．1 B．3 C．6 D．8

3．若a是最大的负整数，b是绝对值最小的有理数，c是倒数等于它本身的自然数，则代数式201520172016abc的值为（ ）

A．2014 B．2016 C．2或0 D．0

4．如图，将一个边长为m的正方形纸片剪去两个小长方形，得到一个类似“9”的图案，再将剪下的两个小长方形无缝隙地拼成一个新的长方形，则新长方形的周长可表示为（ ）

A．59mn B．5.58mn C．45mn D．58mn

5．如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中①，②两张正方形纸片既不重叠也无空隙．已知①号正方形边长为a，②号正方形边长为b，则阴影部分的周长是（ ）

A．22ab B．42ab C．24ab D．33ab

6．已知整数1a，2a，3a，4a…满足下列条件：10a，211aa，322aa，433aa…依此类推，则2021a的值为（ ）

A．1010 B．1011 C．2021 D．2020

7．某水果商店在甲批发市场以每千克a元的价格购进30千克的橘子，又在乙批发市场以每千克b元（ba）的价格购进同样的50千克橘子．如果以每千克2ab元的价格全部卖出这种橘子，那么这家商店（ ）

A．盈利了 B．亏损了 C．不盈不亏 D．盈亏不能确定 8．按如图所示的运算程序，能使输出的结果为32的是（ ）

A．2x，4y B．2x，4y

C．4x，2y D．4x，2y

一、选择题

1．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．按这样的方法继续下去，第n个图形中有（ ）个三角形（用含n的代数式表示）．

A．4n B．41n C．41n D．43n

2．列式表示“x的3倍与y的平方的和”正确的是（ ）

A．223xy B．23()xy C．23xy D．2(3)xy

3．下列代数式中，全是单项式的一组是( )

A．1a，2，3ab B．2，a，12ab C．2ab，1，π D．x＋y，－1，13(x－y)

4．一串数字的排列规律是：第一个数是2，从第二个数起每一个数与前一个数的倒数之和为1，则第2020个数是（ ）

A．12 B．1 C．2 D．2

5．下面两个多位数1248624…，6248624…，都是按照如下方法得到的：从首位数字开始，将左边数字乘以2，若积为一位数，将其写在右边数位上，若积为两位数，则将其个位数字写在右边数位上．依次再进行如上操作得到第3位数字…后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，按如上操作得到一个多位数，则这个多位数前2020位的所有数字之和是（ ）

A．10091 B．10095 C．10099 D．10107

6．如果12ax与21bxy是同类项，那么ab（ ）

A．2 B．3 C．4 D．5

7．携带着2公斤珍贵月壤的嫦娥五号返回器于2020年12月17日凌晨1时32分，降落在内蒙古市四子王旗，实现了中国版的“空间跳跃”.在科幻电影《银河护卫队》中，星际之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成，如图所示，两个星球之间的路径只有一条，三个星际之间的路径有3条，四个星际之间的路径有6条，...，按此规律，则10个星际之间的路径有（ ）

A．45条 B．21条 C．42条 D．38条 8．下列运算正确的是（ ）