有限元极限分析法在边坡中的应用
- 格式:ppt
- 大小:26.85 MB
- 文档页数:56

岩质边坡稳定性分析计算引言:岩质边坡是指由岩石构成的边坡体,它的稳定性分析是地质工程中的一项重要内容。
本文将围绕岩质边坡的稳定性分析进行详细讨论,包括边坡的力学特性、稳定性分析的方法和计算步骤。
一、岩质边坡力学特性:岩质边坡的力学特性主要包括边坡坡度、岩性、结构构造、地质构造、坡面覆盖物、地下水等。
这些因素对边坡的稳定性有着重要影响。
1.边坡坡度:边坡坡度是指地面或水平面与边坡倾斜线的夹角,是影响边坡稳定性的重要因素。
坡度越大,边坡的稳定性越差。
2.岩性:岩石的强度、粘聚力、内摩擦角等岩性参数对边坡稳定性有着重要影响。
一般来说,岩性较强的边坡稳定性较好。
3.结构构造:边坡中的断层、节理、褶皱等结构构造对边坡的稳定性有着重要影响。
结构面的发育程度和倾角越大,边坡的稳定性越差。
4.地质构造:地质构造包括岩层倾角、层面、节理等,对边坡的稳定性具有重要影响。
地质构造的研究可以帮助我们了解边坡的受力特点和变形规律。
5.坡面覆盖物:坡面覆盖物通常包括土壤、草地、水层等,这些覆盖物的分布情况和特性对边坡的稳定性有着显著影响。
6.地下水:地下水的存在对边坡的稳定性具有重要影响。
当地下水位上升时,边坡会受到水的浸润,导致边坡强度降低,从而增加边坡失稳的可能性。
二、岩质边坡稳定性分析方法:岩质边坡的稳定性分析方法主要有极限平衡法和有限元法两种,下面将对这两种方法进行介绍。
1.极限平衡法:极限平衡法是一种经典的岩质边坡稳定性分析方法,它基于边坡体在其稳定状态下的力学平衡原理进行计算。
这种方法通常将边坡分割为无限小的切割体,并假设切割体沿着内摩擦边界面滑动,从而得到边坡的稳定状态。
2.有限元法:有限元法是一种基于有限元理论进行边坡稳定性分析的方法。
这种方法将边坡体离散为有限数量的单元,通过求解单元之间的位移和应力,得到边坡的稳定状态。
有限元法能够模拟较为复杂的边坡几何形状和边界条件,但计算复杂度较大。
三、岩质边坡稳定性计算步骤:进行岩质边坡稳定性分析计算时,通常需要进行以下步骤:1.边坡参数确定:根据实地调查和实验数据,确定边坡的坡度、坡高、岩石强度参数、结构面参数等。


边坡稳定有限元分析本例将演示如何使用有限元方法分析边坡稳定性并计算其安全系数。
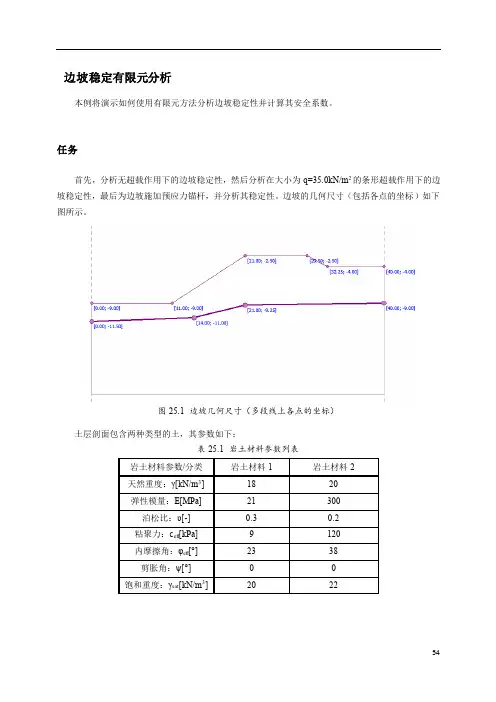
任务首先,分析无超载作用下的边坡稳定性,然后分析在大小为q=35.0kN/m2的条形超载作用下的边坡稳定性,最后为边坡施加预应力锚杆,并分析其稳定性。
边坡的几何尺寸(包括各点的坐标)如下图所示。
图25.1 边坡几何尺寸(多段线上各点的坐标)土层剖面包含两种类型的土,其参数如下:表25.1 岩土材料参数列表计算我们使用“GEO5岩土工程有限元分析计算模块”(以下简称“有限元模块”)(v18版)来分析该问题。
下面为建模和分析步骤:-建模阶段:分析设置和几何建模-工况阶段[1]:分析边坡无超载作用时的稳定性-工况阶段[2]:分析加入超载后边坡的稳定性-工况阶段[3]:分析加入锚杆后边坡的稳定性-结论建模阶段:分析设置和几何建模在分析设置界面中设置“分析类型”为“边坡稳定分析”,保持其他选项不变。
图25.2 【分析设置】界面注:选择“边坡稳定分析”时和选择“应力应变分析”时的设置以及建模过程几乎完全一样。
在【分析】界面点击“开始分析”按钮即可以分析并计算边坡的安全系数。
在“有限元-边坡稳定分析”模块中,各个工况阶段之间是相互独立的,即当前工况阶段的分析结果不受上一工况阶段分析结果的影响。
下一步,设置全局坐标范围。
设置的坐标范围要足够大,这样才能使得所要分析的区域不受边界条件的影响。
对于该算例,设置全局坐标范围<0m, 40m>,设置底边界距离多段线最低点距离为10m。
设置各个多段线和土层剖面,其参数如下表所示。
图25.3 全局坐标对话框表25.2各多段线及其节点的坐标列表设置各个岩土材料的参数并将其指定到相应的分区。
在本算例中,我们选择Drucker-Prager(DP)模型(见注)。
设置两种岩土材料的剪胀角ψ均为0°,即当材料受到剪力作用时,其体积不发生改变。
注:分析边坡稳定性时,必须选择非线性弹塑性模型作为岩土材料的本构模型,因为在边坡稳定分析过程中岩土材料会产生塑性应变,且塑性应变的产生是和岩土材料的强度参数c和φ相关的。

用ANSYS有限元法分析边坡稳定性的思考发布时间:2021-07-08T07:42:19.893Z 来源:《防护工程》2021年7期作者:陈洁[导读] :提出了ANSYS有限元法分析边坡稳定性的优点,使用ANSYS软件模拟典型天然边坡,为了提高仿真模拟的准确性和求解结果的准确度,提出在ANSYS软件中实体建模时在材料模型、几何模型和安全系数求解方面的思考。
针对实际边坡工程的ANSYS稳定性分析提出了一些问题和想法。
陈洁重庆交通大学河海学院重庆 400041摘要:提出了ANSYS有限元法分析边坡稳定性的优点,使用ANSYS软件模拟典型天然边坡,为了提高仿真模拟的准确性和求解结果的准确度,提出在ANSYS软件中实体建模时在材料模型、几何模型和安全系数求解方面的思考。
针对实际边坡工程的ANSYS稳定性分析提出了一些问题和想法。
关键词:边坡稳定;ANSYS;有限元1.ANSYS有限元法分析边坡稳定性的优点研究边坡稳定性问题可以大体分为极限平衡理论、室内模型研究和数值分析。
极限平衡理论不能考虑土体内部应力-应变的非线性关系,所求出的安全系数只能是假定滑落面的平均安全度。
求出的内力和反力不能代表实际产生的滑移变形的力,因此这个方法对于处理边坡稳定问题存在很大缺陷。
随着分析理论的不断完善,加之计算水平的不断发展,使有限元法有了越来越大的用武之地[1-2]。
用有限元研究边坡稳定性的优点如下:(1)破坏面的形状和位置不需要假定。
(2)有限元法有变形协调的本构关系。
(3)有限元法求解建议获得完整的应力、位移。
(4)有限元法可以考虑岩土体的不连续性,即非线性应力-应变。
2.ANSYS有限元法模拟边坡典型示例该边坡考虑弹性和塑性两种材料,边坡尺寸如图1所示。
图1边坡模型示意图计算模型为二维几何模型,模型先后建立了9个关键点、10条直线和3个面。
如图2所示。
图2 边坡网格模型示意图3.ANSYS实体建模中的思考尽管数值分析方法功能强大,但将其用于边坡稳定性分析现在也存在一些问题。


边坡稳定的有限元分析蓝杰;刘玉梅【摘要】In order to accurately grasped the stress characteristics of slope,this paper made stability analysis on the slope of highway using finite element strength reduction method,calculated the internal force of slope and the distribution situation of displacement,and determined the safety factor of slope.Finally compared the calculated results with the traditional method,demonstrated the feasibility of this method.%为准确掌握边坡的受力特点,采用有限元强度折减法对高速公路边坡进行了稳定性分析,计算得到边坡的内力和位移的分布情况,并确定出边坡的安全系数,最后将计算结果与传统方法进行了对比,表明了该方法的可行性。
【期刊名称】《山西建筑》【年(卷),期】2012(038)002【总页数】2页(P166-167)【关键词】边坡;有限元;强度折减法;稳定性;安全系数【作者】蓝杰;刘玉梅【作者单位】广西壮族自治区交通规划勘察设计研究院,广西南宁530011;广西壮族自治区交通规划勘察设计研究院,广西南宁530011【正文语种】中文【中图分类】TU413.62在公路建设中,不可避免的将修建边坡。
边坡的稳定性关系到道路工程的施工安全、建设成本和运营安全。
因此,保证边坡的稳定性对于防灾减灾、工程建设具有重要意义。
目前,边坡稳定性的分析方法有两类:极限平衡方法和数值分析方法。


露天矿边坡稳定性分析方法摘要:目前,随着我国基础建设事业的发展,越来越多的边坡工程开始出现。
随着露天矿山开采深度的增加,开挖扰动会导致岩体工程不断劣化,应力环境将会更加复杂,威胁到矿山生产的正常进行。
基于此,必须加强开挖扰动对露天矿边坡稳定性影响分析,以进一步保证矿山安全。
关键词:露天矿边坡;稳定性;安全因素引言在露天矿开采活动中,边坡失稳的现象非常常见,如不能得到妥善处理,很容易出现安全事故。
在本文中,笔者从露天矿边坡的特点入手,对影响露天矿边坡稳定性的安全因素展开分析,提出提升露天矿边坡稳定性的有效策略,为该方面的工作人员提供有价值的参考资料。
1露天矿边坡的特征1.1露天矿的边坡比较高,有些边坡在几十米到几百米之间,有些边坡甚至会达到数千米高,经过相应的观察可以发现,所揭露的岩层越多,那么边坡的差异就会越大,而且边坡也就会变得极为的复杂,岩体在暴露的过程中,整个岩体暴露的时间就会变得更长,而且岩体的完整性也比较差,岩体呈现出破碎性,经常相应的试验发现整个岩体的强度也是极低的。
1.2露天矿在形成的过程中,最终的边坡主要是从上部到下部逐渐的形成的,而且由于上部的年限比较长,在这种情况下就会缺乏稳定性,与此同时也具有着一定的时效性,从本质上来说,由于年限的不同,其边坡的上部和下部的稳定性也就存在着一系列的差异。
1.3露天矿场在开采的过程中,每一天都必须要进行穿孔、运输和爆破处理,这样就会产生一定的振动,对于周围的边坡是有着一定的影响的,在超出边坡承受范围的时候边坡的稳定性就会下降甚至出现一定的危险。
1.4边坡主要是由于露天矿体被不断的开采导致的,在这样的情况下,边坡的稳定性就在不断的变化,随着时间的推移和矿体的不断开采,边坡的稳定性会逐渐的下降。
1.5边坡的主要类型按照几何形状可以将其分为内陷边坡、倾斜边坡和外鼓边坡等,根据露天矿的坡体可以将其分为泥土边坡、岩石边坡、尾矿坡和构筑堆坡。
2影响露天矿边坡稳定性的安全因素2.1地质因素一是岩石性质与结构产生的影响。

土木工程中边坡稳定性分析方法在土木工程领域,边坡稳定性是一个至关重要的问题。
边坡的失稳可能会导致严重的人员伤亡和财产损失,因此,准确分析边坡的稳定性对于工程的安全和成功实施具有重要意义。
本文将探讨几种常见的土木工程中边坡稳定性分析方法。
一、定性分析方法1、工程地质类比法这是一种基于经验和对比的方法。
通过对已有的类似地质条件和边坡工程的研究和经验总结,来对新的边坡稳定性进行初步判断。
这种方法虽然简单快捷,但依赖于丰富的工程经验和大量的案例数据。
2、历史分析法通过研究边坡地区的历史地质活动、自然灾害记录以及以往的边坡变形破坏情况,来推断当前边坡的稳定性。
然而,这种方法受到历史资料完整性和准确性的限制。
二、定量分析方法1、极限平衡法这是目前应用较为广泛的一种方法。
它基于静力平衡原理,将边坡划分为若干个垂直条块,通过分析条块之间的力和力矩平衡,计算出边坡的安全系数。
常见的极限平衡法有瑞典条分法、毕肖普法等。
瑞典条分法假设滑动面为圆弧,不考虑条块间的作用力,计算较为简单,但结果相对保守。
毕肖普法考虑了条块间的水平作用力,计算结果更为精确,但计算过程相对复杂。
2、数值分析方法(1)有限元法将边坡离散为有限个单元,通过求解每个单元的应力和位移,来分析边坡的稳定性。
它可以考虑复杂的边界条件和材料非线性特性,能够更真实地模拟边坡的力学行为。
(2)有限差分法与有限元法类似,但采用差分格式来近似求解偏微分方程。
在处理大变形和复杂边界问题时具有一定的优势。
(3)离散元法特别适用于分析节理岩体等非连续介质的边坡稳定性。
它能够模拟块体之间的分离、滑动和碰撞等行为。
三、监测分析方法1、地表位移监测通过设置测量点,使用全站仪、GPS 等仪器定期测量边坡表面的位移变化。
当位移量超过一定的阈值时,提示边坡可能存在失稳风险。
2、深部变形监测采用钻孔倾斜仪、多点位移计等设备,监测边坡内部的深部变形情况。
这种方法能够更早地发现潜在的滑动面。
有限元强度折减法的原理、优点与超高边坡失稳的判据一、安全系数的定义两种方法可以导致边坡达到极限破坏状态,即:增量加载和折减强度。
传统边坡稳定分析中的安全系数是一个比值,假定一滑动面,根据力学的平衡来计算边坡安全系数,它等于滑动面以上土体条块的抗滑力与下滑力的比值。
式中K——安全系数;τ——滑动面上各点的实际强度。
将式子(4-1)两边同时除以k,上述公式变为其中:式(4-1)的左边等于I,表示滑坡体达到极限平衡状态,这意味着当代表强度的黏聚力和摩擦角被折减为1/K后,边坡最终到达破坏。
这个系数K就是有限元强度折减法中求解的安全系数,其实也就是强度折减系数。
二、有限元强度折减法的原理有限元强度折减法是在理想的弹塑性有限元计算中将边坡岩土体的抗剪强度参数:黏聚力c和内摩擦角φ按照安全系数的定义同时除以一个系数k,得到一组新的c′、φ′值,然后作为一组新的参数输入,再一次试算,如此循环。
当计算不收敛时,所对应的k被称为坡体的安全系数,此时边坡达到极限状态,将会发生剪切破坏,同时可以得到边坡的滑动面。
其中c′、φ′为三、有限元强度折减法的优点有限元强度折减分析法既具备了数值分析方法适应性广的优点,也具备了极限平衡法简单直观、实用性强的特点,目前被广大岩土工程师们广泛应用。
(1)不需要假定滑面的形状和位置,也无须进行条分。
只需要由程序自动计算出滑坡面与强度贮备安全系数。
(2)能够考虑“应力-应变”关系。
(3)具有数值分析法的各种优点,适应性强。
能够对各种岩土工程进行计算,不受工程的几何形状、边界条件等的约束。
(4)它考虑了土体的非线性弹塑性特点,并考虑了变形对应力的影响。
(5)能够考虑岩土体与支护结构的共同作用,并模拟施工过程和渐进破坏过程。
四、有限元强度折减法中超高边坡失稳的判据采用强度折减有限元方法分析超高边坡稳定性时,如何判断边坡是否达到极限平衡状态,十分关键。
这种有限元失稳判据的选取,没有获得共识,常见的失稳判据主要有下列三种。