岩土工程极限分析有限元法及其应用

基于有限元分析的岩土体力学参数反演方法研究岩土体力学是研究岩石和土壤的力学性质以及它们在地下工程中的行为的科学。

了解岩土体力学参数对于地质灾害风险评估和地下工程设计至关重要。

但是，对于复杂的岩土体结构或者无法直接获取参数的情况下，如何准确地反演岩土体力学参数一直是一个挑战。

有限元分析（Finite Element Analysis，FEA）是一种广泛应用于工程领域的数值分析方法，能够模拟和分析复杂结构的力学行为。

在岩土工程中，有限元分析常用于研究岩土体的变形、破裂、稳定性等问题，并可提供一些参数的估计。

基于有限元分析的岩土体力学参数反演方法针对这一问题发展起来。

一、反问题的数学描述岩土体力学参数反演可以看作是一个反问题，即从已知的观测数据反推出参数。

假设有一个岩土体结构，其初始参数未知。

通过采集实验数据或者在该结构上施加一定的加载，可以获得一些离散的观测值，如位移、应力或应变。

岩土体力学参数反演的目标是根据这些观测值推断出岩土体的参数。

二、参数反演方法1. 试-验法（试验与计算相结合）：通过实验数据的采集和有限元计算结果的拟合，逐步调整模型的参数，以使计算结果与实验数据相吻合，从而得到逼近真实参数的估计。

试-验法常用于实验室尺度或小尺度的岩土体参数反演研究。

2. 直接反演法（无试验数据）：直接反演法是在无试验数据的情况下通过有限元分析模拟建立拟合模型，再根据该模型计算岩土体的力学响应并反推参数。

这种方法需要准确的前提条件和丰富的先验知识，适用于已知结构和力学行为的情况。

3. 优化算法：基于有限元分析的优化算法是一种常用的参数反演方法。

它通过调整模型的参数，以最小化模拟结果与实验观测值之间的误差。

常见的优化算法包括遗传算法、粒子群算法等。

这些算法能够全局搜索参数空间，提高了反演结果的准确性和稳定性。

三、基于有限元分析的岩土体力学参数反演案例1. 地基承载力反演：地基承载力是地下工程中常关注的参数之一。

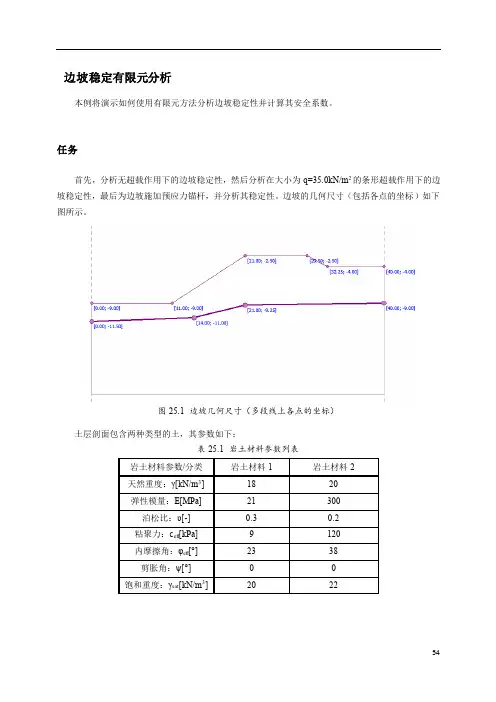
边坡稳定有限元分析本例将演示如何使用有限元方法分析边坡稳定性并计算其安全系数。

任务首先，分析无超载作用下的边坡稳定性，然后分析在大小为q=35.0kN/m2的条形超载作用下的边坡稳定性，最后为边坡施加预应力锚杆，并分析其稳定性。

边坡的几何尺寸（包括各点的坐标）如下图所示。

图25.1 边坡几何尺寸（多段线上各点的坐标）土层剖面包含两种类型的土，其参数如下：表25.1 岩土材料参数列表计算我们使用“GEO5岩土工程有限元分析计算模块”（以下简称“有限元模块”）（v18版）来分析该问题。

下面为建模和分析步骤：-建模阶段：分析设置和几何建模-工况阶段[1]：分析边坡无超载作用时的稳定性-工况阶段[2]：分析加入超载后边坡的稳定性-工况阶段[3]：分析加入锚杆后边坡的稳定性-结论建模阶段：分析设置和几何建模在分析设置界面中设置“分析类型”为“边坡稳定分析”，保持其他选项不变。

图25.2 【分析设置】界面注：选择“边坡稳定分析”时和选择“应力应变分析”时的设置以及建模过程几乎完全一样。

在【分析】界面点击“开始分析”按钮即可以分析并计算边坡的安全系数。

在“有限元-边坡稳定分析”模块中，各个工况阶段之间是相互独立的，即当前工况阶段的分析结果不受上一工况阶段分析结果的影响。

下一步，设置全局坐标范围。

设置的坐标范围要足够大，这样才能使得所要分析的区域不受边界条件的影响。

对于该算例，设置全局坐标范围<0m, 40m>，设置底边界距离多段线最低点距离为10m。

设置各个多段线和土层剖面，其参数如下表所示。

图25.3 全局坐标对话框表25.2各多段线及其节点的坐标列表设置各个岩土材料的参数并将其指定到相应的分区。

在本算例中，我们选择Drucker-Prager（DP）模型（见注）。

设置两种岩土材料的剪胀角ψ均为0°，即当材料受到剪力作用时，其体积不发生改变。

注：分析边坡稳定性时，必须选择非线性弹塑性模型作为岩土材料的本构模型，因为在边坡稳定分析过程中岩土材料会产生塑性应变，且塑性应变的产生是和岩土材料的强度参数c和φ相关的。

边坡稳定性评价方法综述摘要：随着岩土工程技术的进步，涌现了许多新的边坡稳定性分析方法，本文梳理了常见的边坡稳定性分析方法，分析与归纳各类评价方法的优缺点与适用条件，为合理选择边坡稳定性评价方法提供借鉴。

关键词：边坡稳定性，评价方法1引言随着人类工程活动对工程地质条件改造的日趋频繁和范围的不断扩展，在露天矿开采、水利水电、陆地交通和城市开发建设等方面都出现了大量的边坡工程。

边坡稳定性问题一直是岩土工程的一个重要研究内容，而边坡稳定性评价结果的正确与否直接关系到边坡工程的成败。

本文在分析总结近年来边坡稳定性评价方法的基础上，对边坡稳定性评价方法进行分类，旨在为合理选择边坡稳定性评价方法提供借鉴。

2边坡稳定性评价方法分类边坡稳定性评价应分析边坡的变形破坏模式，确定不同评价方法的适用范围与条件，才能对边坡工程的设计与施工恰当地选用评价方法提供指导意义。

传统的边坡稳定性评价方法分为两大类：定性评价方法与定量评价方法。

3定性评价方法工程地质定性分析法是边坡稳定性评价中起源最早，主要用于工程早期确定方案时的一种定性评价方法。

工程地质定性分析法以岩土工程勘察资料为基础，分析边坡岩土体的地质成因，筛选出影响边坡稳定性的主要因素，建立边坡工程地质模型，推测其可能的变形破坏模式，定性评价稳定性及其演变趋势。

对于地质条件相对简单的岩土质边坡，该法可直接得出可供工程设计和施工使用的结论；对于地质条件相对复杂的情形，该法在确定滑坡模式和变形机制方面具有明显优势，可为进一步定量计算边坡稳定性奠定基础。

定性评价方法中最常用的为工程地质类比法和边坡稳定性图解法。

3.1工程地质类比法工程地质类比法属于定性分析，其内容有历史分析法、因素类比法、类型比较法和边坡评比法等。

该方法主要通过岩土工程勘察，首先对工程地质条件进行分析。

如对有关地层岩性、地质构造、地形地貌等因素进行综合调查、分类，对已有的边坡破坏现象进行广泛的调查研究，了解其成因、影响因素、发展规律等；并分析研究工程地质因素的相似性和差异性；然后结合所要研究的边坡进行对比，得出稳定性分析和评价结果。

岩土边坡稳定性的影响因素及分析方法作者：陈琴来源：《科技创新与应用》2015年第35期摘要：在现代工程项目建设过程中，需要对岩土边坡的稳定性进行有效地分析，这样才能确保建筑主体结构的安全。

当前在对岩土边坡稳定性进行分析时采用的分析方法具有多样性的特点，因此，需要针对基本原理和适用范围来选择科学、合理的分析方法，有效地降低自然灾害所带来的危害。

文章分析了岩土边坡稳定性的主要影响因素，并进一步对岩土边坡稳定性的常用分析方法进行了具体的阐述。

关键词：岩土工程；边坡稳定性；影响因素；分析方法引言在各类工程项目建设中，由于建筑主体结构自身的重量，再加之受到外力作用，在其共同作用下，岩土边坡的稳定性会受到较大的影响。

这就需要对岩土边坡的变化情况进行有效控制，避免其对建筑的安全性和可靠性带来不利影响。

当构造物建设在岩土边坡上面时，实体表面的平稳性会受到较大的影响，由于构造物处于倾斜状态，这样在其使用年限不断延长的情况下下，避免不了会出现的滑动趋势，一旦这种滑动力超出主体结构的承担范围，则会导致滑坡事故的发生。

所以在一些岩土边坡所占比例较大的区域进行工程项目建设时，需要合理分析边坡的稳定性，选择科学的分析方法，并将其在工程项目整体建设工作中进行有效地应用。

而且在全面对岩土边坡稳定性进行分析的基础上，工程技术人员能够制定有效地防范措施，从而有效地降低或是避免滑坡等自然灾害的发生。

1 岩土边坡稳定性的主要影响因素1.1 内部因素1.1.1 边坡岩土体的类型和性质岩土体边坡的稳定性会受到边坡岩土体类型和性质差异的影响，不同的边坡岩土体类型和性质，其内部所能够承载的作用力也会有所差异，这样对边坡所带来的破坏形式也会具有较大的不同。

1.1.2 边坡的地质构造岩土边坡稳定性受到地质构造所带来的影响是多方面的，其表现形式也具有多样化的特点，如构造面的发育程度、形状、规模、连通性、内部填充物成分和程序等都会对岩土边坡的稳定性带来不同的影响，即使同一地质构造下其所对岩土边坡稳定性带来的影响也会存在一定的差异，受边坡倾斜度影响较大。

路堤边坡稳定性计算方法路堤边坡稳定性分析一直是岩土工程中的重要研究领域，目前边坡稳定性分析计算方法主要可以分为两大类，即极限平衡法和有限元（或有限差分）分析计算方法。

在极限平衡分析方法中，以安全系数来评价边坡的稳定性，其原理简单，物理意义明确，是最重要、最常用和最直观的稳定性评价指标。

所以计算边坡的安全系数是边坡稳定性分析的重要内容。

边坡稳定性分析是一个超静定问题，无法直接由静力平衡条件得出边坡的安全系数。

为了回避岩土的复杂应力应变关系并将超静定问题转化为静定问题，需对边坡的稳定性分析问题进行适当近似假定，使问题变得静定可解，从而形成了极限平衡分析方法。

这种处理方法使问题的严密性受到了一定的降低，但是，对计算结果的精度影响并不大，并且其优点是显而易见的，如使分析计算工作简化从而减少计算时间，因而在工程中获得广泛应用。

极限平衡方法的基本特点是：只考虑静力平衡条件和土的Mohr-Coulomb破坏准则，也就是说，通过分析土体在破坏那一刻的力的平衡来求解。

安全系数的定义：目前采用的安全系数主要有3种：(1)强度储备安全系数，其通过降低岩土体强度来得到边坡的安全系数；(2)超载储备安全系数，通过增大外部荷载计算边坡的安全系数；(3)下滑力超载储备安全系数，即只增大边坡的下滑力而不改变相应的抗滑力计算滑坡推力设计值。

极限平衡法主要采用强度储备安全系数的概念。

当安全系数为1时,边坡抗滑力等于下滑力,此时的边坡处于临滑极限状态.这里主要讲述“毕肖普法”。

“毕肖普法”是在Fellenius法的基础上提出的一种简化方法，不同的是考虑了土条两侧的作用力和土条底部的反力M，并考虑了作用土条底部的孔隙水压μi，且定义安全系数为沿整个滑动面上的抗剪强度与实际产生的剪应力之比值，公式如下：F S=τf/τ=(c’+σtanø)/τ式中：τf为沿整个滑动面上的抗剪强度；Τ：实际产生的剪应力。

如图1所示，E i及X i分别表示法向及切向条间力，W i为土条自重，Q i为水平作用力，N i、T i分别为土条底部的总法向力(包括有效法向力及孔隙应力)和切向力。

土木工程中边坡稳定性分析方法在土木工程领域，边坡稳定性是一个至关重要的问题。

边坡的失稳可能会导致严重的人员伤亡和财产损失，因此，准确分析边坡的稳定性对于工程的安全和成功实施具有重要意义。

本文将探讨几种常见的土木工程中边坡稳定性分析方法。

一、定性分析方法1、工程地质类比法这是一种基于经验和对比的方法。

通过对已有的类似地质条件和边坡工程的研究和经验总结，来对新的边坡稳定性进行初步判断。

这种方法虽然简单快捷，但依赖于丰富的工程经验和大量的案例数据。

2、历史分析法通过研究边坡地区的历史地质活动、自然灾害记录以及以往的边坡变形破坏情况，来推断当前边坡的稳定性。

然而，这种方法受到历史资料完整性和准确性的限制。

二、定量分析方法1、极限平衡法这是目前应用较为广泛的一种方法。

它基于静力平衡原理，将边坡划分为若干个垂直条块，通过分析条块之间的力和力矩平衡，计算出边坡的安全系数。

常见的极限平衡法有瑞典条分法、毕肖普法等。

瑞典条分法假设滑动面为圆弧，不考虑条块间的作用力，计算较为简单，但结果相对保守。

毕肖普法考虑了条块间的水平作用力，计算结果更为精确，但计算过程相对复杂。

2、数值分析方法（1）有限元法将边坡离散为有限个单元，通过求解每个单元的应力和位移，来分析边坡的稳定性。

它可以考虑复杂的边界条件和材料非线性特性，能够更真实地模拟边坡的力学行为。

（2）有限差分法与有限元法类似，但采用差分格式来近似求解偏微分方程。

在处理大变形和复杂边界问题时具有一定的优势。

（3）离散元法特别适用于分析节理岩体等非连续介质的边坡稳定性。

它能够模拟块体之间的分离、滑动和碰撞等行为。

三、监测分析方法1、地表位移监测通过设置测量点，使用全站仪、GPS 等仪器定期测量边坡表面的位移变化。

当位移量超过一定的阈值时，提示边坡可能存在失稳风险。

2、深部变形监测采用钻孔倾斜仪、多点位移计等设备，监测边坡内部的深部变形情况。

这种方法能够更早地发现潜在的滑动面。

理正岩土计算理正岩土计算是指根据地质勘探资料和设计要求，通过一定的方法和公式来进行岩土工程的计算和分析，以确定工程的稳定性和安全性。

在进行岩土计算时，需要考虑到多方面的因素，如土的物理力学性质、岩土体的变形特性、地下水位等。

下面给出一些参考内容。

1. 岩土工程的基本原理：岩土工程是将土和岩体作为材料进行分析和计算的一门学科。

其中，土的物理力学性质和岩石的变形特性是岩土计算中最重要的两个方面。

土的物理力学性质包括土体的形变特性、抗剪强度、抗拉强度等，而岩石的变形特性主要包括岩石的压缩、剪切、弯曲等。

2. 岩土计算中的参数：在进行岩土计算时，常常需要通过试验或根据经验得到一些参数值，如土的密度、含水率、体积变形模量、剪切强度参数等。

这些参数值是岩土计算的基础，对于计算结果的准确性和可靠性具有重要意义。

3. 岩土计算的方法：岩土计算可以采用不同的方法和公式进行，其中最常用的方法包括极限平衡法、有限元法、变形体积法等。

极限平衡法是岩土计算中最常用的方法之一，其基本原理是通过假设土体和岩体处于临界平衡状态，通过平衡方程和强度准则来确定工程的稳定性。

4. 岩土计算的应用范围：岩土计算在岩土工程中的应用范围非常广泛，包括基础工程、地基处理、边坡工程、隧道工程等。

在进行岩土计算时，需要根据具体的工程要求和地质情况来选择适当的计算方法和参数值。

5. 岩土计算的案例分析：以某个具体的岩土工程为例，可以进行岩土计算的案例分析。

例如，在隧道工程中，需要通过岩土计算来确定隧道的稳定性和安全性。

这涉及到岩石的强度参数、地下水位、变形特性等多个因素，通过合理的计算方法和参数值，可以得到隧道的合理设计方案。

综上所述，岩土计算是岩土工程中非常重要的一部分，通过合理的方法和参数值，可以对岩土工程进行稳定性和安全性的评估。

在进行岩土计算时，需要综合考虑土的物理力学性质和岩石的变形特性，选择适当的计算方法和参数值。

岩土计算的应用范围广泛，涉及到基础工程、地基处理、边坡工程、隧道工程等多个领域。

有限元强度折减法综述及发展摘要：近年来，有限元强度折减法在工程上得到了广泛的应用，且取得了很大的成功。

这已经证明其在岩土工程上的可行性与优越性。

在边坡稳定性分析上的应用可以说是有限元强度折减法最为重要的应用之一，如今它在隧道工程上也得到了广泛应用。

有限元强度折减法最大的优点是可以运用大型有限元程序如ANSYS、ABQUS等来进行求解，并且不用事先假定滑移面的形式和位置就可得到边坡的稳定安全系数和破坏位置。

针对不同问题，要选择合适的屈服准则来进行求解，这样得到的计算结果与实际情况会更加接近。

在未来的发展过程中，有限元强度折减法的应用范围还将不断扩大，并且对于屈服准则的选取也会越来越精准。

关键词：有限元强度折减法; 屈服准则; 边坡稳定性分析; 隧道工程; 三维有限元强度折减法Summary and development of finite element strength reductionmethodDong Xiao-jiang(College of Sciences, xi’an University of Science and Technology, xi’an 710054, China)Abstract：In recent years, finite element strength reduction method has been widely used in the project and achieved great success，which has proved its feasibility and superiority in geotechnical engineering. The application in slope stability analysis can be said to be one of the most important applications of finite element strength reduction method. Now it has also been widely applied in Tunnel Engineering. The biggest advantage of finite element strength reduction method is that it can use some large finite element software like ANSY S、ABQU S to get solutions. Without assuming the modus and position of the slip plane we can get the safe factor and the destruction of the slope. Y ou should select the appropriate yield criterion to solve different problems. Only by that you can get closer result to the actual situation. In the future course of development, the scope of application of finite element strength reduction method will continue to be expanded and the selection of yield criterion will be more accurate.Key words: finite element strength reduction method; field criterion; slope stability analysis; tunnel engineering; three-dimensional finite element strength reduction method1、引言有限元强度折减法与有限元荷载增加法统称为有限元极限分析法,它们本质上都是采用数值分析手段求解极限状态的分析法。

求解边坡稳定安全系数两种方法的比较摘要：目前，边坡稳定性分析主要有刚体极限平衡法和有限元强度折减法，本文就理论基础、安全系数的定义及优缺点对以上两种方法进行了简要评述。

基于极限平衡法的发展起来的各种方法物理意义简单，便于计算，但是需要许多假设。

有限元强度折减法不需要假设，可以直接搜索临界滑动面并求出相应的安全系数，同时考虑了岩土体的弹塑性和边坡的破坏失稳过程。

通过对两种方法的认识比较，给岩土边坡工作者设计施工提供一定的参考价值。

关键词：边坡稳定性；极限平衡法；有限元法；安全系数引言边坡稳定分析是一个非常复杂的问题，从20世纪50年代以来，许多专家学者致力于这一研究，因此边坡稳定分析的内容十分丰富。

总体上来说，边坡稳定分析方法可分为两大类：定性分析方法和定量分析方法。

定性分析方法主要是通过工程地质勘探，可以综合考虑影响边坡稳定性的多种因素，对边坡岩土体的性质及演化史、影响边坡稳定性的主要因素、可能的变形破坏方式及失稳的力学机制等进行分析，从而给出边坡稳定性评价的定性说明和解释。

然而，人们更关心的是如何定量表示边坡的稳定性，即边坡稳定性分析的计算方法，定量方法将影响边坡稳定的各种因素都作为确定的量来考虑，通常以计算稳定安全系数为基础。

边坡稳定分析的定量方法有很多种，如条分法、数值分析方法、可靠度方法和模糊数学方法等[1-3]。

目前，边坡稳定分析方法中，人们较为熟知且广泛应用的有条分法和有限元方法。

条分法在边坡稳定分析中最早使用，因其力学模型概念清楚、简单实用，故广泛应用于实际工程中，已经逐渐成为边坡稳定分析的成熟方法。

随着计算机技术的发展，数值分析方法在工程领域应用越来越成熟，有限元方法考虑了土体的非线性应力－应变关系，同时弥补了条分法的不足，近年来有限元方法得到了极大的发展。

[4-6]刚体极限平衡法刚体极限平衡法是人们提出的最早的一类方法，是边坡分析的经典方法，只需要少许力学参数就能提供便于设计应用的稳定性指标即安全系数。

有限元强度折减法的原理、优点与超高边坡失稳的判据一、安全系数的定义两种方法可以导致边坡达到极限破坏状态，即：增量加载和折减强度。

传统边坡稳定分析中的安全系数是一个比值，假定一滑动面，根据力学的平衡来计算边坡安全系数，它等于滑动面以上土体条块的抗滑力与下滑力的比值。

式中K——安全系数；τ——滑动面上各点的实际强度。

将式子（4-1）两边同时除以k，上述公式变为其中：式（4-1）的左边等于I，表示滑坡体达到极限平衡状态，这意味着当代表强度的黏聚力和摩擦角被折减为1/K后，边坡最终到达破坏。

这个系数K就是有限元强度折减法中求解的安全系数，其实也就是强度折减系数。

二、有限元强度折减法的原理有限元强度折减法是在理想的弹塑性有限元计算中将边坡岩土体的抗剪强度参数：黏聚力c和内摩擦角φ按照安全系数的定义同时除以一个系数k，得到一组新的c′、φ′值，然后作为一组新的参数输入，再一次试算，如此循环。

当计算不收敛时，所对应的k被称为坡体的安全系数，此时边坡达到极限状态，将会发生剪切破坏，同时可以得到边坡的滑动面。

其中c′、φ′为三、有限元强度折减法的优点有限元强度折减分析法既具备了数值分析方法适应性广的优点，也具备了极限平衡法简单直观、实用性强的特点，目前被广大岩土工程师们广泛应用。

（1）不需要假定滑面的形状和位置，也无须进行条分。

只需要由程序自动计算出滑坡面与强度贮备安全系数。

（2）能够考虑“应力-应变”关系。

（3）具有数值分析法的各种优点，适应性强。

能够对各种岩土工程进行计算，不受工程的几何形状、边界条件等的约束。

（4）它考虑了土体的非线性弹塑性特点，并考虑了变形对应力的影响。

（5）能够考虑岩土体与支护结构的共同作用，并模拟施工过程和渐进破坏过程。

四、有限元强度折减法中超高边坡失稳的判据采用强度折减有限元方法分析超高边坡稳定性时，如何判断边坡是否达到极限平衡状态，十分关键。

这种有限元失稳判据的选取，没有获得共识，常见的失稳判据主要有下列三种。