基于有限元法和极限平衡法的边坡稳定性分析
- 格式:doc
- 大小:1.39 MB
- 文档页数:13

边坡稳定性分析方法及其应用综述引言:一、边坡稳定性分析方法1.隐式方法:隐式方法是边坡稳定性分析中常用的一种方法,它基于潜在平衡的假设,将边坡分析问题转化为求解非线性方程的问题。
其中最常用的方法为切线法、牛顿法和递归算法。
2.极限平衡方法:极限平衡方法是边坡稳定性分析中最常用的方法之一,它将边坡划分为滑动体和支撑体两个部分,通过平衡力的分析来确定边坡的稳定状态。
常用的方法有切片平衡法、切块平衡法和变形平衡法等。
3.数值模拟方法:数值模拟方法是近年来发展起来的一种边坡稳定性分析方法,它通过数值模拟地质体的力学行为来评估边坡的稳定性。
常见的方法有有限元法、有限差分法和边界元法等。
4.统计方法:统计方法是一种通过统计数据分析边坡稳定性的方法,它通过收集边坡历史数据来建立统计模型,然后预测未来边坡的稳定性。
常用的方法有回归分析、灰色系统理论和神经网络等。
二、边坡稳定性分析方法的应用1.土石坡的稳定性分析:土石坡是边坡稳定性分析的重要对象之一,它常见于土木工程和交通运输工程中。
通过对土石坡的稳定性进行分析,可以确定合适的边坡坡度和护坡措施,从而确保工程的安全和稳定。
2.岩质边坡的稳定性分析:岩质边坡是指由岩石构成的边坡,常见于水利工程和隧道工程中。
岩质边坡的稳定性分析需要考虑岩石的强度和岩体的结构特征,通过对岩质边坡的稳定性分析,可以确定合理的爆破参数和支护方式,从而确保工程的安全施工。
3.深部边坡的稳定性分析:深部边坡是指边坡的深度较大的边坡,常见于矿山工程和城市基础设施工程中。
深部边坡的稳定性分析需要考虑地应力、岩体的变形特性和地下水的影响等因素,通过对深部边坡的稳定性分析,可以确定合理的开采方式和支护措施,从而确保工程的安全运营。
4.风化边坡的稳定性分析:风化边坡是指由风化松散物质构成的边坡,常见于山区公路和铁路等工程中。
风化边坡的稳定性分析需要考虑土壤的强度和湿度等因素,通过对风化边坡的稳定性分析,可以确定合适的排水和防护措施,从而确保工程的安全与可靠。



降雨边坡的稳定计算
1. 极限平衡法:这是一种传统的边坡稳定分析方法,它基于静力平衡原理,考虑了土体的抗剪强度、重力、静水压力和外部荷载等因素。
在降雨条件下,可以通过计算不同降雨强度下的土体抗剪强度和静水压力,来评估边坡的稳定性。
2. 有限元法:这是一种数值计算方法,它将边坡划分为多个小单元,并通过求解每个单元的平衡方程来计算整个边坡的稳定性。
在降雨条件下,可以通过考虑不同降雨强度下的土体渗流和饱和度变化,来评估边坡的稳定性。
3. 概率分析法:这是一种基于概率统计的方法,它考虑了降雨的随机性和不确定性。
通过建立降雨强度和边坡稳定性之间的概率关系,可以评估不同降雨强度下边坡的稳定性。
4. 现场监测法:这是一种通过现场监测数据来评估边坡稳定性的方法。
在降雨条件下,可以通过监测边坡的位移、应变和地下水位等参数,来评估边坡的稳定性。
需要注意的是,以上方法都有其适用范围和局限性,需要根据具体情况选择合适的方法进行分析。
同时,在进行降雨边坡稳定计算时,还需要考虑土体的性质、边坡的几何形状、降雨的强度和持续时间等因素。

边坡稳定性分析方法及其适用条件边坡稳定性是指边坡在外力作用下保持不倒塌或滑动的能力,边坡稳定性分析方法一般可以分为经验法、力学方法和数值模拟方法三类。
不同方法适用于不同类型的边坡,且各方法在分析准确性、工程实施条件、运算速度以及数据要求等方面有所不同。
1.经验法:经验法是基于大量实际工程经验和观测总结出的简化计算方法,适用于边坡规模较小、地质条件比较简单的情况。
根据边坡的高度、坡度、土质等因素,通过经验公式计算出边坡的稳定性系数,从而判断边坡的稳定性。
2.力学方法:力学方法是通过岩土力学原理和边坡土体的力学性质来分析边坡稳定性。
力学方法主要应用于边坡高度较大、复杂地质条件的情况。
常用的力学方法包括平衡法、极限平衡法、有限元法等。
-平衡法:平衡法是基于边坡的平衡条件进行分析的方法,通过计算剪力平衡方程来确定边坡的稳定性。
平衡法适用于坡度较小、土体不饱和、坡面无裂缝等条件下的边坡稳定性分析。
-极限平衡法:极限平衡法是在平衡法的基础上引入抗剪参数的概念,通过计算抗剪参数的极限值来判断边坡的稳定性。
极限平衡法适用于任意坡度、土体饱和或部分饱和的边坡稳定性分析。
-有限元法:有限元法是一种基于连续介质力学和离散化原理的数值分析方法,将边坡土体划分成网格,通过求解有限元方程来计算边坡的应力和变形,并进而判断边坡的稳定性。
有限元法适用于复杂地质条件和复杂边坡形状的稳定性分析。
3.数值模拟方法:数值模拟方法是通过数值计算和模拟来分析边坡稳定性,主要利用计算机和专业软件进行模拟计算。
数值模拟方法通常适用于复杂地质条件、复杂边坡形状、非线性、动力等问题的研究。
常用的数值模拟方法包括有限差分法、边界元法、粒子法等。
总体来说,经验法适用于边坡规模较小、较简单的情况;力学方法适用于边坡规模较大、地质条件复杂的情况;数值模拟方法适用于复杂的边坡形状和非线性、动力问题。
在实际工程中,边坡稳定性分析通常采用多种方法相结合的方式,综合考虑不同方法的分析结果,从而提高分析的准确性。

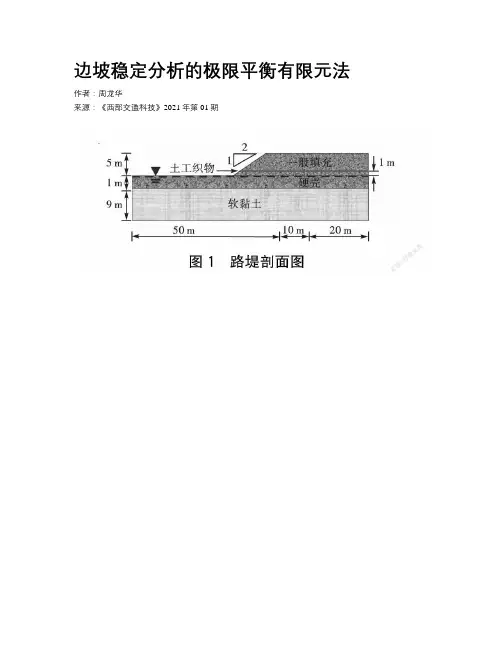
边坡稳定分析的极限平衡有限元法作者:***来源:《西部交通科技》2021年第01期摘要:极限平衡软件SLOPE/W和有限元程序PLAXE是目前岩土工程中常用的两种软件程序。
采用极限平衡法进行边坡分析时,需要将地面划分为若干垂直层面,并使用静态平衡方程计算各层面的安全系数(FOS)和应力,而有限元法则需要输入土的性质和单元的弹塑性参数。
文章比较了有限元法和极限平衡法在边坡稳定性分析中的应用,讨论了各种方法的适用性和局限性,并评估了边坡稳定性分析模型输出的实用性,可为边坡稳定性评估提供可靠依据。
关键词:有限元法;极限平衡;边坡稳定性中图分类号:U416.1+4文献标识码:ADOI:10.13282/ki.wccst.2021.01.022文章編号:1673-4874(2021)01-0078-030引言随着对基础设施和自然资源需求的不断扩大,对工程开挖和道路建设的要求也越来越高。
在工程建设过程中,山体滑坡和地震等自然灾害是岩土工程师和地质学家面临的重要问题。
边坡的稳定性是施工前、施工中、施工后各利益相关者共同关心的重要问题,如果要改变边坡稳定技术,安全系数(FOS)的微小差异可能导致施工成本的巨大差异。
这一点很重要,因为目前还没有明确的证据表明,哪种方法能产生最可接受的结果[1-3]。
与基础设施有关的土质边坡失稳是一个持续存在的问题,因为边坡破坏危及公共安全并导致昂贵的修复工作。
近几十年来,人们开发了一系列功能强大的边坡稳定分析设计软件包。
这些程序包括边坡稳定分析的极限平衡法和有限元法。
极限平衡法有许多局限性和不一致性,但被认为是最常用的方法。
随着技术进步,有限元程序简化了边坡稳定性分析。
SLOPE/W和PLAXIS是目前岩土工程师使用的两种常用软件程序。
SLOPE/W和PLAXIS分别用于极限平衡法和有限元法,每一个程序都被用来确定边坡的安全系数及其随后的设计要求。
根据所需的信息,分析和比较每个程序的结果将有助于确定哪个程序更准确。

常用的边坡稳定性分析方法边坡稳定性分析是土木工程中的一个重要内容,用于评估边坡的稳定性,并确定边坡设计和防护措施。
下面列举了常用的边坡稳定性分析方法:1.切片平衡法:切片平衡法是一种基本的边坡稳定性分析方法,它假设边坡由一系列无限小的土体切片组成,并基于力平衡原理来确定各个切片的稳定条件。
该方法适用于简单边坡稳定性分析,但对复杂地质条件和荷载情况适用性有限。
2.极限平衡法:极限平衡法是一种常用的边坡稳定性分析方法,它假设边坡存在一个明确定义的滑动面,并基于达到平衡的最不利情况,即极限平衡状态来进行分析。
该方法包括切片法、极限平衡法、回缩平衡法等,可以考虑复杂地质条件和荷载情况,适用范围广。
3.数值模拟方法:数值模拟方法是一种基于计算机模拟的边坡稳定性分析方法,包括有限元法、边界元法、离散元法等。
这些方法能够模拟边坡的实际行为,并对多种复杂因素进行定量分析。
数值模拟方法可以更精确地预测边坡的稳定性,并对工程设计提供参考。
4.基于概率的方法:基于概率的方法将不确定因素考虑在内,通过概率分析来评估边坡的稳定性。
这些方法包括可靠度法、蒙特卡洛方法和贝叶斯法等。
基于概率的方法可以提供边坡发生滑移的概率,并在风险评估和安全设计中发挥重要作用。
5.特殊情况下的分析方法:在一些特殊情况下,常规的边坡稳定性分析方法可能不适用,需要采用一些特殊的分析方法。
例如,在边坡潜在失稳或发生滑坡时,可以使用临界状态平衡、能量平衡或地震动力学方法来分析边坡的稳定性。
总之,边坡稳定性分析是土木工程中的重要任务,通过使用上述方法中的一个或多个,可以评估边坡稳定性,从而制定出合理的边坡设计和防护措施,确保工程的安全可靠。



基于极限平衡法及有限元法的边坡稳定性综合分析随着城市化进程的加快和土地资源的日益紧缺,地质灾害频繁发生成为了人们关注的焦点。
边坡稳定性分析作为地质灾害防治的重要内容之一,对于保障人民生命财产安全和城市发展具有重要意义。
本文将通过基于极限平衡法及有限元法的边坡稳定性综合分析,从两种不同的角度对边坡稳定性进行深入研究,以期为地质灾害防治提供理论支持和技术指导。
一、极限平衡法分析极限平衡法是指对于一定的边坡体系,在边坡体系受到外力作用时,通过平衡条件来确定边坡体系在达到稳定状态时,承受最大自重等荷载的状态。
具体步骤为:确定边坡的几何形状,计算边坡受力分布,确定边坡的抗滑稳定性和倾覆稳定性,得出边坡的稳定状态。
极限平衡法主要用于评估边坡在稳定状态下的安全系数,对于边坡的设计和监测具有重要意义。
二、有限元法分析有限元法是一种数值分析方法,将连续介质划分为有限个小单元,在每个小单元中建立方程,通过求解小单元之间的位移和应力关系来得出整个结构的位移和应力分布。
有限元法在地质灾害领域得到了广泛应用,能够较为准确地描述地质介质的力学行为,对复杂边坡体系的稳定性分析具有独特的优势。
基于有限元法的边坡稳定性分析首先要建立边坡的数值模型,将边坡体系划分为有限个小单元,然后确定边坡体系的边界条件和加载条件,进行有限元分析,计算得出边坡体系的位移和应力分布。
最后通过分析位移和应力的分布情况来评估边坡的稳定性。
三、综合分析将极限平衡法和有限元法两种分析方法相结合,可以更为全面地评估边坡的稳定性。
通过极限平衡法可以得到边坡在静态荷载下的稳定状态,而有限元法可以计算得出边坡在动态荷载下的位移和应力分布情况。
综合两种分析方法,可以较为全面地评估边坡的稳定性,为地质灾害防治提供更为可靠的技术支持。
基于极限平衡法及有限元法的边坡稳定性综合分析边坡稳定性的综合分析对于工程建设具有重要意义。
极限平衡法和有限元法是常用于边坡稳定性分析的两种方法。
本文将基于这两种方法,进行边坡稳定性的综合分析。
我们来介绍极限平衡法。
极限平衡法是边坡稳定性分析中常用的一种方法,其基本思想是在满足平衡条件的前提下,通过变换应力状态,找出使边坡发生稳定破坏的应力状态。
极限平衡法分析边坡稳定性的关键是确定初始滑动面,即通过分析土体的物理力学性质,选择一个合适的滑动面作为研究对象。
确定滑动面后,可以通过平衡条件,计算出边坡的抗滑力和抗倾覆力,进而判断边坡的稳定性。
在进行极限平衡法分析时,需要收集边坡所涉及的土体参数,如土体的黏聚力、内摩擦角等,这些参数可以通过室内实验或野外取样来获取。
还需要调查边坡所受的外荷载情况,如水压力、地震力等。
根据收集到的数据,可以通过相关的计算公式来计算边坡的稳定性指标,如安全系数等。
然后,我们来介绍有限元法。
有限元法是一种基于数值计算的方法,通过将边坡划分为离散的有限元单元,建立节点之间的联系,并在每个节点附近建立适当的求解方程,从而得到边坡的应力、应变和位移分布。
有限元法分析边坡稳定性的关键是选择合适的有限元单元,以及建立节点之间的边界条件和相应的求解方程。
通过求解这些方程,可以得到边坡的应力、应变和位移等信息,进而判断边坡的稳定性。
极限平衡法和有限元法是两种常用的边坡稳定性分析方法。
极限平衡法通过物理力学性质和平衡条件,计算边坡的抗滑力和抗倾覆力,进而判断边坡的稳定性。
而有限元法通过离散化边坡、建立节点之间的联系和求解方程,计算边坡的应力、应变和位移分布,进而判断边坡的稳定性。
这两种方法在边坡稳定性分析中有着各自的优势和适用范围,可以相互补充使用,提高边坡分析的准确性和可靠性。
基于极限平衡法及有限元法的边坡稳定性综合分析1. 引言1.1 研究背景边坡稳定性问题一直是土木工程领域中的热点难题,其解决既关系到人们的生命财产安全,也直接影响工程的质量和成本。
随着我国城市化进程的加快,大量的基础工程、水利工程、交通工程等都需要进行边坡设计与分析,而边坡稳定性是这些工程的关键问题之一。
当前,边坡稳定性分析方法主要有两种,即基于极限平衡法和基于有限元法。
极限平衡法是一种较为经典的边坡稳定性分析方法,它通过假设边坡体处于平衡状态,根据静力平衡和强度准则来评估边坡的稳定性。
而有限元法是一种基于数值模拟的方法,可以更为准确地考虑边坡体内部的应力和变形情况,但也需要较为复杂的计算和较高的计算资源。
本文将结合极限平衡法和有限元法,对边坡的稳定性进行综合分析。
通过比较两种方法的优缺点,确定在实际工程中的适用范围和条件,为工程设计提供科学依据。
本文还将通过案例分析和结果讨论,验证该方法的有效性,并对未来的研究方向做出展望。
1.2 研究意义边坡稳定性分析是岩土工程领域的重要研究课题,具有重要的理论和实践意义。
边坡稳定性分析可以帮助工程师评估和预测边坡的稳定性,有效地指导工程建设和维护工作。
在城市建设和交通基础设施建设中,边坡稳定性是保障工程安全的关键因素之一。
研究边坡稳定性不仅可以有效预防边坡滑坡和坍塌等灾害事故的发生,还可以提高工程的可靠性和持续性。
基于极限平衡法及有限元法的边坡稳定性综合分析,可以综合利用两种方法的优势,更加准确地评估和预测边坡的稳定性。
极限平衡法能够较为简便地确定边坡的稳定系数,而有限元法则可以更加精细地分析边坡的应力和变形特性。
结合两种方法,可以在较短的时间内得到较为可靠的边坡稳定性分析结果,为工程设计和施工提供重要参考。
对于边坡稳定性综合分析的研究具有重要的实际意义,将为岩土工程领域的发展和工程实践提供有力支持。
【研究意义】.1.3 国内外研究现状在边坡稳定性分析领域,国内外学者们进行了大量的研究工作,取得了一系列成果。
边坡稳定分析极限平衡法和有限元强度折减法对比研究发表时间:2019-12-16T15:34:32.643Z 来源:《防护工程》2019年16期作者:陈国良1 周人杰1 敖国辉2 罗书靖1 张弦1 [导读] 极限平衡法与有限元强度折减法是目前边坡稳定分析计算中常用的两种方法。
陈国良1 周人杰1 敖国辉2 罗书靖1 张弦1 1.中国电建集团华东勘测设计研究院浙江杭州 311122; 2.中国电建集团水电五局四川成都 610000摘要:极限平衡法与有限元强度折减法是目前边坡稳定分析计算中常用的两种方法。
本文以中东某混合坝边坡稳定计算为例,该混合坝基础内存在软弱夹层,采用极限平衡法与有限元强度折减法对边坡稳定性进行计算,总结分析了两种方法的计算结果及差异,并对分析方法进行探讨。
结果表明:极限平衡和有限元法法求解得到的安全系数较为接近,均可对含软弱夹层边坡进行模拟。
关键词:边坡稳定分析;极限平衡法;强度折减;软弱夹层 Title:Discussion on stability analysis method of the slope with weak intercalation//by CHEN Guo-liang, ZHOU Ren-jie,LUO Shu-jing and ZHANG Xian// PowerChina Huadong Engineering Corporation Limited Abstract:Limit equilibrium method and strength reduction FEM are two commonly used methods in slope stability analysis and calculation. In this paper,the slope stability calculation of a mixed dam in the Middle East is taken as an example,which has a weak intercalation in the foundation. The results show that the safety factors obtained by limit equilibrium method and strength reduction FEM are close to each other. The two methods all can be used in the weak intercalation simulation. Key words:Stability analysis of the slope;limit equilibrium method;strength reduction FEM;weak intercalation引言边坡稳定性问题是工程中普遍存在的地质灾害源,这些地质灾害分布范围广、容易灾发且破坏性强,岩土体一旦发生深层滑动,往往导致严重的生命和财产损失,边坡是否稳定与工程建设的安全与否与生产效益的高低有着密切的关系[1~3]。
目录摘要 (1)1引言 (1)2 简要介绍有限元和极限平衡方法 (1)3影响边坡稳定性的因素 (2)3.1水位下降速度的影响 (2)3.2 不排水粘性土对边坡失稳的影响 (5)3.3 裂缝位置的影响 (9)4 总结和结论 (12)基于有限元法和极限平衡法的边坡稳定性分析摘要:相较于有限元分析法,极限平衡法是一种常用的更为简单的边坡稳定性分析方法。
这两种方法都可用于分析均质和不均质的边坡,同时考虑了水位骤降,饱和粘土和存在张力裂缝的条件。
使用PLAXIS8.0(有限元法)和SAS-MCT4.0(极限平衡方法)进行了分析,并对两种方法获得的临界滑动面的安全系数和位置进行了比较。
关键词:边坡稳定;极限平衡法;有限元法;PLAXIS;SAS-MCT1.引言近年来,计算方法,软件设计和高速低耗硬件领域都得到快速发展,特别是相关的边坡稳定性分析的极限平衡法和有限元方法。
但是,使用极限平衡方法来分析边坡,可能会在定位临界滑动面(取决于地质)时出现几个计算困难和前后数值不一致,因此要建立一个安全系数。
尽管极限平衡法存在这些固有的局限性,但由于其简单,它仍然是最常用的方法。
然而,由于个人电脑变得更容易获得,有限元方法已越来越多地应用于边坡稳定性分析。
有限元法的优势之一是,不需要假设临界破坏面的形状或位置。
此外,该方法可以很容易地用于计算压力,位移,路堤空隙压力,渗水引起的故障,以及监测渐进破坏。
邓肯(1996年)介绍了一个综合观点,用极限平衡和有限元两种方法对边坡进行分析。
他比较了实地测量和有限元分析的结果,并且发现一种倾向,即计算变形大于实测变形。
Yu 等人(1998年)比较了极限平衡法和严格的上、下界限法对于简单土质边坡的稳定性分析的结果,同时,他们也将采用毕肖普法和利用塑性力学上、下限原理的界限法得到的结果进行了比较。
Kim等人(1999年)同时使用极限平衡法和极限分析法对边坡进行分析,发现对于均质土边坡,得自两种方法的结果大体是一致的,但是对于非均质土边坡还需要进行进一步分析工作。
Zaki(1999年)认为有限元相对于极限平衡法更显优势。
Lane和Griffiths (2000年) 提出一个看法,用有限元方法在水位骤降条件下评价边坡的稳定性,应绘制出适用于实际结构的操作图表。
Rocscience有限公司(2001年)提出了一个文件,概述了有限元分析方法的能力,并通过与各种极限平衡方法的结果比较,提出了有限元方法更为实用。
Kim等人(2002年)用上、下界限法和极限平衡法分析了几处非均质土体且几何不规则边坡的剖面。
这两种方法给出了类似有限元分析法产生的安全系数,临界滑动面位置。
2.简要介绍有限元和极限平衡方法有限元法(FEM)是一个应用于科学和工程中,求解微分方程和边值问题的数值方法。
进一步的细节,读者可参考Clough和Woodward(1967年),Strang和Fix(1973年),Hughes(1987年),Zienkiewicz和Taylor(1989年)所做的研究工作。
PLAXIS 8版(Brinkgreve 2002年)是一个有限元软件包,应用于岩土工程二维的变形和折稳定性分析。
该程序可以分析自然成型或人为制造的斜坡问题。
安全系数的确定使用ctan)和(c)依次降低直至结构发生破坏。
减的方法,土壤的强度参数(φ运用理想的塑性莫尔–库仑准则的极限平衡法(常规方法),多年来已广泛应用于岩土工程问题。
该方法是一个纯粹的静态数值分析技术,保持平衡质量取决于三个基本平衡方程。
自1866年Culmann第一次尝试处理数学与边坡稳定性问题以来,在这一领域已经进行了大量的研究(Yu等人,1998)。
通过使用各种垂直切片单元的方法,用来分析边坡的极限平衡法(LEM)已大大改进。
SAS-MCT第4版(Malkawi和Hassan,2003年)使用新开发的自动搜索程序,再加上新的蒙特卡洛法,通过随机跳跃和随机行走类型定位危险的圆形和非圆形滑动面(Malkawi等人,2000年,2001年)。
它是根据最常见的五种极限平衡方法确定的安全系数,即一般的或瑞典条分法(Fellenius,1936年),毕肖普简化法(Bishop,1955年),简布简化方法(Janbu,1973年),斯宾塞法(Spencer,1967年)和广义极限平衡法(GLE),离散的摩根斯坦-普瑞斯法(Morgenstern和Price,1965年)。
3.影响边坡稳定性的因素一般情况下,边坡稳定性分析中最重要的影响因素是:(1)边坡的几何形状;(2)土质;(3)作用在边坡上的力。
研究表明,三个不同例子在均质和非均质边坡应考虑到以下因素:(a)水位的下降速度;(b)粘土的不排水性;(c)裂缝的位置。
(a)此次研究将只集中研究水位的下降速度,因为这是一个关键性的问题。
当水的迅速抽离,将会降低水库边的边坡稳定性,因为没有足够的时间来稳定孔隙水压力。
(b)排水粘土边坡是一种特殊情况,因为土颗粒的摩擦剪应力强度通常较低。
快速加载细粒土将使水在空隙中消散。
对于饱和样品,内部摩擦角在该条件下将假定为零。
(c)张力裂缝的存在对于不稳定问题,在例子第一个幻灯片中是一个重要指标。
这些裂缝可能充满了水(例如,由于降雨)。
在抗拉强度低的粘性土中,他们变得很重要,尤其可以调动剪切强度以减少破坏面长度。
PLAXIS 8.0与SAS-MCT 4.0本文使用PLAXIS 8.0(有限元软件)和SAS-MCT 4.0(极限平衡法软件)研究分析了三个例子。
3.1水位下降速度的影响图1表示一个高度为10米,几何坡度为2:1(64°)均质简单边坡。
采用不同的比率Cγ)(0.10,0.15和0.20)和摩擦角(φ:12°,20°,30°和40°)来分析边坡。
Lane和Griffiths (HCγ)应该在0.01~1.0,摩擦角范围为12°~40°。
从0% (当水库已满,(2000年)认为,比率(H土壤完全饱和)到100%(当水库是空的,但土壤是完全饱和)分析了水位的迅速下降。
水位降低如图1所示,在最初的水位高度等于边坡(水位降低=0%)的高度,而在最后的的水位高度(Hw)是零(水位降低=100%)。
水位降低的百分比由Hw除以H×100所得。
图1 例1水位下降示意图图2指出在摩擦角为12,降低不同比率下的安全系数,水位的降低是一个普遍的趋势,Cγ)大小取决于选用何种方法,斯宾塞的方法的安全系数低于有限元。
水位降低但曲率(H的百分比越大,两种方法的安全系数几乎一样,这表明安全系数的值由水的重度控制。
斯宾塞法假设条间作用力与所有条单元的一样,与有限元法相比,斯宾塞法给出了较为保守的结Cγ(0.10,0.15和0.20)和摩擦角(12°,20°,30°和40°) 都能得到类似的结果。
在所有的H果。
安全系数的值由临界滑动面的形状决定,极限平衡法包含了滑动面横穿边坡和滑动面通过坡底,而有限元法的滑动面只通过坡底。
(如图3、4)图2 例1斯宾塞法和有限元法的比较(φ= 12°;C/γH = 0.1, 0.15, 0.2)图3 例1有限元的总位移轮廓图(C/γH = 0.15;φ= 30°).a. 水位降低= 20%;b. 水位降低= 80%图4 例1采用极限平衡法的非圆弧临界滑动面(C/γH = 0.15; φ= 30°) (a).水位降低 = 20%;(b).水位降低 = 80%3.2不排水粘性土对边坡失稳的影响此例子的边坡几何形状如图5所示,边坡高度为 6 m ,两个土层的容重为321/20m kN ==γγ,排水摩擦角为021==U U φφ。
所举的例子分析了不同比率的H C U γ/1值(0.15, 0.2, 0.25,和0.3)。
基础层的粘聚力2U C 的确定是为了计算不同比例的12/U U C C 的值(该值为0.5~3.0)和毕肖普法用于确定的极限平衡方法的安全系数,假设临界滑动面的形状是圆形。
图5 例2的边坡几何形状图6描述的是在比率H C U /1=0.2和不同12/U U C C 下所得的结果。
有限元分析显示了12/U U C C 从0.5到3.0的安全系数增加的趋势,而极限平衡法表明,当12/U U C C 增加到1.5后,安全系数趋于常数。
图6 例2采用不同的值比较有限元法和毕肖普法的结果(C u2/ C u1:C u1/γH=0.15,0.2,0.25)图7 例2采用不同的值比较有限元法和毕肖普法的结果(C u2=C u1和C u2≫C u1)当临界滑动面穿过基础层时,增加粘聚力会使该层的稳定性加强。
但如果临界面是在坡底,安全系数的值不会改变,因为顶层的粘聚力是固定值。
因此,安全系数由临界滑动面的位置决定。
由于有限元法提出了一个深滑动面(即基圆),安全系数提高了(图8)。
极限平衡法也提出了一个深滑动面,坡底破坏只发生在基础层的粘聚力是顶层粘聚力的1.5倍时(图9)。
一般情况下,两种方法所得的安全系数很相似(图7),但是当C U2大于C U1,边线角度更大时,有限元法比极限平衡法好。
同样,在用比率H C U /1进行分析时,这些结果也适用。
图8 例2有限元的总位移轮廓图(C u1/γH) = 0.25: a. (C u2/ C u1) = 1.0;b. (C u2/ C u1) = 1.5图9 例2采用极限平衡法的临界滑动面(Cu1/γH )= 0.25,a. (Cu2/ Cu1) = 1.0;b. (Cu2/ Cu1) = 1.53.3裂缝位置的影响例3的边坡几何形状如图10所示。
边坡由四种不同的土层组成,并有一水位线。
表1概述了土层的物理性质。
斯宾塞法和非圆弧滑动面用于极限平衡分析。
张力裂缝出现在陡坡后的不同位置(S = 5,10,15,20,25,30和35 m)。
张力裂缝深度为5 m。
图10 例3边坡几何形状和裂缝的位置表1 例3土层的物理属性土层摩擦角φ(°)粘聚力C(kN/m2)重度γ(kN/m3)1 32 20 18.22 30 25 18.03 18 40 18.54 28 40 18.8见图11,在使用极限平衡法分析时,安全系数随着陡坡水平距离的增加而增大。
而用有限元分析,安全系数基本保持在一条线上。
对于这种前后矛盾的主要原因是,有限元的滑动面在所有裂缝位置几乎相同(图12),而极限平衡法考虑到裂缝的位置随着破坏的进程而变化(图13)。
图11 例3中针对不同的裂缝位置比较有限元和简布法所得的结果图12 例3有限元的总位移轮廓图(a.S = 15 m;b. S = 25 m)图13 例3采用极限平衡法的非圆弧临界滑动面a.S = 15 m;b. S = 25 m表2 有限元法和极限平衡法所得安全系数的比较安全系数极限平衡方法安全系数的差异有限元法极限平衡法例1 (a)(b) 1.928 1.714 斯宾塞法12 1.505 1.369 斯宾塞法10例2 (a)(b) 1.464 1.472 毕肖普法 12.193 2.026 毕肖普法8例3(a)(b) 1.243 1.152 简布法8 1.241 1.218 简布法 24.总结和结论有限元法和极限平衡法都用于研究均质和非均质边坡的稳定性。