(仅供参考)自动控制理论实验报告-根轨迹仿真分析
- 格式:pdf
- 大小:1.58 MB
- 文档页数:12

实验二 控制系统的根轨迹1.实验目的1) 掌握MA TLAB 软件绘制根轨迹的方法。
2) 分析参数变化对根轨迹的影响。
3) 利用根轨迹法对控制系统性能进行分析。
2.实验仪器1) PC 机一台 2) MATLAB 软件 3.实验原理(1) 根轨迹的概念经典控制理论中,为了避开直接求解高阶特征方程式根时遇到的困难,提出了一种图解求根的方法,即根轨迹法。
根轨迹是指当系统的某个参数从零变化到无穷时,闭环特征方程的根在复平面上的变化曲线。
常规根轨迹一般取开环增益K 作为可变参数,根轨迹上的点应满足根轨迹方程:1)()()()(11*-=--=∏∏==ni imj jp s zs Ks H s G其中j z ---开环零点,i p ---开环极点,*K ---根轨迹增益,是一个变化的参数(∞→0),AK K =*,A 为一常数。
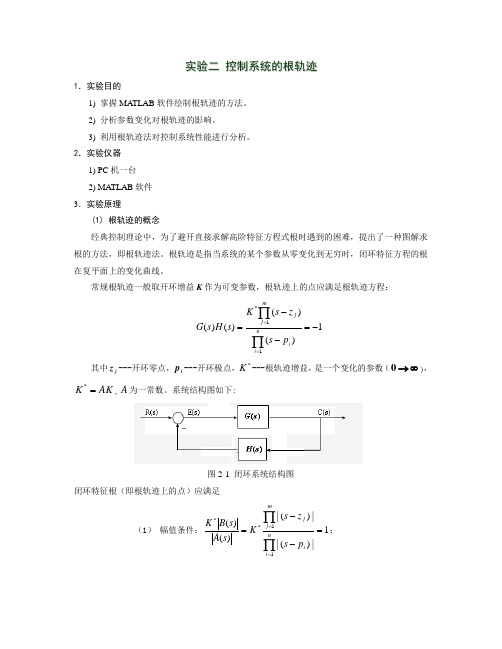
系统结构图如下:图2-1 闭环系统结构图闭环特征根(即根轨迹上的点)应满足(1) 幅值条件:1|)(||)(|)()(11**=--=∏∏==n i imj jp s zs K s A s B K ;(2) 相角条件:π)12()()(11+=-∠--∠∑∑==k p s zs ni i mj j。
(2)用MATLAB 软件绘制根轨迹MATLAB7.0提供的工具箱给出了一系列关于根轨迹的函数,如表2-1所示。
使用这些函数能够很方便地绘制出系统的常规根轨迹和参数根轨迹,还能基于根轨迹对系统性能进行分析。
表2-1 根轨迹函数① pzmap调用格式:pzmap(sys); [p,z]=pzmap(sys) ② rlocfind调用格式:[k,poles]=rlocfind(sys); [k,poles]=rlocfind(sys,p) ③ rlocus调用格式:rlocus(sys); rlocus(sys,k); [r,k]=rlocus(sys); r=rlocus(sys,k) ④ rltool调用格式:rltool(plant); rltool(plant,comp) ⑤ sgrid调用格式:sgrid; sgrid(z,wn) ⑥ zgrid调用格式:zgrid; zgrid(z,wn) 4.实验内容与步骤系统的开环传递函数:)2)(1()()(*++=s s s K s H s G绘制系统的根轨迹图。

实验四 控制系统的根轨迹分析一. 实验目的:1. 学习利用MATLAB 语言绘制控制系统根轨迹的方法。
2. 学习利用根轨迹分析系统的稳定性及动态特性。
二. 实验内容:1. 应用MATLAB 语句画出控制系统的根轨迹。
2. 求出系统稳定时,增益K 的范围。
3. 实验前利用图解法画出系统的根轨迹,算出系统稳定的增益范围,与实测值相比较。
4. 应用SIMULINK 仿真工具,建立闭环系统的实验方块图进行仿真。
观察不同增益下系统的阶跃响应,观察闭环极点全部为实数时响应曲线的形状;有共轭复数时响应曲线的形状。
(实验方法参考实验二)5. 分析系统开环零点和极点对系统稳定性的影响。
三. 实验原理:根轨迹分析法是由系统的开环传递函数的零极点分布情况画出系统闭环根轨迹,从而确定增益K 的稳定范围等参数。
假定某闭环系统的开环传递函数为)164)(1()1()()(2++-+=s s s s s K s H s G 利用MATLAB 的下列语句即可画出该系统的根轨迹。
b=[1 1]; %确定开环传递函数的分子系数向量a1=[l 0]; %确定开环传递函数的分母第一项的系数a2=[l -1]; %确定开环传递函数的分母第二项的系数a3=[l 4 16]; %确定开环传递函数的分母第三项的系数a=conv(al ,a2); %开环传递函数分母第一项和第二项乘积的系数 a=conv(a ,a3); %分母第一项、第二项和第三项乘积的系数 rlocus(b,a) %绘制根轨迹,如图(4-l )所示。
p=1.5i ; % p 为离根轨迹较近的虚轴上的一个点。
[k ,poles]=rlocfind(b ,a ,p) %求出根轨迹上离p 点很近的一个根及所对应的增益K 和其它三个根。
K=22.5031, poles= -1.5229+2.7454i -1.5229-2.7454i0.0229+1.5108i 0.0229-1.5108i再令p=1.5108i ,可得到下面结果:k=22.6464, poles=-1.5189+2.7382i -1.5189-2.7382i0.0189+1.5197i 0.0189-1.5197i再以此根的虚部为新的根,重复上述步骤,几步后可得到下面的结果: k=23.316, poles=-1.5000+2.7040i -1.5000-2.7040i0.0000+1.5616i 0.0000-1.5616i这就是根轨迹由右半平面穿过虚轴时的增益及四个根。

实验三,系统根轨迹分析实验报告实验三(1)10)()(SKsHsG根轨迹:K=1时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=10时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=100时;(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值(2))6)(2()()(SSKsHsG根轨迹:K=1时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=10时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=100时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值(3)2)3)(1()2()()(SSSKsHsG根轨迹:K=1时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=10时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=100时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值(4))5010)(2()3()()(2SSSSSKsHsG根轨迹:K=1时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=10时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=100时;(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值(5))5.2)(5.2()54)(5.1()()(22SSSSSSSKsHsG 根轨迹:K=1时;(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=10时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值K=100时:(1)分离点、会合点,根轨迹与虚轴交点(2)系统的零、极点的值。


自动控制原理根轨迹自动控制系统的根轨迹是描述系统稳定性和性能的重要工具之一。
根轨迹是以闭环传递函数的极点和零点的运动轨迹形状为基础绘制而成的。
在绘制根轨迹时,假设系统的闭环传递函数为G(s),其极点和零点分别为p1, p2, ..., pn和z1, z2, ..., zm。
根轨迹将从零点或者无穷远点开始,经过一系列的线段和曲线,最终到达极点或无穷远点。
根轨迹的演变与系统的开环传递函数有关,而开环传递函数可以表示为G(s) = K(s + z1)(s + z2)...(s + zm)/(s + p1)(s + p2)...(s + pn),其中K是系统的增益。
根轨迹的绘制规则如下:1. 根轨迹总是从系统的零点(实部为负的零点或倾角为奇数倍的复的零点)或者无穷远点开始。
2. 根轨迹图的总数等于系统的开环极点数和零点数之差。
3. 根轨迹的虚轴交点总数等于零点数和极点数之差的绝对值。
4. 根轨迹总是对称于实轴。
5. 根轨迹总是在实轴的左半平面。
通过绘制根轨迹,可以分析系统的稳定性和性能。
当根轨迹与虚轴相交时,系统就有可能发生震荡或振荡。
当根轨迹与实轴相交时,可以得到系统的过渡过程、稳态误差以及系统的稳定性等信息。
绘制根轨迹可以通过手绘或者使用计算机辅助工具进行。
一般来说,使用计算机辅助工具可以更加方便和准确地绘制根轨迹,并且可以对参数和增益进行调整来观察系统的性能变化。
常用的计算机辅助工具有MATLAB、Simulink等。
总之,根轨迹是描述自动控制系统稳定性和性能的重要工具,可以通过绘制闭环传递函数的极点和零点的运动轨迹来得到。
绘制根轨迹可以用于分析系统的震荡性质、过渡过程、稳定性和稳态误差等,并可以通过调整参数和增益来改善系统的性能。
编号:根轨迹仿真分析实验报告学生姓名专业班级学号日期自动控制理论根轨迹仿真分析实验报告一、实验目的1.学习和掌握根轨迹的原理及绘制方法;2.掌握开环零、极点在不同配置时,闭环根轨迹的变化特点及对系统动态性能的影响;3.掌握当增加开环零、极点时,闭环根轨迹的变化特点及对系统动态性能的影响;4.知道产生零度根轨迹的原因,了解参数根轨迹的绘制方法;5.了解运用计算机仿真绘制根轨迹的方法。
二、实验内容1.观察二极点一零点系统的根轨迹。
(1)指出该根轨迹的起始点与终止点,并说明它们与开环传函零、极点的关系;(2)指出根轨迹的分支数,在图上读出分离点坐标;(3)指出该类型根轨迹图形的特点,并在进一步实验中验证。
2.改变开环零极点位置对根轨迹的影响。
(1)给定一组Z ,p 1,p 2的值,绘出它的根轨迹;(2)取1'1p p =,2'2p p =,分别使Z Z >',Z Z <',绘出根轨迹,观察改变开环零点位置对系统性能的影响; (3)取Z Z =',改变'1p 、'2p 与p 1、p 2的大小关系,绘出根轨迹,观察改变开环极点位置对系统性能的影响。
3.改变零极点个数对根轨迹的影响。
(1)输入参数Z ,观察当增加一个开环零点时根轨迹的变化,零点位置变化对根轨迹的影响,对闭环系统的响应的影响;图2.1图2.2图2.3(2)输入参数P ,观察当增加一个开环极点时根轨迹的变化,极点位置变化对根轨迹的影响,对闭环系统的响应的影响;(3)观察同时引入开环极点和零点时,闭环根轨迹的变化和闭环系统的响应的变化;(4)观察引入重极点或者重零点时系统的根轨迹;(5)观察增加一对开环偶极子时系统根轨迹的变化,以及系统动态响应和稳态特性的变化;(6)观察当引入的开环零极点与原系统零极点对消时根轨迹的变化。
4.互逆系统的根轨迹。
()()()()()()()()()()()()32132323212211+++++=+++++=s s s s s s s H s G s s s s s s s H s G 观察如式(2-1)描述的互逆系统根轨迹的异同。
5.零度根轨迹。
观察根据图2.4系统所绘制的根轨迹与一般根轨迹的区别,判断导致零度根轨迹的原因。
观察根据图2.5系统所绘制的根轨迹,判断导致零度根轨迹的原因。
6.参数根轨迹。
绘制式(2-2)的根轨迹,并与计算机绘制图形比较。
011223=+++K s K s K s 其中K 1及K 2是可变参数,且其值都在0到∞之间。
7.绘制任意系统的根轨迹。
自由改变a 0、a 1、a 2、b 0、b 1、b 2、b 3和r 的值,观察绘制出的根轨迹图。
(2-1) (2-2)图2.4图2.5图2.6三、实验结果1.观察二极点一零点系统的根轨迹。
如图3.1所示,根轨迹始于开环极点()41.1 ,1-和()41.1 ,1-- ,终于开环零点()0 ,2-及无穷远处,有两条分支,分离点为()0 ,73.3-,为一段圆弧。
2.改变开环零极点位置对根轨迹的影响。
(1)使Z =2,p 1=3,p 2=4,则根轨迹如图3.2所示。
零点为()0 ,2-,极点为().321 ,5.1-和().321 ,5.1--,阶跃响应如图3.3所示。
图3.2 图3.3(2)使Z Z >=3',1'13p p ==,2'24p p ==,其根轨迹如图3.4所示。
零点为()0 ,3-,极点为().321 ,5.1-和().321 ,5.1--,阶跃响应如图3.5所示。
图3.1 图3.4 图3.5再使Z Z <=1',1'13p p ==,2'24p p ==,其根轨迹如图3.6所示。
零点为()0 ,1-,极点为().321 ,5.1-和().321 ,5.1--,阶跃响应如图3.7所示。
图3.6 图3.7 根据实验结果,可以说明增加开环零点可以改善系统的稳定性,且所增加的开环零点越接近坐标原点,微分作用越强,系统的相对稳定性越好(3)使Z Z ==2',1'14p p >=,2'25p p >=,其根轨迹如图3.8所示。
零点为()0 ,2-,极点为()2 ,2-和()2 ,2--,阶跃响应如图3.9所示。
图3.8 图3.9 再使Z Z ==2',1'12p p <=,2'22p p <=,其根轨迹如图3.10所示。
零点为()0 ,2-,极点为().411 ,1-和()41.1 ,1--,阶跃响应如图3.11所示。
图3.10 图3.11实验结果表明所增加的开环极点越接近原点,积分作用越强,超调量越大,系统的相对稳定性越差。
3.改变零极点个数对根轨迹的影响。
(1)先不改变零极点个数,其根轨迹如图3.12所示,阶跃响应如图3.13。
图3.12 图3.13若使a=1,b=0,Z=1,P=0,则其根轨迹如图3.14,零点为()0,1-,()0,2-,极点为()0,3-,(),1--,阶跃响应如图3.15。
.832-,().832,1图3.14 图3.15若使a=1,b=0,Z=3,P=0,则其根轨迹如图3.16,零点为()0,3-,()0,2-,极点为()0,3-,(),1-2-,阶跃响应如图3.17。
-,()2,1.83.83图3.16 图3.17以上结果表明,增加开环零点相当于增加微分环节,使根轨迹向左移动或弯曲,从而提高了系统的相对稳定性,并且使系统阻尼增加,过渡过程时间缩短。
零点越靠近原点,系统稳定性越好,但动态性能较差。
(2)若使a=0,b=1,Z=0,P=2,则其根轨迹如图3.18,零点为()0,2-,极点为()0,3-,(),1-2-,()0,2-,阶跃响应如图3.19。
.83.832,1-,()图3.18 图3.19若使a=0,b=1,Z=0,P=4,则其根轨迹如图3.20,零点为()0,2-,极点为()0,3-,(),1--,()0,4-,阶跃响应如图3.21。
2.832,1-,().83图3.20 图3.21上述实验结果表明,增加开环极点相当于增加积分环节,使根轨迹向右移动或弯曲,从而降低了系统的相对稳定性,并使系统阻尼减小,过渡过程时间加长。
增加的开环极点越接近坐标原点,积分作用越强,系统的相对稳定性越差。
(3)若使a=1,b=1,Z=1,P=4,即同时引入开环零点()0,1-和极点()0,4-,则其根轨迹如图3.22,阶跃响应如图3.23。
图3.22 图3.23结果表明,同时引入开环零点和极点对根轨迹的影响是:哪一个离原点更近,则哪一个对根轨迹的影响越大。
图3.22为零点距离原点较近,则根轨迹向左移,系统地相对稳定性增强。
(4)若引入重零点()0,1-,则其根轨迹如图 3.24所示,零点为()0,2-,图3.24()0 ,1-,()0 ,1-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--。
若引入重极点()0 ,1-,则其根轨迹如图3.25所示,零点为()0 ,2-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--,()0 ,1-,()0 ,1-。
(5)未增加开环偶极子时,其根轨迹如图3.26所示,零点为()0 ,2-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--。
若增加一对开环偶极子98++s s ,则其根轨迹如图3.27所示,零点为()0 ,2-,()0 ,8-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--,()0 ,9-。
图3.26 图3.27 以上结果表明,增加开环偶极子前后的根轨迹几乎没有差别,开环偶极子对系统动态性能和稳态性能的影响很小,几乎可以略去。
(6)若引入开环极点()0 ,2-与原系统零点对消,则其根轨迹如图3.28所示。
零点为()0 ,2-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--,()0 ,2-。
结果图3.25图3.28表明,引入开环极点()0 ,2-与原系统零点对消,则根轨迹向右移,系统的稳定性变差。
若引入开环零点()0 ,3-与原系统开环极点对消,则其根轨迹如图3.29所示。
零点为()0 ,2-,()0 ,3-,极点为()0 ,3-,().832 ,1-,()2.83 ,1--。
结果表明,引入开环零点()0 ,3-与原系统开环极点对消,则根轨迹向左移,系统稳定性增强。
4.互逆系统的根轨迹。
式(2-1)中,()()s H s G 11的根轨迹如图3.30所示,()()s H s G 22的根轨迹如图3.31所示,可以看出互逆系统的根轨迹图像除零极点位置交换外,图形无变化图3.30 图3.31 5.零度根轨迹。
图2.4所示系统根轨迹如图3.32所示,图2.5所示系统根轨迹如图3.33所示。
引起零度根轨迹具有两种情况:(1)非最小相位系统中包含s 最高次幂的系数为负的因子;(2)控制系统中包含有正反馈内回路。
由于在零度根轨迹绘制法则中,实轴上某一区域若右边开环实数零极点个数之和为偶数,则该区域必是根轨迹,故根轨迹图中在实轴上有某一点至正无穷为根轨迹时,该图为零度根轨迹。
图3.29图3.32 图3.33 6.参数根轨迹。
绘制式(2-2)的根轨迹。
以K 1为参量绘制根轨迹,传递函数为()()()()0 1231=+=K ss K s H s G 根轨迹如图3.34所示。
以K 2为参量绘制根轨迹,传递函数为()()11322K s K s s K s H s G ++= 根轨迹如图3.35所示。
图3.34 图3.35 7.绘制任意系统的根轨迹。
以《自动控制理论》(夏超英编著,科学出版社,2010)第161页习题4-3(c )为例绘制根轨迹。
4-3(c ) 设单位反馈控制系统的开环传递函数为()()()()325+++=s s s s K s G 试概略绘制出相应的K 从+∞→0变化时的闭环根轨迹。
如图3.36所示。
图3.36。