
第十一章习题答案
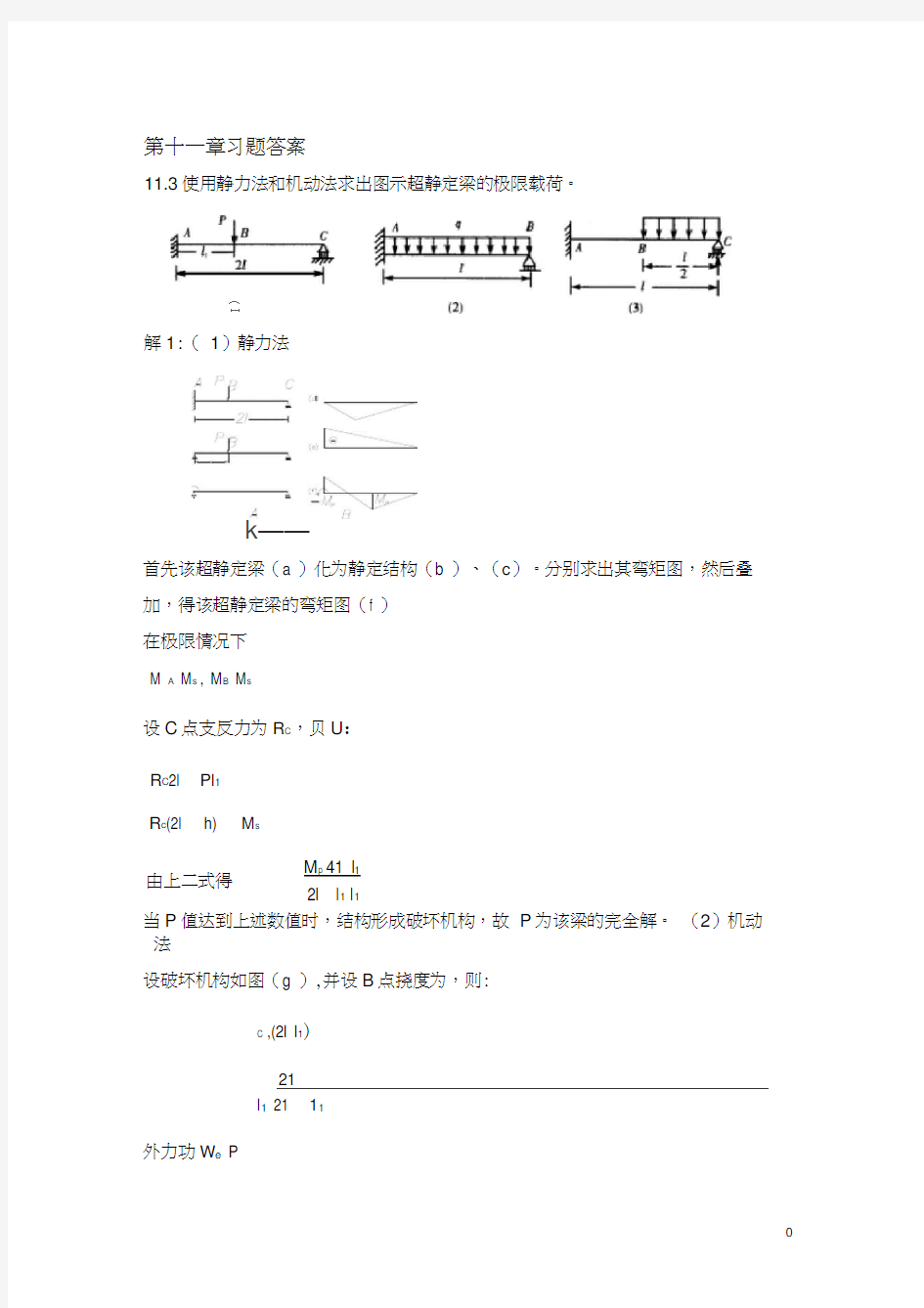
11.3使用静力法和机动法求出图示超静定梁的极限载荷。
解1:( 1)静力法
首先该超静定梁(a )化为静定结构(b )、(c )。分别求出其弯矩图,然后叠 加,得该超静定梁的弯矩图(f ) 在极限情况下
M A M s , M B M s
设C 点支反力为R C ,贝U :
R C 2l Pl 1
当P 值达到上述数值时,结构形成破坏机构,故 P 为该梁的完全解。 (2)机动法
设破坏机构如图(g ),并设B 点挠度为,则:
C
,(2l l 1)
21
l 1 21 11
外力功W e P
(I
R c (2l h) M s
由上二式得
M p 41 l 1 2l l 1 l 1
k ——
41 l
内力功 W i M AA M B B
—M l 1 21 l 1
由W e W ,可得极限载荷上限为
4l l
i l
i 2l l i
由于在P 作用下,M s M x M s ,故上式所示载荷为完全解的极限载荷。 解2:( 1)静力法
先将该超静定梁化为静定梁(b )、(c ),分别作弯矩图,叠加得该超静定梁的 弯矩图(f ) 设A 点为坐标原点,此时弯矩方程为: M x
R B l x
在极限状态时,有
M s
x x-1 ,M x 1 M s 令dM X
dx 0 得 q(l X i ) R B 而 R B l iql 2 1 2q (1)、(2)、(3)得 M s 2
l R B l X i 联立解
2qM s i i ql M s M s
(1) (2) (3)
解得q
ii2
i44 i6
M s l 2
在以上q0值作用下,梁已形成破坏机构,故其解为完全解
(2)机动法如图(g)
设在A、C两点形成塑性铰A B
内力功为
外力功为
由虚功原理W i W
该解与完全解的误差为
3%
q
解3:(1)静力法
设坐标原点在C点,此时弯矩方程为:
BC 段(0 x L 2)M (x) R c x qx2
1 1
AB段(L 2 x l)M (x)&X - ql x T
2 4
取较大的值,可得q011.66
处,M为极大值,设在BC段,由
dM x
dx
得R c q 0
R c
q
(1)
M s M s g2 3M s
l
W e 2 02q x dx 4q
得:q
12M s q0 11.66^
l2
b ----------- ----------------- H
在极限情况下
由于此时形成破坏机构,故q 值完全解 (2)机动法,如图(g )
设此梁在A 和处形成塑性铰,则
8(l
)
⑴ 四边简支,边长为a 的正方形板,载荷作用在板的中点;
(2) 三边简支一边自由的矩形板,在自由边中点承受集中力的作用;
(3) 四边简支矩形板,在板上任意点(x,y)承受集中力的作用.
M s
即:R c I 3 .2
8ql
M s
R c
1 2
2q M s
(2) (3)
q 188
取正号q
882 18 32 19.2
M s
A
..I , C
内力功为
W
M A
A
M
B B
M
C C
外力功为
W e
°
q
x dx
I 2
q
A B
I
I
— M s
由虚功原理 W i W 得
I(3I 4)M
s 由极值条件
dq
d
r 7 19 * 21
代入q 的表达式,则得
的极小值
q 11 47 M
s
由于此结果满足 M s
M I
M s
联立解(1)、(2)、(3)得
I x W o g dx
其中 —
4
3
代入上式后,得 W ; 8M s ctg ctg
w 0
4
3 8
16ctg M
s
内力功W i 2M s ctg ctg W
由W e W 得P 2M s ctg
ctg
而ctg
a ctg
2b
2b
a
故P 2M s ―
2b M s a 4
2b
a
b (b )外力功W e Pw 0
a
如破坏时四角可以翘起。内力功W i
8M s ctg ctg W o
由虚功原理W e W 得P 8M s ctg
ctg 3
4
其中值由产0确定即尙
? 2
3 sin
4
由此得
因此P 6.63M
(c)外力功W e Pw0
4
内力功W M s W0ctg i ctg i
i 1
ctg
1
y, x
,ctg 1
,ctg 2 a x,ctg 2y
其中x y y a x
b y a x x b y
ctg 3,ctg 3J ctg 4J ctg 4
a x
b y b y x
4
由W e W 得P M s ctg i ctg i
i 1
11.5使用机动法求图示连续梁的极限载荷。
解1:次梁为一次超静定梁,可能的破坏机构有两种,如图(b)、
(c)。
若塑性铰在B、D处形成,此时
外力功w e C 1 p g2g
内力功W i M s 2 M s 3M 由W e W i得P
若塑性铰在B、E处形
成, 设E到C得距离为x,此时有
M s
W E W o,
W o
B r_x
W o W o
E
外力功w e^qiW
。l _ 2
内力功W i M s W
o M s
由W e W i得P 2M s
0.41
1
l
x lx x l
—
Wo
x
—
Wo
x
将x 0.411代入P的表达式P “66牛
比较以上两种可知该梁的极限荷载为P 解
2:6 - l
该连续梁形成破坏机构有如下三种形式:
(1) 形成两个塑性铰产生局部破坏有两处可能,图(
W o l W o W o
2l l
3w o
2l
故w i
3w0
s
W
o
2l
5
2 W o
M s
l
由W e
图(c)E、F两点形成塑性铰,此时有W
o
2l
b)B、C形成塑性铰
w0w03w0
2l l 2l
故W i M s課W o
2l
2w o牛由W e W i得P
(2)形成三个塑性铰,产生局部破坏有三种可能:
比较上述六种情况,以(g )的情况P 为最小,而且此载荷满足 M s M M s 的
G j
:
A X
e
0.二
图(d )在B 、 D 、 E 三点形成塑性
铰,
此时有
3w 0 B 2l ,
D w o w 。
E l
W M s B
,
D E
9 M s w o
2 l
W e 2 Pw 0
由w e W 得P
9M s 4 l
图(e )在C 、 D 、F 三点形成塑性铰, 此时 W o C
-p ,
D
w °
2
「
w 。 F 叮
M s
W 6w 0 |
W e
Pw 0 P 2w 0 3Pw 0
由W e W 得P
M s 2 - l
图(f )在c 、
D 、
E 三点形成塑性
铰, 此时
W o C , D w
0 2「 w 。 E T
M s
W i 4w 0
|
W e
PW 。
由W e W 得P M s
4 -
1
(3)形成三个塑性铰,
产生整体破
坏,
只有一种可能性, 3w 0 B 2l , D w 。 2「 W o F 3T
13 M s
W w 0
2 l
W e Pw 0 Pw 0 P 2w 0 4Pw o
由w e W 得P 13M s
M s
1.625 s l
8 l
如图(g ),此时
塑性弯矩条件。 故破坏载荷为P 1.625叫
l
解3:该梁的可能破坏结构与第一题完全相同 若塑性铰在B 、D 处形成 12M
l
11.66
比较可知梁的极限载荷为P 11.66叫
I
解4:此梁为一次超静定结构,当形成两个塑性铰时,梁即成为破坏机构,其 破坏形式有(b ) ( c ) (d )三种可能。
1.33叫
I 比较得P 1.33业 I
11.6试求图示刚架的极限载荷.
若塑性铰在B 、 E 处形成
按图(b )形式破坏时
W o
B , D M s
W 3w 0 -p
2
W o
I
W e 2 PW 0
由W e W i 得P
按图(c ) c 3M s P s
I
按图(d )
W 。
E
U
M s
W 4w o -p
3叫
2 I
形式破坏时,同上得 形式破坏时 2
W o
I W e 3Pw 0
由W e W i 得P
解(a)设如图在ACDE四点形成塑性铰,
rj jr
i
i y
i
r
1
一-
由W e W得2P l P 2l M s M s 2 M
得P 1.5Ms
l
且此值满足M s M M s,条件
所以P 1.5Ms
l
解2:如图设在ACDE四点形成塑性铰,
由B点到C点的距离x待定
221 x x
由w e W得P 2
14P1x
2 2l 4M s 2M
化简得
4l x M s
2l x l x
令dP 0得dx
2 2
x 8lx 6l 0
故x 0.8381 P 1.48
业
l
解3:如图设在ACDEFG等处形成塑性铰。
外力功W e P 2l 2Pl 4Pl
故P 2.75叫
l
11.7简支圆板半径为R,受半径为轴对称均布载荷作用,试求其极限载荷.
解:圆板的平衡方程为
d rM r
—M rQ r
dr
当r 0 , M M r对应于Tresca条件的A点,当r R时,M r 0,M 0,对
x
2l x l
内力功W i M s M s 11M
由W e W得4Pl 11M
4M s M s
M
应于Tresca条件的B点,圆板r从0到R对应图上的AB线,即M 衡方程可写为
6M R a2 3R 2a M r,故平
d rM r
dr
M rQ r
a处,存在如下平衡关系: rQ r r
°q2rdr 0
1 2
2qr
平衡方程为
即rQ r
M
dr
积分上式得M r
M 1qr2 C1
由r 0处, M r,所以C l
因此有M r 1 2 6qr
在a r R处
a
2 rQ r q2 rdr
1
0 r 0 即rQ r
1
q
故此时区域的平衡方程为
M
dr
如2
积分上式得M r
在r a处连续条件, 可得C
2
r
1 2
6qa
C2
a
如C2 1qa3
因此有
1 2
M qa
2
a3
R时,M
a3
1qa2 昭―0
2 3 r
此式即为所求的极限载荷。
11.8对图所示的连续梁,利用上限定理求极限载荷
q.
题图11.6
解1 )对破损机构(a )
11.9图示宽度b 不变,高度h 线性变化的矩形截面梁,简支座截面高为h 。,固 I 1 1
定端处截面咼为4h °。集中力P 据简支端距离为l 1,对丄-,-两种情况用上限
I 3 5
1
x kl
虫
qkl 1
ql 1
2
2
2
x
R M s
1 2
M s l
x(l x)
可得q
2M s
(l x)(x k 2l)
由』 x
0, 得x
l 1 k 2
代入上式,得 2
2)对破损机构( b )
1
一 1
x
2
l x
R e 严R
2
由』 x
0, 得x 0.414l ,代入上式得,
q
8M s (a )
l 2 1 k 2
2
2M s 1 2
M s
1
2
2
q
l x l x
q 2M s 3
l 2 3 2.2
“657^ (b )
,故有
M s
1 k
2 2 l 2
k 2 l 2
(k 0.441)
当(a )式和(b )式相等时,k 0.441
(0 k 0.441)
题图11.7
解 由于各截面的M s 值不同,因此除集中力 作用点B 能形成铰外,另一铰C 距B 点距离 为12,而不一定总在固定端,如图所示。
2
3L i
2
3 k l 2
l
P
上式中x 是定值,调整y 使P 最小,由一0,得
y
方法求塑性极限载荷 M
sB
b% s
4 1
M
sC
bho s
4 1
2
) M sC 2,得
1 1
1
P
M S B
M sC —
l 1
l
2
l 2
令 l 1
x j,y
旦 l
,得
bh S
c
2
1 1
2
1
P
1 3x
—
—
1 3 x y
—
4l
x y
y
bh 2 S 12 1 27x 2
2
1
12x 18x 2 - 9y
4l
x
y
(a )
(b )
2
1
由外力功率P e
P ,内力功率P M sB ( 1
1
)
即x 1'代入(b)式,得y呼。因为x
1,而现在
2.2
3
1 ,故P最小值的y只能取在固定端处,将x I代入(a)式,
10.5 欝
2) 当11
l
1
-时,即
5
1
—,代入(b)式,得y
5
81。因为x
15 y 1,这表明铰
C不在固定端,将x 1,y整代入(a)
5 15
式,得P
8.994 bh
11.10用上限和下限方法求图示刚架的极限载荷P
解1 )上限法:
图示破损机构(a), (b), (c) , (d)都是
分别由外载荷引起的机构(a),
c 8M s
P -
l
机构(b),
C 8M S
P -
l
机构(c),
c 4M s
P s
l
机构(d),只上层刚架倾斜,点3 , 8 , 11 , 12成
C 8M S
P s l
对比之下,方案(c)对应的P值最小,为要进-步小
占
八
、
、
8, 10,11成铰
占
八
、
、
占
八
、
、
4,
1
,
5, 6成铰
4, 6, 9, 11, 12 成铰
(a)
(b)
(c)
(d)
个
铰
3.667 坐 I
这比机构(c )有了进一步改进, 是否最小的上限值还可用下限法作进一步检验 3)下限法:
从机构(e )出发,规定杆内表层受拉时弯矩为正,
时有 M j M s , M 2 M s , M 9 M s ,
M 4 M s ,M 6 M s ,M 10 M s ,M 12 M s ,
11 M
P ——-,未知的弯矩是M 3,M 5,M 7,M 8,Mn
3 I
列出平衡方程来求出这些未知弯矩。
11.11用静力法(即下限法)求图示刚架的极限载荷P ,要求把问题归结为标准 的线性规划问题,并用单纯形法求解。
P
值应减小内力功率,而增加外力功率所相应的速度项。 3 (e )中,R P —I ,与机构(c )时一样, 2
,而点4,10,12转角为.2,由此得出
在图示机构 10转角为 但P 较小,点1,6, 9, P 处 3l (e) 由结点A 的平衡,得M 3 M 2 M 4,得 M 3 o
由机构(b ),得平衡方程 M 4 2M 5 M 6 P
2
由机构(c )得平衡方程 11 得 M 5 M s M s
12 M 1 M 4 M 12 M 11 M 6 M 9
Pl
得Mu
M s
由机构(a ),得平衡方程
M 11 2M 10 M 8 P
得M 8
-M s 3 s
最后由结点 由于所有的 P 如
3l
i Ms M -,故所得的P 又是极限载荷的下限,因此
B 的平衡,得 M 7 0 得 M 7
M i 3
.667牛是极限载荷值。
题图11.9
解该钢架为二次超静定结构,可以列出两个独立的平衡方程,选用两种破 损机构作为虚位移,可由虚功原理求得两个平衡方程为 M 2 2M 3 M 4 2PI (a )
M , M 2 M 4 6PI
m 2 2m 3 mu 2q m ,
m 4 6q
这些截面的弯矩绝对值不允许超过 M s ,故有
1 m i
1
i 1,2,3,4 ( c )
n
标准的线性规划问题的提法为:求 X i (i 1,2,L ,n ),使f GX 取极小值
i 1
并满足下列约束条件:
n
d k
j 1
(k 1,2,L ,m)
(m n)
x i 0
(i 1,2,L , n)
d k 0
(k 1,2,L ,m)
现在要把满足方程(b ),(c )及使q 取最大值的问题化成标准的线性规划问
引进量纲为一的量m i
M i
M s ,q PI
M s'
则上式可表示成
(b )
题,这时可作下列变换:
(1)令x i m i 1 i 1丄,4可保证x i0 (2)令f q,把求q最大变成求f最小
(3) 增加变量X i 0(i 5,6,7,8),使不等式约束变成等式约
束。
(4) 在方程(b )中消去q 成为一个等式约束。 这样问题就变成如下标准的线性规划问题:
X i 0,
故是基本可行解,对应的f 0。
接着要进行换基,从最后一行看有哪些的系数是负的,现在只有一个系数 负的。因此X 3要进基,然后看这一列的系数,以这些系数为分母,右边的系数 为分子,第一行为-,第四行为-,其余的行分母为零不考虑,-的值为最小,
6 1 6 故取x i 出基,对第3列进行消去法,变成1, 0, 0, 0, 0, 0形式,结果如下表:
求 X i 0(i
1丄,8),
使f X2
~2 X 3 x-最小。 X i 4x 2 6X 3 2X 4
1
X 1 X 5
2
x - X 6 2
X 3 X 7 2
X 4 X 8
2
下面我们米用单纯形法求解,用列表方式进行。
X x - X 3 X 4 X 5
X 6 X 7 X 8 d 1
4 6
2 0 0 0 0 1 1 0 0 0 1 0
0 0 2 0 1 0 0 0 1 0 0 2 0 0 1 0 0 0 1 0 2 0 0
1 0
0 0 1 2 0 1
1 1 0 0
0 0 0
2 % 2
满足: 表中的值方程的系数,最后一行是 初始基本可行解:
取x 2 x 3 x 4 0,基本变量为x 1
f 的系数。 1,疋 1,X 6 2, X 7 2,x & 2。由于满足
X 1 X 2 X 3 X 4 冷 X 6 X 7 X d 1
2 1 1 0 0 0 0 1
6 3
3
6 1 0 0 0 1 0 0 0 2
0 1 0 0 0
1 0 0 2
1
2
1
11
0 0 1 0
6 3
3
~6
0 0 0 1 0
0 0 1 2
1
1
1
1
0 0 0
6
6 6
6
%
1
—,X 5 2, X 6
2, X 7 ?X 8 2,f -。已经 这时的解为 X 1 X 2 X 4 0,X 3
6 6 6
比初始基本解f 0有了进步,但最后一行系数还有负的,故尚需换基,现在X 2
要进基,由于第三行为2,1,第四行为爲I 3,因此X 3要出基,将第二亍消 成0, 0, 1, 0, 0, 0形式如卜表所示:
X X 2 X 3 X 4 X 5
X 6 X 7 X 8 d
1
1
2
3
0 1
0 0
6
3
3
2
1 0 0 0 1
0 0 0
2
0 1 0
0 0 1 0 0 2
1
1
2
1
0 0
1 0
6
3
3
2
0 0 0 1 0 0 0 1 2
1
1
1
1
0 0
0 0
6
6
6
2
这时对应的解为 X 1 X 4 X 0,x ? 2,X 3 3 c 1 ,X 5 2, X 7 , X 8 2, f
2,由于
2 2 2
最后一行系数都是正的,表示已求得线性规划问题的解,将结果恢复到原问题 则有
M 1 M
M i M s ,M 2 M s ,M 3 -,M 4 M s ,P -
2 2 l
这表示点1, 2,4成铰,对应的破损机构如图所示。
由于求线性规划问题的单纯形法已有成熟的计算机程序可以 利用,因此可以对复杂刚架用静力法求极限载荷问题,使用 单纯形法求解。
-厂
11.12长半轴为 件为
M M s
N N s
a ,短半轴为
b 的椭圆环,受力如图所示, 2
1,这里M s ,N s 分别表示纯弯时的极
假设环截面的屈服条 限弯矩
弹塑性力学简答题 第一章 应力 1、 什么是偏应力状态?什么是静水压力状态?举例说明? 静水压力状态时指微六面体的每个面只有正应力作用,偏应力状态是从应力状态中扣除静水压力后剩下的部分。 2、应力边界条件所描述的物理本质是什么? 物体边界点的平衡条件。 3、对照应力张量ij δ与偏应力张量ij S ,试问:两者之间的关系?两者主方向之间的关系? 相同。110220330 S S S σσσσσσ=+=+=+。 4、为什么定义物体内部应力状态的时候要采取在一点的领域取极限的方法? 不规则,内部受力不一样。 5、解释应力空间中为什么应力状态不能位于加载面之外? 保证位移单值连续。连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。 6、Pie 平面上的点所代表的应力状态有何特点? 该平面上任意一点的所代表值的应力状态1+2+3=0,为偏应力状态,且该平面上任一法线所代表的应力状态其应力解不唯一。 固体力学解答必须满足的三个条件是什么?可否忽略其中一个? 第二章 应变 1、从数学和物理的不同角度,阐述相容方程的意义。 从数学角度看,由于几何方程是6个,而待求的位移分量是3个,方程数目多于未知函数的数目,求解出的位移不单值。从物理角度看,物体各点可以想象成微小六面体,微单元体之间就会出现“裂缝”或者相互“嵌入”,即产生不连续。 2、两个材料不同、但几何形状、边界条件及体积力(且体积力为常数)等都完全相同的线弹性平面问题,它们的应力分布是否相同?为什么? 相同。应力分布受到平衡方程、变形协调方程及力边界条件,未涉及本构方程,与材料性质无关。 3、应力状态是否可以位于加载面外?为什么? 不可以。保证位移单值连续。连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。 4、给定单值连续的位移函数,通过几何方程可求出应变分量,问这些应变分量是否满足变形协调方程?为什么? 满足。根据几何方程求出各应变分量,则变形协调方程自然满足,因为变形协调方程本身是从几何方程中推导出来的。 5、应变协调方程的物理意义是什么? 对于单连通体,协调方程是保证由几何方程积分出单值连续的充分条件。多于多连通体,除满足协调方程方程外,还应补充保证切口处位移单值连续的附加条件。 6、已知物体内一组单值连续的位移,试问通过几何方程给出的应变一定满足变形协调方程吗?为什么?
弹塑性力学 第四章 弹性力学的基本方程与解法 一、线性弹性理论适定问题的基本方程和边界条件 对于在空间占有体积域V 的线弹性体在外加恒定载荷和固定几何约束条件下引起 的小变形问题,若以, , u εσ作为求解变量,则可以建立如下偏微分方程边值问题: 几何方程 ()1,,2ij i j j i u u ε= + ()12?+?u u ε= (1a) 广义胡克定律 ij ijkl kl E σε= :E σ=ε (1b) 平衡方程 ,0ij j i f σ+= ??+=f 0σ V ?∈x (1c) 以上方程均要求在域内各点均满足。 边界条件 u u i i = ?∈x S ui (2a) n t j ji i σ= ?∈x S ti (2b)对于适定问题,即不仅要求保证解存在唯一,而且有较好的稳定性。当载荷或边界条件给定值有微小摄动时,应能保证问题解的变化也是微小的。对于边界条件的提法就有严格的要求。即要求: S S S S S ui ti ui ti U I ==? (2c) 对于各向同性材料,其广义胡克定律可具体写成 σλεδεij kk ij ij G =+2 ()tr 2G λ+I σ=εε (3a) ()11ij ij kk ij E ενσνσδ??=+??? ()()1tr E νν=????I ε1+σ?σ (3b)以上就域内方程来说,一共是对于u ,,σ ε的15个独立分量u i ij ij ,, σε的15个方程。对于边界条件来说,三维问题每点有三个边界条件,而且是在三个正交方向上每个方向有一个边界条件,这个边界条件或者给定位移、或者给定面力。这三个正交
第二章 应力理论和应变理论 2—3.试求图示单元体斜截面上的σ30°和τ30°(应力单位为MPa )并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时,其符号及正负值 应作何修正。 解:在右图示单元体上建立xoy 坐标,则知 σx = -10 σy = -4 τxy = -2 (以上应力符号均按材力的规定) 代入材力有关公式得: 代入弹性力学的有关公式得: 己知 σx = -10 σy = -4 τxy = +2 由以上计算知,材力与弹力在计算某一斜截面上的应力时,所使用的公式是不同的,所得结果剪应力的正负值不同,但都反映了同一客观实事。 2—6. 悬挂的等直杆在自重W 作用下(如图所 示)。材料比重为γ弹性模量为 E ,横截面面积为A 。试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。 解:据题意选点如图所示坐标系xoz ,在距下端(原点)为z 处的c 点取一截面考虑下半段杆的平衡得: c 截面的内力:N z =γ·A ·z ; c 截面上的应力:z z N A z z A A γσγ??===?; 所以离下端为z 处的任意一点c 的线应变εz 为: z z z E E σγε==; 则距下端(原点)为z 的一段杆件在自重作用下,其伸长量为: ()2 2z z z z z z z z y z z l d l d d zd E E E γγ γε=???=??=? = ?= o o o o V ; 显然该杆件的总的伸长量为(也即下端面的位移): ()2 222l l A l l W l l d l E EA EA γγ?????=??= = = o V ;(W=γAl ) 2—9.己知物体内一点的应力张量为:σij =50030080030003008003001100-?? ??+-?? ??--?? 应力单位为kg /cm 2 。 试确定外法线为n i (也即三个方向余弦都相等)的微分斜截面上的总应力n P v 、正应力σn 及剪应力τn 。 解:首先求出该斜截面上全应力n P v 在x 、y 、z 三个方向的三个分量:n '=n x =n y =n z 题图1-3
第十一章 习题答案 11.3使用静力法和机动法求出图示超静定梁的极限载荷。 解1:(1)静力法 首先该超静定梁(a )化为静定结构(b )、(c )。分别求出其弯矩图,然后叠加,得该超静定梁的弯矩图(f ) 在极限情况下 ,A s B s M M M M =-= 设C 点支反力为C R ,则: 12C s R l Pl M -=- 1(2)C s R l l M -= 由上二式得() ()111 42p M l l P l l l * -= - 当P 值达到上述数值时,结构形成破坏机构,故P 为该梁的完全解。 (2)机动法 设破坏机构如图(g ),并设B 点挠度为δ,则: 11,(2)A C l l l θδθδ==- () 1122B A C l l l l δ θθθ=+= - 外力功e W P δ=
内力功() 1 1142i A A B B s l l W M M M l l l θθδ-=+= - 由e i W W =,可得极限载荷上限为 () 1 1142s l l P M l l l *-= - 由于在P *作用下,()s s M M x M -≤≤,故上式所示载荷为完全解的极限载荷。 解2:(1)静力法 先将该超静定梁化为静定梁(b )、(c ),分别作弯矩图,叠加得该超静定梁的弯矩图(f ) 设A 点为坐标原点,此时弯矩方程为: ()()()2 12 B M x R l x q l x =--- 在极限状态时,有 ()0,0s x M M ==- ()11,s x x M x M == 令 () 0dM x dx =得1()B q l x R -= (1) 而21 2 B s R l ql M -=- (2) ()()2 1112 B s R l x q l x M ---= (3) 联立解(1)、(2)、(3)得 2 1 22s s M qM ql l ??=- ??? 解得21122s M q l ?= ?
第七章 等截面柱体的弹塑性扭转 在船舶、航空、土建以及机械工程等的机械传动机构中,作为传递扭矩的柱体是个重要的部件。所谓柱体的扭转,是指圆柱体和棱柱体只在端部受到扭矩的作用,且扭矩矢量与柱体的轴线z 的方向相重合。 扭转问题属于仅在端面上受力柱体的平衡问题,若严格地满足其边界条件,按弹塑性力学求解是比较困难的。因此,利用圣维南原理,将边界条件放松,即认为柱体中间截面上的应力仅与端面上外力的合力及合力矩有关,这种放松了边界条件的问题称为圣维南问题。即使对于圣维南问题,仍需要求解一组偏微分方程,并使其满足一定的边界条件。但在实用上很少由直接积分其基本方程而得到解答,大部分工程问题用间接的或近似的方法得到。在间接方法中,圣维南的半逆解法是很重要的。即先在应力或位移分量中假设一部分未知函数,然后将这部分函数代入基本方程,求得另外一部分的未知函数,并使全部未知函数满足所给定的边界条件,则所假设的和求得的函数即为问题的解。由于用应力作为基本未知函数用半逆法求解时可以导致比较简单的边界条件,因此求解比较方便。 7.1 弹性柱体自由扭转的基本关系式与应力函数解 在材料力学中曾经过讨论圆轴的扭转,其特点是扭转变形前后的截面都是圆形,而且每一个截而只作刚体转动,在小变形条件下,没有铀向位移,取坐标系为z y x ,,,且柱体的轴线为z 方向,z 方向的位移为w ,即0),,(=z y x w 。这样,变形后截面的半径及圆轴长度基本不变。 非圆形截面柱体的情况要复杂得多。由于截面的非对称性,在扭转过程中,截面不再保持为平面,而发生了垂直于截面的翘曲变形,即0),,(≠z y x w 。函数 ),,(z y x w 称为翘曲函数。下面讨论任意截面形状的棱柱体扭转基本方程。 设有任意截面形状的等截面棱柱体,柱体两端受纠扭矩T M 作用,如图7.1所示。 1. 边界条件 对于扭转问题,柱体侧面为自由表面,因此柱体侧面的边界条件为 ?? ???=+=+=+000m l m l m l zy zx y xy xy x ττσττσ (7.1-1) 式中),cos(),,cos(n y m x n l ==。
第一章绪论 1.1弹塑性力学的任务 固体力学是研究固体材料及其构成的物体结构在外部干扰(载荷、温度交化等)下的力学响应的科学,按其研究对象区分为不同的学科分支。弹性力学和塑性力学是固体力学的两个重要分支。弹性力学是研究固体材料及由其构成的物体结构在弹性变形阶段的力学行为,包括在外部干扰下弹性物体的内力(应力)、变形(应变)和位移的分布,以及与之相关的原理、理论和方法;塑性力学则研究它们在塑性变形阶段的力学响应。大多数材料都同时具有弹性和塑性性质,当外载较小时,材料呈现为弹性的或基本上是弹性的;当载荷渐增时,材料将进入塑性变形阶段,即材料的行为呈现为塑性的。所谓弹性和塑性,只是材料力学性质的流变学分类法中两个典型性质或理想模型;同一种材料在不同条件下可以主要表现为弹性的或塑性的。因此,所谓弹性材料或弹性物体是指在—定条件下主要呈现弹性性态的材料或物体。塑性材料或塑性物体的含义与此相类。如上所述。大多数材料往往都同时具有弹性和塑性性质,特别是在塑性变形阶段,变形中既有可恢复的弹性变形,又有不可恢复的塑性变形,因此有时又称为弹塑性材料。本书主要介绍分析弹塑性材料和结构在外部干扰下力学响应的基本原理、理论和方法。以及相应的“破坏”准则或失效难则。 以弹性分析为基础的结构设计是假定材料为理想弹性,相应于这种设计观点就以分析结果的实际适用范作为设计的失效准则,即认为应力(严柞地说是应力的某一函数值)到达一定限值(弹性界限),将进入塑性变形阶段时、材料将破坏。结构中如果有一处或—部分材料“破坏”,则认为结构失效(丧失设计所规定的效用)。由于一般的结构都处于非均匀受力状态,当高应力点或高应力区的材料到达弹性界限时,类他的大部分材料仍处于弹性界限之内;而实际材料在应力超过弹性界限以后并不实际发生破坏,仍具有一定的继续承受应力(载荷)的能力,只 不过刚度相对地降低。因此弹性设计方法不能充分发挥材料的潜力,导致材料的某种浪费。实际上、当结构内的局部材料进入塑性变形阶段,在继续增加外载荷时,结构的内力(应力)分布规律与弹性阶段不同,即所谓内力(应力)重分布,这种重分布总的是使内力(应力)分布更趋均匀,使原来处于低应力区的材料承受更大的应力,从而更好地发挥材料的潜力,提高结构的承载能力。显然,以塑性分析为基础的设计比弹性设计更为优越。但是,塑性设计允许结构有更大约变形,以及完全卸载后结构将存在残余变形。因此,对于刚度要求较高及不允许出现残余变
弹塑性力学 弹塑性力学 绪论:弹性力学也称弹性理论,主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移,从而解决结构或机械设计中所提出的强度和刚度问题。在研究对象上,弹性力学同材料力学和结构力学之间有一定的分工。材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。 弹塑性力学是固体力学的一个重要分支,是研究弹性和塑形物体变形规律的一门学科。它推理严谨,计算结果准确,是分析和解决许多工程技术问题的基础和依据。在弹塑性力学中,我们可以看到很多学习材料力学、结构力学等学科所熟知的参数和变量,一些解题的思路也很类似,但是我们不能等同的将弹塑性力学看成材料力学或者是结构力学来学习。材料力学和结构力学的研究对象及问题,往往也是弹塑性力学所研究的对象及问题。但是,在材料力学和结构力学中主要采用简化的初等理论可以描述的数学模型;在弹塑性力学中,则将采用较精确的数学模型。有些工程问题(例如非圆形断面柱体的扭转、孔边应力集中、深梁应力分析等问题)用材料力学和结构力学的方法求解,而在弹塑性力学中是可以解决的;有些问题虽然用材料力学和结构力学的方法可以求解,但无法给出精确可靠的理论,而弹塑性力学则可以给出用初等理论所得结果可靠性与精确度的评价。在弹塑性力学分析中,常采用如下简化假设:连续性假设、均匀各向同性、小变形假设、无初应力假设等假设。 弹塑性力学基本方程的建立需要从几何学、运动学和物理学三方面来研究。在运动学方面,主要是建立物体的平衡条件,不仅物体整体要保持平衡,而且物体内的任何局部都要处于平衡状态。反映这一规律的数学方程有两类,即运动微分方程和载荷的边界条件。以上两类方程都与材料的力学性质无关,属于普适方
一、简答题 1答:(1)如图1所示,理想弹塑性力学模型: e s s e E E σε εεσεσεε=≤==>当当 (2)如图2所示,线性强化弹塑性力学模型: () 1e s s e E E σε εεσσεεεε=≤=+->当当 (3)如图3所示,幂强化力学模型:n A σε= (4)如图4所示,钢塑性力学模型:(a )理想钢塑性: s s εσσεσσ=≤=>当不确定 当 (b )线性强化钢塑性: ()0 /s s s E εσσεσσσσ=≤=->当当 图1理想弹塑性力学模型 图2线性强化弹塑性力学模型 图 3幂强化力学模型 (a ) (b ) 图4钢塑性力学模型 2答:
3答:根据德鲁克公设, ()00,0p p ij ij ij ij ij d d d σσεσε-≥≥。在应力空间中,可将0ij ij σσ-作为向量ij σ与向量0 ij σ之差。由于应力主轴与应变增量主轴是重合的,因此,在应力空间 中应变增量也看作是一个向量。利用向量点积的定义: ()0 0cos 0p p ij ij ij ij ij ij d σ σεσσε?-=-≥,?为两个向量的夹角。由于0ij ij σσ-和p ij ε都是 正值,要使上式成立,?必须为锐角,因此屈服面必须是凸的。 4 答:逆解法就是先假设物体内部的应力分布规律,然后分析它所对应的边界条件,以确定这样的应力分布规律是什么问题的解答。 半逆解法就是针对求解的问题,根据材料力学已知解或弹性体的边界形状和受力情况,假设部分应力为某种形式的函数,从而推断出应力函数,从而用方程和边界条件确定尚未求出的应力分量,或完全确定原来假设的尚未全部定下来的应力。如果能满足弹性力学的全部条件,则这个解就是正确的解答。否则需另外假定,重新求解。 二、计算题 1解:对于a 段有:0N a a a a F A E a a σσεε==?= ,对b 段有:0 N b b b b P F A E b b σσεε-==?= 又a b ?=? 则N bP F a b = + 2解:代入公式,116I =,227I =-,30I = 故117.5MPa σ=,20MPa σ=, 3 1.5MPa σ=- ()0123/3 5.33MPa σσσσ=++= 08.62MPa τ= = 3解:(1)代入公式,110I =,2200I =-,30I = 故主应力:120MPa σ=,20MPa σ=, 310MPa σ=-
弹塑性力学简答题
弹塑性力学简答题 第一章 应力 1、 什么是偏应力状态?什么是静水压力状态?举例说明? 静水压力状态时指微六面体的每个面只有正应力作用,偏应力状态是从应力状态中扣除静水压力后剩下的部分。 2、应力边界条件所描述的物理本质是什么? 物体边界点的平衡条件。 3、对照应力张量ij δ与偏应力张量ij S ,试问:两者之间的关系?两者主方向之间的关系? 相同。110220330 S S S σσσσσσ=+=+=+。 4、为什么定义物体内部应力状态的时候要采取在一点的领域取极限的方法? 不规则,内部受力不一样。 5、解释应力空间中为什么应力状态不能位于加载面之外? 保证位移单值连续。连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。 6、Pie 平面上的点所代表的应力状态有何特点? 该平面上任意一点的所代表值的应力状态1+2+3=0,为偏应力状态,且该平面上任一法线所代表的应力状态其应力解不唯一。 固体力学解答必须满足的三个条件是什么?可否忽略其中一个? 第二章 应变 1、从数学和物理的不同角度,阐述相容方程的意义。 从数学角度看,由于几何方程是6个,而待求的位移分量是3个,方程数目多于未知函数的数目,求解出的位移不单值。从物理角度看,物体各点可以想象成微小六面体,微单元体之间就会出现“裂缝”或者相互“嵌入”,即产生不连续。 2、两个材料不同、但几何形状、边界条件及体积力(且体积力为常数)等都完全相同的线弹性平面问题,它们的应力分布是否相同?为什么? 相同。应力分布受到平衡方程、变形协调方程及力边界条件,未涉及本构方程,与材料性质无关。 3、应力状态是否可以位于加载面外?为什么? 不可以。保证位移单值连续。连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。 4、给定单值连续的位移函数,通过几何方程可求出应变分量,问这些应变分量是否满足变形协调方程?为什么? 满足。根据几何方程求出各应变分量,则变形协调方程自然满足,因为变形协调方程本身是从几何方程中推导出来的。 5、应变协调方程的物理意义是什么? 对于单连通体,协调方程是保证由几何方程积分出单值连续的充分条件。多于多连通体,除满足协调方程方程外,还应补充保证切口处位移单值连续的附加条件。 6、已知物体内一组单值连续的位移,试问通过几何方程给出的应变一定满足变形协调方程吗?为什么?
应用弹塑性力学习题解答 目录 第二章习题答案 (2) 第三章习题答案 (6) 第四章习题答案 (9) 第五章习题答案 (26) 第六章习题答案 (37) 第七章习题答案 (49) 第八章习题答案 (54) 第九章习题答案 (57) 第十章习题答案 (59) 第十一章习题答案 (62)
第二章习题答案 2.6设某点应力张量的分量值已知,求作用在过此点平面上的应力矢量,并求该应力矢量的法向分量。 解该平面的法线方向的方向余弦为 而应力矢量的三个分量满足关系 而法向分量满足关系最后结果为 2.7利用上题结果求应力分量为时,过平面处的应力矢量,及该矢量的法向分量及切向分量。 解求出后,可求出及,再利用关系 可求得。 最终的结果为
2.8已知应力分量为,其特征方程为三次多项式,求。如设法作变换,把该方程变为形式,求以及与的关系。 解求主方向的应力特征方程为 式中:是三个应力不变量,并有公式 代入已知量得 为了使方程变为形式,可令代入,正好项被抵消,并可得关系 代入数据得,, 2.9已知应力分量中,求三个主应力。 解在时容易求得三个应力不变量为, ,特征方程变为 求出三个根,如记,则三个主应力为 记
2.10已知应力分量 ,是材料的屈服极限,求及主应力。 解先求平均应力,再求应力偏张量,, ,,,。由此求得 然后求得,,解出 然后按大小次序排列得到 ,, 2.11已知应力分量中,求三个主应力,以及每个主应力所对应的方向余弦。 解特征方程为记,则其解为,,。对应于的方向余弦,,应满足下列关系 (a) (b) (c) 由(a),(b)式,得,,代入(c)式,得 ,由此求得
R r u A A' x y z Ch3-1 位移与应变几何方程 分量形式: 符号规定:与坐标轴同向为正 刚体位移:各点间相对位置在物体发生位移后依然不变。 刚体位移不会使物体产生变形 n 位移: 定义A 点位移: u =r -R 位移—物体内每一点的空间位置的变化位移场:物体内各点位移矢量的集合 l l l ?′= εα ?=γ0 90A B A B l l ' ' ' x y z A B A B l l ''' C C ' α 90 x y z o 应变:符号规定:正应变—线元伸长为正 剪应变—直角变小为正 物体变形 { 体积改变形状畸变 长度变化,方向改变 O A B C O A B C ' ' ' 'x y z OA OA -A O x ′′= ε OB OB -B O y ′′= ε OC OC -C O z ′′= εA O B yx xy ′ ′′∠?π =γ=γ2B O C zy yz ′ ′′∠?π =γ=γ2C O A zx xz ′ ′′∠?π =γ=γ2 与一点的应力状态相似,可以证明:应变张量决定了一点的应变状态
x u dx u dx x u u x ??= ??? ??????+=εy v dy v dy y v v y ??= ???????????+=εx v dx v dx x v v yx ??= ???+= α)(y u dy u dy y u u xy ??= ???+= α)(xy u v y x γ??= +??dx x u u ??+dx x v v ??+dy y u u ??+dy y v v ??+考虑小变形假定 v αxy αyx x y O A B A'B' O' u x u x ε?= ?y v y ε?= ?xy yx u v y x γγ??== +??z w z ??= εyz zy v w z y γγ??== +??xz zx u w z x γγ??== +??几何方程(小变形): 其他应变分量同理可以得出 z w z ??= εx w z u zx xz ??+??= γ=γy w z v zy yz ??+??= γ=γε εεεε εεεε ε???? =?? ????? ? 1 2ij ij εγ=几何方程张量表示 )(2 1 ,,i j j i ij u u += εCauchy 应变 张量 ??? ???????????? ???+=dx x w dx x v dx x u A'M',, 1??? ???????????????+??=dy y w dy y v dy y u B'M',,1? ??????????? ??+????=dz z w dz z v dz z u C'M'1,,Ch3-2 体积应变 M 点位移,,) u v w (A B C A B C ' ' ' x y z M M ' d z d x d y 变形后各边长沿坐标轴的投影
3. STRAIN 3.1. Deformation and Strain tensor In present chapter we examine the deformation geometry of the deformable solid without regard for the actual forces required to produce it. The most obvious and direct method of describing the motion of a continuum solid is to consider the motion of each and every particle making up the solid. If the relative position of every particle is not changed, there is only rigid moving and rotation, then we may consider it as a rigid displacement. If the relative position of every particle is changed, in the same time the initial shape of the body is distorted, then we called there is a deformation. In the following, we will discuss the deformation of elastic-plastic body. Suppose the distance between two points P o(x o, y o) and P(x,y) is P o P in plane Oxy before deformation. After deformation the two ends of segment P o P moved to P o′(x o′y o′) and P′(x′, y′). Let P o P =s, P o′P′= s ′then the components of vectors s′and s along the x , y axes are: s x′=s x+ s x s y′=s y′+s y The displacement component at point P o is u o =x o′?x o v o =y o′?y o (3.1) Similarly, at point P the displacement component is(Fig.3.1): u =x′– x v =y′– y (3.2) Suppose the displacement u and v are the single-value continuously functions of x and y, then we can expand the displacement at point P in an infinite Taylor series about point P o, that is: u = u o + s x + s y + 0 (s x2, s y2 ) v =v o + s x + s y+ 0(s x2, s y2) (3.3) Because point P is in the neighbourhood of the point P o, therefore the quantity s is sufficiently small, so that we obtain the formula s x =s x′–s x = (x′-x ) – (x o′-x o ) = s x+s y s y =s y′–s y = (y′-y) – (y o′-y o )= s x+ Using the indicial notation and summation convention, these equations
第三章 应变状态理论 在外力、温度变化或其他因素作用下,物体内部各质点将产生位置的变化, 即发生位移。如果物体内各点发生位移后仍保持各质点间初始状态的相对位置,则物体实际上只发生了刚体平移和转动,这种位移称为刚体位移。如果物体各质点发生位移后改变了各点间初始状态的相对位置,则物体同时也产生了形状的变化,其中包括体积改变和形状畸变,物体的这种变化称为物体的变形运动或简称为变形,它包括微元体的纯变形和整体运动。应变状态理论就是研究物变形后的几何特性。即给定物体内各点变形前后的位置,确定无限接近的任意两点之间所连矢量因物体变形所引起剧烈变化。这是一个单纯的几何问题,并不涉及物体变形的原因,也就是说并不涉及物体抵抗变形的物理规律。本章主要从物体变形前后的几何变化论述物体内一点的应变状态。 位移与线元长度、方向的变化 坐标与位移 设变形前物体上各点的位置在笛卡尔坐标(Descarter coordinate)系的轴(X 、、Y、Z )上的投影为(z y x ,,),又设物体上各点得到一位移,并在同一坐标轴上的投影为(u 、v 、w ),这些位移分量可看作是坐标(z y x ,,)的函数。于是物体上任点的最终位置由下述坐标值决定。即 ?? ? ?? +=+=+=),,(),,(),,(z y x w z z y x v y z y x u x ζηξ 上式中函数u 、v 、w 以及它们对坐标(z y x ,,)的偏导数假设是连续的,则式确定了变量(z y x ,,)与),,(ζηξ之间的关系。因为物体中变形前各点对应看变形后的各点,因此式是单值的,所以式可看成是坐标的一个变换。 如果在中,假设00,y y x x ==,则由式可得如下三个方程
第十一章习题答案 11.3使用静力法和机动法求出图示超静定梁的极限载荷。 解1:( 1)静力法 首先该超静定梁(a )化为静定结构(b )、(c )。分别求出其弯矩图,然后叠 加,得该超静定梁的弯矩图(f ) 在极限情况下 M A M s , M B M s 设C 点支反力为R C ,贝U : R C 2l Pl 1 当P 值达到上述数值时,结构形成破坏机构,故 P 为该梁的完全解。 (2)机动法 设破坏机构如图(g ),并设B 点挠度为,则: C ,(2l l 1) 21 l 1 21 11 外力功W e P (I R c (2l h) M s 由上二式得 M p 41 l 1 2l l 1 l 1 k ——
41 l 内力功 W i M AA M B B —M l 1 21 l 1 由W e W ,可得极限载荷上限为 4l l i l i 2l l i 由于在P 作用下,M s M x M s ,故上式所示载荷为完全解的极限载荷。 解2:( 1)静力法 先将该超静定梁化为静定梁(b )、(c ),分别作弯矩图,叠加得该超静定梁的 弯矩图(f ) 设A 点为坐标原点,此时弯矩方程为: M x R B l x 在极限状态时,有 M s x x-1 ,M x 1 M s 令dM X dx 0 得 q(l X i ) R B 而 R B l iql 2 1 2q (1)、(2)、(3)得 M s 2 l R B l X i 联立解 2qM s i i ql M s M s (1) (2) (3) 解得q ii2 i44 i6 M s l 2
在以上q0值作用下,梁已形成破坏机构,故其解为完全解 (2)机动法如图(g) 设在A、C两点形成塑性铰A B 内力功为 外力功为 由虚功原理W i W 该解与完全解的误差为 3% q 解3:(1)静力法 设坐标原点在C点,此时弯矩方程为: BC 段(0 x L 2)M (x) R c x qx2 1 1 AB段(L 2 x l)M (x)&X - ql x T 2 4 取较大的值,可得q011.66 处,M为极大值,设在BC段,由 dM x dx 得R c q 0 R c q (1) M s M s g2 3M s l W e 2 02q x dx 4q 得:q 12M s q0 11.66^ l2 b ----------- ----------------- H
附录Ⅱ习题解答提示与参考答案 第二章应力理论 2-1 ζn=ζ1l2+ζ2m2,;式中l、m、n为斜截面外法线的方向余弦。 2-2 p=111.5A;ζn=26A;ηn=108.5A 2-3 提示:平面Ax+By+C z+D=0的外法线的方向余弦为:(式中i=1,2,3或A,B,C) 答案: 2-4 略 2-5 (a)ζ1=738.5;ζ2=600;ζ3=-338.5;ηmax=538.5;应力单位为MPa。 (b)ζ1=700;ζ2=600;ζ3=-600;ηmax=650;应力单位为MPa。 2-6 ζ1=3.732η0;ζ2=-0.268η0;α=15o。 2-7 (材料力学解) 应力单位为MPa。 (弹塑性力学解) 应力单位为MPa。 2-8 ζ1=107.3a;ζ2=44.1a;ζ3=-91.4a; ζ1主方向:(±0.314,0.900,0.305); ζ2主方向:(±0.948,±0.282,±0.146); ζ3主方向:(0.048,±0.337,0.940)。 2-9 ;ζ2=0;ζ3=-ζ1。 2-10、2-11 略 2-12 (1)略;(2)ζ8=ζm=5.333MPa;η8=8.654MPa。 2-13 p8=59.5;ζ8=25.0a;η8=54.1a。 2-14 上式中S为静矩。材料力学解不满足平衡微分方程和边界条件。
2-15 ,Q为梁横截面上的剪力。提示:利用平衡微分方程求解。2-16 ζ1=17.083×103Pa;ζ2=4.917×103Pa;ζ3=0,?=40o16′。2-17 略2-18 2。2-19 提示:将三个主方向的三组方向余弦分别两两一组代人式(2-12)证之。2-20 。2-21 在AA′上:ζx=-γy,ηxy=0;在AB上:ηxy=0,ζy=-γh;在BB′上:l1=cosα,l2=-sinα,l3=0;则应力分量满足关系式:2-22 。2-23 。2-24 ηzx=-ζz tanα;ζx=ζz tan2α。2-25 在x=-ytanα处,在x=ytanβ处: 2-26 A=0;B=-ρ1g;C=ρgcotβ-2ρ1gcot3β;。 2-27 (1)ζ1=99.6A;ζ2=58.6A;ζ3=-138.2A;ηmax=118.9A。 (2)ζ1=99.6A;ζ2=58.6A;ζ3=-138.2A;ηmax=118.9A。
弹塑性力学简答题 第一章应力 1、什么是偏应力状态?什么是静水压力状态?举例说明? 静水压力状态时指微六面体的每个面只有正应力作用,偏应力状态是从应力状态中扣除静水压力后剩下的部分。 2、应力边界条件所描述的物理本质是什么? 物体边界点的平衡条件。 3、对照应力张量 ij 与偏应力张量ij S,试问:两者之间的关系?两者主方向之间的关系? 相同。110 220 330 S S S 。 4、为什么定义物体内部应力状态的时候要采取在一点的领域取极限的方法? 不规则,内部受力不一样。 5、解释应力空间中为什么应力状态不能位于加载面之外? 保证位移单值连续。连续体的形变分量 x 、y、xy不是互相独立的,而是相关,否则导致位移不单值,不连续。 6、Pie平面上的点所代表的应力状态有何特点? 该平面上任意一点的所代表值的应力状态1+2+3=0,为偏应力状态,且该平面上任一法线所代表的应力状态其应力解不唯一。 固体力学解答必须满足的三个条件是什么?可否忽略其中一个? 第二章应变 1、从数学和物理的不同角度,阐述相容方程的意义。 从数学角度看,由于几何方程是6个,而待求的位移分量是3个,方程数目多于未知函数的数目,求解出的位移不单值。从物理角度看,物体各点可以想象成微小六面体,微单元体之间就会出现“裂缝”或者相 互“嵌入”,即产生不连续。 2、两个材料不同、但几何形状、边界条件及体积力(且体积力为常数)等都完全相同的线弹性平面问题, 它们的应力分布是否相同?为什么? 相同。应力分布受到平衡方程、变形协调方程及力边界条件,未涉及本构方程,与材料性质无关。 3、应力状态是否可以位于加载面外?为什么? 不可以。保证位移单值连续。连续体的形变分量 x 、y、xy不是互相独立的,而是相关,否则导致位移不单值,不连续。 4、给定单值连续的位移函数,通过几何方程可求出应变分量,问这些应变分量是否满足变形协调方程? 为什么? 满足。根据几何方程求出各应变分量,则变形协调方程自然满足,因为变形协调方程本身是从几何方程中 推导出来的。 5、应变协调方程的物理意义是什么? 对于单连通体,协调方程是保证由几何方程积分出单值连续的充分条件。多于多连通体,除满足协调方程 方程外,还应补充保证切口处位移单值连续的附加条件。 6、已知物体内一组单值连续的位移,试问通过几何方程给出的应变一定满足变形协调方程吗?为什么?
我所认识的应力和应变关系 在这之前我认识了应力和应变的概念、性质以及从静力学和几何学的角度出发所得到的平衡方程和几何方程。但是平衡方程仅反映了应力分量和外力分量的关系;几何方程仅建立了位移分量和应变分量的关系。 而谈到应力与应变的关系,对于可变形固体,在弹塑性力学中,在外力的作用下,其将发生变形。变形分为两个阶段,弹性阶段和塑性阶段。在弹性阶段,发生的弹性变形可以完全恢复,它是一个可逆过程。此时,应力与应变的关系是一一对应的,是单值函数关系。而在塑性阶段,所发生的塑性变形是不可以恢复的,是不可逆过程。相对应的,塑性阶段的应力应变的关系是非线性关系,不存在一一对应的关系。 我所认识的应力和应变的关系就是本构关系。本构关系也称为物理关系,它反应的是可变形材料的固有属性,实质上是一组联系力学参数和运动参数的方程式,也就是我们所说的本构方程。 在说应力与应变的关系之前,先说一下本构关系的相关影响因素,包括材料、环境、加载类型、以及加载速度。即,),,(T t f εσ=。另外,有各种各样的本构系,比如:弹性本构关系、塑性本构关系、粘弹性本构关系、粘塑性本构关系、各向同性本构关系、各向同性本构关系等等。 简单情况的本构关系: 应力和应变的关系包括弹性和塑性的应力应变关系。我们所说的是线性弹性体的应力应变关系,又分为简单应力状态和复杂应力状态。在简单拉伸情况下,理想弹性材料的应力和应变的关系很简单,就是材料力学中的胡克定律: 。 而在塑性阶段,应力应变之间不再是简单的胡克定律,而是 。 另外,简单拉伸情况下的卸载定律是 。在后继弹性阶段,也就是卸 载后重新加载的材料会继续发生新的塑性变形,在此时的屈服称为后继屈服,相应的屈服点称为后继屈服点。初始屈服和后继屈服的不同是:第一,应力的数值不一样,后继屈服的应力值更大;第二,屈服点的个数不一样。初始屈服点只有一个,而后继屈服点会有好多个,则其对应的应力值也会有很多个。最后,在卸载全部载荷后进行反向加载比如说把拉伸改成压缩,此时会产生Bauschinger 效应。对于该效应,说明材料在某一个方向的硬化将引起反方向的软化。也就是说,各向同性材料产生塑性变形之后会变成各向异性。此时的弹性阶段的卸载荷压缩 可表示: 。 总结一下材料弹塑性行为的特殊规律大致有以下三点:一是在弹性阶段应力应变的关系是线性的,在塑性阶段它们之间的关系是非线性的;二是应力应变在 εσE =)(εσΦ=εσ?=?E - +=s s σσ